Figure 1: The block diagram of Intelligent Vision Agent System.

Image

Information

Intelligent

Agent

Spatial 3D

Model

Vision

Information

Sensing

and

Control

Space, Object

and Camera

Constraints

Desired

Information

PLANNING OF A MULTI STEREO VISUAL SENSOR SYSTEM

FOR A HUMAN ACTIVITIES SPACE

Jiandan Chen, Siamak Khatibi and Wlodek Kulesza

The University of Kalmar, Norra Vagen 47, Kalmar, Sweden

Keywords: Sensor Placement, Multi Stereo View.

Abstract: The paper presents a method for planning the position of multiple stereo sensors in an indoor environment.

This is a component of an Intelligent Vision Agent System. We propose a new approach to optimize the

multiple stereo visual sensor configurations in 3D space in order to get efficient visibility for surveillance,

tracking and 3D reconstruction. The paper introduces a constraints method for modelling a Field of View in

spherical coordinates, a tetrahedron model for target objects, and a stereo view constraint for the baseline of

paired cameras. The constraints were analyzed and the minimum amount of stereo pairs necessary to cover

the entire target space was optimized by an integer linear programming. The 3D simulations for human

body and activities space coverage in Matlab illustrate the problem.

1 INTRODUCTION

Vision is one of the most important information

sources for humans. Human senses and the ability to

process this information may be extended by the use

of advanced technologies. The Intelligent Vision

Agent System, IVAS, is such a high-performance

autonomous distributed vision and information

processing system. It consists of multiple sensors for

gathering information and surveillance but also

control of these sensors including their deployment

and autonomous servo. It is able to extract 3D model

information from a real scene of target objects, and

compare this with a pattern in order to make

decisions. Meanwhile the patterns are also renewed

by the inclusion of a learning phase. These features

enable the system to dynamically adjust camera

configurations to track, recognize and analyze the

objects, to achieve the desired 3D information. The

Intelligent Agent consists of a knowledge database,

with learning and decision making components.

Figure 1 shows the block diagram working sequence

of the IVAS. The paper focuses on the planning of

stereo pair deployment of the system.

The critical problem for the system is to find the

optimal configuration of sensors so that the features

of the environment and target objects are visible

under the required constraints. The sensors’ intrinsic

and extrinsic parameters are examples of parameters

considered while choosing the configuration. The

system also requires optimal configuration for stereo

pair design.

1.1 Related Works

The sensor planning can be viewed as an extension

to the well-known Art Gallery Problem, AGP,

(O’Rourke, 1987). In its simplest form, the AGP

describes a simple polygon, often with holes, and the

task is to calculate the minimum number of guards

necessary to cover the entire polygon. Sensor

planning has a similar goal, to minimize the number

480

Chen J., Khatibi S. and Kulesza W. (2007).

PLANNING OF A MULTI STEREO VISUAL SENSOR SYSTEM FOR A HUMAN ACTIVITIES SPACE.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 480-485

 SciTePress

of sensors needed to cover the target space. The

AGP has a Field of View, FoV, of 360° for the

guards, whereas in sensor planning the camera’s

FoV is limited by image resolution and the viewable

angles of cameras. A stereo view requires the target

space to be covered by at least two views.

Camera placement algorithms based on binary

optimization techniques are known, and analyzed for

camera deployment in a polygonal space in 2D

space (Erdem&Sclaroff, 2006). Also a linear

programming method to optimize sensor placement,

with respect to coverage, has been developed

(Hörster&Lienhart, 2006; Chakrabarty et al., 2002).

Using the sensor detection range r to solve the area

of grid coverage problem is common (Hörster

&Lienhart, 2006; Chakrabarty et al., 2002; Zou

&Chakrabarty, 2004). A quality metric including a

probabilistic occlusion can be used to evaluate the

optimum configurations of multiple cameras (Chen,

2002). The sensor planning can be analyzed by

examining the visibility in the dynamical

environment, and the result simulated by re-

annealing software (Mittal, 2006). An optimal stereo

vision configuration for a mobile robot focuses on

optimizing the stereo pair orientation to detect static

obstacles where the stereo pair is assumed to be

known a priori (Huang&Krotkov, 1997). For a

model-based sensor placement, the target geometry

information is known (Fleishman et al., 2000;

Chen&Li, 2004). Mobile single camera positioning

to optimize the observability of human activity has

been studied (Bodor et al., 2005). There has been

relatively little work on determining optimal

multiple sensors for sensor configurations

(Mittal, 2006).

2 PROBLEM FORMULATION

The algorithm proposed in the paper works in 3D

space and a new approach to define the camera’s

FoV, applied in spherical coordinates, is proposed.

In the presented solution the maximum volume of

FoV coverage becomes a part of sphere that

simplifies the calculation. The definition is

intrinsically related to the sensor’s physical

parameters, such as the dimension of the CCD and

focus length. For the camera’s view, this paper

considers not only the problem of coverage, but also

the orientation of the target. To deal with this, a

target space is modelled by a tetrahedron. The

presented method formulates all factors into the

constraints, and has a flexible way to add other

constraints. Knowledge of stereo technology is

integrated, a greedy stereo pair search algorithm

solving for the minimal amount of stereo pairs by

Integer Linear Programming, ILP, is proposed and

the ILP model is given.

2.1 Problem Statement and Main

Contributions

The paper addresses the problem of determining the

optimum amount of cameras and corresponding

positions and poses to observe human body and

activities space in stereo views.

The main contributions of the paper may be

summarised as follow:

• The new approach to modelling a 3D FoV using

spherical coordinates;

• Modelling of human and target space as

tetrahedrons;

• Stereo pairs formulation by a greedy algorithm

using stereo constraints;

• Minimizing the amount of stereo pairs by means

of the stereo view integer linear programming

model.

2.2 Definitions and Constraints

The space denotes a 3D indoor environment. The

target object or space describes the space for human

body and activities, and is required to be covered by

cameras’ FoVs. In other words, it should be visible

to the cameras and respect the minimal requirements

of each constraint. The constraints analysis ensures

sufficient data of scene features for 3D

reconstruction and image analysis. Design of the

optimal parameters for cameras’ positions, poses and

stereo baseline length is done according to the

criteria from cameras’ FoVs; the target objects and

stereo matching.

The following factors formulate the constraints:

Field of View is the maximal space volume visible

from a camera. The FoV is a cone determined by the

azimuth and elevation within a spherical coordinate

system.

Image Resolution, IR, describes the visibility of the

object in a camera view as the size of the object in

the image. IR is affected by the distance from

camera to the target object and the angle between the

camera view direction and the orientation of the

target objects surface.

Stereo Baseline Length is the distance between the

paired cameras in a stereo view. Stereo matching

becomes harder when the baseline length increases.

PLANNING OF A MULTI STEREO VISUAL SENSOR SYSTEM FOR A HUMAN ACTIVITIES SPACE

481

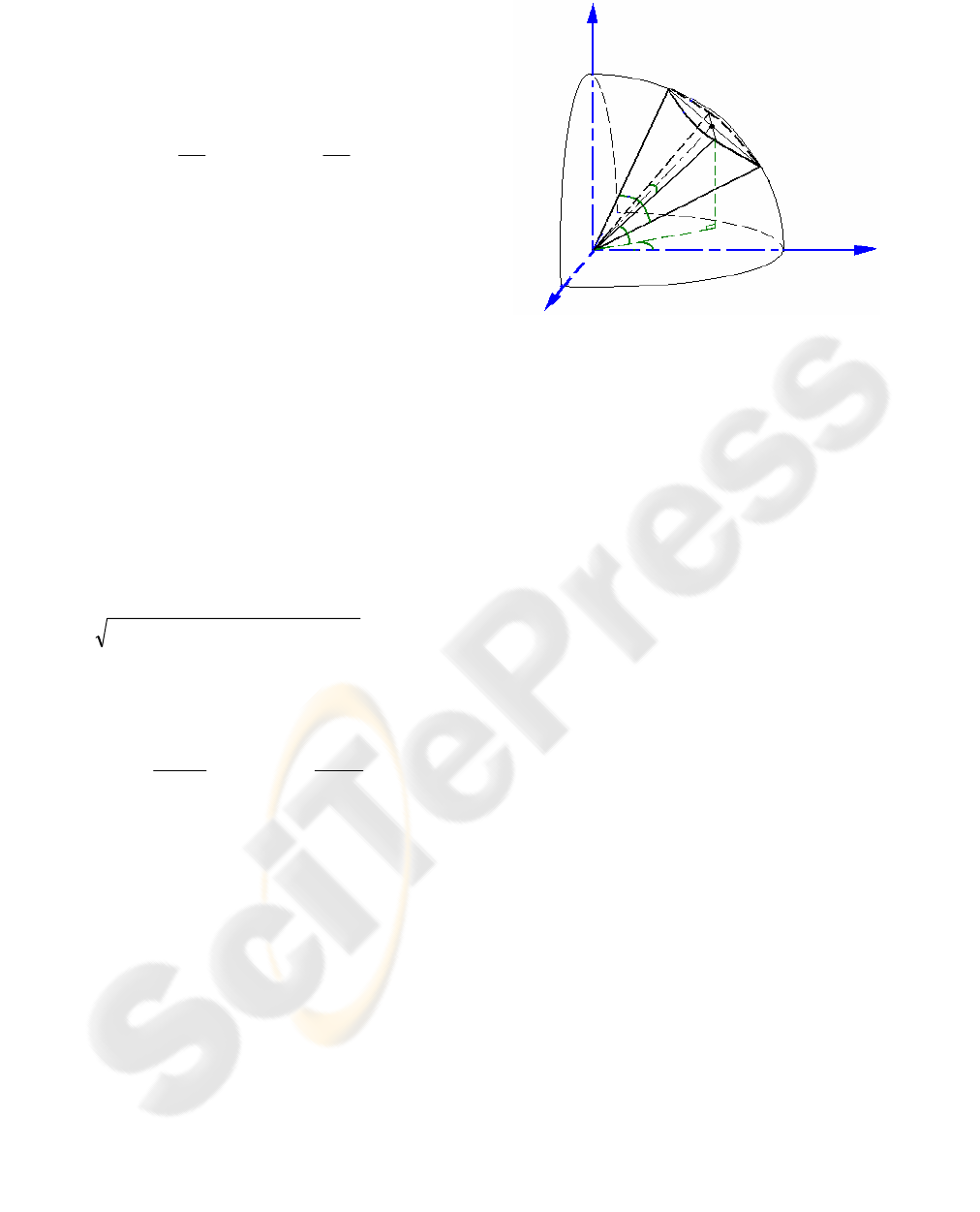
Figure 2: The spherical coordinates system and FoV of a

camera.

2.2.1 Camera Constraints

The horizontal and vertical viewable angles of the

camera can be determined by the focal length of the

lens and the size of the CCD element:

arctan2=

(1)

where

and

define the horizontal and vertical

viewable angles of the camera FoV; S

, S

are the

horizontal and vertical dimensions of the CCD

element, and f is the focal length of the lens.

The camera working distance, r, is the radius of

a sphere and can be calculated from the focal length

of the lens f and image resolution requirement.

The camera position C(x

) and pose

(

) describe the camera’s extrinsic parameters.

The camera pose defines its azimuth

and

elevation

In the world frame, the target object and

camera’s position and pose are described in

Cartesian coordinates. In the camera view, a

spherical coordinate system is applied. The distance

l between the target position O(x,y,z) and camera

position C(x

) is:

222

)()()(

ccc

zzyyxxl −+−+−=

(2)

The azimuth

and elevation

of target object

with respect to camera position are given by

−

= arctan

−

= arcsin

(3)

In order for the target object feature point to be

covered by the camera’s FoV, the following

constraints must be fulfilled:

rl ≤

and

2/2/

hcohc

+≤≤−

2/2/

vcovc

+≤≤−

(4)

In the spherical coordinate systems, the range of

the camera’s FoV is directly determined by

, S

and f, which makes it easy to dynamically compute

FoV according to the changing of the focal length

The modelling of the FoV can be viewed as a part of

the sphere, as shown in Figure 2.

2.2.2 Object Constraints

In the human living environment, we always have

some knowledge about the target objects and space

under observation, e.g. the floor plan of the room,

the geometric properties of the furniture, human

body and activities space, etc.

The 3D target object or space can be modelled

by a tetrahedron, giving four triangles. We define

four vertices of tetrahedron by

1,2,3,4

, as in

Figure 3. The three upward triangles are required to

be covered by cameras’ FoVs. The normal of each

triangle gives the orientation of the surface.

If the

visibility angle

, between the triangle normal n

and a line drawn from the centroid of triangle to

camera position increases then the image resolution

decreases. In order to get good image resolution, an

angle

less than the maximum visibility angle

max

is required:

max

≤

(5)

It is best that the camera orientation

lines up

with the centroid of triangle, bringing the target

object to the centre of the camera’s FoV and causing

less lens distortion. The angle between camera

orientation

and a line drawn from camera position

to the centroid of triangle less than the maximum

max

is also required and constrained as:

max

≤

(6)

The triangle is considered to be covered if all

three vertices are within a camera’s FoV and fulfil

constraints (5) and (6), guaranteeing good

observability of the target object.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

482

Figure 3: Illustration of the human space modelled as

tetrahedron;

- the visibility angle between triangle normal

and a line from the centroid of the triangle to camera

position;

- the angle between camera orientation c

and a

line from the camera position to centroid of the triangle.

2.2.3 Stereo Pair Constraints

We construct the stereo coverage from the overlap

of two cameras’ FoVs. Overlapping FoVs are

typically used in computer vision for the purpose of

extracting 3D information (Khan

et al., 2001). The

area of stereo coverage must cover all of the target

objects. Assuming the camera is a pinhole camera,

the 3D depth

is given by (Faugeras, 1993):

Z =

(7)

where

B is the baseline length between two cameras

and

dx is the disparity.

The accuracy of depth resolution relies on stereo

matching, but stereo matching becomes harder as the

baseline length increases. Hence, we have a

constraint defining the maximum baseline length for

stereo matching:

max

BB ≤

(8)

3 APPROACHES

The stereo pair placement problem consists of two

stages. Firstly, we find potential stereo pairs that

satisfy stereo constraint by greedy searching from all

potential cameras’ positions and poses. Secondly,

we minimize the amount of stereo pairs needed,

subject to the coverage constraint.

3.1 Greedy Algorithm

The algorithm gives a flexible way to organize

cameras into stereo pairs, each potential camera to

be included in a stereo pair may be chosen by an

algorithm according to the stereo pair constraint.

The first step of the algorithm is to sample the

potential camera’s positions

) and poses

(

) of the camera state, ,

Scamera

where

k is camera state index number. The target object,

which we must cover, is modelled as a tetrahedron.

In the next step, we compute all of the potential

cameras’ positions and poses needed to cover each

upward triangle of this model. Taking this, we

combine every two camera states to be a potential

stereo pair,

Stereopair

, according to the stereo

constraint (8). The algorithm is sufficiently flexible

to add other constraints for stereo pairs, e.g. the

angle constraint between the cameras’ optical axes.

Finally the algorithm removes the redundant

potential stereo pairs.

3.2 Stereo View Integer Linear

Programming Model

This model assumes that one type of camera is used

throughout, resulting in just one camera’s FoV being

considered. The optimization of the amount of

cameras with different FoVs also can be easily

extended, by adding one more term for different

FoVs. Since the stereo pairs have been found by the

greedy algorithm, the integer linear programming

can be applied to minimize the total stereo pairs

subject to the coverage constraint (Hörster

&Lienhart, 2006; Chakrabarty et al., 2002).

A binary variable is computed and stored in

advance. The stereo visibility binary variable table

Stereovis

j,i

is defined by:

otherwise

modelobject target of e triangl

covers a if

Stereopair

Stereovis

⎪

⎩

⎪

⎨

⎧

(9)

which indicates each triangle

j as the row j to be

covered by the stereo pair

i in the column i, and

≤

1 , where K

is the total number of stereo

pairs.

This objective function minimizes the number of

stereo pairs needed to cover all triangles in the target

object model, and also ensures that the target object

is covered by at least one stereo pair:

PLANNING OF A MULTI STEREO VISUAL SENSOR SYSTEM FOR A HUMAN ACTIVITIES SPACE

483

Figure 4: The human space modelled as tetrahedron with

corresponding cameras’ positions and poses changing

according to the model location; (a) perspective view (b)

top view (c) side view.

(

)

(

)

(

)

∑

min

(10)

subject to

≥×

∑

StereovisS

, 32,1,for =j

(11)

where the

is the binary variable where a “1”

indicates the stereo pair to be chosen.

To ensure that only one camera is located at

each position and has only one pose, the conflict

binary variable table

p,i

is also calculated in advance

and defined by:

for

i=1, 2,

…

, K

, and p=1, 2,

…

, K

One more constraint is added into the model:

≤×

∑

K,, p ,21 for ⋅⋅⋅=

(13)

The information on the optimal number of stereo

pairs, and which pairs to use, are returned as vectors

by the ILP model.

4 RESULTS

The described algorithm was simulated in MATLAB

7.0. The integer linear programs lpsove package

(Berkelaar et al., 2005) and the Epipolar Geometry

Toolbox (Mariottini&Prattichizzo, 2005) were used

to minimise the amount of cameras and transform

the object position in 3D separately. The simulation

environment considers a rectangular room with size

8x8x3 m. The modelling of the human body as a

tetrahedron requires three upward triangles; each of

them occludes the triangles behind it and must be

visible to at least one pair of cameras. The human

model is 2 m high and 1.2 m at the base edges. The

cameras’ positions are restricted to the ceiling

around the room, their potential positions sampled at

half meter intervals, and the poses sampled at 12°

intervals. The camera has same horizontal and

vertical viewable angles

of 60° and has a

working distance

of 7 m. The maximum visibility

angle

max

and the angle

max

are taken to be 70° and

10° respectively. The maximum stereo baseline

length B

max

is 1.5 m.

This case study illustrates the optimum amount

of stereo pairs with corresponding cameras’

positions and poses changing according to the model

location. In order to clearly show cameras’ positions

and poses, the analysis only considers the model at

otherwise

wherens, orientatio

different with camera same

theshare and pairs twoif

≠

⎪

⎩

⎪

⎨

⎧

(12)

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

484

three locations 1, 2 and 3, see Figure 4. The arrows

indicate the optical axes of the cameras. The index

numbers indicate the model locations and

corresponding cameras’ positions and poses. In each

position every upward triangle surface is visible to at

least one stereo pair; the algorithm proves that a set

of two pairs is sufficient to cover three triangle

surfaces. When the model moves from position 1 to

position 2, the stereo pair positions (0,200) and

(0,250) change to (0,0) and (0,50) respectively. The

elevation angle is increased as the model moves

further away from the camera. At the same time,

another stereo pair located at (600,0) and (650,0)

moves to (800,100) and (800,150) respectively, the

elevation angle is decreased as the model moves

closer to it. The azimuth

and elevation

stereo pair may vary by camera individually. Both

two stereo pairs follow the model when the model

changes from position 2 to position 3, see Figure 4.

5 CONCLUSION

The proposed approach is useful in determining the

optimal number of cameras and their corresponding

positions and poses to observe human body and

activities space in stereo view. The stereo pair has

the flexibility to adjust cameras’ poses and positions

individually. Multi camera planning and control for

surveillance and tracking in supermarkets, museums

and the home environment, and especially in

situations which require stereo data to reconstruct

3D, are possible fields of application.

To model the target object as a tetrahedron

gives a convenient way to extract the orientation of

each surface and guarantee a good observability.

Modelling camera’s FoV using spherical coordinates

simplifies the model and constraints, which speeds

up computations. Formulating the stereo pairs with

greedy algorithm using stereo constraints is a simple

way to get all possible stereo pairs and then

minimize the amount of stereo pairs by means of the

stereo view ILP model.

It is possible to extend this algorithm to

dynamic cameras to track humans. In order to follow

target objects movement, the camera movement

distance constraints can be applied (Chen et

al., 2007). The human activities space also can be

extended to a large space modelled by multiple

tetrahedrons. The space can be covered without

changes of cameras’ positions and poses. Future

work may focus on dynamic occlusions and tracking

multiple dynamic objects by using multiple dynamic

stereo pairs.

REFERENCES

Berkelaar, M., Notebaert, P., and Eikland, K., 2005,

Lpsolve 5.5: Open Source (mixed-integer) Linear

Programming System. Eindhoven Univ. of

Technology,

http://tech.groups.yahoo.com/group/lp_solve/files/.

Bodor, R., Drenner, A., Janssen, M., Schrater, P.,

Papanikolopoulos, N., 2005, Mobile Camera

Positioning to Optimize the Observability of Human

activity Recognition Task. Intelligent Robots and

Systems, IEEE/RSJ Int. Conf.

Chakrabarty, K., Iyengar, S. S. , Qi, H., and Cho., E.,

2002, Grid Coverage for Surveillance and Target

Location in Distributed Sensor Networks.

IEEE

Transaction on Computers

, 51(12): 1448-1453.

Chen, J., Khatibi, S., Kulesza, W., 2007, Planning of A

Multi Stereo Visual Sensor System Depth Accuracy

and Variable Baseline Approach. Submitted to

3DTV-

Conference

, Greece.

Chen, S. Y., Li Y. F., 2004, Automatic Sensor Placement

for Model-Based Robot Vision. IEEE Transactions on

Systems, Man, and Cybernetics VOL.34, No.1

Chen, X., 2002, Design of Many-Camera Tracking

Systems for Scalability and Efficient Resource

Allocation. PhD thesis, Stanford University.

Erdem, U., Sclaroff, S., 2006, Automated Camera Layout

to Satisfy Task-Specific and Floor Plan-Specific

Coverage Requirements. Computer Vision and Image

Understanding

103, 156-169.

Faugeras, O., 1993,

Three-dimensional computer vision.

MIT Press.

Fleishman, S., Cohen-Or, D., and Lischinski, D., 2000,

Automatic Camera Placement for Image-based

modelling. Computer Graphics Forum, 19(2):101-110.

Huang, W. H. , Krotkov, E. P., 1997,

Optimal Stereo

Mast Configuration for Mobile Robots.

Processing of

IEEE Int. Conf. Robotics.

Hörster, E., Lienhart, R., 2006, On the Optimal Placement

of Multiple Visual Sensors,

ACM International

Workshop on Video Surveillance & Sensor Networks

Khan, S., Javed, O., Rasheed, Z., Shah, M., 2001, Human

Tracking in Multiple Cameras. The Eighth IEEE Int.

Conf. On Computer Vision.

Mariottini, G. L., Prattichizzo, D., 2005, The Epipolar

Geometry Toolbox: Multiple View Geometry and

Visual Servoing for Matlab

. Robotics and

Automation,Proceedings of the IEEE Int. Conf

Mittal, A., 2006, Generalized Multi-Sensor Planning

. 9th

European Conference on Computer Vision (ECCV).

O’Rourke, J.,1987

Art Gallery Theorems and Algorithms.

Oxford University Press.

Zou, Y. and Chakrabarty, K., 2004, Sensor Deployment

and Target Localization in Distributed Sensor

Network. Trans. On Embedded Computing Sys.,

3(1):61-91.

PLANNING OF A MULTI STEREO VISUAL SENSOR SYSTEM FOR A HUMAN ACTIVITIES SPACE

485