IMAGE BASED STEGANOGRAPHY AND CRYPTOGRAPHY
Domenico Bloisi and Luca Iocchi
Dipartimento di Informatica e Sistemistica
Sapienza University of Rome, Italy
Keywords:
Steganography, cryptography.
Abstract:
In this paper we describe a method for integrating together cryptography and steganography through image
processing. In particular, we present a system able to perform steganography and cryptography at the same
time using images as cover objects for steganography and as keys for cryptography. We will show such system
is an effective steganographic one (making a comparison with the well known F5 algorithm) and is also a
theoretically unbreakable cryptographic one (demonstrating its equivalence to the Vernam Cipher).
1 INTRODUCTION
Cryptography and steganography are well known and
widely used techniques that manipulate information
(messages) in order to cipher or hide their existence.
These techniques have many applications in computer
science and other related fields: they are used to pro-
tect e-mail messages, credit card information, corpo-
rate data, etc.
More specifically, steganography
1
is the art and
science of communicating in a way which hides the
existence of the communication (Johnson and Jajodia,
1998). A steganographic system thus embeds hid-
den content in unremarkable cover media so as not to
arouse an eavesdropper’s suspicion (Provos and Hon-
eyman, 2003). As an example, it is possible to embed
a text inside an image or an audio file.
On the other hand, cryptography is the study of
mathematical techniques related to aspects of infor-
mation security such as confidentiality, data integrity,
entity authentication, and data origin authentication
(Menezes et al., 1996). In this paper we will focus
only on confidentiality, i.e., the service used to keep
the content of information from all but those autho-
rized to have it.
Cryptography protects information by transform-
ing it into an unreadable format. It is useful to achieve
1
from Greek, it literally means ”covered writing”
confidential transmission over a public network. The
original text, or plaintext, is converted into a coded
equivalent called ciphertext via an encryption algo-
rithm. Only those who possess a secret key can deci-
pher (decrypt) the ciphertext into plaintext.
Cryptography systems can be broadly classified
into symmetric-key systems (see Fig. 1) that use a
single key (i.e., a password) that both the sender and
the receiver have, and public-key systems that use two
keys, a public key known to everyone and a private
key that only the recipient of messages uses. In the
rest of this paper, we will discuss only symmetric-key
systems.
Figure 1: Symmetric-key Cryptographic Model.
Cryptography and steganography are cousins in
the spy craft family: the former scrambles a mes-
sage so it cannot be understood, the latter hides the
127
Bloisi D. and Iocchi L. (2007).
MAGE BASED STEGANOGRAPHY AND CRYPTOGRAPHY.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 127-134
Copyright
c
 SciTePress

message so it cannot be seen. A cipher message,
for instance, might arouse suspicion on the part of
the recipient while an invisible message created with
steganographic methods will not.
In fact, steganography can be useful when the
use of cryptography is forbidden: where cryptogra-
phy and strong encryption are outlawed, steganog-
raphy can circumvent such policies to pass message
covertly. However, steganography and cryptography
differ in the way they are evaluated: steganography
fails when the ”enemy” is able to access the content
of the cipher message, while cryptography fails when
the ”enemy” detects that there is a secret message
present in the steganographic medium (Johnson and
Jajodia, 1998).
The disciplines that study techniques for decipher-
ing cipher messages and detecting hide messages are
called cryptanalysis and steganalysis. The former de-
notes the set of methods for obtaining the meaning
of encrypted information, while the latter is the art of
discovering covert messages.
The aim of this paper is to describe a method for
integrating together cryptography and steganography
through image processing. In particular, we present a
system able to perform steganography and cryptogra-
phy at the same time. We will show such system is an
effective steganographic one (making a comparison
with the well known F5 algorithm (Westfeld, 2001))
and is also a theoretically unbreakable cryptographic
one (we will demonstrate our system is equivalent to
the Vernam cipher (Menezes et al., 1996)).
2 IMAGE BASED
STEGANOGRAPHIC SYSTEMS
The majority of today’s steganographic systems uses
images as cover media because people often transmit
digital pictures over email and other Internet commu-
nication (e.g., eBay). Moreover, after digitalization,
images contain the so-called quantization noise which
provides space to embed data (Westfeld and Pfitz-
mann, 1999). In this article, we will concentrate only
on images as carrier media.
The modern formulation of steganography is of-
ten given in terms of the prisoners’ problem (Sim-
mons, 1984; Kharrazi et al., 2004) where Alice and
Bob are two inmates who wish to communicate in or-
der to hatch an escape plan. However, all commu-
nication between them is examined by the warden,
Wendy, who will put them in solitary confinement at
the slightest suspicion of covert communication.
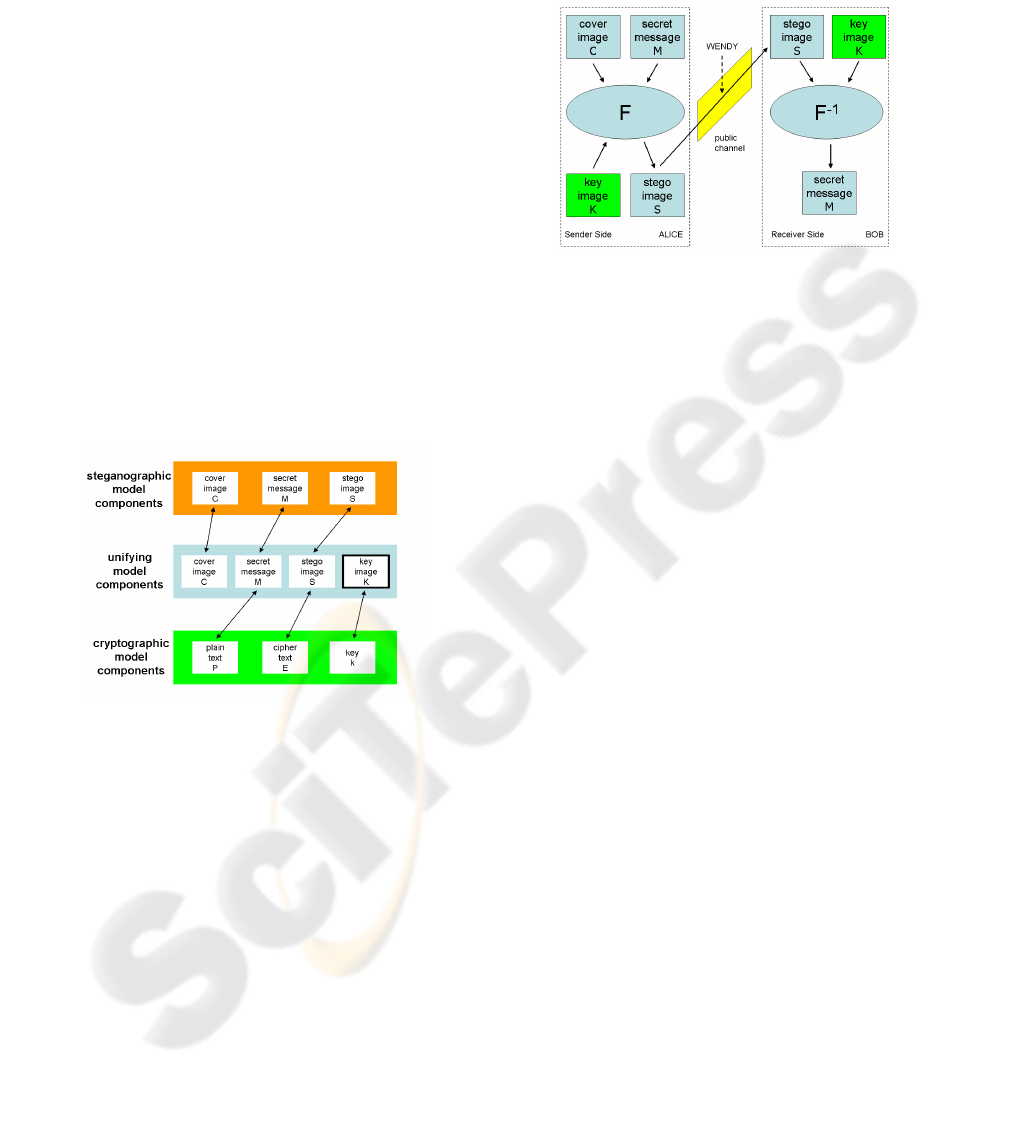
Specifically, in the general model for steganogra-
phy (see Fig. 2), we have Alice (the sender) wishing
to send a secret message M to Bob (the receiver): in
order to do this, Alice chooses a cover image C.
The steganographic algorithm identifies C’s re-
dundant bits (i.e., those that can be modified with-
out arising Wendy’s suspicion), then the embedding
process creates a stego image S by replacing these re-
dundant bits with data from M.
Figure 2: Steganographic Model.
S is transmitted over a public channel (monitored
by Wendy) and is received by Bob only if Wendy has
no suspicion on it. Once Bob recovers S, he can get
M through the extracting process.
The embedding process represents the critical task
for a steganographic system since S must be as simi-
lar as possible to C for avoiding Wendy’s intervention
(Wendy acts for the eavesdropper).
Least significant bit (LSB) insertion is a common
and simple approach to embed information in a cover
file: it overwrites the LSB of a pixel with an M’s bit. If
we choose a 24-bit image as cover, we can store 3 bits
in each pixel. To the human eye, the resulting stego
image will look identical to the cover image (Johnson
and Jajodia, 1998).
Unfortunately, modifying the cover image
changes its statistical properties, so eavesdroppers
can detect the distortions in the resulting stego im-
age’s statistical properties. In fact, the embedding of
high-entropy data (often due to encryption) changes
the histogram of colour frequencies in a predictable
way (Provos and Honeyman, 2003; Westfeld and
Pfitzmann, 1999).
Westfeld (Westfeld, 2001) proposed F5, an algo-
rithm that does not overwrite LSB and preserves the
stego image’s statistical properties (see Sect. 5.2).
Since standard steganographic systems do not pro-
vide strong message encryption, they recommend to
encrypt M before embedding. Because of this, we
have always to deal with a two-steps protocol: first
we must cipher M (obtaining M’) and then we can
embed M’ in C.
In the next sections we will present a new all-in-
one method able to perform steganography providing
VISAPP 2007 - International Conference on Computer Vision Theory and Applications
128

strong encryption at the same time.
Our method has been planned either to work with
bit streams scattered over multiple images (in an on-
line way of functioning) or to work with still images;
it yields random outputs, in order to make steganaly-
sis more difficult and it can cipher M in a theoretically
secure manner preserving the stego image’s statistical
properties.
The simplicity of our method gives the possibility
of using it in real-time applications such as mobile
video communication.
3 A STEGO-CRYPTOGRAPHIC
MODEL
Figures 1 and 2 depict the cryptographic and stegano-
graphic system components. Here we discuss how we
could unify those two models, in order to devise a
new model holding the features that are peculiar both
to the steganographic and to the cryptographic model
(see Fig. 3).
Figure 3: Mapping between model components.
The mapping between P and M, E and S, and k and
K is possible because we can consider all the compo-
nents in Fig. 3 as bit sequences and then realize a
relation between the co-respective bit sets.
The unifying model results as a steganographic
one with the addition of a new element: the key image
K. It gives the unifying model the cryptographic func-
tionality we are searching for, preserving its stegano-
graphic nature.
The unifying model embedding process yields S
exploiting not only C’s bits but also K’s ones (see
Sect. 4.1): this way of proceeding gives Alice the
chance to embed the secret message M (that is, the
plaintext) into the cover image C (as every common
steganographic system) encrypting M by the key im-
age K (as a classical cryptographic system) at the
same time. At the receiver side, Bob will be able to
recover M through S and K (see Sect. 4.2). In addi-
tion, Wendy will neither detect that M is embedded in
S nor be able to access the content of the secret mes-
sage (see Fig. 4).
Figure 4: The unifying model.
4 IMAGE BASED
STEGANOGRAPHY AND
CRYPTOGRAPHY
The function denoted by F in Fig. 4 represents
the embedding function we are going to explain in
this section. The symbol F
−1
indicates the ex-
traction function, since it is conceptually the in-
verse of embedding. We will call ISC (Image-
based Steganography and Cryptography) the algo-
rithm which carries on such functions.
4.1 ISC Embedding Process
Figure 5 shows the embedding process. The choice
of the stego image format makes a very big impact on
the design of a secure steganographic system.
Raw, uncompressed formats, such as BMP, pro-
vide the biggest space for secure steganography, but
their obvious redundancy would arise Wendy’s suspi-
cion (in fact, why someone would have to transmit big
uncompressed files when he can strongly reduce their
size through compression? (Fridrich et al., 2002)).
Thus, ISC embedding algorithm must yield a com-
pressed stego image, in particular we choose to pro-
duce a JPEG file, because it is the most widespread
image format.
While the output of the embedding process is a
JPEG image (as we noted above), the inputs are: the
secret message bit sequence, an image C, and an im-
age K. C and K can be either uncompressed images
(e.g., BMP) or compressed ones (e.g., JPEG), in ad-
dition they can be either distinct images or the same
image.
IMAGE BASED STEGANOGRAPHY AND CRYPTOGRAPHY
129

Stereo Image Pair). In fact, the key image idea de-
rives from stereo vision: if you imagine the extracting
process is a correlation algorithm, the secret message
M could be seen as a disparity map between S and K,
the embedding process as a sort of inverse correlation.
5 ISC PERFORMANCE
In this section we will present ISC performance with
respect to both steganography and cryptography. We
first demonstrate that ISC has optimum cryptographic
performance, by proving that it is equivalent to Ver-
nam cipher (Menezes et al., 1996), and then compare
ISC steganographic performance with respect to the
well known F5 algorithm (Westfeld, 2001).
5.1 ISC Cryptographic Performance
The Vernam Cipher. The Vernam cipher is a
symmetric-key cipher defined on the alphabet A =
{0, 1}. A binary message m
1
, m
2
, ..., m
t
is operated on
by a binary key string k
1
, k
2
, ..., k
t
of the same length
to produce a ciphertext string c
1
, c
2
, ..., c
t
where c
i
=
m
i
⊕ k
i
, for 1 ≤ i ≤ t and ⊕ is the XOR operator.
The ciphertext is turned back into plaintext simply in-
verting the previous procedure, i.e., m
i
= c
i
⊕ k
i
, for
1 ≤ i ≤ t.
If the key string is randomly chosen and never
used again, the Vernam cipher is called a one-time
pad.
One-time pad is theoretically unbreakable: if a
cryptanalyst has a ciphertext string c
1
, c
2
, ..., c
t
en-
crypted using a random key string which as been
used only once, the cryptanalyst can do no better then
guess at the plaintext being any binary string of length
t. To realize an unbreakable system requires a ran-
dom key of the same length as the message (Shannon,
1949).
Equivalence between Vernam Cipher and ISC.
Let keyAC[] and coverAC[] be two arrays contain-
ing the AC nonzero coefficients extracted from the
key image K and the cover image C respectively.
Let stegoAC[] be an array initialized identical to
coverAC[] (stegoAC[] will be modified during the
embedding process because it will store the change
needed by coverAC[]).
Let M[] be a binary array containing all the
bits from the secret message M and let us suppose,
for the sake of simplicity, that length(keyAC[]) =
length(coverAC[]) = length(M[]). We want to find the
following one-way relations RK, RS, and RM:
keyAC[]
RK
−−→ k
1
, k
2
, ..., k
t
stegoAC[]
RS
−→ c
1
, c
2
, ..., c
t
M[]
RM
−−→ m
1
, m
2
, ..., m
t
The last relation RM is simply the relation of
equivalence since both M[] and m
1
, m
2
, ..., m
t
are bit
sequences.
For finding RK we have to transform keyAC[] in
a bit sequence through two further relations RK1 and
RK2:
keyAC[]
RK1
−−→ keyEO[]
RK2
−−→ k
1
, k
2
, ..., k
t
RK1 maps each AC coefficient keyAC[i] over a bi-
nary alphabet and store the corresponding bit value in
keyEO[i] trough the rule:
if keyAC[i] is even
keyEO[i] = 0
else
keyEO[i] = 1.
end if
RK2 is the relation of equivalence between
KeyEO[] and k
1
, k
2
, ..., k
t
. RK results as the combi-
nation of RK1 and RK2.
We can repeat the above procedure for finding RS
as a combination of RS1 and RS2, i.e.,
stegoAC[]
RS1
−−→ stegoEO[]
RS2
−−→ c
1
, c
2
, ..., c
t
Let us use RS1 on coverAC[] in order to obtain
coverEO[] identical to stegoEO[] (note that initially
stegoAC[] is equal to coverAC[]).
coverAC[]
RS1
−−→ coverEO[]
Now we transform Em1 in order to work with bit
sequences, obtaining the algorithm Em2:
Embedding Algorithm Em2.
Input: coverEO[], keyEO[], M[]
Output: stegoEO[]
for every bit M[i] of the binary array M[]
if (M[i] == 1)
if (coverEO[i] ⊕ keyEO[i] == 0) (1)
stegoEO[i] = coverEO[i] ⊕ 1 (2)
end if
end if
else //M[i] = 0
if (coverEO[i] ⊕ keyEO[i] == 1) (3)
stegoEO[i] = coverEO[i] ⊕ 1 (4)
end if
end else
end for
IMAGE BASED STEGANOGRAPHY AND CRYPTOGRAPHY
131

Lines 1,2,3, and 4 perform (in the binary domain)
the same operations made by algorithm Em1. Table 1
shows the truth table for every input feasible by algo-
rithm Em2.
Table 1: Truth table for algorithm Em2.
M[i] keyEO[i] coverEO[i] stegoEO[i]
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 0
You can notice that bold values correspond to the
truth table for c
i
= m
i
⊕ k
i
. Since M[] corresponds to
the Vernam plaintext m
1
, m
2
, ..., m
t
(by virtue of RM),
keyAC[] corresponds to the Vernam key k
1
, k
2
, ..., k
t
(by virtue of RK1 and RK2), and stegoAC[] corre-
sponds to the Vernam ciphertext c
1
, c
2
, ..., c
t
(by virtue
of RS1 and RS2) we can conclude asserting:
ISC embedding process and Vernam cipher en-
crypting step are equal.
The proof of equivalence between ISC extracting
process and Vernam cipher decrypting step is trivial.
Let us transform algorithm Ex1 in order to work
with M[], keyEO[], and stegoEO[].
Algorithm Ex2.
Input: stegoEO[], keyEO[]
Output: keyEO[]
for every bit stegoEO[i] of stegoEO[]
M[i] = stegoEO[i] ⊕ keyEO[i]
end for
Since Ex2 is identical to the Vernam cipher de-
crypting step (m
i
= c
i
⊕k
i
, for 1 ≤ i ≤ t), we have that
ISC extracting process and Vernam cipher decrypting
step are equal.
Eventually, ISC and Vernam cipher are equivalent.
5.2 ISC Steganographic Performance
The ISC steganographic performance will be mea-
sured by comparing it with the well known F5 algo-
rithm (Westfeld, 2001). In order to do this, we will
compare the statistical behaviour of these two algo-
rithms on the same input set. This will demonstrate
that ISC withstands both visual and statistical attacks
(Westfeld and Pfitzmann, 1999): visual attacks mean
that one can see steganographic messages on the low
bit planes of an image because they overwrite visual
structures; statistical attacks consist in measure dis-
tortions in the DCT coefficients’ frequency histogram
produced by embedding.
F5 Algorithm. The F5 steganographic algorithm
was introduced by Andreas Westfeld in 2001 (West-
feld, 2001). The goal of his research was to de-
velop concepts and a practical embedding method for
JPEG images that would provide high steganographic
capacity without sacrificing security (Fridrich et al.,
2002).
Instead of replacing the least-significant bit of a
DCT coefficient with message data, F5 decrements
its absolute value in a process called matrix encod-
ing. As a result, there is no coupling of any fixed
pair of DCT coefficients, meaning the χ
2
-test (Provos
and Honeyman, 2003; Westfeld and Pfitzmann, 1999)
cannot detect F5 (χ
2
-test measure the probability a
DCT coefficients’ frequency histogram is the product
of a steganographic process).
F5 uses a permutative straddling mechanism to
scatter the message over the whole cover medium.
The permutation depends on a key derived from a
password.
Moreover, F5 (as ISC) embeds data in JPEG im-
ages thus resulting immune against visual attacks be-
cause it operates in a transform space (i.e., the fre-
quency domain) and not in a spatial domain.
Comparison between F5 and ISC. In order to re-
alize a meaningful comparison between ISC and F5
2
,
we must embed the same message m into the same
cover image c using both ISC and F5. After embed-
ding, we have two stego images: S
F5
produced by F5
and S
ISC
generated by ISC. Both S
F5
and S
ISC
present
a DCT coefficients histogram different from the c’s
original one. What we are interested in is to com-
pare the amount of modifications introduced by F5
and ISC.
Figure 7 shows the result of such comparison ob-
tained using a JPEG cover set C
set
of 20 images (1024
x 768, average size 330 KB). In every image of C
set
we have embedded a canto from Dante’s Divina Com-
media (about 5 KB for each canto) with a JPEG qual-
ity factor set to 80. Only for ISC, we also used the
images of C
set
as key images.
The mean difference (in percentage) for every AC
coefficient in the interval [−8, 8] is shown on the y-
axis in Fig. 7, in particular the black columns rep-
resent the differences introduced by F5 embedding
step while the white ones correspond to the number
2
release 11+
VISAPP 2007 - International Conference on Computer Vision Theory and Applications
132