A DISTRIBUTED VISION SYSTEM FOR BOAT TRAFFIC

MONITORING IN THE VENICE GRAND CANAL

D. Bloisi, L. Iocchi, G. R. Leone, R. Pigliacampo

Dip. di Informatica e Sistemistica, University of Rome ”La Sapienza”, via Salaria 113, Rome, Italy

L. Tombolini

ECOTEMA-Ingegneria per l’Ambiente srl, Cannaregio 463, Venice, Italy

L. Novelli

Archimedes, via Tagliamento 9, Rome, Italy

Keywords:

Motion detection and Tracking, Distribuited surveillance, Boat trafﬁc monitoring.

Abstract:

In this paper we describe a system for boat trafﬁc monitoring that has been realized for analyzing and com-

puting statistics of traﬁc in the Grand Canal in Venice. The system is based on a set of survey cells to monitor

about 6 Km of canal. Each survey cell contains three cameras oriented in three directions and covering about

250-300 meters of the canal. This paper presents the segmentation and tracking phases that are used to detect

and track boats in the channel and experimental evaluation of the system showing the effectiveness of the

approach in the required tasks.

1 INTRODUCTION

Wave motion has been recognized as one of the ma-

jor causes of damage to the basement structures of

historical buildings in Venice since the early 1960’s,

with the increase in boat mass and speed consequent

to the diffusion of large diesel engines. Since then, the

Venetian Municipal Authorities have been involved

in deﬁning rules and tradeoffs suitable for the need

of mobility of goods, inhabitants and tourists on one

hand, and the need of preservation of historical her-

itage on the other hand. Measures such as speed limits

and strict trafﬁc behavior rules, though, were proven

to be only partly effective, due to the lack of continu-

ous and autonomous trafﬁc monitoring systems.

In the 1990’s the public water-bus ﬂeet was

equipped with GPS satellite receivers and a ﬁrst rough

speed and trajectory monitoring system was put in

place. In the years 2004-2005 a modern wide-range

general ﬂeet control system (SALOMON) was built

up. The major feature of this system is the ability of

the on-board equipment to deﬁne an extremely accu-

rate boat position while holding a complete map of the

city waterways with their related speed limits; in this

way, the speed detected by the on-board Differential

GPS receiver is immediately compared with the rele-

vant speed limit and a signal is immediately issued to

the boat driver in case of infringement. SALOMON

system was proven to be very effective and precise;

however, because of the need of a permanent install-

ment of the intelligent navigation unit on the boats,

its use is currently limited to the major resident ﬂeets

only.

In early 2006, the Municipal Administration

launched the ARGOS project (Automatic Remote

Grand Canal Observation System) for boat trafﬁc

monitoring, measurement and management along the

Grand Canal of Venice based on automated vision

techniques. This new system will answer to the spe-

ciﬁc requirements for the boat navigation rules in

Venice while providing a combined uniﬁed view of

the whole Grand Canal waterway. Such features far

exceed the performance of any commercially avail-

able product. Therefore, a speciﬁc software has to

be developed, based on the integration of advanced

automated image analysis techniques. The ARGOS

system will provide a uniﬁed man-machine interface

both for the data detected through automatic vision

and the ones detected by the former GPS-based sys-

tems. In turn, the precise GPS positioning data pro-

duced by the boats equipped with SALOMON naviga-

tion units will be used for ARGOS cameras automatic

549

Bloisi D., Iocchi L., R. Leone G., Pigliacampo R., Tombolini L. and Novelli L. (2007).

A DISTRIBUTED VISION SYSTEM FOR BOAT TRAFFIC MONITORING IN THE VENICE GRAND CANAL.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 549-556

 SciTePress

geometric calibration.

In this paper we describe the implementation of

the computer vision based system that allows for de-

tecting and tracking the boats in the canal. After a

brief overview of the ARGOS project given in Sec-

tion 2, we will describe Segmentation and Tracking

processes in Sections 3 and 4. Section 5 describes

some applications of the described modules and ex-

perimental evaluation of the system performance.

2 PROJECT OVERVIEW

The ARGOS system is going to control a waterway of

about 6 km length, 80 to 150 meters width, through

some observation posts (Survey Cells). The system

is based on the use of groups of IR/VIS cameras, in-

stalled just below the roof of several buildings lean-

ing over the Grand Canal (a ﬁrst prototype of a sur-

vey cell is visible in Figure 1) . Detected images

will be rectiﬁed and stitched together so as to gen-

erate a composite plain view, similar to a radar im-

age. Each survey cell is composed of 3 optical sen-

sors: one center wide-angle (90 degree), orthogonal

to the navigation axis, and two side deep-ﬁeld cam-

eras (50-60 degree). The resulting overall view ﬁeld

along the waterway could stretch over 250-300 me-

ters end-to-end. The three cameras are connected to a

Figure 1: The survey cells are installed on the top of several

buildings leaning over the Grand Canal.

local computer where images are processed through

a two-level analysis software: a module for image

re-sampling, rectiﬁcation and stitching of contiguous

images which, in turn, feeds a second software layer

capable of detecting moving targets, delimiting them,

ﬁnding their geometrical center and ﬁltering the time

and position data by means of tracking algorithms to

compute position, speed and direction of each tar-

get. The ﬁelds of view of each camera shall slightly

overlap so as to allow the software to continuously

follow and track the motion of each target through

the whole composite view ﬁeld of the survey cell,

keeping each target labelled by a unique identiﬁer

(Track ID). Each survey cell is also equipped with a

pan-tilt-zoom (PTZ) camera, for the automatic high-

resolution tracking of selected targets. Due to the im-

possibility of wiring the survey cells together, all the

system data trafﬁc shall be conveyed through a private

radio channel. As this channel has a limited band-

width, most of the computation load shall be borne by

the survey cells themselves. The system has to be de-

signed for 24/7 all-weather day-night operation. The

global system architecture is depicted in Figure 2.

Figure 2: All the system data trafﬁc shall be conveyed

trough a private radio channel.

The main ARGOS functions are: 1) Optical de-

tection and tracking of moving targets present in the

FOV; 2) Computing position, speed and heading of

any moving target within the FOV of each camera;

3) Elaboration at survey cell level of any event (tar-

get appears, exits, stops, starts within the cells FOV)

and transmission of any event to the Control Cen-

ter; 4) Connecting all the track segments related to

the same target in the different cameras FOV into a

unique trajectory and track ID; 5) Recording all the

video frames together with the graphical information

related to track IDs and trajectories; 6) Rectifying all

the camera frames and stitching them into a compos-

ite plain image so as to show a plan view of the whole

Grand Canal; 7) Allowing the operator to graphically

select any target detected by the system and automat-

ically activating the nearest PTZ camera to track the

selected target.

In order to achieve ARGOS objectives we de-

signed and developed a computer vision software

which is a pipeline of image analysis and tracking

techniques: we apply background subtraction and op-

tical ﬂow to the streams coming from the cameras to

obtain observations (i.e., to detect the part of the im-

age where the boats are); this information (position,

dimension, versus, and velocity of a boat) is used by

a set of Kalman Filters to track the targets over time.

The next two sections explain our approach in de-

tails.

3 SEGMENTATION

Our goal is to detect the moving targets in the sce-

nario (the boats): given a frame sequence from a

ﬁxed camera, we have to detect the zones of the

images representing all the objects that are passing

through. A common and effective technique to do

that is called background subtraction. The back-

ground image is not ﬁxed but must adapt to: grad-

ual illumination changes and sudden ones (such as

clouds), motion changes (camera oscillations), high

frequency background objects (waves in our case),

changes in the background geometry (such as parked

boats). A simple way to build the background is to

assign to a pixel the mean of all correspective ones

in a set of images. But this method does not work

well with illumination changes. Different methods

for background modelling, updating and subtraction

have been proposed. Two classiﬁcation directions

can be identiﬁed: how the background is modeled,

how the model is updated. Statistical models have

been widely used: either in the form of single Gaus-

sians (Wren et al., 1997; Jabri et al., 2000) or mix-

ture of Gaussians (Stauffer and Grimson, 2000; El-

gammal et al., 2000), but also other models (median

(Cucchiara et al., 2003), minimum-maximum values

(Haritaoglu et al., 2000), etc.) proved effective. The

choice of the model mostly depends on the kind of

scenario in which the application runs.

In our case single Gaussian models are not ade-

quate because we deal with outdoor environment with

ﬂuctuating background. This means that the distrib-

ution concerning a certain pixel often has more than

one peak. So our approach is based on a mixture of

Gaussians. The system computes the bar chart for

every pixel (i.e., the approximation of the distribu-

tion) in the RGB color space and it clusters the raw

data in sets based on distance in the color space. In

order to save computational time, only the two bigger

clusters are considered. If cardinality of the clusters

are comparable, both the values are recorded, other-

wise only the dominant one is considered. This solu-

tion allows for balancing efﬁciency with the need of

representing ﬂuctuations in the background.

When two boats are very near it is common to

have an error called under segmentation due to the

perspective of the camera view: the foreground im-

age has only one bigger blob instead of two or more.

To improve the detection in this situation we consider

also the optical ﬂow which correlates two consecu-

tive frames. Every feature which is present in both

the frames has a motion vector (direction,versus and

value) which is not null if the position in the two

frames is different. Optical ﬂow is a good approxi-

mation of the motion over time in image coordinates.

The system considers two directions for the central

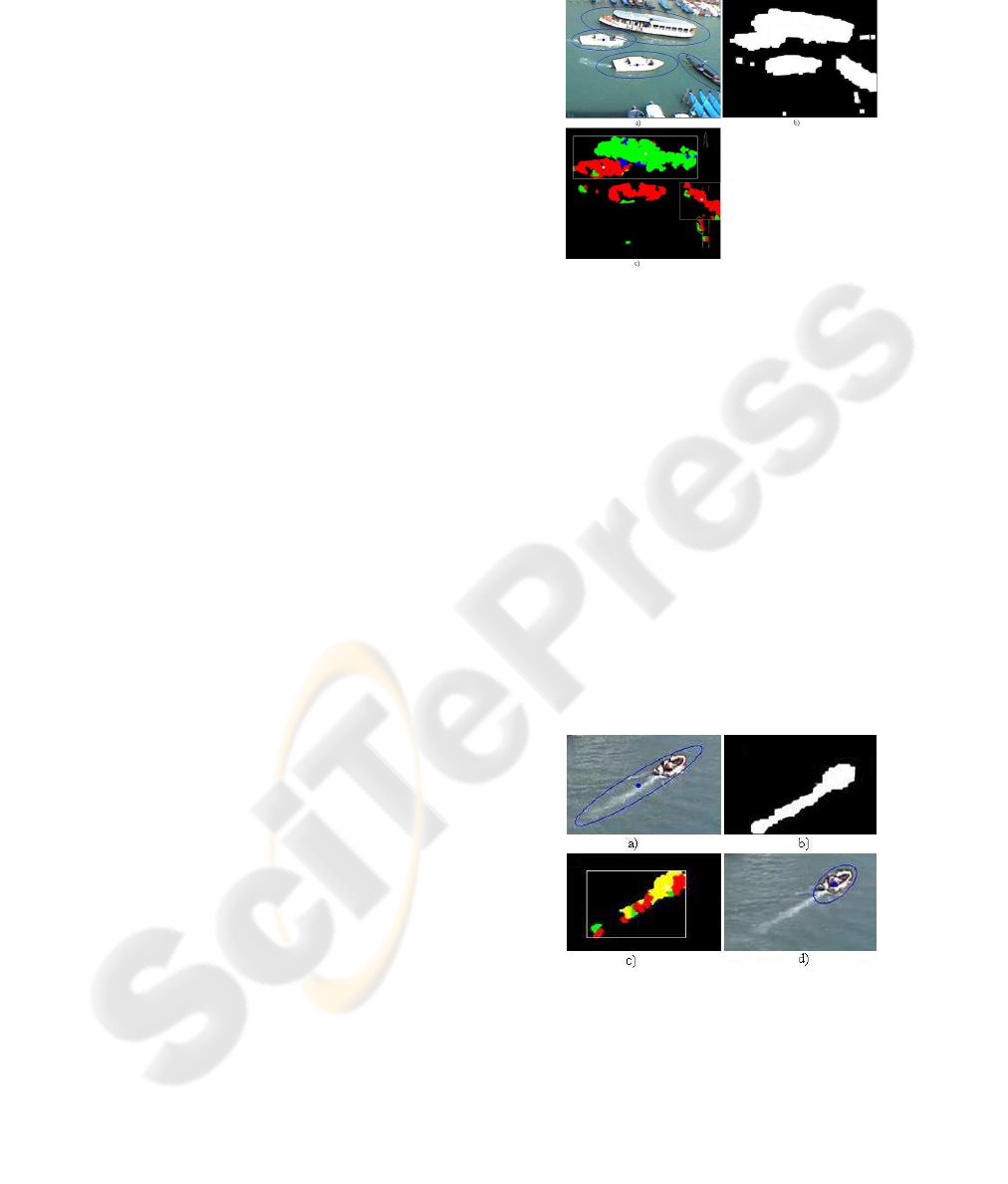
Figure 3: An example of under-segmentation: a) there are

four boats in the scene but b) the system detects three blobs.

c) Using optical ﬂow the system understands the different

directions of the boats and a) gives correct ellipses detec-

tions.

camera (left to right and right to left) and four di-

rections for the left and right cameras (because the

perspective is not orthogonal) A typical example of

under-segmentation correctly solved with optical ﬂow

is showed in Figure 3. Optical ﬂow is often useful

also when we have a single boat with a long wake on

the back. Figure 4-b shows another typical segmen-

tation error: the dimension of the boat is estimated

more than double than the real one. Using optical

ﬂow (Figure 4-c) the system detects a big yellow blob

that corresponds to the boat and other little ones in

different directions which are the water waves. Also

in this case optical ﬂow provides a correct detection

(Figure 4-d)

Figure 4: Example of wrong segmentation caused by water

waves: b) The blob in the foreground image is much bigger

than the real boat and a) the system gives a wrong detection

result but c) using optical ﬂow the system distinguishes the

boat from the waves and d) we obtain the correct detection.

However, this approach fails when a boat is in-

volved in particular maneuvers. For example, when

a boat turns around itself, the optical ﬂow may detect

different directions for the different parts of the boat

(e.g., one for the prow and another for the stern) and

discard (for some frames) detection of such a target.

Moreover, it is not useful when boats travel close by

in the same direction. From an analysis of the per-

formance of the segmentation process on many live

video streams from our application scenario, we have

evaluated that situations where optical ﬂow worsen

the performance of the segmentation process are very

limited, with respect to the advantages in reﬁning seg-

mentation when two boats moving in different direc-

tions come close and in presence of long waves after

the tracked boat. In summary, the algorithm used for

image segmentation consists of the following steps:

Background formation: a set S of n frames is used to

build the background image B which represents only

the static (i.e. non-moving) part of the scenario. This

procedure is done continuously to adapt to the sce-

nario’s changes. Foreground computation: the dif-

ference between the current image I from the camera

and the B image of the background gives the fore-

ground image F. This image is a binary image and

contains only elements which are not in the back-

ground (new elements in the scenario); an example is

Figure 3-b). Blob formation: the binary image B is

analyzed in order to ﬁnd connected components (i.e.,

blobs). Optical ﬂow reﬁning: for every detected blob

optical ﬂow is computed. If there is only one domi-

nant moving direction (more than 70%) the blob is

conﬁrmed, otherwise the blob is split in the different

directions detected. In addition, optical ﬂow is used

to eliminate wave noise. Ellipse approximation: el-

lipses calculated on the size of the blobs represent an

approximation of the boats detected. The centroids of

the ellipses are used to track the boats over time (see

Section 4).

4 MULTI-HYPOTHESIS KALMAN

FILTER TRACKING

An optimal recursive data processing algorithm for

tracking moving targets over time is the Kalman Fil-

ter (Welch and Bishop, 2004; Maybeck, 1979). Such

a ﬁlter represents an efﬁcient solution to the gen-

eral problem of estimating the state of a discrete-time

controlled process. When developing a multi-object

tracking method, one usually has to deal with track

initiation, track update including prediction and data

association and track deletion. The process is di-

vided into two fundamental steps: association: as-

signment of each incoming observation to a speciﬁc

target track; estimate: the receivedobservationis used

to provide a state estimate of the associated track.

Each time a new observation is received, it must be

associated to the correct track among the set of the

existing tracks, or, if it represents a new target, a

new track must be created. Thus, the tracking sys-

tem needs some mechanisms of Data Association and

tracks management (see (Hall and Llinas, 2001)).

This is a single hypothesis approach which means that

at all times an observation is associated to only one

of the existing tracks. If a wrong association hap-

pens (i.e. an observation is associated to a wrong

track) the system cannot recover from this error. In

our case, especially when we have a very crowded

scene, it is not straightforward to assign an observa-

tion to a certain track. For this reason we use a multi-

hypothesis Kalman ﬁlter tracking system. Every time

there is an observation that could be assigned to more

than one track the system considers the two hypothe-

ses for every candidate track (i.e. every track is di-

vided in two new ones). This is called track split.

This technique leads to the proliferation of the num-

ber of tracks and we need to detect and delete redun-

dant track (track merging. In the next paragraph we

illustrate with more details the single and multi hy-

pothesis tracking phases.

4.1 Single Hypothesis Tracking

4.1.1 Data Association

The technique used for the data association is the

Nearest Neighbor rule. When a new observation is

received, all existing tracks are projected forward to

the time of the new measurement. Then the observa-

tion is assigned to the nearest such estimate.

More generally, the distance calculation is computed

to reﬂect the relative uncertainties (covariances) as-

sociated with each track and observation. The most

widely used measure of the correlation between two

mean and covariance pair {x

} and {x

which are assumed to be Gaussian-distributed random

variables, is:

ass

) =

exp(−

− x

)(P

+ P

)

−1

− x

)

2π | (P

+ P

) |

(1)

If this quantity is above a given threshold, the two

estimates are considered to be feasibly correlated.

An observation is assigned to the track with which

it has the highest association ranking. In this way, a

multiple-target problem can be decomposed into a set

of single-target problems.

4.1.2 Track Formation

The nearest-neighbor rule is very simple and intu-

itive, but presents some difﬁculties. A ﬁrst problem is

in creating initial tracks for multiple targets, because

some components of the vector state are not directly

measurable. In the case of a single target, two ob-

servations can be accumulated to derive an estimate

of such components. For multiple target, there is no

obvious way to deduce such initial values: the ﬁrst

two observations could represent successive position

of a single object or the initial detection of two dis-

tinct objects. Every subsequent observation could be

the continuation of a known track or the start of a new

one.

So when a new observation is obtained, if it is not

highly correlated with an existing track, a new track is

created and a new Kalman ﬁlter is initialized with the

position (x,y) observed and given to all the not ob-

served components (e.g., velocity) a null value with

a relatively high covariance. If the subsequent ob-

servations conﬁrm the track existence, the ﬁlter will

converge to the real state.

4.1.3 Track Deletion

In many cases, some objects are not observed for a

while, with the uncertainty in the state estimate in-

creasing. Moreover the presence of noisy sensors can

determine spurious observations, which give rise to

spurious tracks. Thus, the tracking system needs an

additional mechanism to recognize and delete tracks

that do not receive any subsequent conﬁrming obser-

vations.

We have considered, as indicative measure of the un-

certainty in the state estimate of each target, the ﬁlter’

s gain relative to the track:

= P

−

(HP

−

+ R)

−1

(2)

and experimentally established a threshold for the

track deletion: if the received observations do not

conﬁrm a certain track for a period of time, the gain

value grows exceeding the threshold and the track is

deleted.

4.2 Multi Hypothesis Tracking

4.2.1 Track Splitting

When two objects are sufﬁciently close together, the

observations are highly correlated with more than one

track. In these cases a misassignment can cause the

Kalman-ﬁltering process to converge very slowly, or

fail to converge altogether. Moreover, tracks updated

with misassigned observations (or not updated at all)

will tend to correlate poorly with subsequent obser-

vations and may, therefore, be mistaken as spurious

by the track deletion mechanism; mistakenly deleted

tracks then necessitate subsequent track initiation and

a possible repetition of the process.

The choice of a multi-hypothesis tracking has been

made to give a solution to the problem of assignment

ambiguity: when the correct association is not

known, more association hypothesis are created. The

new observation received is used to update all the

tracks with which it has a probability association

that exceeds the threshold value. A copy of the not

updated track is also maintained (track splitting).

Subsequent observations can be used to determine

which assignment is correct.

4.2.2 Track Merging

One important issue of the track splitting technique

is a proliferation in the number of tracks. Because

track splitting does not decompose multiple-target

tracking into independent single-target problems, the

deletion mechanism described in section 4.1.3 is not

sufﬁcient. For example, two hypothesis tracks may

lock onto the trajectory of a single object; because

both tracks are valid, the standard track-deletion

mechanism cannot eliminate either of them.

The deletion procedure has to be modiﬁed to detect

redundant tracks and, therefore, cannot look at just

one track at a time. At each step, for each track

the correlation with all the other tracks is calculated

using equation (1). If the association probability be-

tween two tracks exceeds a threshold (experimentally

established), one of the two tracks is deleted, keeping

only the most signiﬁcant hypothesis.

Figure 5: a)Two boats very near are detected as one be-

cause there is a b)Foreground under segmentation error and

c)Optical ﬂow does not solve the problem but d)With the

multi-hypothesis method the system continues to track the

boats separated over time.

A successful example of this tracking method is

shown in Figure 5: when two boats are very near

they are detected as one (ellipse in Figure 5-a) be-

cause there is a foreground under segmentation error

(Figure 5-b) and also the optical ﬂow does not solve

the problem because the boats go in the same direc-

tion(Figure 5-c). Thanks to the multi-hypothesis ap-

proach the system considers the wrong observation

as a new track but it continues to track over time

the former two because of the history of the obser-

vations(Figure 5-d).

5 APPLICATION AND RESULTS

In order to make available all the information gath-

ered by the system in a useful way for the Venice Mu-

nicipal Authorities, we have developed different visu-

alizations of the results of the system.

The main control windowshowsa live global view

of the Grand Canal, integrating a GIS map with live

information about position and velocity of the boats

currently in the canal (see Figure 6). More speciﬁ-

cally, we plot a colored dot in the current map location

of each target with associated a few smaller dots rep-

resenting its recent track. The color denotes the speed

of the vehicle and other icons may appear close by to

indicate speciﬁc events (such as, moving in a wrong

way, stopping in a forbidden area, etc.) In addition,

ﬂow and density analysis are performed and displayed

in order to have a global view of the trafﬁc present in

the canal at every time (example in Figure 7).

Figure 6: The main control window shows a live global

view of the Grand Canal with live information about po-

sition and velocity of the boats currently in the canal.

The relevant information that must be extracted to

achieve the functionalities described above can be di-

vided in two groups: statistics measures and event de-

tection.

The ﬁrst kind of information is necessary to con-

tinuously monitor the trafﬁc in the Canal. In particu-

lar, we want to calculate the trafﬁc of boats moving in

each direction for each survey-cell at different times

of the day, as well as the boat density in the differ-

ent areas of the Canal. To this end track analysis has

been performed in order to compute the quantities of

interest. For example, for computing the ﬂow of boats

passing within the area monitored by a survey cell we

can deﬁne two virtual lines in the Canal and count the

number of boats (i.e., tracks) passing these lines.

Figure 7: Density analysis are performed and displayed in

order to have a global view of the trafﬁc present in the canal

at every time.

Another important measure is the velocity of the

boats, since this is the main cause of wave motion

that has been recognized as one of the major causes of

damage to the basement structures of historical build-

ings in Venice. The velocity is computed by analysis

of the world coordinates of the tracks: in particular to

increase robustness to noise we compute the length of

the path done in the last n frames (e.g., n = 10) as the

sum of the distances between consecutive points and

divide this value for the time duration of the path.

As for event detection, the main situations that

must be automatically detected are: speed limits, i.e.,

detecting boats going at a velocity greater than a given

threshold; parallel travel, i.e., detecting boats that

move parallel and close each other for long time

;

wrong directions, i.e., detecting boats moving in the

wrong direction in one-way pieces of the Canal; for-

bidden stops, i.e., detecting boats stopping in forbid-

den areas.

Event detection is again based on speciﬁc analysis

of the determined tracks. Speed limit is checked using

two thresholds (that have been ﬁxed to 5 Km/h and 7

Km/h) and each target is labeled with a color: green

for speed below 5 Km/h, yellow for speed between

5 and 7 Km/h and red for speed above 7 Km/h. The

visualization of colored dots in the GIS map makes

it possible to quickly detect speed limit violations.

Moreover, the system automatically records the tracks

moving at a velocity above 7 Km/h for some time, al-

lowing for subsequent analysis and post-processing.

Parallel travel is detected by track analysis, in which

we ﬁrst detect parallel motion (by projecting the po-

sition of one boat to the direction line of the other)

and then computing the distance between the two di-

rection lines. A pair of parallel boats that maintain

this distance below a given threshold for more than a

This is currently forbidden by Municipal Authorities.

given amount of time will generate an automatic alert.

Also in this case automatic recording will allow sub-

sequent analysis. Finally, the other eventsare detected

by deﬁning zones in the canal that activate the corre-

sponding checking procedures: for wrong direction

we simply check that boats move in the right direc-

tion, for stops detection we monitor the time in which

a boat remains within a limited area.

5.1 Performance Evaluation

The performance results reported here refer to the ca-

pability of the system to provide accurate trafﬁc sta-

tistics and event detection. It is important to notice

that, although one goal of the project is to achievebest

performance in associating a single track to each boat

(i.e., avoiding track splitting) for its entire presence

in the monitored area, statistics and events described

above do not strictly require such a property. It is in-

deed sufﬁcient that the boat is continuously tracked

over short periods of time. Consequently, the follow-

ing evaluation tests have been performed to measure

the performance of the system in counting and short-

term tracking of passing boats.

All the tests have been executed with the same

conﬁguration of the software (i.e., with no speciﬁc

optimization for a given functionality) on real images

taken from a survey cell installed in Venice. The tests

have been executed on long sequences of recorded

videos that have been taken at the same frame rate

of the software (about 5 fps).

Counting evaluation test. The ﬁrst evaluation test

has been set as follows. A virtual line has been put

across the Canal in the ﬁeld of view of a survey

cell, the number of boats passing this line has been

counted automatically by the system ˆn, and the same

value is manually calculated by visually inspection

n, the average percentage error is then computed as

ε = | ˆn− n|/n. This error measures the general perfor-

mance of the system, and it is useful to determine the

general capabilities of the system of estimating trafﬁc

ﬂow. However, this measure does not capture exactly

all the errors made by the system. For example, if a

boat is counted twice and another one is not detected,

the error ε is zero. An additional error measure is then

calculated by considering the probability of making

an error in counting a single boat passing the line

P(e) =

∑

t=0

δ(

− f

)

where δ(·) is 0 when the argument is 0 and 1 other-

wise.

This experiment has been performed with three

different videos of about 20 minutes each taken in dif-

ferent days. The results are shown in Table 1.

Table 1: Counting errors.

duration n ˆn ε P(e)

Video 1 32 min 90 95 0.055 0.144

Video 2 30 min 69 72 0.043 0.130

Video 3 25 min 62 67 0.081 0.129

Short-term tracking evaluation test . This test has

been performed in order to evaluate the ability of the

system to correctly perform short-term tracking, i.e.

to maintain the same identiﬁer to each target within a

limited amount of time. To this end we have deﬁned

two passing lines in different places in the canal and

measured the consistency of the tracks. More specif-

ically, we denote with n the number of boats passing

through the two lines and with c the number of boats

that have the same id between the ﬁrst and the second

line. Thus c/n represents the accuracy in short-term

tracking. We repeated the experiment several times

with different situations (single boat, two boats going

in the same direction and two boats going in opposite

direction). The results are shown in Table 2.

Table 2: Short-term tracking accuracy.

accuracy

Single boat 0.88

2 boats same dir. 0.75

2 boats opp. dir. 0.72

In addition to the quantitative test above, we have

performed qualitative tests. The live rectiﬁcation of

the perspective images in an integrated view (see Fig-

ure 6) allows to visually monitor all the area dedi-

cated to a survey cell. The display of dots associated

to tracked boats on top of the live rectiﬁed image al-

lows for a comprehensive and augmented view that

has proven to be very useful to the operators in the

Municipal Control Center. Finally, automatic regis-

tration of events and image storage and retrieval facil-

ities allows for subsequent analysis and for effective

monitoring of the canal.

6 CONCLUSION

In this paper we have presented an implemented sys-

tem for distributed monitoring and analysis of boat

trafﬁc in the Grand Canal of Venice. The system

is mainly based on two processes: segmentation and

tracking that computes tracks associated to the boats

moving in the waterway. The characteristics of these

processing modules are: robust and efﬁcient segmen-

tation that uses up to two Gaussians for modelling

the background and optical ﬂow to reduce segmenta-

tion errors; multi-hypothesis tracker based on Nearest

Neighbors data association and Kalman ﬁlters.

The system has proven to be effective in perform-

ing the tasks of monitoring and trafﬁc analysis, as re-

ported by experimental results. Additional evaluation

will be performed in order to provide additional ex-

perimental evidence of the performance of the system

as well as to improve its performance.

ACKNOWLEDGEMENTS

The project has been realized thanks to the view of the

future and to the active participation of the City Coun-

cil of Venice. In particular, special thanks to Lord

Vice-Major of Venice, On. Michele Vianello, for his

foresight in applying innovative technologies in the

delicate and complex historical city as Venice. We

are also grateful to the Responsible Manager Arch.

Manuele Medoro and his staff for their constant sup-

port and commitment.

REFERENCES

Cucchiara, R., Grana, C., Piccardi, M., and Prati, A. (2003).

Detecting moving objects, ghosts, and shadows in

video streams. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 25(10):1337–1342.

Elgammal, A. M., Harwood, D., and Davis, L. S. (2000).

Non-parametric model for background subtraction. In

Proc. of the 6th European Conference on Computer

(ECCV), pages 751–767, London, UK. Springer-

Verlag.

Hall, D. L. and Llinas, J. (2001). Handbook for multisensor

data fusion (Electrical engineering and applied signal

processing). CRC Press LLC.

Haritaoglu, I., Harwood, D., and Davis, L. S. (2000). W4:

Real-time surveillance of people and their activities.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 22(8).

Jabri, S., Duric, Z., Wechsler, H., and Rosenfeld, A. (2000).

Detection and location of people in video images us-

ing adaptive fusion of color and edge information.

In Proc. of 15th International Conference on Pattern

Recognition (ICPR’00), 4:4627.

Maybeck, P. S. (1979). Stochastic models, estimation and

control. vol I. ACADEMIC PRESS.

Stauffer, C. and Grimson, W. E. L. (2000). Learning

patterns of activity using real-time tracking. IEEE

Trans. on Pattern Analysis and Machine Intelligence,

22(8):747–757.

Welch, G. and Bishop, G. (2004). An introduction to the

kalman ﬁlter. Technical report, University of North

Carolina at Chapel Hill, NC 27599-3175.

Wren, C. R., Azarbayejani, A., Darrell, T., and Pentland,

A. (1997). Pﬁnder: Real-time tracking of the human

body. IEEE Trans. on Pattern Analysis and Machine

Intelligence, 19(7):780–785.