
AN APPROXIMATE REASONING TECHNIQUE FOR
SEGMENTATION ON COMPRESSED MPEG VIDEO
Luis Rodriguez-Benitez
Escuela Universitaria Politecnica, Universidad de Castilla-La Mancha, Almaden, Ciudad Real, Spain
Juan Moreno-Garcia
Escuela de Ingeniera Tecnica Industrial, Universidad de Castilla-La Mancha, Toledo, Spain
Javier Albusac, Jose Jesus Castro-Schez, Luis Jimenez
Escuela Superior de Informatica, Universidad de Castilla-La Mancha Ciudad Real, Spain
Keywords:
Segmentation and Grouping, Motion and Tracking, Approximate Reasoning, MPEG compressed domain.
Abstract:
In this work we present a system that describes linguistically the position of an object in motion in each frame
of a video stream. This description is obtained directly from MPEG motion vectors by using the theory of
fuzzy sets and approximate reasoning. The lack of information and noisy data over the compressed domain
justifies the use of fuzzy logic. Besides, the use of linguistic labels is necessary since the system’s output
is a semantic description of trajectories and positions. Several methods of extraction of motion information
from MPEG motion vectors can be found in the revised literature. As no numerical results are given of these
methods, we present a statistical study of the input motion information and compare the output of the system
depending on the selected extraction technique. For system performance evaluation it would be necessary
to determine the error between the semantic output and the desired object’s description. This comparison is
carried out between the (x,y) pixel coordinates of the center position of the object and the resulting value of a
defuzzification method applied to the description labels. The system has been evaluated using three different
video samples of the standard datasets provided by several PETS (Performance Evaluation of Tracking and
Surveillance) workshops.
1 INTRODUCTION
The work on MPEG compressed domain focused
mainly on video segmentation and camera motion de-
tection. (Antani et al., 2001) establish a use of motion
information to detect cuts (shot changes), activity in
a scene, camera motion parameters (pans, zooms,...),
etc. Some methods use only as input the motion infor-
mation stored in the motion vectors but another ones
like (Rapantzidos and Zervakis, 2005) combines the
motion information with DCT terms. Usually these
techniques are based on the construction and analysis
of a motion histogram. The use of approximate rea-
soning techniques such as fuzzy sets (Zadeh, 1960)
can be justified by the lack of information and the im-
precision inherently present on the compressed data.
For example, in (Yoon et al., 2000) the absence of
information is derived from the size of the search
window used to establish a correspondence of mac-
roblocks between adjacent frames. Fast movements
can not be detected as it occurs in sports. The impre-
cision is derived from the macroblock size of 16 x 16
pixels. If there exists almost two blobs smaller than
the macroblock size the encoded motion vector is not
capable of representing this motion in a right way. In
this paper we present an approach to the video seg-
mentation of objects motion in a sequence of images
coded as an MPEG video stream and it is organized
as follows: In the second section we present the struc-
ture of the MPEG stream, a short state of art of the
extraction methods of motion information and a com-
parison between them. Third section deals with some
basic concepts related to fuzzy sets, the construction
methodology of linguistic labels and the fuzzifica-
tion process to obtain a ”linguistic sequence”. The
fourth section analyses the intraframe segmentation
task based on a Euclidean distance and an aggrega-
tion algorithm and fifth section examines the semi-
automatic process of interframe segmentation to es-
tablish a correspondence of objects between frames.
184
Rodriguez-Benitez L., Moreno-Garcia J., Albusac J., Jesus Castro-Schez J. and Jimenez L. (2007).
AN APPROXIMATE REASONING TECHNIQUE FOR SEGMENTATION ON COMPRESSED MPEG VIDEO.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 184-191
Copyright
c
SciTePress

Finally we summarize our experiments in section 6,
followed by conclusion in section 7.
2 MOTION INFORMATION IN
MPEG CODED DATA
This section begins with the description of the kind
of frames stored in the MPEG stream and how the
motion information is represented through the motion
vectors. We continue with a review of different ap-
proaches to the extraction and interpretation of this
motion information. As in this review no numerical
comparison between extraction methods was found,
we finish this section showing results of statistical
tests to know the amount and quality of data obtained.
2.1 Structure of the Mpeg Stream
The MPEG stream is composed of three types of
frames, I, P and B. The Intracoded (I) encodes the
whole image, P and B, as it is shown in figure 1, are
coded using motion-compensation prediction from a
previous P or I frame, in the case of P, and from a
previous and future frame as reference, in the case of
B.
Figure 1: Reference frames in an mpeg stream.
The motion information in an MPEG stream video
is stored in the Motion Vectors (MVs). The Mac-
roblock is the basic unit in the MPEG stream and it
is an area of 16 by 16 pixels and within this the mo-
tion vectors are stored. In a video sequence there are
usually only small movements from frame to frame
and for this reason, the macroblocks can be compared
between frames, and as it is shown in figure 2 instead
of encoding the whole macroblock, the difference be-
tween the two macroblocks is encoded. The displace-
ment between two macroblocks in different frames
gives the motion vector associated with some mac-
roblock. A vector defines a distance and a direction
and has two components: right
x and down x.
The displacement of the motion vector is from
the reference frame and generally in applications like
(Pilu, 2001), focused on estimation of camera motion,
it is valid using these magnitudes but in another ones,
like video segmentation, to improve the reliability of
the system it is necessary to know the motion from
Figure 2: Motion vectors associated with one macroblock.
one frame to the next. As it is shown in figure 3 the
problem is that although P and B frames are supposed
to carry motion information, not all their blocks do.
So, in these cases, it is not possible to obtain this data
and as we describe in section 2.2 to resolve this prob-
lem approximation values must be used.
Figure 3: Real motion information.
2.2 Mpeg Information Extraction
In this paper the authors consider two main groups of
methods for extracting motion information, those who
calculate real displacement values from one frame to
the next and another group who approximate these
values to supply the lack of information, to simplify
the extraction process or to remove the inherent noise
of motion vectors. On the other hand, as will be seen
later, these methods could use only information re-
lated to a subset of frames depending of their type.
Some examples of extraction of approximate values
are like (Venkatesh et al., 2001) that uses a normal-
ization process by multiplying MVs from P and B
frames by 3 or -3 respectively. (Kim et al., 2002) di-
vide the magnitude of the motion vector between k,
with k the number of frames displaced from the refer-
ence frame. (Ardizzone et al., 1999) do not consider
the individual values of each motion vector but de-
scribes a prototypal motion vector field by subdivid-
ing the whole image into N quadrants and characteriz-
ing each of them with a parameter who represents the
average values of the magnitude and the direction of
all the motion vectors associated to macroblocks who
belongs to each quadrant. In (Venkatesh and Ramakr-
ishnan, 2002) are described two steps to remove noise
of motion vectors (i) Motion Accumulation (ii) Se-
lection of representative motion vectors. The motion
accumulation consist on a scale of the MVs to make

them independent of the frame type, a rounded to
nearest integer and establish an association between
the MV and the center pixel of the macroblock. The
sign of the backward MVs is reversed after the nor-
malization stage. The determination of representative
MVs is obtained by taking the median value of all
MVs corresponding to the same macroblock region.
In this work we calculate the real values of displace-
ment from all the P and B frames as is described in
(Gilvarry, 1999). In (Pilu, 2001) the authors consider
backward vectors very noisy and do not take them into
account and in many other justifies the use of only P
motion vectors because of computational efficiency.
Next, we present numerical results to differenti-
ate between selection based on data obtained from
P frames, B frames or both. The test video samples
are obtained from PETS data-sets (IEEE International
Workshop on Performance Evaluation of Tracking
and Surveillance). Environmentproperties, character-
istics of objects in motion, lighting conditions, cam-
era situation, ... are very different in each of the three
test videos. The trajectories of objects described by
our system are illustrated An image with partial tra-
jectory are shown from figure 8 to 10.
In the second column of the table 1 is shown the
percentage of macroblocks without motion vectors
associated for each one of the videos. The opposite
percentage is shown in the third and fourth columns
where there are the percentages of macroblockswhich
cannot and can be used to calculate the motion from
frame to next as seen in (Gilvarry, 1999) (motion vec-
tors in macroblocks of adjacent frames must be dif-
ferent than zero) respectively. The fourth column rep-
resents the set of input data values of our system
that is about a four percent of the total number of
macroblocks which could calculates displacement be-
tween frames. This is why previously was referred
an important absence of motion information, motion
vectors, in MPEG compressed domain.
Table 1: Macroblocks with motion information.
Video Without Non Calc. Calculable
1 86.5% 4.3% 9.2%
2 92.2% 3.4% 4.4%
3 95.5% 1.8% 2.7%
Average 93.5% 2.7% 3.9%
In table 2, a division of the motion vectors in for-
ward predicted and backward predicted is shown. The
percentage of forward nearly doubles backward but as
we present in table 3 this percentage is practically the
same if it is considered only motion vectors which al-
low to calculate motion from frame to next (column
fourth of table 1.
Table 2: Motion vectors by prediction direction.
Video Forward Backward
1 71.6% 28.4%
2 64% 36%
3 64.8% 35.2%
Average 66.8% 33.2%
Table 3: Prediction direction with computable motion.
Video Forward Backward
1 53.6% 46.4%
2 53% 47%
3 52.8% 47.2%
Average 53.1% 46.9%
3 HIGH LEVEL CONCEPTUAL
COMPONENTS
The aim of this work is to obtain a linguistic descrip-
tion of the position and motion direction of different
kinds of objectives by means of direct fuzzification of
motion vectors to obtain a high-levelconceptual char-
acterization called Linguistic Motion Vector. In this
section we start defining basic concepts of theory of
fuzzy sets which will be used as basis to construct and
define the linguistic motion vector and all the other
linguistic elements the system’s performance is based
in.
3.1 Linguistic Variables
A set of linguistic labels (Zadeh, 1975) SA
j
is defined
for each one of the input linguistic variables X
j
. The
set SA
j
is represented as:
SA
j
= {SA
1
j
, SA
2
j
, ..., SA
i
j
j
} (1)
where i is the position of the label SA
i
j
in the set
SA
j
, j is the number of the input linguistic variable
for the one that SA
j
is defined, and i
j
is the number of
linguistic labels in SA
j
.
For this work, the membership functions of lin-
guistic labels associated with the correspondingfuzzy
sets are shown from figure 4 to 7. As it can be ob-
served these sets of linguistic variables are always
continuous.
3.2 Linguistic Intervals
A linguistic interval (Moreno-Garcia et al., 2004)
of length c is a set of consecutive pairs of linguis-
tic labels defined in SA
j
and its membership function
value. It is represented as:
LI
c
j, p
= {[SA
p
j
, µ
SA
p
j
], . . . , [SA
p+(c−1)
j
, µ
SA
p+(c−1)
j
]} (2)

Figure 4: Linguistic variable horizontal velocity (hv).
Figure 5: Linguistic variable vertical velocity (vv).
where p is the position in SA
j
of the first linguistic
label of the linguistic interval and c is the number of
labels in the linguistic interval.
For instance, let us suppose that the set of linguis-
tic labels SA
j
is defined over the linguistic variable of
the figure Horizontal Position (figure 7). A possible
linguistic interval of length 2 LI
2
hp,2
is the set of lin-
guistic labels {[Left,0.8], [Centre Horizontal,0.2]} .
3.3 Linguistic Motion Vectors
A linguistic motion vector (Rodriguez-Benitez et al.,
2005) is a quintuple
LMV =< NumberFrame, LI
hv
, LI
vv
, LI
vp
, LI
hp
> (3)
where the first element denotes the number of the
frame the motion vector belongs to and the other four
elements are linguistic intervals obtained as the result
of fuzzification (Dubois and H.Prade, 1980) of the
data showed in table 4. The two first data sources are
obtained from the components of the motion vector
while the second one are obtained from the number-
ing of the macroblock associated with the motion vec-
tor. Each macroblock is identified by a number from 0
to a given value
n-1
, where
n
represents the total num-
ber of macroblocks in each frame. With n, the number
of macroblock and the total number of columns and
rows of the image, we can obtain the row and the col-
umn of the frame where the macroblock is situated.
A LMV represents a linguistic description of the
motion of a macroblock between consecutive frames.
An example is showed in table 5 where the vertical
position of the macroblock is between
very Up and
Up
and the horizontal position is between
Right and
Figure 6: Linguistic variable vertical position (vp).
Figure 7: Linguistic variable horizontal position (hp).
Very Right
, the horizontal motion is
Fast Left
and
there is no vertical motion (
No Motion
)
A linguistic motion vector is valid if it contains
information about the direction and velocity of an ob-
ject, i.e. at least one of the two magnitudes of the
LMV is distinct of the label ”No Motion”
In the example in the table 5 these components are
represented by the linguistic intervals LI
hv
and LI
vv
respectively.
LI
hv
: [Fast Left, 1];
LI
vv
: [No Motion, 1];
LI
hv
gives information about the horizontal dis-
placement of a possible object, so we can consider
this LMV as a Valid Linguistic Motion Vector
(VLMV).
3.4 Linguistic Object
The goal of this paper is to generate a linguistic de-
scription that characterizes the position and motion
trajectory of an object. A Linguistic Object (LO) al-
lows to represent this semantic description and is the
sextuple:
LO =< NumberFrame, Size, LI
hv
, LI
vv
, LI
vp
, LI
hp
>
where the first element denotes the number of the
frame where the object is located, the second element
corresponds with its size (number of valid linguistic
motion vectors associated with it) and the four last lin-
guistic intervals represents the velocity and position
of the object (as in the definition of linguistic motion
vector).
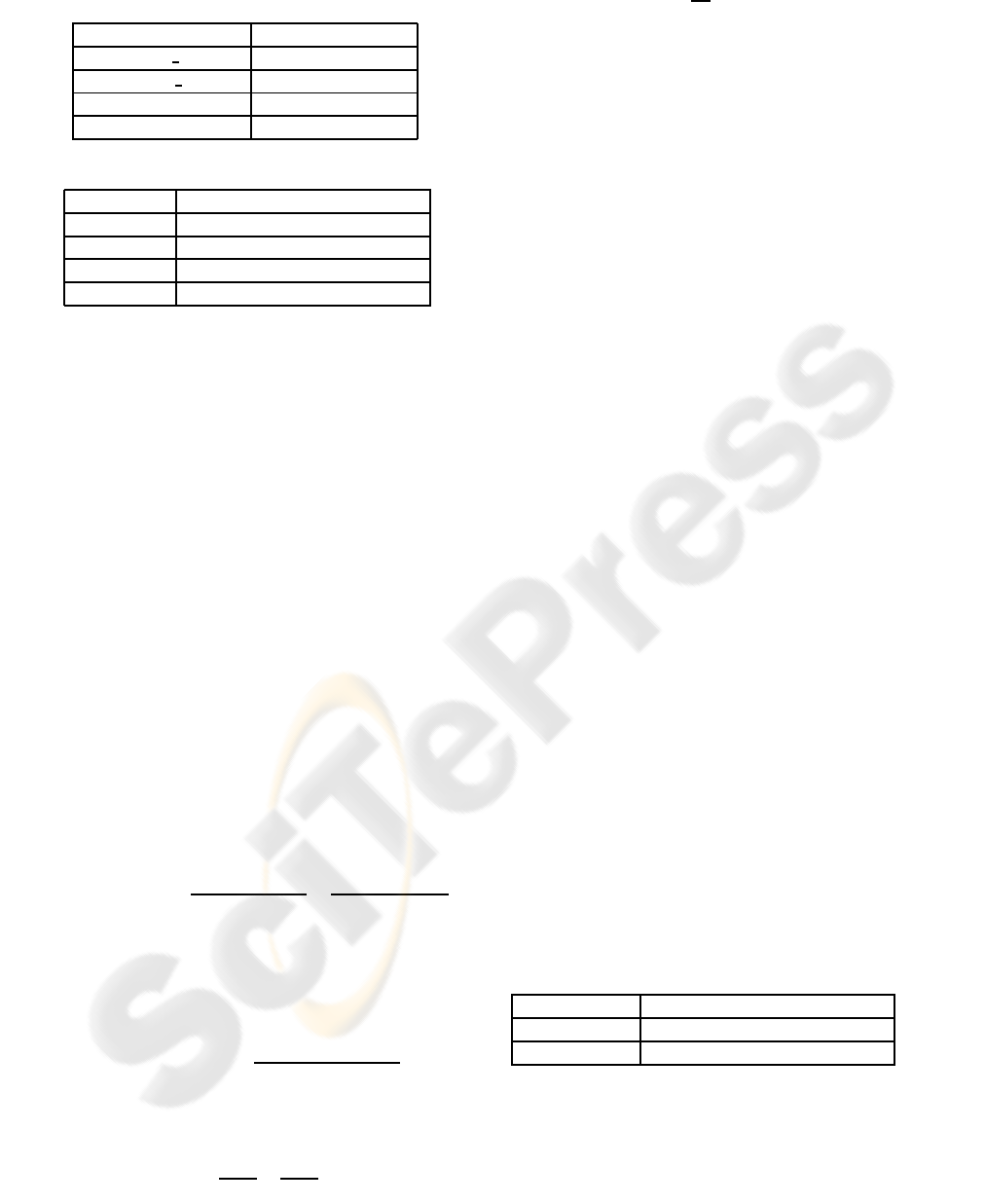
Table 4: Fuzzification of the motion vector data.
Data Linguistic Interval
right x LI
hv
down x LI
vv
macroblock row LI
vp
macroblock column LI
hp
Table 5: Linguistic motion vector in frame 39.
NumFrame 39
LI
hv
[Fast Left, 1]
LI
vv
[No Motion, 1]
LI
vp
[Very Up, 0,25], [Up, 0,75]
LI
hp
[Right, 0.5], [Very Right, 0.5]
4 INTRAFRAME
SEGMENTATION
The intraframe segmentation process is based in a dis-
tance measure, D, and a clustering of valid linguistic
motion vectors which are added to a linguistic object.
Each time a VLMV is incorporated, the conceptual
characterization of the LO is modified as is shown in
section 4.2.
4.1 Computation of the Distance
Measure
This distance measure is based on the Euclidean dis-
tances of the numbering order of the labels who com-
poses each fuzzy set. The Euclidean distance is se-
lected because the support length of each linguistic la-
bel in all the fuzzy sets is very similar. In another case,
we would proposethe selection of a distance measure-
ment based on the support length as in (Castro-Schez
et al., 2004). The used distance is defined as:
D(LI
c
j, p
− LI
d
j,q
) =
c+ (c+ p− 1)
2
−
d + (d + q− 1)
2
(4)
This distance is normalized (ND) between the in-
terval 0 and 1 dividing the result by the total number
of labels less 1 of each fuzzy set j.
ND(LI
c
j, p
− LI
d
j,q
) =
D(LI
c
j, p
− LI
d
j,q
)
NumLabels( j) − 1
(5)
For example, considering the fuzzy set in the fig-
ure 7 with a number of five labels:
D(LI
1
hp,1
, LI
2
hp,1
) =
1+(1)
2
−
1+(2)
2
= 2 − 1.5 = 0.5
ND(LI
1
hp,1
, LI
2
hp,1
) =
0.5
4
= 0.125
As the linguistic characterization of a VLMV and
a LO is composed of four linguistic intervals the to-
tal distance (TD) considered is the maximum of the
individual normalized distances:
TD(VLMV
x
, LO
y
) = max(ND
hv
, ND
vv
, ND
vp
, ND
hp
)
(6)
Once the total distance result is obtained, we con-
sider VLMV
x
and LO
y
are linguistically or conceptu-
ally similar if:
TD(VLMV
x
, LO
y
) < ε (7)
where ε would depend of the main objective of a con-
crete application or the size of the objects in the scene,
noise conditions,... For our general video sequences
and experiments, the best results are obtained with a
value for ε of 0.3
4.2 Weighted Aggregation of Vlmvs in a
Linguistic Object
Once calculated the distance described in section 4.1
between all the VLMVs (not previously been associ-
ated with a linguistic object) in the same frame with
respect to a linguistic object, the VLMV that mini-
mizes this distance and fulfills the condition shown in
the equation 7 must be aggregatedto the linguistic ob-
ject modifying its conceptual characterization as fol-
lows: if we consider VLMV
z
being the element to add
and LO
y
a linguistic object, the weighted aggregation
suggested increments the size parameter of LO
y
and
combines each one of the four linguistic intervals of
VLMV
z
with its corresponding in LO
y
. As described
in section 3.2 each LI is composed of a label and a
membership value. The new set of labels associated
to a LI is the result of the union of the labels of each
LI, nevertheless with the membership value we have
considered several options. For example, in table 6
each membership value has the same weight in the
final result.
Table 6: Weighted aggregation.
VLMV
z
(LI
vp
) [Very Up, 1]
LO
y
(LI
vp
) [Very Up, 0.25], [Up, 0.75]
Union [Very Up, 0.625], [Up, 0.375]
We consider this option has some problems. For
example, let us suppose the size of LO
y
is equal to
8 and VLMV
z
fulfills the distance conditions but it
is an isolated VLMV. Although the precision of the
system in the scope of approximate reasoning could
be considered a secondary objective, we propose that

when a VLMV
z
is aggregated to a LO
y
the character-
ization of this object, concretely its membership val-
ues must be pondered by the object size as showed in
the equations 8 to 10 (corresponding respectively to a
label in LO
y
and VLMV
z
, a label in LO
y
and a label in
VLMV
z
), in table 7 and in the corresponding examples
based in the values of table 6.
µ
′
LO
(SA
j
) =
µ
LO
(SA
j
) ∗ size(LO)
size(LO) + 1
+
µ
VLMV
(SA
j
)
size(LO) + 1
(8)
µ
vp
(VeryU p)=
1
9
+
0.25∗8
9
=0.11+0.22=0.33
µ
′
LO
(SA
j
) =
µ
LO
(SA
j
) ∗ size(LO)
size(LO) + 1
(9)
µ
vp
(UP)=
0.75∗8
9
=0.66
µ
′
LO
(SA
j
) =
µ
VLMV
(SA
j
)
size(LO) + 1
(10)
µ
vp
(UP)=
0.75
9
=0.083
Table 7: Weighted aggregation considering size of LO equal
than 8.
VLMV
z
(LI
vp
) [Very Up, 1]
LO
y
(LI
vp
) [Very Up, 0.25], [Up, 0.75]
Union [Very Up, 0.33], [Up, 0.66]
A problem detected in the experiments is an
overdescription of the object as occurs in the example
of table 8 where we consider the size of LO equal to
1. In this situation, we propose as result of the union,
when a LO has more than three label with member-
ship values greater than 0, the central label with mem-
bership value equal to 1.
Table 8: Weighted aggregation overdescription problem.
VLMV
z
(LI
vp
) [VU, 0.6], [Up, 0.4]
LO
y
(LI
vp
) [Up, 0.2], [CV, 0.8]
Union [VU, 0.3], [Up, 0.3], [CV, 0.4]
Proposed Union [Up, 1]
5 INTERFRAME
SEGMENTATION
In the interframe segmentation we have obtained the
conceptual description of the motion of every object
in a subset of the total individual frames. Now, the
correspondence between objects in each frame i.e. the
conceptual description of the trajectory of the objec-
tive in all the video sequence must be computed. We
have information about linguistic objects only in the
frames with motion information (P and B). If LO
x
(t)
is a linguistic object x in a frame t we search for
LO
y
(t +1) who minimizes the same measure distance
that was described in section 4.1. If no correspon-
dence is found or in frame t+1 there is no informa-
tion available, the search is extended to frames t+2,
t+3,...,t+n. In our experiments we consider the restric-
tions:
1. n is limited to 100 frames to avoid a possible con-
fusion with another object in motion which could
appear later in the scene
2. To establish a correspondence between two lin-
guistic objects their sizes must be about the same.
(a variation allowed of 2)
This set of restrictions can be interpreted as a first
approximation of a more complex database that must
be build to guarantee the system reliability in situa-
tions as occlusions, changing directions or velocities,
lack of motion, etc. So far, the interframe segmen-
tation process must be partially supervised by an ex-
pert that sometimes establishes real correspondences
between LO
x
(t) and LO
x
(t + r). Anyway, in this pa-
per we are trying to estimate the reliability of the in-
traframe segmentation process. In table 9 a partial
intraframe segmentation is shown. It can be observed
the linguistic descriptions are very similar (or equal)
and there is no information about the LO in a vast ma-
jority of frames.
Table 9: Interframe correspondences of linguistic objects.
Frame LI
hv
LI
vv
LI
vp
LI
hp
133 LL LU LD VR
138 LL, NL NM, LU LD VR
139 LL, NL NM, LU LD R, VR
140 LL, NL NM, LU LD R, VR
164 LL, NL NM, LU LD R, VR
6 EXPERIMENTAL RESULTS
We have done 9 experiments, three per video where
we defuzzificate the conceptual description that is
the output of the system obtaining a value for each
coordinate (x,y) representing the position of the ob-
ject in all the frames which store motion informa-
tion. Then we compare them with the real coordi-
nates (x,y) of the centre of the object obtained from
another application where the sequence of images is

showed and an expert click on the objective. The av-
erage quadratic error measure is used obtaining an ab-
solute error (pixels) and a percentage error (absolute
error/frame width or height in pixels). Figures from 8
to 10 are our video samples and in table 10 is shown
our system’s output (identical descriptions in contigu-
ous frames are shown in the same row of the table) for
the video sample 3 using as input only the motion vec-
tors backward predicted. The percentage error calcu-
lated for all the experiments once the output has been
defuzzificated is presented in table 11 and graphically
in the concrete experiment (video3, backward) for the
coordinate x and y in figures 11 and 12 respectively.
Figure 8: Object trajectory in video 1.
Figure 9: Object trajectory in video 2.
7 CONCLUSION
In this work we have proposed a method for con-
structing a high level conceptual description of the
motion of objects directly from compressed domain
with minimal decoding, concretely, using only infor-
mation stored in motion vectors. Although the tech-
nique does not incorporate any a priory information
about the test videos, the percentage error is around 6
per cent. Besides, we obtain this measure error com-
paring a semantic description with numerical coordi-
Figure 10: Object trajectory in video 3.
Table 10: System’s output video 3 with backward predic-
tion.
Initial LI
hv
LI
vv
LI
vp
LI
hp
134 LL NM, LU D VR
146 LL NM, LU D R, VR
153 LL NM D R, VR
159 LL NM, LU D R
164 LL NM, LU CV, D CH, R
165 LL NM CV, D CH, R
177 LL NM CV CH
189 LL NM CV L, CH
177 LL NM CV CH
192 LL NM CV L, CH
192 LL NM CV L
201 NM, LL NM CV L
210 NM, LL NM LU, CV L
210 NM, LL NM LU, CV VL, L
nates (x,y) of the object because no method of com-
parison between our system’s output and a human-
generated description, with its inherent vagueness and
imprecision, can be made.
The novelties of this study are (i) a statistical
study of the amount and validity of the motion vectors
where we can determine that the use of backward pre-
dicted motion vectors from the point of view of output
precision and efficiency is the best option (ii) the seg-
mentation process is always made by using high level
conceptual descriptions with semantic meaning.
The main advantages of the system are (i) Effi-
ciency as we work in the compressed domain and the
information in this domain is only partially decoded.
(ii) The operation of the system is very simple and is
based in a measure distance and a clustering process
based on this distance. (iii) The semantic output al-
low to interpret easily the characteristics of the mo-
tion of an object. (iv) The reliability of the system is
good more still if we know that the design of linguis-
tic labels is general and the interframe process is very
basic.
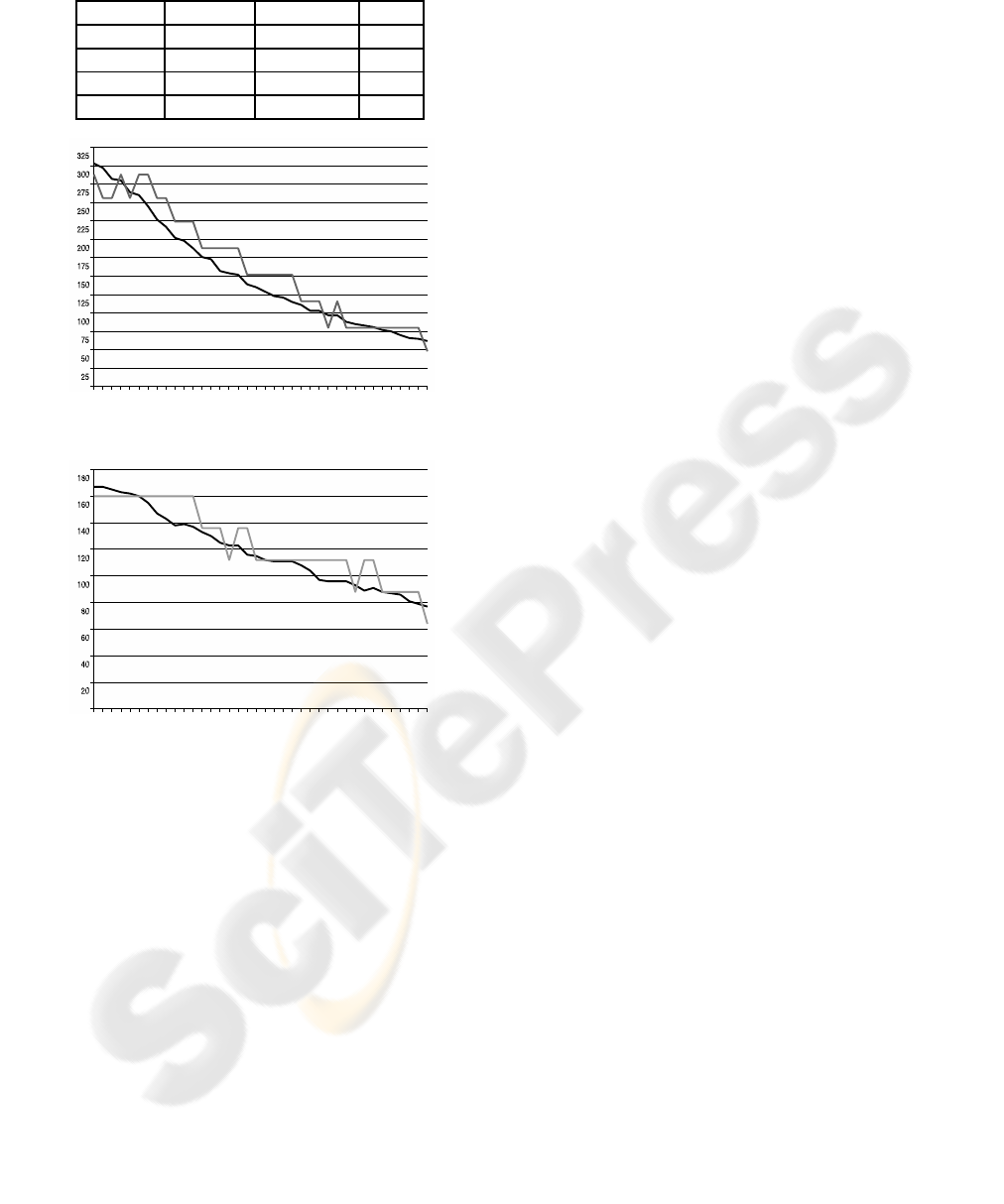
Table 11: Total error.
Video Forward Backward Both
1 5.3% 5.4% 5.1%
2 7.2% 7% 7.2%
3 5.3% 6% 6.2%
Average 5.9% 6.1% 6.2%
Figure 11: Comparison for coordinate x in video 3.
Figure 12: Comparison for coordinate y in video 3.
In future works, (i) we must design the linguis-
tic labels making restrictions about the characteristics
of the video signal and of the objective (size, list of
possible motions, ...) (ii) make fully automated the
segmentation interframe process incorporating some
kind of knowledge like a database of rules to avoid in-
congruences between directions of velocities and po-
sitions corresponding with peaks in the function.
ACKNOWLEDGEMENTS
This work has been funded by the Regional Gov-
ernment of Castilla-la Mancha (PAC06-0141 and
PBC06-0064).
REFERENCES
Antani, S., Kasturi, R., and Jain, R. (2001). A survey on
the use of pattern recognition methods for abstraction,
indexing and retrieval of images and video. In Pattern
Recognition. Elservier Science.
Ardizzone, E., Cascia, M. L., Avanzato, A., and Bruna, A.
(1999). Video indexing using mpeg motion compen-
sation vectors. In International Conference on Multi-
media Computing and Systems. IEEE.
Castro-Schez, J., Castro, J., and Zurita, J. (2004). Method
for acquiring knowledge about input variables to ma-
chine learning algorithm. In IEEE Transactions on
Fuzzy Systems. IEEE.
Dubois, D. and H.Prade (1980). Fuzzy sets and systems.
Theory and applications. Academic press, New York,
1st edition.
Gilvarry, J. (1999). Calculation of motion using motion vec-
tors extracted from an mpeg stream. In Technical Re-
port. Dublin City University.
Kim, N., Kim, T., and Choi, J. (2002). Motion analysis
using the normalization of motion vectors on mpeg
compressed domain. In International Technical Con-
ference on Circuits/Systems, Computers and Commu-
nications. IEICE.
Moreno-Garcia, J., Rodriguez-Benitez, L., Castro-Schez, J.,
and Jimenez, L. (2004). A direct linguistic induction
method for systems. In Fuzzy Sets and Systems. Inter-
national Fuzzy Systems Association.
Pilu, M. (2001). On using raw mpeg motion vectors to de-
termine global camera motion. In Pattern Recogniton
Letters. Elsevier Science.
Rapantzidos, K. and Zervakis, M. (2005). Robust optical
flow estimation in mpeg sequences. In International
Conference on Acoustics, Speech, and Signal Process-
ing. IEEE.
Rodriguez-Benitez, L., Moreno-Garcia, J., Castro-Schez,
J., and Jimenez, L. (2005). Linguistic motion de-
scription for an object on mpeg compressed domain.
In Eleventh International Fuzzy Systems Association
World Congress. International Fuzzy Systems Associ-
ation.
Venkatesh, R., Anantharaman, B., Ramakrishnan, K., and
Srinivasan, S. (2001). Compressed domain action
classification using hmm. In Pattern Recogniton Let-
ters. Elsevier Science.
Venkatesh, R. and Ramakrishnan, K. (2002). Background
sprite generation using mpeg motion vectors. In In-
dian Conference on Computer Vision. Uni-Trier.
Yoon, K., DeMenthon, D., and Doerman, D. (2000). Event
detection from mpeg video in the compressed domain.
In 15th Conference on Pattern Recognition. IEEE.
Zadeh, L. (1960). Fuzzy set. In Information and Control.
Zadeh, L. (1975). The concept of a linguistic variable and
its applications to approximate reasoning. In Informa-
tion Science.
