AN ACTIVE STEREOSCOPIC SYSTEM FOR ITERATIVE 3D

SURFACE RECONSTRUCTION

Wanjing Li

Laboratory LE2i,University of Burgundy, Dijon, France

Laboratry i3Mainz, University of Applied Sciences, Mainz, Germany

Franck. S. Marzani, Yvon Voisin

Laboratory LE2i,University of Burgundy, Dijon, France

Frank Boochs

Laboratory i3Mainz, University of Applied Sciences, Mainz, Germany

Keywords: Active vision, 3D surface reconstruction, calibration, 3D triangular mesh, projector-camera system, adaptive

pattern projection, iterative reconstruction, surface curvature.

Abstract: For most traditional active 3D surface reconstruction methods, a common feature is that the object surface is

scanned uniformly, so that the final 3D model contains a very large number of points, which requires huge

storage space, and makes the transmission and visualization time-consuming. A post-process then is

necessary to reduce the data by decimation. In this paper, we present a newly active stereoscopic system

based on iterative spot pattern projection. The 3D surface reconstruction process begins with a regular spot

pattern, and then the pattern is modified progressively according to the object’s surface geometry. The

adaptation is controlled by the estimation of the local surface curvature of the actual reconstructed 3D

surface. The reconstructed 3D model is optimized: it retains all the morphological information about the

object with a minimal number of points. Therefore, it requires little storage space, and no further mesh

simplification is needed.

1 INTRODUCTION

In the field of 3D surface reconstruction and

metrology, including industrial applications,

stereoscopic systems are becoming increasingly

important. They can be divided into two categories:

passive or active (Battle et al., 1998; Horaud et al.,

1995).

In passive stereoscopic systems, cameras are

observing the object as it is without generating

optical information. Such systems use multiple

camera views to acquire the 3D object surface

information. In case of single camera systems, the

camera has to be moved to at least two known

positions around the object and takes images

sequentially at each position; in other cases, two or

more cameras being fixed in different positions take

images at the same time (Battle et al., 1998).

In active stereoscopic systems, a light projection

device is added to produce individual signals,

generate texture or code uniquely each surface

element (Battle et al., 1998). Individual signals

might be produced by a moving laser beam being

observed in a sequence of images; a certain texture

can be generated by projecting full-field light pattern

onto the object surface, so that each camera only

needs to take one image; for coded light approaches,

a projection sequence is necessary if the coding is

temporal, it is more sensitive to object appearance

and external light conditions (Krattenthaler et al.,

1994).

If we define respectively coordinate references

for the object (called “world reference”) and each

camera (called “camera reference”), the geometrical

relationship between the world reference and the

camera references can be described by extrinsic

parameters of the cameras, whereas the

Li W., S. Marzani F., Voisin Y. and Boochs F. (2007).

AN ACTIVE STEREOSCOPIC SYSTEM FOR ITERATIVE 3D SURFACE RECONSTRUCTION.

In Proceedings of the Second International Conference on Computer Vision Theory and Applications, pages 78-84

DOI: 10.5220/0002065500780084

 SciTePress

mathematical behavior of a camera is given by

intrinsic parameters. The intrinsic and extrinsic

parameters (that will be called “calibration

parameters” for simplification in the rest of the

paper) can be obtained respectively by camera

calibration and orientation process. Different

approaches were proposed (Faugeras et al., 1986;

Grün et al., 1992; Legarda-Saenz et al., 2004;

Marzani et al., 2002), and Garcia et al. (2000) made

a comparison of some approaches.

To determine the surface geometry of an object,

the 2D coordinates of a surface element in the

images are extracted respectively. If the calibration

parameters are known, the 3D coordinates of this

point in world reference can be calculated by

triangulation using all image rays to the object point.

In case of passive stereoscopic systems, image

rays are identified by using available texture on the

surface. For objects with low texture information,

the identification of the image rays becomes very

difficult; whereas in active systems, the projector

creates a synthetic texture on the surface of the

object, which simplifies the identification of image

rays, thus the rate of detected object points can be

highly increased.

For most of the previous pattern projection

methods, their common characteristic is the use of

pattern with a uniform resolution for the whole

object without considering the geometrical structure

of the surface. Such methods are necessary if the

object has complex surface geometry. However, for

those with relatively simple surface geometry, the

reconstructed 3D model can contain large number of

useless data which describes a plane area, and it can

easily reach to a size of gigabytes. The sheer amount

of data not only exhausts the main memory

resources of common desktop PCs, but also exceeds

the 4 gigabyte address space of 32-bit machines

(Isenburg et al., 2003); it makes the subsequent

processing difficult (ex., save, transmission,

rendering, etc.). Therefore, the further mesh

simplification is often necessary. However, it is

difficult to obtain an optimized model which retains

all morphological information about the object with

a minimum of points.

In this paper, we present a newly active

stereoscopic system based on an iterative projection

concept. The reconstruction process begins with a

regular spot pattern. After each iteration, the local

surface curvature of the actual reconstructed 3D

surface is estimated, and the density and distribution

of pattern spots are then modified for the next

iteration, thus the reconstructed 3D surface is refined

progressively. The final reconstructed 3D model was

proved to be optimized and needs much less storage

space compared to that obtained by traditional

solutions. This concept has been validated in

simulation working mode (Li et al., 2006). In this

paper, we focus on reality working mode.

The article is organized as follows: first, we

briefly present the 3D surface reconstruction system;

then we describe the following steps: system

calibration, initial pattern projection and iterative

process; finally, some reconstruction results are

given before we conclude and show perspectives.

2 SYSTEM DESCRIPTION

As shown in figure 1, the system consists of two

CCD cameras (Oscar F-510C, resolution:

2588x1958) and one LCD projector (Panasonic PT-

LB10E, resolution: 1024x768). A computer is

connected to them as the central control unit. It is

based on an iterative scheme (see figure 2), and is

controlled by a program developed in Matlab

language. A graphical interface is provided to user.

Figure 1: System setup.

Before the 3D reconstruction process begins, the

two cameras and the video projector should be

calibrated to obtain the calibration parameters. The

projector then projects initially a regular spot matrix

pattern onto the object. Each camera acquires an

image of the illuminated object. We extract the 2D

spot coordinates in the two images and then match

them. With the known calibration parameters, we

calculate the corresponding 3D object point

coordinates. A 3D surface mesh will then be

generated from the reconstructed 3D point cloud.

For each vertex of the 3D mesh, we estimate its

Gaussian curvature to decide if new spots should be

projected around it at next iteration. Finally, we

verify if the “condition of stop” is satisfied. If it is

the case, the process stops and the final

reconstructed 3D surface is obtained; otherwise, a

AN ACTIVE STEREOSCOPIC SYSTEM FOR ITERATIVE 3D SURFACE RECONSTRUCTION

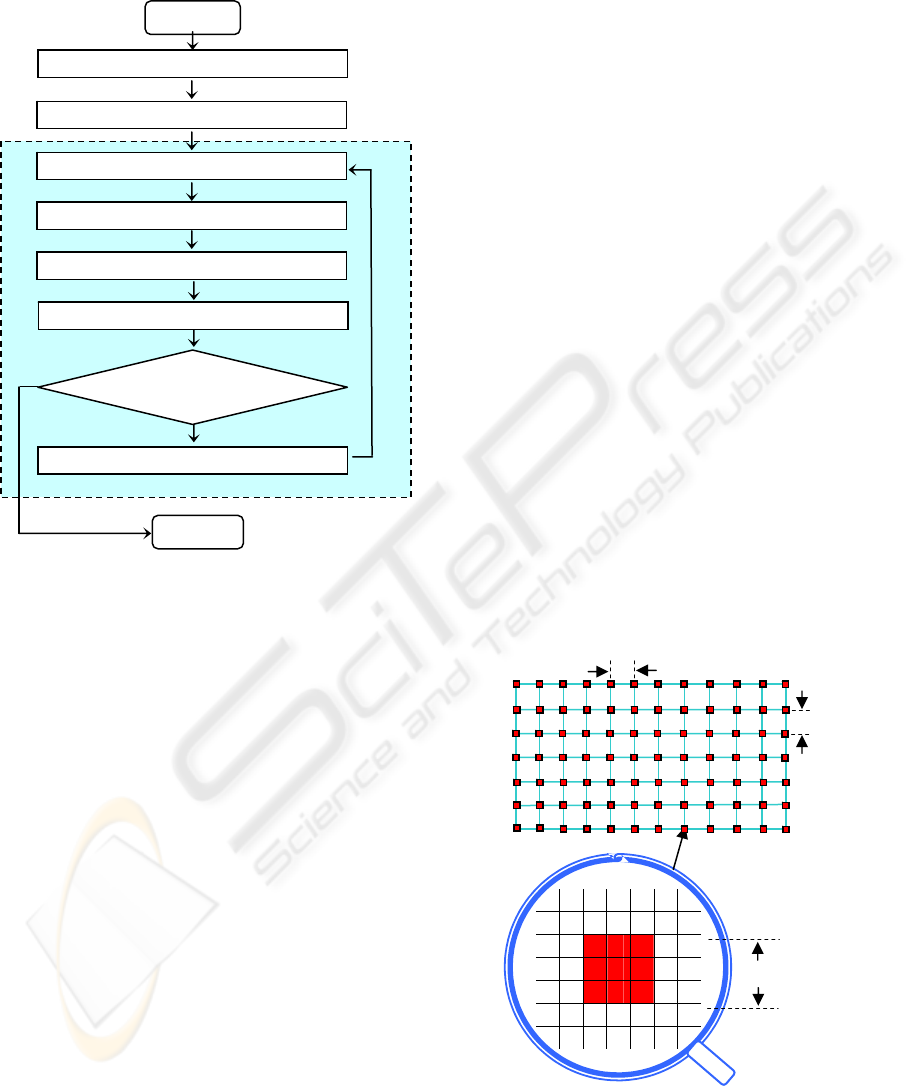
new pattern is generated, and the process goes back

to the image acquisition step and continues.

Figure 2: Iterative scheme.

In the following paragraphs, we describe how

the process works at each step. To simplify the

description, we suppose that P (u

v) is a pattern spot

and that V (x

y, z) is its representation on the object.

V can also be a vertex of current 3D triangular mesh

which approximates the object surface.

3 SYSTEM CALIBRATION

The calibration of the two cameras and the video

projector is indispensable. Actually, in our system,

the calculation of 3D point coordinates is based on

the images acquired by the two cameras. Therefore

we need to know the calibration parameters of the

two cameras; those of the projector have also to be

known for new pattern generation (see 5.6).

CCD camera and LCD projector can both be

described by a geometrical model called “pinhole”

(Lathuilière et al., 2003). In such a model, the

extrinsic parameters are the rotation matrix R and

the translation matrix T; these two matrices describe

the geometrical relationship between the world

reference and the camera/projector reference (Tsai,

1986). The intrinsic parameters are:

 f : the focal length;

 O (u

, v

) : the intersection point between the

image plan and the optical axis of the camera;

 k

: the vertical scale factor (pixels/mm) in

image plan;

 k

: the horizontal scale factor.

To get all these parameters, the system is

calibrated in two steps by applying Faugeras-

Toscani approach (Faugeras et al., 1986). At the first

step, a calibration target is used to obtain the

calibration parameters of the two cameras without

using the video projector. At the second step, the

projector projects a certain spot pattern onto the

object. Each camera then acquires an image of the

object. By using the calibration parameters of the

two cameras obtained at the first step, we can

calculate the 3D coordinates of the object points

from the image points, so that the calibration

parameters of the video projector can be obtained

from the projected 2D pattern points and the

reconstructed 3D object points.

4 INITIAL PATTERN

The initial pattern is defined by 4 values (in pixels):

 (u

, v

): upper left point coordinates;

 (u

, v

): down right point coordinates;

 s: spot size;

 d

: distance between two adjacent spots.

Figure 3: Definition of the initial pattern.

s = 3 pixels

, v

)

, v

)

3D surface mesh generation

Yes

System calibration

ew pattern generation and projection

“Condition of stop”

satisfied?

END

BEGIN

Initial pattern

rojection

Image acquisition

3D point cloud reconstruction

Local surface curvature estimation

Iterative process

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

Figure 3 illustrates how the initial pattern is

defined by these values. The definition of initial

pattern is quite important. If the object has some

small surface variations, the spots should be dense

enough to cover all these small areas. Otherwise, the

reconstructed initial 3D surface might be flat in

these areas. In consequence, at the next iteration, no

pattern spot would be projected around these areas

since its local surface curvature is not strong enough.

As a result, the final reconstructed 3D model might

lose partially geometrical information.

5 ITERATIVE PROCESS

5.1 Image Acquisition

Once the pattern is projected, each camera takes an

image of the illuminated object. These two images

are saved in the memory for 3D point cloud

reconstruction.

5.2 3D Point Cloud Reconstruction

The process of 3D point cloud reconstruction can be

divided into 3 steps:

 2D image point detection;

 2D image point matching;

 3D object point coordinates calculation.

To detect image points, we first apply several

image processing techniques, such as filtering,

thresholding, and contour recognition, to get the

boundary of the spot. Then, all pixels within the

boundary are considered for a weighted calculation

of the center of gravity, which gives the center of the

image ray.

The correspondence problem then should be

resolved, i.e., to identify, for a given point in one

image, its correspondence in the other one (see

figure 4). Since the images are calibrated and

oriented in space, we can simplify the

correspondence problem by applying some

geometrical constraints. The most important one is

based on the fact that corresponding points are

imaged on epipolar lines. Some other constraints

come from the relative position of two adjacent

object points, or the probability of having major

changes in the distance from the image to object

(Böhler et al., 2006).

Finally, for each pair of matched image points,

by using the calibration parameters for each camera,

we calculate, by ray intersection, the 3D coordinates

of the corresponding object point.

(a) (b)

Figure 4: An example of acquired images, (a) Image

acquired by left camera, (b) Image acquired by right

camera.

5.3 Mesh Generation

Once the 3D point cloud is obtained, we generate a

3D surface mesh by Delaunay triangulation. The

Delaunay triangulation is generally unique. It has the

property that the outcircle of every triangle does not

contain any other point. The Delaunay triangulation

is the dual structure of the Voronoi diagram

(Kanaganathan et al., 1991).

5.4 Surface Curvature Estimation

From a theoretical point of view, triangular meshes

do not have any curvature at all, since all faces are

flat and the curvature is not properly defined along

edges and at vertices because the surface is not C

differentiable. However, thinking of a triangular

mesh as a piecewise linear approximation of an

unknown smooth surface, the curvature of that

unknown surface might be calculated using the

information given by the triangular mesh itself (Dyn

et al., 2001). A normal curvature is the

generalization of surface curvatures. Given a point P

on the surface S and a direction

lying in the

tangent plane of the surface S at P, the normal

curvature is calculated by intersecting S with the

plane spanned by P, the normal to S at P, and

. The

normal curvature is the signed curvature of this

curve at P. If we compute the normal curvature for

all values of

in the tangent plane at P, we will get

a maximum value k

and a minimum value k

in two

orthogonal directions. k

and k

are called principal

curvatures.

The Gaussian curvature K (also called total

curvature) and mean curvature H are differential

invariant properties which depend only upon the

surface’s intrinsic geometry, and play a very

Same object point

AN ACTIVE STEREOSCOPIC SYSTEM FOR ITERATIVE 3D SURFACE RECONSTRUCTION

important role in the theory of surfaces. They are

defined as follow:

K = k

× k

, (1)

H = (k

+ k

) / 2. (2)

In our work, we chose the Gaussian curvature to

evaluate the local surface curvature, since for a

minimal surface, the mean curvature is zero

everywhere, whereas Gaussian curvature may vary

in different zones; besides, the sign of Gaussian

curvature gives extra information about the type of

the local piecewise surface. A positive Gaussian

curvature value means the surface is locally either a

peak or a valley. A negative value means the surface

locally has a saddle. And a zero value means the

surface is flat in at least one direction (i.e., both a

plane and a cylinder have zero Gaussian curvature)

(Alboul et al., 2005).

As we can see, the Gaussian curvature and mean

curvature are defined only for twice differentiable

) surfaces. To get 3D surface curvature

information, different approaches have been

proposed to estimate Gaussian and mean curvature

(Alboul et al., 2005; Surazhsky et al., 2003; Peng et

al., 2003). Surazhsky et al. (2003) compared five

curvature estimation algorithms, and drew a

conclusion that the Gauss-Bonnet scheme is the best

algorithm for the estimation of Gaussian curvature.

We therefore estimate the curvature as follows:

Vertex V

is considered as a neighbor of vertex V

if the edge

belongs to the mesh. Denote the set

of neighbors of V by {V

| i =1, 2, ..., n}, the set of

triangles containing V by {T

= Δ (V

, V, V

(i+1)

mod n

) |

i =1, 2, ..., n}, and the set of angles between V and

its two successive neighbors by {

= (V

, V, V

(i+1)

mod n

) | i =1, 2, ..., n} (see figure 5-(a)). According to

the Gauss-Bonnet scheme (Surazhsky et al., 2003),

the Gaussian curvature K at vertex V is estimated as

(3)

where A is the

sum of the areas of triangles T

around the vertex V.

This estimation method works well when vertex

V is close enough to its neighbors. Obviously, it is

not our case, since we start from a rough 3D surface

mesh and refine it progressively. In (Alboul et al.,

2005), Alboul et al. indicated that we can ignore A

and simply estimate the Gaussian curvature K at

vertex V as in (4):

5.5 “Condition of Stop” Verification

At the end of each iteration, the condition of stop is

verified by the following algorithm:

Target = {};

For each vertex V of current mesh

K = Gaussian curvature of V

If K < t

Delete V from the mesh;

Else if K > t

d = average distance between V

and all its neighbors;

If d > t

Target = Target + {V};

End

If Target == {}

Process stops;

Else

Generate new pattern;

End

where t

is the pre-defined threshold for “weak

curvature”; t

is the threshold for “strong curvature”;

and t

is the threshold for “minimal average distance

to neighbors”. Actually, in some cases, even after a

great number of iterations, the local surface

curvature K of V is always much higher than t

Therefore, to avoid infinite iteration, we introduced

the threshold t

5.6 New Pattern Generation

To generate the new pattern, firstly, for each target

vertex V obtained at previous step, if it has “closed”

neighborhood (see figure 5), we calculate the 2D

coordinates of its corresponding pattern spot P by

using the calibration parameters of the video

projector. Then eight new spots are added around it

in the new pattern. A single value d is enough to

specify their positions (see figure 6).

(a) (b)

Figure 5: Different types of vertex neighborhood in 3D

triangular mesh: (a) “closed” neighborhood, (b) not

“closed” neighborhood.

(

)

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

Figure 6: New pattern generation from a target pattern

spot.

Since the density of the 3D triangular mesh

increases after each iteration, the value of d has to be

adapted to the current 3D mesh. We therefore set the

value of d according to the average distance D

between the vertex V and all its neighbors in the

current 3D mesh as: d = r×D, where r is a ratio pre-

configured by user, it can be ½, ¼, or

, etc.

“Old” pattern spots will not be added into new

patterns because their reconstruction has already be

done. However, we keep the 3D point cloud

obtained at each iteration, so that they can be used

for 3D mesh generation at next iteration, thus the 3D

model is refined progressively.

Finally, we optimize the generated new pattern by

deleting those spots which are too close to each

other, so that at the next iteration, the 2D image

point detection and the 2D point matching will be

simplified.

6 RESULTS

We tested our system on several real objects. In this

paper, we show the reconstruction results of a mask,

since it has partial complex surface curvature. The

size of the mask is 150 mm (l) × 200 mm (h) ×130

mm (w). Figure 7 shows an example of

reconstruction results for the mask. In this example,

= 0.001, t

= 0.04, t

= 5 mm, r =

. The initial

pattern was defined as follows:

 (u

, v

) = (100,100);

 (u

, v

) = (700,760);

 s = 3 pixels;

 d

= 25 pixels.

To evaluate the quality of the reconstructed 3D

surface by our system, we scanned the mask by

using a traditional method, i.e. by projecting a

vertical stripe and shifting it from left to right, pixel

by pixel, the 3D surface obtained contains 10177

points. We then compared it to the one obtained by

our system by calculating the distance error, it

showed that the error in distance is very slight: The

average error is only 0.19 mm; and the maximal

error is 0.32mm (see figure 8). Besides, we can see

that the 3D surface obtained by traditional method

contains 10177 points, whereas the one obtained by

our system contains only 770 points, which means

that the number of points of the 3D surface was

reduced more than 90%.

(a) (b)

Figure 7: Reconstructed 3D surface of the mask, (a) initial

3D surface - 152 points, (b) Final 3D surface - 770 points.

(a) (b)

Figure 8: (a) 3D surface obtained by traditional method -

10177 points, (b) distance error between the 3D surface

reconstructed by using our approach and the one issued

from traditional method.

7 CONCLUSIONS

We presented an adapted 3D surface reconstruction

approach based on active vision system. The concept

is to restrict data capture to characteristic surface

parts during the image acquisition process, thus the

reconstructed 3D model will be ensured to be fitted

to the morphology of an object. The system projects

iteratively spot patterns adapted to the object surface

geometry. At each iteration, we calculate the local

AN ACTIVE STEREOSCOPIC SYSTEM FOR ITERATIVE 3D SURFACE RECONSTRUCTION

surface curvature for each vertex of the actual 3D

mesh and decide where to project more points.

This approach was proved to be very efficient,

because the reconstructed 3D surface needs much

less storage space compared to that obtained by

traditional method and does not need a post-process

for decimation. The quality of reconstructed 3D

surface is very satisfactory: compared to the one

issued from traditional method, the 3D surface of the

mask obtained by applying our approach has an

average distance error of less than 0.2 mm. The

whole reconstruction process takes only several

minutes. Compared to the traditional method, our

system is not faster. However, the later time-

consuming mesh simplification procedure can be

avoided since the 3D model obtained is optimized.

Our future work will focus on the improvement

of the system. Special efforts will be made on image

processing, surface curvature estimation and the

generation of new patterns. Once the system

becomes robust, we hope to apply this 3D

reconstruction approach to industrial application,

such as quality control, etc.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the support of

European Social Funds (France), University of

Applied Sciences in Mainz (Germany), and Regional

Council of Burgundy (France).

REFERENCES

Alboul, L., Echeverria G., Rodrigues, M., 2005. Discrete

curvatures and gauss maps for polyhedral surfaces, in

European Workshop on Computational Geometry

(EWCG), Eindhoven, the Netherlands, pp. 69–72.

Battle, J., Mouaddib, E., Salvi, J., 1998. Recent progress

in coded structured light as a technique to solve the

correspondence Problem: a Survey, Pattern

Recognition, 31(7), pp. 963-982.

Böhler, M., Boochs, F., 2006. Getting 3D shapes by means

of projection and photogrammetry, Inspect, GIT-

Verlag, Darmstadt.

Dyn, N., Hormann, K., Kim S. J., Levin, D., 2001.

Optimizing 3D triangulations using discrete curvature

analysis, Mathematical Methods for Curves and

Surfaces, Oslo 2000, Nashville, TN, pp.135-146.

Faugeras, O. D., Toscani, G., 1986. The calibration

problem for stereo, in Proc. Computer Vision and

Pattern Recognition, Miami Beach, Florida, USA,

pp.15-20.

Garcia, D., Orteu, J.J., Devy, M., 2000. Accurate

Calibration of a Stereovision Sensor: Comparison of

Different Approaches, 5th Workshop on Vision

Modeling and Visualization (VMV'2000), Saarbrücken,

Germany, pp.25-32.

Grün, A., Beyer, H., 1992. System calibration through

self-calibration, Workshop on Calibration and

Orientation of Cameras in Computer Vision,

Washington D.C..

Horaud, R., Monga, O., 1995. Vision par ordinateur:

outils fondamentaux, Hermès, 2

edition.

Isenburg, M., Lindstrom, P., Gumhold, S., Snoeyink, J.,

2003. Large mesh simplification using processing

sequences, in Proc. Visualization'03, pp. 465-472.

Kanaganathan, S., Goldstein, N.B., 1991. Comparison of

four point adding algorithms for Delaunay type three

dimensional mesh generators, IEEE Transactions on

magnetics, 27(3).

Krattenthaler, W., Mayer, K.J., Duwe, H.P., 1994. 3D-

surface measurement with coded light approach, In

Proc. of the 17th meeting of the Austrian Association

for Pattern Recognition on Image Analysis and

Synthesis, pp. 103-114.

Lathuilière, A., Marzani, F., Voisin, Y., 2003. Calibration

of a LCD projector with pinhole model in active

stereovision applications. Conference SPIE :Two- and

Three-Dimensional Vision Systems for Inspection,

Control, and Metrology, Rhode Island, USA, 5265,

pp. 199-204.

Legarda-Saenz, R., Bothe, T., Jüptner, W.P., 2004.

Accurate Procedure for the Calibration of a Structured

Light System, Optical Engineering, 43(2), pp.464-

471.

Li, W., Boochs, F., Marzani, F., Voisin, Y., 2006.

Iterative 3D surface reconstruction with adaptive

Pattern projection, in Proc. of the Sixth IASTED

International Conference on Visulatization, Imaging

and Image Processing (VIIP), Palma De

Mallorca, Spain, pp.336-341.

Marzani, F., Voisin, Y., Diou, A., Lew Yan Voon, L.F.C.,

2002. Calibration of a 3D reconstruction system using

a structured light source, Journal of Optical

Engineering, 41 (2), pp. 484-492.

Peng, J., Li, Q., Jay kuo C.C., Zhou, M., 2003. Estimating

Gaussian Curvatures from 3D meshes. SPIE

Electronic Image, vol.5007, pp. 270-280.

Surazhsky, T., Magid, E., Soldea, O., Elber, G., Rivlin, E.,

2003. A comparison of gaussian and mean curvatures

estimation methods on triangular meshes, in IEEE

International Conference on Robotics & Automation.

Tsai, R.Y., 1986. An efficient and accurate camera

calibration technique for 3D machine vision, IEEE

Computer Vision and Pattern Recognition, Miami

Beach Florida, pp.364-374.

VISAPP 2007 - International Conference on Computer Vision Theory and Applications