VARIATIONAL POSTERIOR DISTRIBUTION APPROXIMATION IN

BAYESIAN EMISSION TOMOGRAPHY RECONSTRUCTION USING

A GAMMA MIXTURE PRIOR

Rafael Molina

, Antonio L´opez

, Jos´e Manuel Mart´ın

and Aggelos K. Katsaggelos

Departamento de Ciencias de la Computaci´on e I.A., Universidad de Granada, 18071 Granada, Spain

Departamento de Lenguajes y Sistemas Inform´aticos, Universidad de Granada, 18071 Granada, Spain

Department of Electrical Engineering and Computer Science, Northwestern University, Evanston, Illinois 60208-3118

Keywords:

Image reconstruction, parameter estimation, Bayesian framework, variational methods, Tomography images.

Abstract:

Following the Bayesian framework we propose a method to reconstruct emission tomography images which

uses gamma mixture prior and variational methods to approximate the posterior distribution of the unknown

parameters and image instead of estimating them by using the Evidence Analysis or alternating between the

estimation of parameters and image (Iterated Conditional Mode (ICM)) approach. By analyzing the posterior

distribution approximation we can examine the quality of the proposed estimates. The method is tested on real

Single Positron Emission Tomography (SPECT) images.

1 INTRODUCTION

SPECT (Single Photon Emission Computed Tomog-

raphy) and PET (Positron Emission Tomography) are

non invasive techniques which are used in Nuclear

Medicine to take views of a isotope distribution in

an patient. Since SPECT and PET obtain images

via emission mode, both techniques are referred to as

emission tomography.

In this paper, we address the problem of the re-

construction of emission tomography images. We

propose the use of the hierarchical Bayesian frame-

work to incorporate knowledge on the expected char-

acteristics of the original image in the form of a mix-

ture of gamma distributions, to model the observa-

tion process, and also to include information on the

unknown parameters in the model in the form of hy-

perprior distributions. Then, by applying variational

methods to approximate probability distributions we

estimate the unknown parameters and the underlying

original image.

The paper is organized as follows. In section 2

the Bayesian modeling and inference for our problem

is presented. The used probability distributions for

emission tomography images are formulated in sec-

tion 3. The Bayesian analysis and posterior proba-

bility approximation to obtain the parameters and the

original image is performed in section 4. The applica-

tion of this method to a real SPECT study is described

in section 5 and, ﬁnally, section 6 concludes the paper.

2 BAYESIAN FORMULATION

Let the object to be estimated be represented by a

vector x of N lexicographically ordered voxels x =

,... ,x

}. The observed, noisy data from which x

is to be estimated is given by the vector y, comprising

lexicographically ordered elements y = {y

,... ,y

where M is the number of detectors in the tomography

system.

The Bayesian formulation of the Nuclear Medi-

cine image reconstruction problem requires the def-

inition of the joint distribution p(Ω,x,y) of the ob-

servation y, the unknown original image x, and the

hyperparameters Ω, describing their distributions.

To model the joint distribution we utilize the

hierarchical Bayesian paradigm (see, for example

(Molina et al., 1999; Galatsanos et al., 2002)). In

the hierarchical approach we have two stages. In the

ﬁrst stage, knowledge about the structural form of the

165

Molina R., López A., Manuel Martín J. and K. Katsaggelos A. (2007).

VARIATIONAL POSTERIOR DISTRIBUTION APPROXIMATION IN BAYESIAN EMISSION TOMOGRAPHY RECONSTRUCTION USING A GAMMA

MIXTURE PRIOR.

In Proceedings of the Second Inter national Conference on Computer Vision Theory and Applications, pages 165-173

DOI: 10.5220/0002066001650173

 SciTePress

observation noise and the structural behavior of the

underlying image is used in forming p(y | x,Ω) and

p(x | Ω), respectively. In the second stage a hyper-

prior on the hyperparameters is deﬁned, thus allowing

the incorporation of information about these hyperpa-

rameters into the process.

Then the following joint distribution is deﬁned for

Ω, x, and y,

p(Ω,x,y) = p(Ω)p(x | Ω)p(y | x,Ω), (1)

and inference is based on p(Ω,x | y) (see

(Mohammad-Djafari, 1995), (Mohammad-Djafari,

1996)).

We can alternate the maximization of p(Ω,x | y)

with respect to Ω and x (the ICM approach), (Hsiao

et al., 2002). However, this alternative maximization

does not take into account the uncertainty in the orig-

inal image when estimating the unknown parameters

of the model and the consequential effect on the esti-

mation of these parameters. An alternative methodol-

ogy consists of estimating the hyperparameters in Ω

by using

Ω = argmax

Ω

p(Ω | y) = argmax

Ω

p(Ω,x,y)dx, (2)

and then estimating the original image by solving

x = argmax

p(x |

Ω,y). (3)

This inference procedure (called Evidence Analysis)

aims at optimizing a given function and not at obtain-

ing a posterior distribution that can be simulated to

obtain additional information on the quality of the es-

timates.

The calculation of p(Ω, x | y), however, may not

be possible, in which case we have to decide how to

approximateit. The Laplace approximation of distrib-

utions has been used, for instance, in blind deconvolu-

tion problemswhen the blur is partially known(Galat-

sanos et al., 2002; Galatsanos et al., 2000). An alter-

native method is provided by variational distribution

approximation. This approximation can be thought

of as being between the Laplace approximation and

sampling methods (Andrieu et al., 2003). The basic

underlying idea is to approximate p(Ω,x | y) with a

simpler distribution, usually one which assumes that

x and the hyperparameters are independent given the

data (see chapter II in (Beal, 2003) for an excellent

introduction to variational methods and their relation-

ships to other inference approaches).

The last few years have seen a growing inter-

est in the application of variational methods (Likas

and Galatsanos, 2004; Miskin, 2000; Molina et al.,

2006) to inference problems. These methods attempt

to approximate posterior distributions with the use of

the Kullback-Leibler cross-entropy (Kullback, 1959).

Application of variational methods to Bayesian infer-

ence problems include graphical models and neuronal

networks (Jordan et al., 1998), independent compo-

nent analysis (Miskin, 2000), mixture of factor ana-

lyzers, linear dynamic systems, hidden Markov mod-

els (Beal, 2003), support vector machines (Bishop

and Tipping, 2000) and blind deconvolution problems

(Miskin and MacKay, 2000; Likas and Galatsanos,

2004; Molina et al., 2006).

3 HYPERPRIORS, PRIORS AND

OBSERVATION MODELS

For emission tomography the conditional distribution

of the observed data y given x has the form

p(y | x) ∝

∏

i=1

exp{−

∑

j=1

i, j

}(

∑

j=1

i, j

)

, (4)

where A

i, j

is the contribution of the jth element of x

to the ith element of y. The system matrix A, with

elements A

i, j

, i = 1,...,M, j = 1, ..., N depends on

the geometry of the gamma camera and effects, such

as, the photon attenuation and the scatter contribution.

This model together with the image model constitute

the ﬁrst stage of the hierarchical Bayesian modeling.

For the image to be estimated we use as prior

model

p(x | π,β, α) =

∏

j=1

∑

c=1

| β

,α

)

, (5)

where, for a given number of classes C, π denotes the

C-dimensional vector π = (π

,... ,π

) consisting ofC

mixing proportions (weights) which are positive and

satisfy the normalization constraint

∑

c=1

= 1, (6)

and α and β denote, respectively, the C-dimensional

vectors α = (α

,... ,α

), β = (β

,...,β

) satisfying

> 1 and β

> 0, ∀c. Each pair (α

,β

) deﬁnes for

x > 0 the gamma probability distribution

(x | β

,α

) =





Γ(α

)

−1

−(α

/β

. (7)

The mean, variance, and mode of this gamma dis-

tribution are given by

E[x] = β

Var[x] = β

/α

Mode[x] = β

(1− 1/α

(8)

The parameter β

plays the role of the mean of

cluster c while the pair β

, α

controls the variance of

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

166

the prior distribution. There are then two nice inter-

pretations of the parameter α

it controls the smooth-

ness of the reconstruction in class c and also mea-

sures the conﬁdence on the prior mean. This second

interpretation resembles the conﬁdence values on the

hyperprior parameters in image restoration problems

(see, for instance, (Molina et al., 1999; Galatsanos

et al., 2000; Galatsanos et al., 2002)). In this pa-

per, following the approach in (Hsiao et al., 2002) we

will not attempt to estimate α

and leave it as an user-

speciﬁed parameter.

The use of gamma priors in medical images was

introduced in (Lange et al., 1987). To our knowledge

the use of mixtures of gamma priors in medical imag-

ing was ﬁrst proposed in (Hsiao et al., 1998) for trans-

mission tomography.

We now proceed to introduce the prior distribution

(hyperprior) on the unknown parameters. We note

that the set of unknown parameters is given by

Ω =

ω = (π,β) = (π

,...,π

,β

,... ,β

) |

≥ 0 ∀c with

∑

= 1, and β

> 0,∀c

.(9)

Following the Bayesian paradigm we have to de-

ﬁne now the hyperprior distribution on Ω. We can use

the following distribution on the unknown hyperpara-

meters ω ∈ Ω,

p(ω) = p(π)p(β), (10)

where p(π) and p(β) are ﬂat (assigning the same prob-

ability to all elements) distributions. We can, how-

ever, include additional information on the mixing

weights by using as p(π) the C-variate Dirichlet dis-

tribution deﬁned by

p(π) = p(π

,... ,π

)

Γ(a

+ ·· · + a

)

Γ(a

)··· Γ(a

)

−1

···π

−1

, (11)

over π

≥ 0 ∀c, with

∑

= 1 and zero outside,

where the a

’s are all real and positive. We will re-

fer to a distribution having the density function given

in equation (11) as the C-variate Dirichlet distribu-

tion D(a

,... ,a

). A D(a

,... ,a

) distribution has

the following marginal means and variances,

E[π

] =

+ ·· · + a

Var[π

] =

+ ·· · + a

− a

)

+ ·· · + a

)

+ ·· · + a

+ 1)

c = 1, ...,C, (12)

(see (Wilks, 1962)). Note that if a

= ρl

, where

> 0, ∀c and ρ > 0, the mean of π

does not depend

on ρ, while ρ can be used to increase or decrease the

variance of π

We will assume that β

, c = 1, ...,C has as hyper-

prior distribution p(β

), the inverse gamma distribu-

tion deﬁned by

(β

| m

) =

((m

− 1)n

)

Γ(m

)

−m

−1

−(m

−1)n

/β

. (13)

where m

> 1 and n

> 0, ∀c, and the mean, variance,

and mode of this inverse gamma distribution are given

E[β

] = n

, Var[β

] = (n

)

/(m

− 2),

Mode[β

] = (m

− 1)n

/(m

+ 1). (14)

We now have a probability distribution deﬁned

over (π,β,x, y) which has the form

p(π,β,x,y) = p(π)p(β)p(x | π,β)p(y | x) (15)

4 BAYESIAN INFERENCE AND

VARIATIONAL

APPROXIMATION

In order to perform inference we need to either

calculate or approximate the posterior distribution

p(π,β,x | y). Since this posterior distribution can not

be found in closed form, we will apply variational

methods to approximate this distribution by the dis-

tribution q(π,β,x).

The variational criterion used to ﬁnd q(π,β,x)

is the minimization of the Kullback-Leibler diver-

gence, given by (Kullback and Leibler, 1951; Kull-

back, 1959)

(q(π,β,x) k p(π,β,x | y)) =

π,β,x

q(π,β,x)log



q(π,β,x)

p(π,β,x | y)



dπdβdx

π,β,x

q(π,β,x)log



q(π,β,x)

p(π,β,x,y)



dπdβdx

+logp(y), (16)

which is always non negative and equal to zero only

when q(π,β, x) = p(π,β,x | y).

We choose to approximate the posterior distribu-

tion p(π,β,x | y) by the distribution

q(π,β,x) = q(π)q(β)q(x), (17)

where q(π), q(β) and q(x) denote distributions on π,

β and x respectively. In the following we provide the

derivation of two approximations of the posterior dis-

tribution as well as their algorithmic descriptions.

VARIATIONAL POSTERIOR DISTRIBUTION APPROXIMATION IN BAYESIAN EMISSION TOMOGRAPHY

RECONSTRUCTION USING A GAMMA MIXTURE PRIOR

167

4.1 General Case

We now proceed to ﬁnd the best of these distributions

in the divergence sense.

Let

Φ = {π, β,x}. (18)

For θ ∈ Φ let us denote by Φ

the subset of Φ with

θ removed; for instance, if θ = x, Φ

= (π,β). Then,

Eq. (16) can be written as

(q(π,β,x) k p(π,β,x | y))

= C

(q(θ)q(Φ

) k p(π,β,x | y))

q(θ)



q(Φ

)log



q(θ)q(Φ

)

p(π,β,x,y)



dΦ



dθ

+const. (19)

Now, given q(Φ

) =

∏

ρ6=θ

q(ρ), (if, for instance,

θ = x then q(Φ

) = q(π)q(β)), an estimate of q(θ) is

obtained as

ˆq(θ)=argmin

q(θ)

(q(θ)q(Φ

)) k p(π,β, x | y)).

(20)

Thus, we have the following iterative procedure

to ﬁnd q(π,β,x).

Algorithm 1 General case. Iterative estimation of

q(π,β,x) = q(π)q(β)q(x).

Given q

(β), and q

(x), the initial estimates of the

distributions q(β), and q(x),

For k = 1,2,... until a stopping criterion is met:

1. Find

(π) =

argmin

q(π)

(q(π)q

(β)q

(x) k p(π, β,x | y)), (21)

2. Find

k+1

(β) =

argmin

q(β)

(π)q(β)q

(x) k p(π, β,x | y)), (22)

3. Find

k+1

(x) =

argmin

q(x)

(π)q

k+1

(β)q(x)kp(π,β,x| y))(23)

Set

q(π)= lim

k→∞

(π), q(β)= lim

k→∞

(β), q(x)= lim

k→∞

(x).

(24)

4.2 Degenerate Case

In the previous algorithm we have performed the

search of the distributions q(π), q(β), and q(x) in

an unrestricted manner. However, we can reduce the

space of search to the set of degenerate distributions.

This approach, to be developed now, will not provide

information on the quality of the estimates but we use

it to justify some of the estimation procedures pro-

posed in the literature as the solution of the variational

approach to posterior distributions when a particular

distribution approximation is used.

Let

A =



π=(π

,... ,π

) | π

≥ 0 ∀c with

∑



(25)

and

B = {β = (β

,... ,β

) | β

> 0 ∀c }. (26)

Instead of using an unrestricted search for the distrib-

ution of q(π), q(β), and q(x) we will here restrict our

search to the following sets of distributions

D(A) = {q(π) | q(π) is a degenerate

distribution on an element of A} (27)

D(B) = {q(β) | q(β) is a degenerate

distribution on an element of B} (28)

D((R

)

) = {q(x) | q(x) is a degenerate

distribution on an element of (R

)

},(29)

where a degenerate distribution takes one value with

probability one, that is,

q(θ) =



1 if θ = θ

0 otherwise

(30)

When q

(π), q

(β), and q

(x) are degenerate dis-

tributions, we will denote by π

, β

, and x

respec-

tively the values these distributions take with proba-

bility one. We will also use the subscript D on the

distributions q(·) to denote the degenerate approxi-

mations q

(·). Then, the variational approach when

using degenerate distributions becomes:

Algorithm 2 Degenerate case. Iterative estimation

of q

(π,β,x) = q

(π)q

(β)q

(x)

Given β

∈ B, and x

, the initial estimates of β and x,

respectively, for k = 1,2,. . . until a stopping criterion

is met:

1. Find

= argmin

π∈A

−logp(π, β

,y)

, (31)

2. Find

k+1

= argmin

β∈B

−logp(π

,β,x

,y)

, (32)

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

168

3. Find

k+1

= arg min

x∈(R

)

−logp(π

,β

k+1

,x,y)

(33)

Set

(π,β,x) =







1 if π=lim

k→∞

,β= lim

k→∞

x = lim

k→∞

0 elsewhere

(34)

Interestingly, this is the formulation used in (Hsiao

et al., 2002) to estimate the hyperparameters and the

image when ﬂat distributions on π and β are used.

4.3 Implementation

In order to ﬁnd the distributions solutions of algo-

rithms 1 and 2, we deﬁne two sets of positive weights

Λ = {λ = (λ

,...,λ

) | λ

= (λ

j,1

,...,λ

j,C

) satis-

ﬁes

∑

c=1

j,c

= 1, λ

j,c

≥ 0, c = 1,...,C}

and

ϒ = {µ = (µ

; j = 1...,N) | µ

= (µ

j,1

,...,µ

j,M

)

with

∑

j=1

j,i

= 1, ∀i µ

j,i

≥ 0, ∀i, j}

Then for λ ∈ Λ and µ ∈ ϒ we have

logp(π,β, x,y) = logp(π) + logp(β)

∑

log

∑

c=1

| β

,α

)

−

∑

i=1

∑

j=1

i, j

∑

i=1

y(i)log

∑

j=1

i, j

≥ logp(π) + logp(β)

∑

c=1

j,c

log



j,c

| β

,α

)



−

∑

i=1

∑

j=1

i, j

∑

i=1

y(i)

∑

j=1

j,i

log



i, j

j,i



= L(π,β,x,λ,µ) (35)

In consequence, for λ ∈ Λ and µ ∈ ϒ we have

−logp(π, β,x,y) ≤ −L(π,β, x,λ,µ) (36)

and

π β x

q(π,β,x)log



q(π,β,x)

p(π,β,x,y)



dπdβdx ≤

π β x

q(π,β,x)log



q(π,β,x)

exp[L(π,β,x,λ,µ)]



dπdβdx

This leads to the following procedure to ﬁnd the

distributions q(π,β, x) or q

(π,β,x). Note that we

are summarizing the non-degenerate and degenerate

cases in one algorithm.

Algorithm 3 Iterative estimation of q(π), q(β) and

q(x) or q

(π), q

(β) and q

(x).

Given q

(β), q

(x), or β

and x

and λ

∈ Λ and µ

∈

For k = 1,2,... until a stopping criterion is met:

1. Find the solution of

(π) = argmin

q(π)



π β x

q(π)q

(β)q

(x)

log



q(π)q

(β)q

(x)

exp[L(π,β,x,λ

,µ

)]



dxdβdπ



, (37)

which is given by

(π) = p

(π | a

∑

j=1

1,c

,... ,a

∑

j=1

1,C

(38)

or ﬁnd the solution of

= argmin

−L(π,β

,λ

,µ

)

(39)

which is given by

∑

j=1

j,c

+ a

− 1

∑

′

∑

j,c

′

∑

′

− 1)

c = 1,... ,C

(40)

2. Find the solution of

k+1

(β) = argmin

q(β)



β π x

(π)q(β)q

(x)

log



(π)q(β)q

(x)

exp[L(π,β,x,λ

,µ

)]



dxdπdβ



, (41)

which is given by

k+1

(β) =

∏

c=1

k+1

(β

) (42)

where

k+1

(β

) = p



| m

+ α

∑

j,c

+ α

∑

j,c

− 1)

∑

j,c

E[x

]

(x)

+(m

−1)n

+α

∑

j,c

−1



(43)

or ﬁnd the solution of

k+1

= argmin

−L(π

,β,x

,λ

,µ

)

(44)

which is given by

k+1

∑

j,c

+ (m

− 1)n

+ α

∑

j,c

c = 1, ...,C

(45)

VARIATIONAL POSTERIOR DISTRIBUTION APPROXIMATION IN BAYESIAN EMISSION TOMOGRAPHY

RECONSTRUCTION USING A GAMMA MIXTURE PRIOR

169

3. Find the solution of

k+1

(x) = argmin

q(x)



x β π

(π)q

k+1

(β)q(x)

log



(π)q

k+1

(β)q(x)

exp[L(π, β,x,λ

,µ

)]



dπdβdx



, (46)

which is given by

k+1

(x) =

∏

k+1

) (47)

where

k+1

) = p

| u

k+1

) (48)

and

k+1

∑

j,c

∑

y(i)µ

(49)

k+1

= u

k+1

∑

j,c





k+1

(β)

∑

i, j

(50)

or ﬁnd the solution of

k+1

= argmin

−L(π

,β

k+1

,x,λ

,µ

)

(51)

which is given by

k+1

= (u

k+1

− 1)/

∑

j,c

k+1

∑

i, j

(52)

4. Find the solution of

k+1

,µ

k+1

arg min

λ∈Λ,µ∈ϒ



π β x

(π)q

k+1

(β)q

k+1

(x)

log



(π)q

k+1

(β)q

k+1

(x)

exp[L(π, β,x,λ,µ)]



dπdβdx



, (53)

which is given by

k+1

j,c

=expE [log(π

|β

,α

))]

k+1

(x)q

k+1

(β)q

(π)

∑

′

expE [log(π

′

| β

′

,α

′

))]

k+1

(x)q

k+1

(β)q

(π)

c = 1,... ,C (54)

and

k+1

j,i

expE [logA

i, j

]

k+1

(x)

∑

′

expE



logA

i, j

′



(x)

j = 1,.. .,N

(55)

or ﬁnd the solution of

k+1

,µ

k+1

= arg min

λ∈Λ,µ∈ϒ

−L(π

,β

k+1

,λ,µ)

(56)

which is given by

k+1

j,c

k+1

| β

k+1

,α

)

∑

′

k+1

| β

k+1

′

,α

′

)

c = 1,... ,C

(57)

and

k+1

j,i

i, j

k+1

∑

′

i, j

′

k+1

′

j = 1,.. . ,N (58)

For the non-degenerate case set

q(π) = lim

k→∞

(π), q(β) = lim

k→∞

(β),

q(x) = lim

k→∞

(x) (59)

while for the degenerate case set

(π,β,x) =







1 if π= lim

k→∞

,β= lim

k→∞

x = lim

k→∞

0 elsewhere

(60)

E[x

]

(x)

, E[log(π

| β

,α

))]

k+1

(x),q

k+1

(β),q

(π)

E[1/β

]

k+1

(β)

and E[logA

i, j

]

k+1

(x)

are calculated

in the Appendix.

5 EXPERIMENTAL RESULTS

In order to evaluate the proposed method we have per-

formed a set of tests over a real thoracic SPECT study.

Emission images of a thorax present abrupt edges in

the transition between tissues, therefore the gamma

mixture prior is well adapted to the characteristics of

these images.

The detector system used is a Siemens Orbiter

6601. The detector described a circular orbit clock-

wise, at 5.625 steps (there are 64 angles, 64 bins, and

64 slices). The data givenby the detector system were

corrected for the attenuation effect.

We have centered our attention in a cross sectional

slice of the heart which presents a signiﬁcant struc-

ture. This cut corresponds to the inferior part of the

left ventricle of the heart and the superior area of the

liver.

In the experiments we use three classes (back-

ground, liver and ventricle). Very similar results

are obtained by the degenerate and non-degenerate

posterior distribution approximations. However, the

non-degenerate reconstructions are sharper and less

noisy. Thus, we only present the non-degenerate re-

sults here.

The initial values q

(β), q

(x), λ, and µ were esti-

mated from a C-mean clustering of the Filtered Back-

projection (FBP) reconstruction. The parameters α

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

170

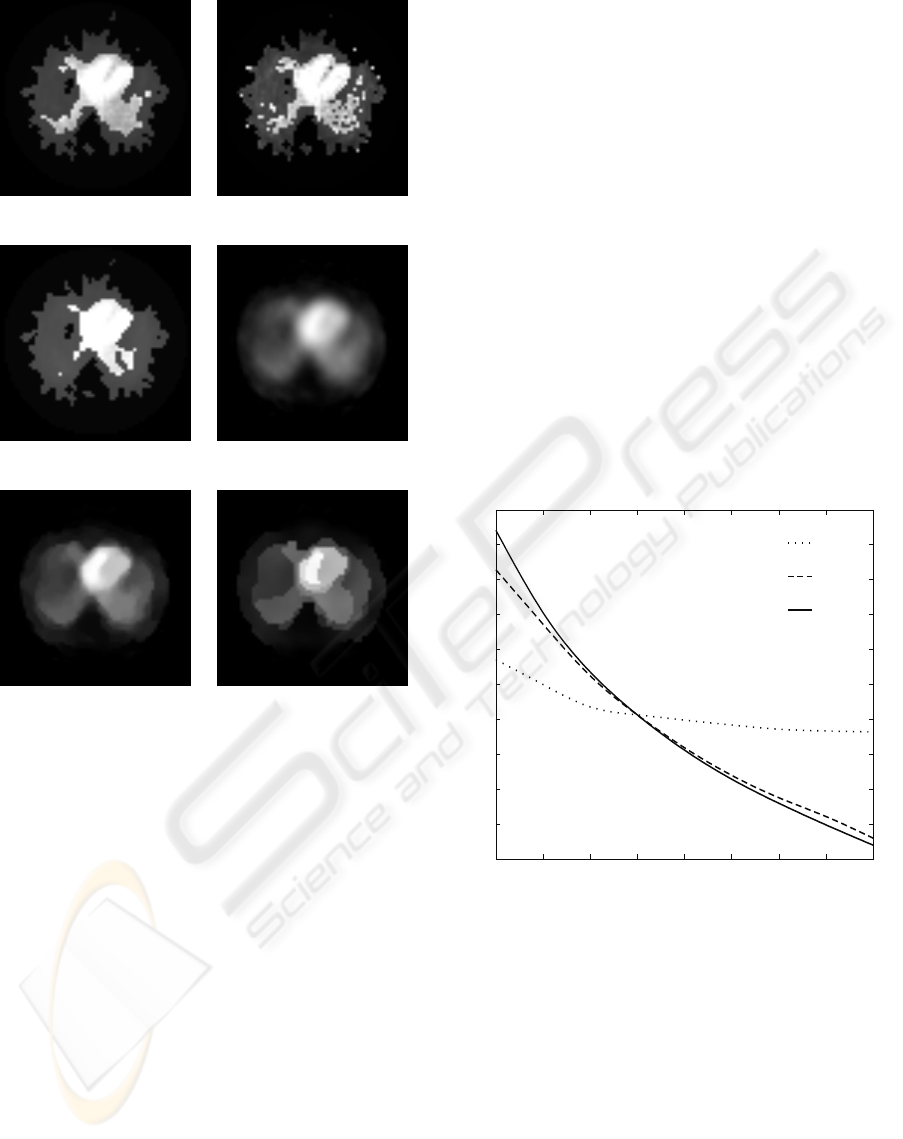
(a) α

= 60,α

= 10,α

= 10 (b) α

= α

= 10

= α

= 90 (d) CAR prior

(e) GGMRF prior (f) CGMRF prior

Figure 1: Results with SPECT image.

, and α

were selected experimentally to obtain an

acceptable visual tradeoffbetween detail and noise re-

duction. These parameters were equal to 60, 50, and

32, respectively. Figure 1(a) shows the reconstruction

obtained by the proposed method. The ventricle is

clear in the image and we can observe a small black

area in the left region of the image (possible tumor).

The patient presented a symptomatology compatible

with a hepatic tumor. Small values of α

produce very

noisy reconstructions (see Fig. 1(b)), while large val-

ues of α

cluster in excess the pixels of the recon-

structed image (see Fig. 1(c), where part of the my-

ocardial wall is not distinguishable).

The variances of the gamma distributions q(x

) =

q(x

| u

) provide information about the inﬂuence

of the α

’s on the reconstruction. These variances

are given by var[x

]

q(x

)

= v

. For our experi-

ment, Fig. 2 shows the dependence of the mean of the

above variances on α

, α

, and α

(we plot the curves

that correspond to each α

parameter with ﬁxed val-

ues for the other two parameters). We can observe

that the value of α

(background and tumor) is not es-

pecially critical for the reconstruction while we need

a more careful selection of the parameters α

(liver)

and α

(ventricle).

For visual comparison, since the original image is

obviously not available, we show the obtained recon-

struction using several image priors: conditional au-

torregresive (CAR), generalized Gauss Markov ran-

dom ﬁelds (GGMRF) and compound Gauss Markov

random ﬁeld (CGMRF) (see Figs. 1(d), 1(e) and

1(f)), respectively). These reconstructions were ob-

tained with the proposed methods in (L´opez et al.,

2004; L´opez et al., 2002) The area of the tumor is

clearer in the image provided by the reconstruction

using a gamma mixture prior. For example, the lesion

zone does not appear in the obtained reconstruction

with the CGMRF prior (see Fig. 1(f)). We note that in

the proposed method the isotope activity is homoge-

neous in the left ventricle, but it is not homogeneous

in the reconstruction obtained by using the other pri-

ors.

10 20 30 40 50 60 70 80 90

var

Figure 2: Mean of var[x] with respect to α

6 CONCLUSION

We present a reconstruction method for emission

computed tomography which uses a gamma mixture

as prior distribution to reconstruct Nuclear Medicine

images that present abrupt changes of activity be-

tween contiguous tissues, since spatially independent

priors, as the gamma mixture, are more adapted to this

type of images. We use variational methods to obtain

the original image and parameters estimation within

an uniﬁed framework. Satisfactory experimental re-

VARIATIONAL POSTERIOR DISTRIBUTION APPROXIMATION IN BAYESIAN EMISSION TOMOGRAPHY

RECONSTRUCTION USING A GAMMA MIXTURE PRIOR

171

sults are obtained with real clinical images.

ACKNOWLEDGEMENTS

This work has been partially supported by FIS

projects PI04/0857, PI05/1953 and by the Greece-

Spain Integrated Action HG2004-0014.

REFERENCES

Andrieu, C., de Freitras, N., Doucet, A., and Jordan, M.

(2003). An introduction to MCMC for machine learn-

ing. Machine Learning, 50:5–43.

Beal, M. (2003). Variational algorithms for approximate

Bayesian inference. PhD thesis, The Gatsby Compu-

tational Neuroscience Unit, University College Lon-

don.

Bishop, C. and Tipping, M. (2000). Variational relevance

vector machine. In Proceedings of the 16th Confer-

ence on Uncertainty in Articial Intelligence, pages

46–53. Morgan Kaufmann Publishers.

Galatsanos, N. P., Mesarovic, V. Z., Molina, R., and Kat-

saggelos, A. K. (2000). Hierarchical bayesian image

restoration for partially-known blur. IEEE Trans Im-

age Process, 9(10):1784–1797.

Galatsanos, N. P., Mesarovic, V. Z., Molina, R., Katsagge-

los, A. K., and Mateos, J. (2002). Hyperparameter es-

timation in image restoration problems with partially-

known blurs. Optical Eng., 41(8):1845–1854.

Hsiao, I.-T., Rangarajan, A., and Gini, G. (1998). Joint-map

reconstruction/segmentation for transmission tomog-

raphy using mixture-models as priors. In Proceed-

ings of EEE Nuclear Science Symposium and Medical

Imaging Conference, volume II, pages 1689–1693.

Hsiao, I.-T., Rangarajan, A., and Gini, G. (2002). Joint-map

Bayesian tomographic reconstruction with a gamma-

mixture prior. IEEE Trans Image Process, 11:1466–

1477.

Jordan, M. I., Ghahramani, Z., Jaakola, T. S., and Saul,

L. K. (1998). An introduction to variational meth-

ods for graphical models. In Learning in Graphical

Models, pages 105–162. MIT Press.

Kullback, S. (1959). Information Theory and Statistics.

New York, Dover Publications.

Kullback, S. and Leibler, R. A. (1951). On information and

sufﬁciency. Annals of Mathematical Statistics, 22:79–

86.

Lange, K., Bahn, M., and Little, R. (1987). A theoreti-

cal study of some maximum likelihood algorithms for

emission and transmission tomography. IEEE Trans

Med Imag, 6:106–114.

Likas, A. C. and Galatsanos, N. P. (2004). A variational ap-

proach for Bayesian blind image deconvolution. ieee

j sp, 52(8):2222–2233.

L´opez, A., Molina, R., Katsaggelos, A. K., Rodriguez, A.,

L´opez, J. M., and Llamas, J. M. (2004). Parameter es-

timation in bayesian reconstruction of SPECT images:

An aid in nuclear medicine diagnosis. Int J Imaging

Syst Technol, 14:21–27.

L´opez, A., Molina, R., Mateos, J., and Katsaggelos, A. K.

(2002). SPECT image reconstruction using com-

pound prior models. Int J Pattern Recognit Artif Intell,

16:317–330.

Miskin, J. (2000). Ensemble Learning for Indepen-

dent Component Analysis. PhD thesis, Astrophysics

Group, University of Cambridge.

Miskin, J. W. and MacKay, D. J. C. (2000). Ensemble learn-

ing for blind image separation and deconvolution. In

Girolami, M., editor, Advances in Independent Com-

ponent Analysis. Springer-Verlag.

Mohammad-Djafari, A. (1995). A full bayesian approach

for inverse problems. In in Maximum Entropy and

Bayesian Methods, Kluwer Academic Publishers, K.

Hanson and R.N. Silver eds. (MaxEnt95).

Mohammad-Djafari, A. (1996). Joint estimation of para-

meters and hyperparameters in a bayesian approach

of solving inverse problems. In Proceedings of the

International Conference on Image Processing, pages

473–477.

Molina, R., Katsaggelos, A. K., and Mateos, J. (1999).

Bayesian and regularization methods for hyperpara-

meter estimation in image restoration. IEEE Trans

Image Process, 8(2):231–246.

Molina, R., Mateos, J., and Katsaggelos, A. K. (2006).

Blind deconvolution using a variational approach to

parameter, image, and blur estimation. IEEE Trans

Image Process, 15(12):3715–3727.

Wilks, S. S. (1962). Mathematical Statistics. John Wiley

and Sons.

APPENDIX

In algorithm 3 we need to calculate the quantities

E[x

]

(x)

, E[log(π

| β

,α

))]

k+1

(x),q

k+1

(β),q

(π)

E[1/β

]

k+1

(β)

and E[logA

i, j

]

k+1

(x)

To calculate E[x

]

(x)

we note that (see Eq. 8)

E[x

]

)

= v

(61)

To calculate E[1/β

]

k+1

(β)

we observe with the use of

Eq. 13 that





q(β

)

((r

− 1)s

)

Γ(r

)

−(r

+1)−1

−(r

−1)s

/β

dβ

((r

−1)s

)

Γ(r

)

Γ(r

+ 1)

((r

−1)s

)

−1)s

(62)

VISAPP 2007 - International Conference on Computer Vision Theory and Applications

172

We can easily calculate E[logA

i, j

]

k+1

(x)

, since

E[logx

]

)

= −log

∂logΓ(u)

∂u

u=u

(63)

where

Γ(u) =

∞

u−1

−τ

dτ. (64)

(see (Miskin, 2000)). ∂logΓ(u)/∂u is the so called ψ

or digamma function.

To calculate the expectation E[log(π

,α

))]

k+1

(x),q

k+1

(β),q

(π)

we note that

E[log(π

| β

,α

))]

k+1

(x),q

k+1

(β),q

(π)

= E[logπ

]

(π)

+ α

logα

− α

E[logβ

]

k+1

(β)

−logΓ(α

) + (α

− 1)E[log(x)]

k+1

(x)

−α

]

k+1

(β)

E[x

]

k+1

(x)

(65)

where E[logπ

]

(π)

can be calculated taking into ac-

count that

E[logπ

]

(π

|ω,...,ω

)

∂logΓ(ω)

∂ω

ω=ω

−

∂logΓ(ω)

∂ω

ω=

∑

′

(66)

and E[logβ

]

k+1

(β

)

can be calculated observing that

follows a distribution p

(ρ

| m

,1/n

) and since

E[logβ

]

(β

)

= −E[logρ

]

(ρ

,1/n

)

(67)

which can be calculated using Eq. 63.

VARIATIONAL POSTERIOR DISTRIBUTION APPROXIMATION IN BAYESIAN EMISSION TOMOGRAPHY

RECONSTRUCTION USING A GAMMA MIXTURE PRIOR

173