Fourier Signature in Log-Polar Images

A. Gasperin, C. Ardito, E. Grisan and E. Menegatti

Intelligent Autonomous Systems Laboratory (IAS-Lab)

Department of Information Engineering

Via Gradenigo 6/b, 35131 Padova, Italy

Abstract. In image-based robot navigation, the robot localises itself by compar-

ing images taken at its current position with a set of reference images stored in

its memory. The problem is then reduced to ﬁnd a suitable metric to compare im-

ages, and then to store and compare efﬁciently a set of images that grows quickly

as the environment widen. The coupling of omnidirectional image with Fourier-

signature has been previously proved to be a viable framework for image-based

localization task, both with regard to data reduction and to image comparison.

In this paper, we investigate the possibility of using a space variant camera, with

the photosensitive elements organised in a log polar layout, thus resembling the

organization of the primate retina. We show that an omnidirectional camera us-

ing this retinal camera, provides a further data compression and excellent image

comparison capability, even with very few components in the Fourier signature.

1 Introduction

A mobile robot that moves from place to place in a large scale environment needs to

know its position in the environment to successfully plan its path and its movements.

The general approach to this problem is to provide the robot with a detailed descrip-

tion of the environment (usually a geometrical map) and to use some kind of sensors

mounted on the robot to locate in its world representation. Unfortunately, the sensors

used by the robots are noisy, and they are easily misled by the complexity of the en-

vironment. Nevertheless, several works successfully addressed this solution using high

precision sensors like laser range scanners combined with very robust uncertainty man-

agement systems [13] [2]. Another solution, very popular in real-life robot applications,

is the management of the environment. If artiﬁcial landmarks, such as stripes or reﬂect-

ing dots, are added to the environment, the robot can use these objects, which are easy

to spot and locate, to calculate its position on a geometrical map. An example of a

successful application of this method is the work of Hu [6]. Unfortunately, these two

approaches are not always feasible. There are situations in which an exact map of the

environment is either unavailable or useless for example, in old or unexplored build-

ings or in environments in which the conﬁguration of objects in the space changes fre-

quently. So, the robot needs to build its own representations of the world. This means

that in most cases a geometrical map contains more information than that needed by

the robot to move in the environment. Often, this adds unnecessary complexity to the

map building problem. In addition to the capability of reasoning about the environment

Gasperin A., Ardito C., Grisan E. and Menegatti E. (2007).

Fourier Signature in Log-Polar Images.

In Robot Vision, pages 87-96

DOI: 10.5220/0002070100870096

 SciTePress

topology and geometry, humans show a capability for recalling memorised scenes that

help themselves to navigate. This implies that humans have a sort of visual memory

that can help them locate themselves in a large environment. There is also experimental

evidence to suggest that very simple animals like bees and ants use visual memory to

move in very large environments [3]. From these considerations, a new approach to the

navigation and localization problem developed, namely, image-based navigation. The

robotic agent is provided with a set of views of the environment taken at various loca-

tions. These locations are called reference locations because the robot will refer to them

to locate itself in the environment. The corresponding images are called reference im-

ages. When the robot moves in the environment, it can compare the current view with

the reference images stored in its visual memory. When the robot ﬁnds which one of

the reference images is more similar to the current view, it can infer its position in the

environment. If the reference positions are organised in a metrical map, an approximate

geometrical localization can be derived. With this technique, the problem of ﬁnding the

position of the robot in the environment is reduced to the problem of ﬁnding the best

match for the current image among the reference images. The problem now is how to

store and to compare the reference images, which for a wide environment can be a large

number. In order to store and match a large number of images efﬁciently, it has been

shown in [9] the transformation of omnidirectional views into a compact representa-

tion by expanding it into its Fourier series. The agent memorises each view by storing

the Fourier coefﬁcients of the low frequency components. This drastically reduces the

amount of memory required to store a view at a reference location. Matching the current

view against the visual memory is computationally inexpensive with this approach.

We show that a further reduction in memory requirements and computations can be

met by using log-polar images, obtained by a retina-like sensor, without any loss in the

discriminatory power of the methods.

2 Materials

2.1 Omnidirectional Retinal Sensor

The retina-like sensor used in this work is the Giotto camera developed by Lira-Lab at

the University of Genova [11] [12] and by the Unitek Consortium [4]. It is built using

the 35µm CMOS technology, and arranging the photosensitive elements in a log-polar

geometry. A constant number of elements is placed on concentric rings, so that the size

of these elements necessarily decreases from the periphery toward the center. This kind

of geometric arrangement has a singularity in the origin, where the element dimension

would shrink to zero. Since this dimension is constrained by the building technology

used, there is a ring from which no dimension decrement is possible for accomodat-

ing a constant number sensitive elements. Hence, the area inside this limiting ring does

not show a log-polar geometry in the arrangement of the elements, but is nevertheless

designed to preserve the polar structure of the sensor and at the same time tessellate

the area with pixels of the same size. This internal region will be called the fovea of

the sensor for its analogy with the fovea in the animal retina, whereas the region with

constant number of pixels per ring will be called periphery.

The periphery is composed by N

per

= 110 rings with M = 252 pixels each, and the

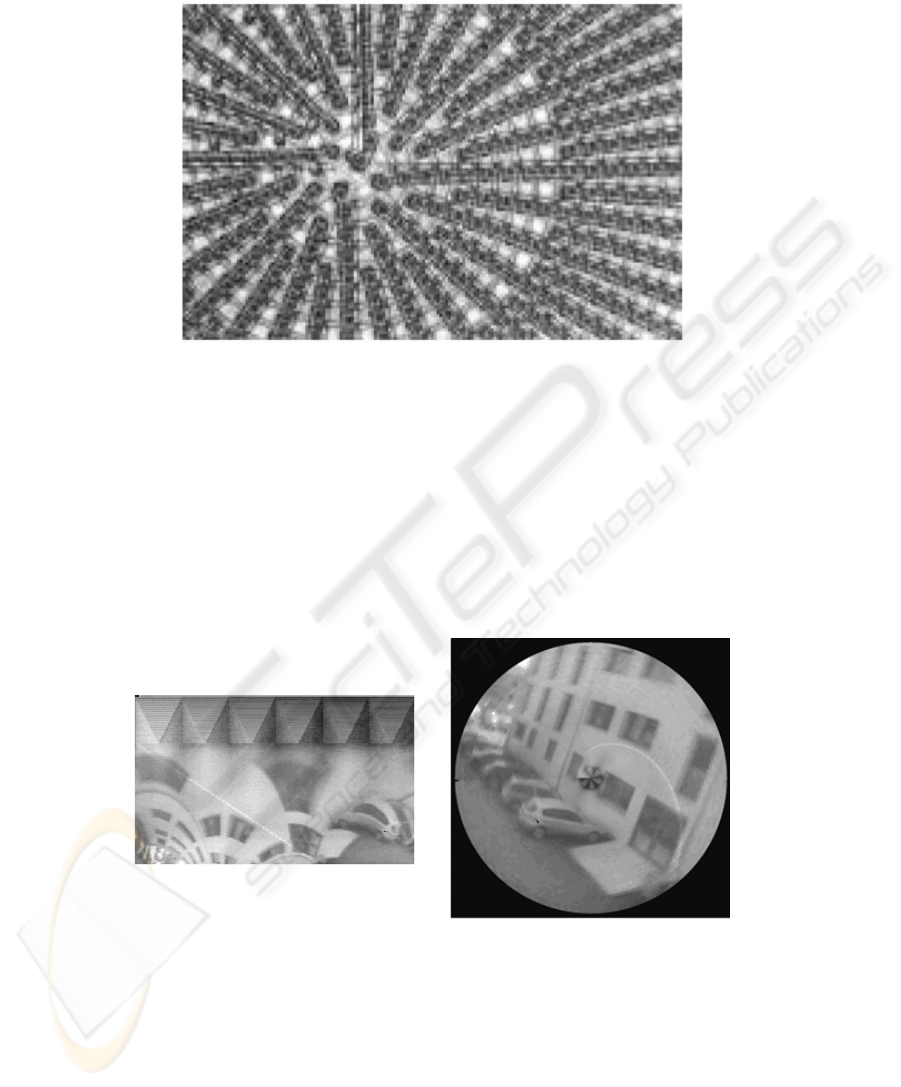
Fig.1. The central part of the electronic layout of the retinal sensor (from [4]).

fovea is composed by N

f ov

= 42 rings (see Fig. 1). This lead to a log-polar image hav-

ing size of MxN = 252x152, where N = (N

per

+ N

f ov

), and the image is obtained

from a sensor with 38.304 photosensitive elements. It is claimed in [4] that given its

resolution, the log polar sensor yields an image equivalent to a 1090x1090 image ac-

quired with a usual CCD: a sample image acquired with this camera is shown in Fig. 2,

together with its cartesianig:retina remapping in Fig. 3

Fig.2. A sample 252x152 image acquired

with the retina-like camera.

Fig.3. The sample image of Fig. 2 trans-

formed in a 1090x1090 cartesian image.

To obtain the omnidirectional sensor, the retina-like camera is coupled with an hy-

perbolic mirror with a black needle at the apex of the mirror to avoid internal reﬂections

on the glass cylinder [7]: the sensor can be seen in Fig. 4(a). A single omnidirectional

image gives a 360

view of the environment, as can be seen in Fig. 4(b).

(a) (b)

Fig.4. (a) The omnidirectional sensor composed by the retina-like camera and the hyperbolic

mirror. (b) A sample image acquired with the omnidirectional retinal sensor.

3 Methods

3.1 Log-Polar Omnidirectional Image

The pixel coordinates of the output image of the retinal sensor are polar coordinates

(ρ, ϑ), that are related to the usual cartesian coordinates (x, y) via:

ρ = log



+ y



ϑ = arctan





(1)

There are two main issues to be considered while dealing with log-polar images. The

ﬁrst is that there is a singularity in the transformation near the origin, where the pixel

dimension tend to zero. The transformation can thus be considered exact only in the re-

gion outside the fovea, whereas inside the fovea the mapping depends on the particular

arrangement of the retinal sensor.

The second point is the consideration that given the sampling in polar coordinates in-

duced by the sensor, moving from the center toward the periphery of the image, the

mapping is not bijective from (ρ

, ϑ

) → (x

, y

), but rather one point in the log polar

image correspond to a sector of annular ring:

(ρ

, ϑ

) → {(x, y)|ρ ∈ [ρ

, ρ

i+1

[ ∩ ϑ ∈ [ϑ

, ϑ

i+1

[} (2)

This means that from the center of the image toward its outer boundary, the resolution

decreases, as a pixel in the log-polar image gather information from a bigger area than

a pixel, e.g., in the fovea.

An interesting property of the retinal sensor appears when it is coupled with an hyper-

bolic mirror,so to provide an omnidirectional sensor.In fact the space-variant resolution

of the sensor, if matched with the hyperbolic projection provide an omnidirectional im-

age of nearly constant resolution. Moreover,the image acquired by this omnidirectional

sensor is already in the form of a panoramic cylinder, without need of further transfor-

mations [12,10].

3.2 Fourier Signature

In image-based navigation the main problem is the storage of reference images and

the comparison of these images with those acquired during the localization. In [9] was

shown the effectiveness of using a small number of Fourier coefﬁcients to characterize

an image: that method both reduce drastically the dimension of the information to be

stored and proved to be enough to discriminate different images, without the need of

image alignment as in [1] [5] [8].

The Fourier signature is computed in two steps. First, we calculate the 1-D Fourier

transform of every line of the log-polar image and we store in a matrix the Fourier

coefﬁcients line by line. Then, we keep only a subset of the Fourier coefﬁcients, those

corresponding to the lower spatial frequencies, as signature for the image.

To fully exploit the further dimensionality reduction imposed by the retina-like sensor,

we have to recall that in the fovea the effectivephysical pixels (and therefore the amount

of information) is 1 in the center, that is mapped in ﬁrst line of the log-polar image, 4

in the second innermost ring, mapped in the second line, and so on until the number

of pixels in the ring match that of the periphery, where the amount of pixels per ring is

constant. A number of physical pixels smaller than the number of image pixels induces

a smaller band on the signal than it would be possible given the image dimension.

This leads to the consideration that in the foveal region we need to retain less Fourier

coefﬁcients than in the periphery to achieve a storage efﬁciency without loosing any

information. The choice is therefore to decrease linearly the number of coefﬁcients

used to build the signature: from the k

max

per line in the periphery (rows N

f ov

+ 1 to

N in the log-polar image), to the 1 coefﬁcient of the ﬁrst line of the image. Hence for

the row y:

k(y) =

(

⌈

max

−1

fov

−1

· y +

max

−N

fov

max

−1

⌉ if y ≤ N

f ov

max

if y > N

f ov

(3)

with ⌈x⌉ meaning the ceiling of x.

3.3 Dissimilarity Measure

Given an image I, and the discrete set of its Fourier coefﬁcients for the line y, a

y,k

with y = 1, . . . , N, we can deﬁne the Fourier signature as the vector F containing the

juxtaposition of all Fourier coefﬁcients of the signature for each line:

F(I) =



1,1

, . . . , a

1,k(1)

, . . . , a

N,1

, . . . , a

N,k(N)



(4)

A distance between two images I

and I

can be evaluated as the L

norm between the

two vectors of their Fourier signature:

d(I

, I

) = |F(I

) − F(I

(5)

When a database of images is available, and a new image have to be compared with

those in the database to ﬁnd the best match, is often more intuitive to use a measure of

relative distance of the image under examination from one in the database, given all the

images in the database:

p(I

, I

) = 1 −

d(I

, I

)

max

i,j

(d(I

, I

))

(6)

This is a normalized distance in the database, assuming values in the interval [0, 1], and

can therefore be viewed as a probability a posteriori of an image I

to be equal to image

, with j = 1, . . . , N, and N the number of images in the database.

4 Results and Discussion

To test the proposed measure, an image database was built by acquiring a frame from

different positions in an indoor environment, using the retinal omnidirectional camera

described previously. The acquisition sites were 15 locations 20cm apart.

First of all, we made experimentations to evaluate which is the minimum number of

Fourier coefﬁcients necessary to construct a Fourier signature that retains all and only

the necessary information. Hence, we calculated the similarity of each input image

against all the reference image of the dataset varying the number of coefﬁcients per row

max

) of the Fourier signature. Since the Nyquist frequency of each row is f

the maximum number of coefﬁcients of the DFT which yield effective information is

. Therefore, we made k

max

∈ K = [1, . . . ,

For each k

max

∈ K we ﬁrst evaluated the similarity measure Eq. (6) of each image

in the reference database from every other image in the reference database. By this

mean, we show that Eq. (6) is an effective measure to distinguish different images, and

can therefore be used to provide a good localization performance in autonomous robot

navigation tasks. In Fig. 7 we show three successive sample images (relative distance

equal to 15cm) from the reference database, and the similarity value of an input image

taken at a location corresponding to the second reference image. The similarity value

yields a correct match between input and reference.

In Fig. 5 and Fig. 6, it is shown the values of the similarity value for different values

of k

max

of an image in the reference database with every other image. In both ﬁgures,

the similarity peak corresponds to the correct image, and the similarity values decrease

around the peak, the higher k

max

, the sharper the decrease.

The choice of k

max

inﬂuences the trade off between dissimilarity accuracy and image

storage efﬁciency. A good measure of the accuracy of the proposed measure is the mini-

mum differencebetween 1−d(I

, I

) for i 6= j. This is equivalent to evaluate a classiﬁer

2 4 6 8 10 12 14

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Images

Similarity Value

1 Fourier Coefficient per Row

63 Fourier Coefficients per Row

126 Fourier Coefficients per Row

Fig.5. Similarity measure p(I

, I

) for j = 1, . . . , N, for k

max

= 1, 63, 126. It is clear that the

correct image always yields a similarity measure of 1, whereas the decreasing in the similarity is

sharper for high values of k

max

2 4 6 8 10 12 14

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Images

Similarity Value

1 Fourier Coefficient per Row

63 Fourier Coefficient per Row

126 Fourier Coefficients per Row

Fig.6. Similarity measure p(I

, I

) for j = 1, . . . , N , for k

max

= 1, 63, 126. It is clear that the

correct image always yields a similarity measure of 1, whereas the decreasing in the similarity is

sharper for high values of k

max

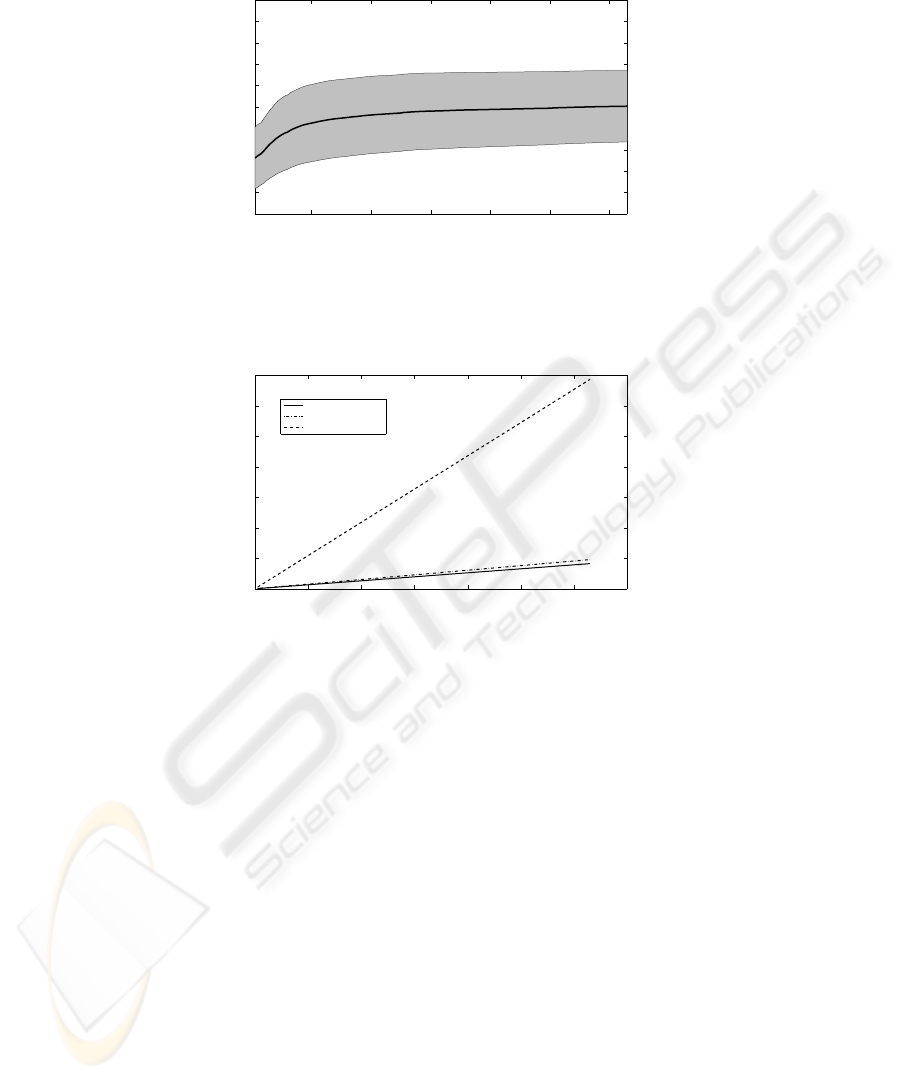
margin, in the separation between two different images. In Fig. 8, we show that after a

monotonic increase in this margin whith the number of coefﬁcients, it reaches a kind of

plateau after k

max

≃ 20.

The storage efﬁciency achieved is clear when comparing the number of Fourier

coefﬁcients needed to form the Fourier signature of a log-polar image with the number

of the equivalent cartesian image, which has dimension 1090x1090 pixels. In Fig. 9

we show for different k

ax the dimension of the Fourier signature for the equivalent

cartesian image, for the log-polar image with k

max

coefﬁcients per row, and for the log-

polar image with k(y) coefﬁcients per row, meaning that we have a reduced number of

coefﬁcients in the foveal rings. It is well apparent the storage reduction that can be

achieved using a retina-like sensor.

(a) Reference Image 1 (b) Reference Image 2

Fig.7. Three reference image taken 15 cm apart, to be confronted with an input image acquired

at location (b). With k

max

= 10, the similarity value of the input image with image (a) is 0.59,

with (b) is 0.96, and with (c) is 0.54: the correct match has the highest similarity value.

5 Conclusions

In this paper we show that retinal omnidirectional images can be successfully used

to localize an autonomous robot with the image-based navigation approach. Within

this approach, the direct comparison of images is not robust, is too computationally

cumbersome, and the storage of the whole images requires an excessive memory space.

Representing the images with their Fourier signature has been proved a viable way to

overcome these problems. In this paper, we showed that coupling this technique with

log-polar sensor yields a further dimensionality reduction with sufﬁcient accuracy.

The reduction is achieved by exploiting the different bandwidth of each ring of the

retina-like sensor with respect to the constant bandwidth of a cartesian sensor, where

each row contains the same number of photosensitive element. This allows to keep a

decreasing number of Fourier coefﬁcients in the signature, moving from the periphery

toward the center of the sensor.

Despite the storage requirement reduction, we show that using a simple L

norm on

difference of signature vectors have an excellent discriminatory power in distinguishing

images taken at different sites.

20 40 60 80 100 120

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Number of Coefficients per Row in the Fourier Signature

Minimum Dissimilarity Value

Fig.8. Minimum difference in the proposed similarity measure p(I

, I

) for every different im-

age in the database, and for k

max

= 1, . . . , 126. The solid line represent the mean minimum

difference µ, and the gray area represent the variability of this value µ ± σ.

0 20 40 60 80 100 120 140

x 10

max

Number of elements in the Fourier Signature

Foveal Coefficients Reduction

Equal k

max

for each Row

Equivalent Cartesian Image

Fig.9. Total number of coefﬁcients needed to form the proposed Fourier Signature, with respect

to k

max

Acknowledgements

We would like to thank Prof. G. Sandini and coworkers for having kindly provided the

retinal camera, of which only few prototypes exist.

This research has been partially supported by the Italian Ministry for Education and

Research (MIUR) and by the University of Padova (Italy).

References

1. H. A. ans N. Iwasa, N. Yokoya, and H. Takemura. Memory-based self-localisation using

omnidirectional images. In Proceedings of the 14th International Conference on Pattern

Recognition, volume 1, pages 1799–1803, 1998.

2. W. Burgard, D. Fox, M. Moors, R. Simmons, and S. Thrun. Collaborative multi-robot explo-

ration. In Proceedings of the IEEE International Conference on Robotics and Automation

(ICRA), 2000.

3. T. Collett, E. Dillmann, A. Giger, and R. Wehner. Visual landmarks and route following in

desert ants. Journal of Comparative Physiology A, 170:435–442, 1992.

4. Consorzio Unitek. Giotto : retina-like camera.

5. J. Gaspar, N. Winters, and J. Santos-Victor. Vision-based navigation and environmental rep-

resentations with an omnidirectional camera. IEEE Transactions on robotics and automa-

tion, 16(6):890–898, December 2000.

6. H. Hu and D. Gu. Landmark based localisation of industrial mobile robots. International

Journal of Industrial Robot, 27(6):458–467, November 2000.

7. H. Ishiguro. Development of low-cost compact omnidirectional vision. In R. Benosman and

S. B. Kang, editors, Panoramic Vision,, chapter 3. Springer, 2001.

8. B. J. A. Kroese, N. Vlassis, R. Bunschoten, and Y. Motomura. A probabilistic model for

appearance-based robot localization. Image and Vision Computing, 19(6):381–391, April

2001.

9. E. Menegatti, T. Maeda, and H. Ishiguro. Image-based memory for robot navigation using

properties of the omnidirectional images. Robotics and Autonomous Systems, 47(4):251–

267, July 2004.

10. T. Pajdla and H. Roth. Panoramic imaging with SVAVISCA camera - simulations and real-

ity. Ctu-cmp-2000-16, Center for machine perception - Czech Technical University, October

2000.

11. G. Sandini and G. Metta. Retina-like sensors: motivations, technology and applications.

2002.

12. G. Sandini, J. Santos-Victor, T. Pajdla, and F. Berton. OMNIVIEWS: direct omnidirectional

imaging based on a retina-like sensor. In Proceedings of IEEE Sensors 2002, June 12-14

2002.

13. S. Thrun, M. Beetz, M. Bennwitz, W. Burgard, A. B. Cremers, F. D. Fox, D. Haehnel,

C. Rosenberg, N. Roy, J. Schulte, and D. Schulz. Probabilistic algorithms and the interactive

museum tour-guide robot Minerva. International Journal of Robotics Research, 19:972–999,

2000.