A FAST INTERPOLATION METHOD TO REPRESENT THE BRDF

IN GLOBAL ILLUMINATION

Pierre Y. Chatelier

LAIC, Universit

e d’Auvergne, Aubi

ere, France

emy Malgouyres

LAIC, Universit

e d’Auvergne, Aubi

ere, France

Keywords:

Global illumination, BRDF, discrete representation, spherical harmonics, control-points, interpolation, rota-

tion.

Abstract:

Global illumination that simulates realistic lighting environments makes use of bidirectional reﬂectance dis-

tribution functions (BRDF). Such a function is a surface property, describing how light is re-emitted after

hitting this surface. The present paper details a representation of BRDF and radiance distributions, based

on control points, that aims at performance. It uses spherical triangles for interpolation, least square mean

or linear programming for optimal representation, and very fast rotation by precomputing control points re-

weightening. It has some more advantages for deforming an existing shape. This approach is compared to

Spherical Harmonics, and outperforms this last one.

1 INTRODUCTION

Global illumination that simulates realistic lighting

environments must be able to describe how light is

re-emitted after hitting the surface of an object, de-

pending on the optical properties of this surface: the

material properties. The Lambertian model is one of

the simplest: a fraction of light (depending on the

zenithal incidence) is isotropically re-emitted above

the surface. This is also known as the ideal diffuse

case. In this case, the material property is embedded

in a single factor, as a real number.

However, most objects, like mirrors, velvet, wet

surfaces. . . should not use such a simple model. First,

asymetric materials like velvet must take in account

not only the zenithal angle of an incoming ray, but

also the azimuthal orientation of the ray according to

the surface. Second, incoming light is anisotropically

re-emitted. This is particularly obvious for a perfect

mirror, which is said to be a perfect specular reﬂec-

tor. Implementing a material mixing up diffuse and

specular properties implies a way to represent spatial

anisotropy.

The notion of Bidirectional Reﬂectance Distri-

bution Function (BRDF), and radiance distribution,

is the common way to describe such a behaviour.

This paper describes the well known problem of

representing and using BRDFs (Neumann, 2001;

Rusinkiewicz, 1997; Rusinkiewicz, 1998). The re-

quired operations for using them in a global illumi-

nation solver are presented, and we show how they

are addressed with spherical harmonics. Then, we in-

troduce a fast interpolation method, designed to per-

form these operations with maximal performance and

a reasonable precision. Computational experiments

have been performed to compare this method with the

spherical harmonics.

2 USING A BRDF

2.1 Representation

A BRDF function is a function of two parameters:

the direction of incoming light, and the direction of

the outgoing ray for which we want to know the re-

emission. Each direction is in fact a two-dimensional

parameter, usually denoted by the two spherical an-

gles θ and φ, representing elevation and azimuth

(see Fig. 1), so that a BRDF is rather seen as a 4-

dimensional function . The returned value is the ratio,

Y. Chatelier P. and Malgouyres R. (2007).

A FAST INTERPOLATION METHOD TO REPRESENT THE BRDF IN GLOBAL ILLUMINATION.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 5-12

DOI: 10.5220/0002072100050012

 SciTePress

of the reﬂected (or transmitted) radiance in the given

outgoing direction, to the incoming energy ﬂux from

the incoming direction. The BRDF of an ideal-diffuse

surface is constant, while an ideal reﬂector can be rep-

resented by a Dirac delta function. A simple BRDF

may be stored as a mathematical function, but arbi-

trary BRDFs usually require a set of sample points

that have to be interpolated. Many representations for

BRDFs have been proposed in the computer graphics

literature (Ward, 1992; Ashikhmin and Shirley, 2000;

Kautz et al., 2002), generally based on a decompo-

sition on a basis of spherical functions, like spher-

ical harmonics or spherical wavelets (Schr

oder and

Sweldens, 1995; Koenderink et al., 1996).

2.2 Models and Instanciations: Brdf

and Radiance Distributions

By stating that we are using a BRDF to modelize light

re-emission, we are only describing how we handle

this material property. However, one must not for-

get that this material property is static and is different

from the effective emission that appears in each ele-

ment that constitutes the surface. Indeed, considering

the 3D scene for which we are computing global illu-

mination, it is usually discretized into several patches,

each patch behaving like a light emitter. Patches from

the same surface will share the same BRDF, that de-

scribes their behaviour. But the effective emission

varies from patch to patch, according to the quantity

of energy that each one is re-emitting, and that has

been computed by the global illumination algorithm.

This effective emission is the radiance distribution,

which is a function of one parameter: the outgoing

direction (see Fig. 2). Here again, it can be seen as a

two-dimensional spherical function on θ and φ. This

function is not known in advance, it is what is com-

puted by the global illumination algorithm. At ﬁrst,

only the light sources have non-zero radiance distri-

butions. Then, progressively, light propagates and hits

some patches, that affects their radiance distributions

according to their local BRDF. Solving the global il-

lumination problem means that BRDF are known 4-

dimensional functions, while radiance distributions

are the unknowns, 2-dimensional functions.

For the sake of performance, these two kind of

objects are usually represented with the same data

structures. Instead of encoding a 4-dimensional

function, the BRDF can be implemented as the

interpolation of 2-dimensional functions. That is

to say, f (θ

, φ

, θ

out

, φ

out

) is computed from some

,φ

(θ

out

, φ

out

). Hence, both BRDF and radiance

distributions can be represented by 2D spherical func-

tions, and we only need a way to encode efﬁciently

out

incoming

outgoing

Figure 1: Polar angles to

deﬁne a BRDF. θ is the

zenithal angle (elevation), φ

is the azimuthal angle (ori-

entation).

Figure 2: A radiance dis-

tribution is the response of

a BRDF for some incoming

light. This one has diffuse

and specular behaviour.

such data.

2.3 Operations

As it is stated in Section 2.2, managing radiance dis-

tributions requires to encode 2D spherical functions.

In order to use such data, we must ensure some op-

erations to be easy to perform on the representation.

These operations are querying value, scaling, adding,

and rotating the distributions. Since they are to be

performed very often, they must be very efﬁcient.

2.3.1 Querying Value

The radiance distribution of a scene element evolves

while this element receives light during global-

illumination iterative solving. We must be able to

query at any time the light leaving an element in a

particular direction. This can be done using a mathe-

matical model, which returns a value for some param-

eters. This can also be done with interpolation, which

tries to guess a value according to some neighbor-

hood. The Spherical Harmonics mathematical model

is described in Section 2.4. We propose in Section 3

of this paper an interpolating method.

2.3.2 Scaling and Adding

When some light hits a scene element, its local BRDF

is queried for the matching radiance distribution.

Then this distribution is scaled by the effective incom-

ing energy quantity, and added to the radiance distri-

bution already held by the element. See Figure 3 for

an illustration.

2.3.3 Rotating

Radiance distibutions returned by BRDF queries are

computed in a global system of coordinates. They

have to be rotated to be added to a scene element,

which uses a local system. Indeed, θ is related to the

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

querying

radiance

distribution

the distribution

is scaled

BRDF

scene element

with new radiance

distribution

scene element with

radiance distribution

+ incoming

adding

incoming

Figure 3: Scaling and adding radiance distribution.

normal vector of the surface, and the azimuthal angle

is meaningful if the surface has an orientation.

2.4 Common Solution

A common method to fulﬁll all previous requirements

is to use a decomposition of the radiance distribution

function on a basis of spherical functions. The basis

being known, the radiance distribution is just encoded

by a set of coefﬁcients. Adding and scaling distribu-

tions becomes as easy as adding and scaling the coef-

ﬁcients. Rotation is usually the stumbling block.

2.4.1 Spherical Harmonics

Spherical harmonics are a basis of functions that

suits very well at representing spherical 2D func-

tions (Franc¸ois X. Sillion and Claude Puech, 1994;

Kautz et al., 2002). The spherical harmonics basis is

denoted by Y

l,m

and a function f is decomposed with

l,m

coefﬁcients as

f (θ, φ) =

∞

∑

l=0

∑

m=−l

l,m

(θ, φ) (1)

The deﬁnition of Y

l,m

functions makes use of as-

sociated Legendre Polynomials P

l,m

(x) and a normal-

izing constant N

l,m

(x).

l,m

(θ, φ) =











l,m

(cosθ)cos(mφ) if m > 0

l,0

(cosθ)

√

2 if m = 0

l,m

l,−m

(cosθ)sin(−mφ) if m < 0

l,m

2l + 1

2π

(l −|m|)!

(l + |m|)!

l,m

(x) =











(1 −2m)

√

1 −x

m−1,m−1

(x) (l = m)

x(2m + 1)P

m,m

(l = m + 1)

2l−1

l−m

l−1,m

(x) −

l+m−1

l−m

l−2,m

(x) (otherw.)

2.4.2 Cost of the Representation

The representation with spherical harmonics requires

to decide how many coefﬁcients are kept for the de-

composition. Since BRDF are usually rather smooth,

only a few dozens coefﬁcients will be needed. it is

important to keep this number the smallest possible,

because since each scene element will hold a whole

set of coefﬁcients, memory becomes rapidly a criti-

cal resource. A good balance must be found between

the expected precision and the required number of co-

efﬁcients (see Fig. 4). For a real function, only real

coefﬁcients are needed.

Ideal specular reﬂectors are typical examples of

failure of the assertion about smooth BRDFs. How-

ever, such reﬂectance should not be handled by a very

high frequency distribution, but algorithmically (Sil-

lion et al., 1991).

(a) (b)

(c)

Figure 4: (a) A spherical shape that is to be approximated.

It is made of a sphere with some stretchings. (b) Spheri-

cal harmonics, 16 coefﬁcients (dotted shape). This is not

enough to approximate the shape. ( c) Spherical harmonics,

64 real coefﬁcients (dotted shape). This is a good approxi-

mation of the spherical shape.

2.4.3 Rotation with Spherical Harmonics

The rotation with spherical harmonics is known to be

the stumbling block of this representation (K

riv

anek

et al., 2005). It is proved to be a linear opera-

tion (

Ohrstr

om, ; Blanco et al., 1997), by multiply-

ing the vector of coefﬁcients by a particular matrix.

A FAST INTERPOLATION METHOD TO REPRESENT THE BRDF IN GLOBAL ILLUMINATION

However, such a matrix may be unpractical in the cir-

cumstances (Erdelyi, 1953).

3 CONTROL-POINTS BASED

BRDF

In order to achieve maximal performance, we propose

a method based on interpolation on spherical trian-

gles. This method requires a reasonable amount of co-

efﬁcients, is precise enough for smooth radiance dis-

tributions, achieves very good performance for com-

mon operations, and suits very well for a direction-

based global illumination solver.

3.1 Interpolation

This simplest way to represent a spherical 2D func-

tion is to sample it on some points. If the polar angles

of these points are ﬁxed, the representation only needs

to store the radius component of the spherical coordi-

nates of these points. Then, two difﬁculties must be

adressed: choose the set of control points, and choose

an interpolation algorithm.

3.1.1 Choosing the Control Points

The control points must be chosen regularly on the

sphere, so that no region is arbitrarily ﬁner than an-

other. Once dispatched on the sphere, the control

points are radially translated to represent spherical

shapes. A good method to achieve this repartition is to

recursively subdivide a regular polyhedron (Schr

oder

and Sweldens, 1995). For instance, starting from a

icosahedron (12 vertices), one can take the middle of

each edge to divide each face into four new triangles.

The initial polyhedron is an important parameter

for the number of control points you wish to have.

With an icosahedron, the number of points grows

rapidly. At orders 0, 1, 2, 3 of subdivisions, this num-

ber is respectively 12, 42, 162, 642 (Fig. 5 and 6).

As stated in section 2.4.2, each scene element holds

a whole set of coefﬁcients, so that its cardinal should

be kept as small as possible, while being big enough

to allow precise radiance distributions. Our experi-

ments has shown that 162 points are a good compro-

mise (Fig 7). On these pictures, the dots are not the

control points, but some samples interpolated by our

method, using the control points.

3.1.2 Weightening

By subdivising as described above, we can deﬁne how

a point is interpolated by the control points.

Figure 5: Icosahedron (or-

der 0 of subdivisions).

Figure 6: Starting with

icosahedron, order 1 of

subdivisions.

(a) (b)

(c)

Figure 7: (a) A spherical shape that is to be approximated.

It is made of a sphere with some stretchings. (b) 42 control

points are used. The result is clearly not precise enough

to approximate the given shape. (c) 162 control points are

used. This is a good approximation of the spherical shape.

Let P be a point to be interpolated. If we project P,

and the control points, on the unit sphere, then the

projection P

of P falls into a spherical triangle made

by three of the projected control points on the sphere.

can also lie on an edge or a vertex in degenerated

cases, but this is not a problem.

Instead of using classical bi-linear interpolation, that

is useful for rasterized triangles in computer graphics,

we can instead weighten the vertices by the ratio of

the triangles areas deﬁned by P

and the control points

of the neighborhood. These triangles are spherical tri-

angles and their area is easy to compute with respect

to the formula:

area(ABC) =

A +

B +

C −π (2)

where

C are the angles at the vertices.

Let P be the point to be interpolated, its projection P

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

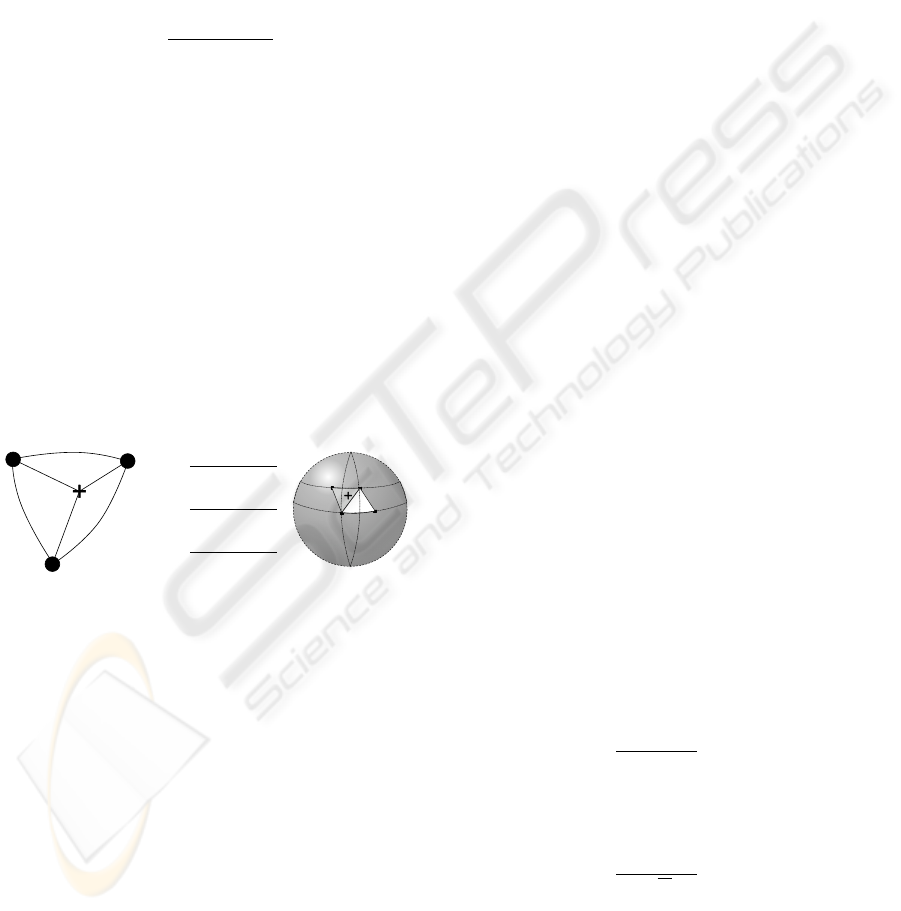
falling into the spherical triangle deﬁned by the pro-

jections C

, C

of the control points C

, C

and C

We denote the interpolation by writing

P = ω

+ ω

(3)

the unknowns being the weights ω

These weights can be computed according to the areas

of the spherical triangles formed by the projections.

Let these triangles be denoted by P

, P

, their areas being respectively α

, α

We can set

+ α

(4)

to get a normalized weightening system (Figure 8a).

3.1.3 Finding the Triangle

To determine the three control points to be used in

interpolation, we have to quickly compute in which

triangle a point is falling. If we are given the po-

lar angles of this point, it is easy to determine some

possible triangles where it is projected. This only re-

quires the control points to be sorted by parallels and

meridians. Once we have found the two parallels en-

cloising the projected point, we can determine which

neighbour control points on these parallels surround

the projection. Most of the time, more than one tri-

angle are candidate, but some cross products can then

determine easily which is the good one (Figure 8b).

+ α

(a) (b)

Figure 8: (a) Interpolation on spherical triangles. The

weights w

are determined from the areas α

. (b) The par-

allel and meridians of the control points help ﬁnding candi-

dates holding the projection.

3.2 Representing an Existing Function

We explained in Section 2.2 that even 4D-BRDFs

are modelized using 2D-spherical functions, unify-

ing BRDF and radiance distributions representations.

Therefore, we must provide an efﬁcient way to ap-

proximate a given 2D function, by ﬁnding an optimal

set of control points regarding the interpolation algo-

rithm.

To ﬁnd such an optimal set, we can solve the prob-

lem using Least-Squares Method, or Linear Program-

ming. Let f be the 2D spherical function to inter-

polate, and P

, θ

, φ

), i ∈ [0; n] the samples of this

function. Let C

, θ

, φ

), i ∈ [0;m] be the control

points (n > m is expected). The unknowns are the r

Our interpolation method states that P

is interpolated

by at most three control points C

, C

and C

. We de-

note that by r

= ω

i,1

+ ω

i,2

+ ω

i,3

Let X be the unknown vector (r

)

j∈[0;m]

of radial co-

efﬁcients of the control points C

. Let Y be the vector

)

i∈[0;n]

of radial coefﬁcients of the samples P

. Let

A be the matrix of the weights of interpolation. Each

line of that matrix is the interpolation of one sample,

and holds at most three non-null weights.

The system to solve is AX = Y . Usually, this system

is over-determined since we get as many samples as

we want, while the number of control points remains

limited. It has likely no solution and only an approxi-

mation is needed.

3.2.1 Least-Squares Method

To solve this system, we can use the Least-Squares

Method and set X = (A

−1

Y . This has shown very

good results on smooth functions.

3.2.2 Linear Programming

A common problem of the least-squares method is

that there may be a high local error as long as the er-

ror is low elsewhere. In (Marzais et al., 2006), this

problem is addressed using linear programming. By

minimizing the inﬁnite norm of the error, this method

tries to output results with a locally limited error.

For our problem, that linear programming method

consists in solving Equation 5 to minimize the inﬁ-

nite norm of the error.

−1.h ≤ ((AX −Y )

)

i∈[0;n]

≤ 1.h (5)

h is the error that is to be minimized

However, better results are obtained in our case by

minimizing the inﬁnite norm of the relative error

(Equation 6). This causes small scale areas to be less

perturbed, at the cost of less precise big scale areas.

−1.h ≤



(AX −Y)



i∈[0;n]

≤ 1.h (6)

As a compromise, we obtained best results by divid-

ing with the square root of the value (Equation 7).

−1.h ≤



(AX −Y)

√



i∈[0;n]

≤ 1.h (7)

Indeed, as it can be seen on Figure 7 (c), some areas

are very well approximated, while other are less pre-

cise. If the maximal error is found around the peaks, it

may be a small error compared to the peak scale, but

a big error compared to the small values of the shape.

A FAST INTERPOLATION METHOD TO REPRESENT THE BRDF IN GLOBAL ILLUMINATION

Thus, if the error cannot be less than ε, this may cause

perturbations in the range [−ε;ε]. This would spoil

small scale areas for which ε is not a small value. By

taking the relative error, each area is constrained to be

as good as possible. This is illustrated in Fig. 9, with

a large peak as shape.

(a) (b)

(c)

Figure 9: (a) Linear solving with absolute error may cause

small scale areas to be perturbed. (b) Linear solving with

relative error improves small scale areas but is less precise

on big scale ones. (c) A compromise can be found with

the relative error by dividing by the square root of the value

instead of the value itself.

After many tests, the least-squares method kept

performing a little better than the linear programming

method. Both methods are easy to implement and

may be of interest for complex shapes.

3.3 Deforming Existing Shapes

The set of coefﬁcients characterizing the decompo-

sition of a function, on a basis of functions, cannot

be easily interpreted. Most of the time, the ﬁrst co-

efﬁcients characterize the shape globally, and addi-

tional coefﬁcients introduce local details; but deform-

ing the shape might have an impact on every coef-

ﬁcient. Therefore, it not easy to deform an existing

shape, just by acting on the coefﬁcients, since the con-

sequences are difﬁcult to foresee.

Our interpolation method has the particularity that

any point is characterized by at most three coefﬁcients

that are very easy to determine. Pulling or pushing a

point away from the center of the shape has an effect

only on these three coefﬁcients. To change the radius

of a point of an existing shape, it is only necessary

to recompute the weights of the three associated con-

trol points. Let us consider P(r, θ, φ) interpolated by

, θ

, φ

), C

, θ

, φ

) and C

, θ

, φ

). This is

denoted by r = ω

+ ω

Let P

(r + δr, θ, φ) be the new point P. Then we must

ﬁnd δr

, δr

and δr

such that r +δr = ω

+δr

+ δr

) + ω

+ δr

A trivial soluion is δr = δr

= δr

, since

+ δr) + ω

+ δr) =

+ ω

| {z }

+δr (ω

+ ω

)

| {z }

However, it is a bad solution since it is just a shift

of the spherical triangle in which P is falling. The risk

is to perturbate other interpolated point too much. A

better approach is to weighten δr

by ω

, so that a con-

trol point is shifted according to its importance in the

interpolation of P.

For instance, if we require δr

to be proportional to

, we just have to divide by

∑

to normalise.

Hence, the solution we chose is :

δr

∑

δr (8)

3.4 Rotation

To perform an efﬁcient interpolation, our method does

not allow the angles of the control points to change.

Therefore, the rotation cannot be applied to the con-

trol points. It is possible, but too expensive, to recom-

pute the control points by resampling the function,

rotating the samples, and reapplying Least-Squares

Method (or Linear Programming) to get the new con-

trol points. The rotation being a critical function, it

should be more efﬁcient than that.

3.4.1 Permutation Approach

In our control points system, a rotation can be ap-

proximated by a permutation of the control points,

by assigning to each virtually rotated control point,

one (another) of the (non-rotated) control points, most

likely the closest (see Figure 10).

Such a process is very fast since the rotation is then

reduced to a set of pre-computed permutations for rel-

evant angles. The drawback is that the rotation is no

more a continous process, can be transformed into the

Identity for small angles, and that much error can be

accumulated in a sequence of rotations.

To compute the permutation associated to a rota-

tion, a naive method would be to match each virtually

rotated control point to the closest control point, start-

ing from the best matching (with minimal error) and

ending with the worst one. The problem is that it can

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

end with catastrophic matchings since less and less

control points remain free while the matchings occur

(see Figure 11).

To overcome the problem, another strategy can be

adopted: ﬁrst, the best matching is realized with a

control point C. Then each matching is done the best

possible, starting from the point which is the closest

to C and ending with the furthest one. That prevents a

point to become isolated, with all its neighbours hav-

ing realized a match (monopolizing the control points

around). This would be the cause of a poor matching.

Figure 10: Matching each

virtually rotated control

point (dotted stroke) to the

closest non-rotated point

(plain stroke).

Figure 11: “Best-matchings

ﬁrst” may end in catas-

trophic matchings if not

enough control points re-

main free. Here, the central

point is poorly matched.

3.4.2 A Continuous Approach

The best representation of the rotated shape would be

found by resampling it, and perform LSM again to

solve the constrained system. It is not affordable, but

makes it obvious that the weights of the control points

should be reconsidered rather than merely permuted.

As a matter of fact, it is rather easy to perform, by in-

terpolating the virtually rotated control points on the

original, non-rotated, control points.

Each control point, when rotated, can be seen as a

sample, that is to be interpolated by three “real” con-

trol points. Thus, a “real” control point can be in-

volved in the interpolation of many “virtually rotated”

control points. It is given one weight per interpola-

tion. Then, its new radial distance is set according to

a weighted sum of the interpolations for which it is

participating. Its new position is a compromise and

does not necessarly satisfy each interpolation, but this

simpliﬁed processus gives us a simple, continuous ro-

tation method.

3.5 Direction-Driven Global

Illumination Solver

Global illumination algorithms usually use patches as

scene elements, and gathers for each patch the quan-

tity of light received by other patches visible from

there. By iterating this algorithm, light propagates in

the scene and converges towards a radiosity solution.

Another approach presented in (Chatelier and Malgo-

uyres, 2006) uses a special method to compute visi-

bility between volumetric scene elements, and the ra-

diosity algorithm is then parametrized by a set of di-

rections in space to consider. Light is transported only

on these directions. This comes from the fact that vis-

ibility computations are factorized along some rays

(Figure 12).

A consequence of this direction-driven radiosity

solver is that it is also possible to factorize computa-

tions that are done along a ray. Indeed, the interpola-

tion method described in the present paper computes

weights for a given direction (θ, φ). Combined with

the direction-driven solver, this computation can be

factorized for all the scene elements that lie along a

ray. It results in an additional optimization that our

method brings to global illumination solving.

This is not a marginal optimization. We have also

used our BRDF representation in the radiative trans-

fer problem (Lenoble, 1993); in this problem, a cloud

is illuminated and the energy propagations occur ac-

cording to some distributions that are called phase

functions. These phase functions can be represented

by 2D spherical functions. Only one global coordi-

nate system is used, since the volumic elements that

are representing the cloud are not oriented. So, no

rotation is needed. In this context, if N voxels are en-

coding the cloud, each one is queried for its radiance

distribution in the current direction (θ, φ). Then, the

computation of the weights for (θ, φ) can be factor-

ized for the N voxels.

Figure 12: A direction-driven algorithm can factorize the

weights computation of all elements lying along a ray, when

querying values from radiance distributions.

4 EXPERIMENTAL RESULTS

To compare our implementation of BRDFs using

control points, with an implementation using Spher-

ical Harmonics, we have used our radiosity solver

(Chatelier and Malgouyres, 2006). The spherical

harmonics relies on the SpharmonicKit (Kostele and

Rockmore, 2004), which performs very well, so that

the performance gap should not be a defect of our

implementation of the spherical harmonics.

Figure 13 shows that our method largely outperforms

the spherical harmonics approach. Moreover, we

did not implement the rotation of the spherical

A FAST INTERPOLATION METHOD TO REPRESENT THE BRDF IN GLOBAL ILLUMINATION

harmonics, so that it is not even slowed down by

their known bottleneck. The scene that has been used

is a very simple assemblage of cubes, with diffuse

BRDFs. It has been discretized into 13000 voxels for

the solver.

45 111 223 489 1131 2013

195

451

808

171

Control Points (162 coeffs) Spherical Harmonics (64 coeffs)

13000 voxels, 5 itérations

number of directions

seconds

Figure 13: The performance of the control points method

(plain stroke) is far better than the spherical harmonics.

(a) (b)

Figure 14: (a) Simple scene. (b) Raw data per voxel after

radiosity solving.

REFERENCES

Ashikhmin, M. and Shirley, P. (2000). An anisotropic

Phong BRDF model. Journal of Graphics Tools: JGT,

5(2):25–32.

Blanco, M. A., Florez, M., and Bermejo, M. (1997). Evalu-

ation of the rotation matrices in the basis of real spher-

ical harmonics. J. Molecular Structure (Theochem),

419:19–27.

Chatelier, P. Y. and Malgouyres, R. (2006). A low-

complexity discrete radiosity method. Computers &

Graphics, 30:37–45.

Erdelyi, A. (1953). Higher transcendental functions, vol-

ume 2. McGrawHill book company, Inc.

Franc¸ois X. Sillion and Claude Puech (1994). Radiosity &

Global Illumination. Morgan Kaufmann Publishers,

Inc.

Kautz, J., Sloan, P.-P., and Snyder, J. (2002). Fast, arbi-

trary brdf shading for low-frequency lighting using

spherical harmonics. In EGRW ’02: Proceedings of

the 13th Eurographics workshop on Rendering, pages

291–296.

Koenderink, J. J., van Doorn, A. J., and Stavridi, M.

(1996). Bidirectional reﬂection distribution function

expressed in terms of surface scattering modes. In

ECCV ’96: Proceedings of the 4th European Con-

ference on Computer Vision-Volume II, pages 28–39,

London, UK. Springer-Verlag.

Kostele, P. and Rockmore, D. (2004). The

SpharmonicKit and S2Kit libraries.

http://www.cs.dartmouth.edu/ geelong/sphere.

riv

anek, J., Konttinen, J., Bouatouch, K., Pattanaik, S.,

and

ara, J. (2005). Fast approximation to spherical

harmonic rotation. In SCCG ’06: Proceedings of the

22nd spring conference on Computer graphics (to ap-

pear), New York, NY, USA. ACM Press.

Lenoble, J. (1993). Atmospheric Radiative Transfer. A.

Deepak Publishing.

Marzais, T., Grard, Y., and Malgouyres, R. (2006).

l p−ﬁtting approach for reconstructing parametric sur-

faces from point clouds. In International Confer-

ence on Computer Graphics Theory and Applications,

Set

ubal, Portugal, pages 325–330.

Neumann, A. (2001). Constructions of Bidirectional Re-

ﬂection Distribution Functions. PhD thesis, Institute

of Computer Graphics and Algorithms, Vienna Uni-

versity of Technology, Favoritenstrasse 9-11/186, A-

1040 Vienna, Austria.

Ohrstr

om, M. Spherical harmonics, precomputed radiance

transfer and realtime radiosity in computer games.

http://citeseer.ist.psu.edu/685526.html.

Rusinkiewicz, S. (1997). A survey of brdf

representation for computer graphics.

http://www.cs.princeton.edu/˜smr/cs348c-

97/surveypaper.html.

Rusinkiewicz, S. (1998). A new change of variables for efﬁ-

cient BRDF representation. In Drettakis, G. and Max,

N., editors, Rendering Techniques ’98 (Proceedings of

Eurographics Rendering Workshop ’98), pages 11–22,

New York, NY. Springer Wien.

Schr

oder, P. and Sweldens, W. (1995). Spherical wavelets:

efﬁciently representing functions on the sphere. Com-

puter Graphics, 29(Annual Conference Series):161–

172.

Sillion, F. X., Arvo, J. R., Westin, S. H., and Greenberg,

D. P. (1991). A global illumination solution for gen-

eral reﬂectance distributions. In SIGGRAPH ’91: Pro-

ceedings of the 18th annual conference on Computer

graphics and interactive techniques, pages 187–196,

New York, NY, USA. ACM Press.

Ward, G. J. (1992). Measuring and modeling anisotropic re-

ﬂection. In SIGGRAPH ’92: Proceedings of the 19th

annual conference on Computer graphics and interac-

tive techniques, pages 265–272, New York, NY, USA.

ACM Press.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications