SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE

SIMPLIFICATION

Sumanta Guha, Paul Janecek and Nguyen Duc Cong Song

CSIM Program, Asian Institute of Technology, P.O. Box 4, Klong Luang, Pathumthani 12120, Thailand

Keywords:

Curvature, curve simpliﬁcation, Douglas-Peucker, level of detail, polygonal curve, polyline, simpliﬁcation

algorithm, SimpliPoly.

Abstract:

A curvature-based algorithm to simplify a polygonal curve is described, together with its implementation. The

so-called SimpliPoly algorithm uses B´ezier curves to approximate pieces of the input curve, and assign curva-

ture estimates to vertices of the input polyline from curvature values computed for the B´ezier approximations.

The implementation of SimpliPoly is interactive and available freely on-line. Empirical comparisons indicate

that SimpliPoly performs as well as the widely-used Douglas-Peucker algorithm in most situations, and sig-

niﬁcantly better, because it is curvature-driven, in applications where it is necessary to preserve local features

of the curve.

1 INTRODUCTION

LOD (Level of Detail) management is becoming an

increasingly important issue in interactive computer

graphics and visualization because of performance

requirements in rendering and transferring complex

images. Objects are often stored in multiple LODs,

or resolutions, and the appropriate LOD chosen for

a subsequent application. A variety of techniques

have been developed for the purpose of computing

LODs, typically beginning with the original object,

and then increasingly coarse, a process called simpli-

ﬁcation. See (Heckbert and Garland, 1995; Luebke

et al., 2003) for surveys. Most of the current litera-

ture in computergraphics and available softwaredeals

with the simpliﬁcation of surfaces in 3D.

We focus in this paper on a somewhat restricted

LOD problem, that of simplifying a plane polygonal

curve, also called polyline. Nevertheless, this prob-

lem is of interest in several application areas as well,

ranging from sketch simpliﬁcation to map simpliﬁca-

tion in GIS (Geographical Information Systems). Fig-

ure 1 gives an example of the utility of polyline sim-

pliﬁcation: the ﬁgure on the right is about a sixth as

complex as the original one the left, yet is likely faith-

ful enough to be adequate for many purposes, while

the one in the middle at much less than half the com-

plexity is almost indistinguishable from the original.

The main contribution of this paper is an algo-

rithm and its derivative software package – together

called SimpliPoly – that can be used to interactively

simplify a polyline. SimpliPoly makes a novel ap-

plication of the notion of curvature from differential

geometry to the simpliﬁcation problem. In particular,

our approach is to estimate the curvature of a polyline

at its vertices.

A polylineC, except for the trivial situation where

all its vertices lie on a straight line, is not smooth.

Accordingly, differential geometric measures of cur-

vature cannot be applied directly to C itself. Our

method is, instead, to ﬁrst approximate pieces of C

with B´ezier curves, and then “lift” curvature values

from points of the approximations to vertices of C.

Subsequently, vertices ofC with low curvature are re-

moved on the premise that they lie on “straightish”

parts of C.

The technique is motivated mostly by heuristic ar-

guments, our goal ﬁrst and foremost being simple and

practical software. We do not prove results about the

quality of the simpliﬁcation. Unfortunately, it seems

difﬁcult to do so, giventhe nature of the heuristics em-

ployed; nevertheless, they are all fairly intuitive and

166

Guha S., Janecek P. and Duc Cong Song N. (2007).

SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 166-171

DOI: 10.5220/0002072801660171

 SciTePress

(a) (b) (c)

Figure 1: Multiple LODs: (a) 150 vertices (b) 60 vertices (c) 26 vertices.

justiﬁed by the context. Moreover, the SimpliPoly

software package is designed to be used interactively,

so that the user monitors the output until she per-

ceives the simpliﬁcation to be satisfactory, rather than

depending upon an a priori guarantee of its quality.

Our results – which the reader is invited to verify

using the on-line Java version (SimpliPoly, 2006) –

indicate that SimpliPoly indeed works well in prac-

tice, producing faithful simpliﬁcations over a range of

user-controlled quality parameters. Its interface too is

easy-to-use making SimpliPoly an attractive option in

various application domains.

Currently, the polyline simpliﬁcation algorithm

used most commonly in practice is the Douglas-

Peucker algorithm (Douglas and Peucker, 1973),

which is a recursive algorithm based on reducing a

distance error between an input polyline and its sim-

pliﬁcation. Douglas-Peucker is easily implemented,

fairly efﬁcient, and generally produces good-quality

output – all reasons for its popularity. However,

Douglas-Peucker is purely “distance-error driven”; it

does not “recognize” local features, e.g., a sharp turn,

a protrusion, etc., and, therefore, makes no attempt to

preserve such features as it simpliﬁes. SimpliPoly, on

the other hand, being “curvature-driven”, does recog-

nize features and tends to keep them. At the same

time, because stretches of a polyline with low dis-

tance error from a simpliﬁcation tend in practice to

be of low curvature values as well, the ability of Sim-

pliPoly to simplify such stretches appears to be com-

petitive with Douglas-Peucker.

At present, the theoretically best algorithms for

polyline curve simpliﬁcation are from Agarwal et al.

(Agarwal et al., 2002), who obtain provably near-

optimal simpliﬁcations within speciﬁed distance er-

ror bounds. However, their algorithms are complex

and there seems to be no practical implementation yet.

Moreover, the only curvature-based simpliﬁcation al-

gorithms that we are aware of are due to Kim et al.

(Kim et al., 2002) and references therein, all of which

deal with surfaces rather than curves. Again, these

algorithms are all fairly complex and no code seems

available.

The next four sections discuss successively the

SimpliPoly algorithm in detail, its analysis, applica-

tions, and, ﬁnally, conclusions.

2 ALGORITHM

Let C be a polyline joining the n + 1 vertices

,...,v

, where n ≥ 5. SimpliPoly computes the

B´ezier approximationof a “sliding window”of length

ﬁve vertices of C as follows. First, it determines the

B´ezier curve c

(u),0 ≤ u ≤ 1, of order ﬁve with ver-

tices v

,...,v

as control points, then the curve

(u) with v

,...,v

, as control points, and so on,

till the curve c

n−4

(u) with v

n−4

n−3

,...,v

as control

points.

The formula for c

(u) is

(u) =

i+4

∑

r=i

r,4

(u)v

i+r

, 0 ≤ i ≤ n− 4

where

r,4

(u) =





(1− u)

4−r

, 0 ≤ r ≤ 4

are the blending functions, which happen to be the

Bernstein polynomialsof degree four in this case. See

Farin (Farin, 2001) for a discussion of B´ezier theory

in general.

Note that there is no particular reason to choose

order ﬁve for the B´ezier approximation, other than

it seems to span a reasonable number of vertices of

C, and yet is not large enough to be computationally

problematic.

Figure 2 shows the ﬁrst two approximating curves

for a polyline: c

(u) (solid) and c

(u) (dashed).

Next, for each B´ezier curve c

(u), 0 ≤ i ≤ n − 4,

SimpliPoly determines the curvature at the three inte-

rior points c

(0.25), c

(0.5) and c

(0.75), and “lifts”

them to the control vertices v

i+1

, v

i+2

and v

i+3

, re-

spectively. This is done as the blending function cor-

responding to each of these three vertices has max-

imum value at the point of c

(u) whose curvature is

SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION

167

c (0.25)

c (0.5)

c (0.75)

Figure 2: The solid curve is c

(u), the dashed one c

(u), and the arrows point in the direction curvature is lifted (only the

liftings from c

(u) are shown).

v vv v

v v

0.2

0.3

0.33

0.5

c (u)

Figure 3: Schematic illustration: determining the pseudo-curvature of a polyline vertex from a sliding window of B´ezier

approximations.

lifted. Intuitively, each control vertex picks up its

curvature from the point of the curve at which it has

the most inﬂuence. Curvature at the end vertices are

not used on the premise that data from a surround-

ing neighborhood of a point should be available if the

curvature is to be applied for the purpose of simpli-

ﬁcation (even though it can be mathematically calcu-

lated).

Figure 2 illustrates the scheme (only the curvature

liftings from the ﬁrst B´ezier curve are indicated). The

formula used to compute curvature is from classical

differential geometry (Do Carmo, 1976): the curva-

ture of a plane curve c(t) = x(t)i+ y(t)j is given by

κ(t) =

′

(t)y

′′

(t) − x

′′

(t)y

′

(t)

′

(t)

+ y

′

(t)

)

3/2

As the 5-vertex window slides from one end of C

to the other, all the vertices from v

to v

n−3

lift cur-

vature values from three different B´ezier curves c

(u)

each, while v

and v

lift no curvature values, v

and

n−1

lift one each, and v

and v

n−2

two each. Figure 3

is a schematic illustration. Heuristically, next, Sim-

pliPoly averages the set of curvature values at each

vertex v

(except for v

and v

, of course) to deter-

mine the so-called pseudo-curvature k

, 1 ≤ i ≤ n− 1,

of that vertex, a value used as a curvature estimate.

E.g., if the curvatures values of c

(u),c

(u) are

as indicated in Figure 3 (at parameter values 0.75, 0.5

and 0.25, respectively), then the pseudo-curvature of

is 0.33.

Finally, SimpliPoly removes all vertices v

whose

pseudo-curvature k

≤ κ, where κ is a user-deﬁned

curvature threshold.

An option in SimpliPoly allows the user to con-

trol in a simple manner the distance error in the sim-

pliﬁcation as vertices are removed. SimpliPoly re-

moves vertices by processing from the high end to the

low, beginning possibly with v

n−1

. If an error thresh-

old ε > 0 is speciﬁed, then, before removing a vertex

according to the pseudo-curvature constraint, Sim-

pliPoly determines the perpendicular distance d of v

to the straight line joining v

i−1

and v

i+1

, and, if this

distance exceeds ε, v

is skipped, i.e., not removed.

See Figure 4.

SimpliPoly can be run on-line, or, locally, by

downloading the source – the URL is cited (Sim-

pliPoly, 2006). A Java run-time is required.

3 ANALYSIS

The run-time of SimpliPoly is asymptotically linear

in the number n of vertices of the polyline being sim-

pliﬁed. This is trivial to see: there are O(n) window

positions, with a constant amount of curvature com-

putation for the B´ezier curve in each; subsequently,

there is a constant amount of computation per vertex

of the polyline to determine the pseudo-curvature at

that vertex, and process it for possible removal.

Comparison with Douglas-Peucker: For polygonal

curve simpliﬁcation, Douglas-Peucker (Douglas and

Peucker, 1973) is the algorithm “to beat”. We have

experimented with Douglas-Peucker and SimpliPoly

extensively. From a subjective evaluation of the two

– we compared, therefore, the perceived quality of

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

168

i−1

i+1

Figure 4: v

is not removed if d > ε.

their outputs – SimpliPoly almost always matches

Douglas-Peucker, and is clearly superior in certain

cases for reasons which are not hard to understand,

and which we’ll discuss momentarily.

Theoretically, the worst-case complexity of a

straightforwardrecursive implementationof Douglas-

Peucker is O(mn), where n is the input number of ver-

tices and m the output number. The Douglas-Peucker

worst-case complexity can be improved to O(nlogn)

by using convex hulls to speed up distance compu-

tations (Hershberger and Snoeyink, 1992). As dis-

cussed earlier, SimpliPoly is always O(n), regardless

of output size. However, from our experiments with

up to a few thousand vertices (which bounds the com-

plexity of most practical applications) on a reasonable

desktop, time consumed seems not to be an issue with

either algorithm.

Qualitatively, the major difference between the

two is best seen in a canonical example, as in Fig-

ure 5. The original polyline, which is not drawn, has

the 20 vertices shown. Both SimpliPoly and Douglas-

Peucker were applied to achieve a 60% reduction to

8 vertices, the former by increasing the curvature

threshold, the latter by increasing the distance error

allowed. The SimpliPoly output is the solid line, the

Douglas-Peucker output the dashed one.

As can be seen, SimpliPoly respects the corners

(features) “more” than Douglas-Peucker. The rea-

son, of course, is that the former examines pseudo-

curvatures through a local window, thereby detecting

features that the global Douglas-Peucker method can-

not. On the two straightish (though still mildly noisy)

stretches on either side of the hump both algorithms

perform equally.

4 APPLICATIONS

Curve simpliﬁcation algorithms are used to reduce

the complexity of 2D graphical scenes in a variety

of application domains. As described in the intro-

duction, curve simpliﬁcation is often used to pre-

calculate a family of models at successively coarser

levels of detail. This allows an application to dy-

namically make trade-offs between image quality and

performance by choosing between representations of

varying complexity. For example, a drawing program

might use simpliﬁed models while the user is interac-

tively scrolling or zooming a scene in order to main-

tain high frame rates.

The main strength of the SimpliPoly algorithm,

when compared with a global error-based algorithm

such as Douglas-Peucker,is its sensitivity to local cur-

vature. This makes it particularly promising for appli-

cations where distinctive local features must be pre-

served. For example, terrain features in cartographic

maps, such as coastlines and elevation lines, are often

”noisy”, with many sharp local changes in direction

that vary in magnitude over the length of the feature.

An error-based algorithm will focus on the vertices

that extend outside a particular tolerance. In contrast,

a curvature-based algorithm will focus on the corners

(the points of high curvature) that deﬁne the distinc-

tive shape of the feature. SimpliPoly also includes an

error threshold that can be used interactively to cap-

ture features that change more gradually (regions of

low curvature).

It is difﬁcult for any single algorithm to create a

high-quality simpliﬁcation for both sharp and grad-

ual changes in curvature. The SimpliPoly software

allows the user to interactively adjust the curvature

and error thresholds of the algorithm to obtain a sim-

pliﬁcation of the appropriate complexity and qual-

ity. Figure 6 shows a comparison of how the Sim-

pliPoly and Douglas-Peucker algorithms simplify a

curve with both sharp and gradual changes of curva-

ture. In the top example, both algorithms have re-

duced a curve with 58 vertices to 7, a reduction of

87%. The SimpliPoly algorithm is more effective at

capturing the corners of the sharp features, while the

DP algorithm is slightly more effective with the grad-

ual curves. The middle example shows the result of

increasing the number of vertices to 10 (a reduction

of 82%). Both algorithms have improved slightly by

capturing more detail of the sharp and smooth fea-

tures. The bottom example shows the effect of reduc-

ing the error threshold and increasing the curvature

threshold for the SimpliPoly algorithm, which results

SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION

169

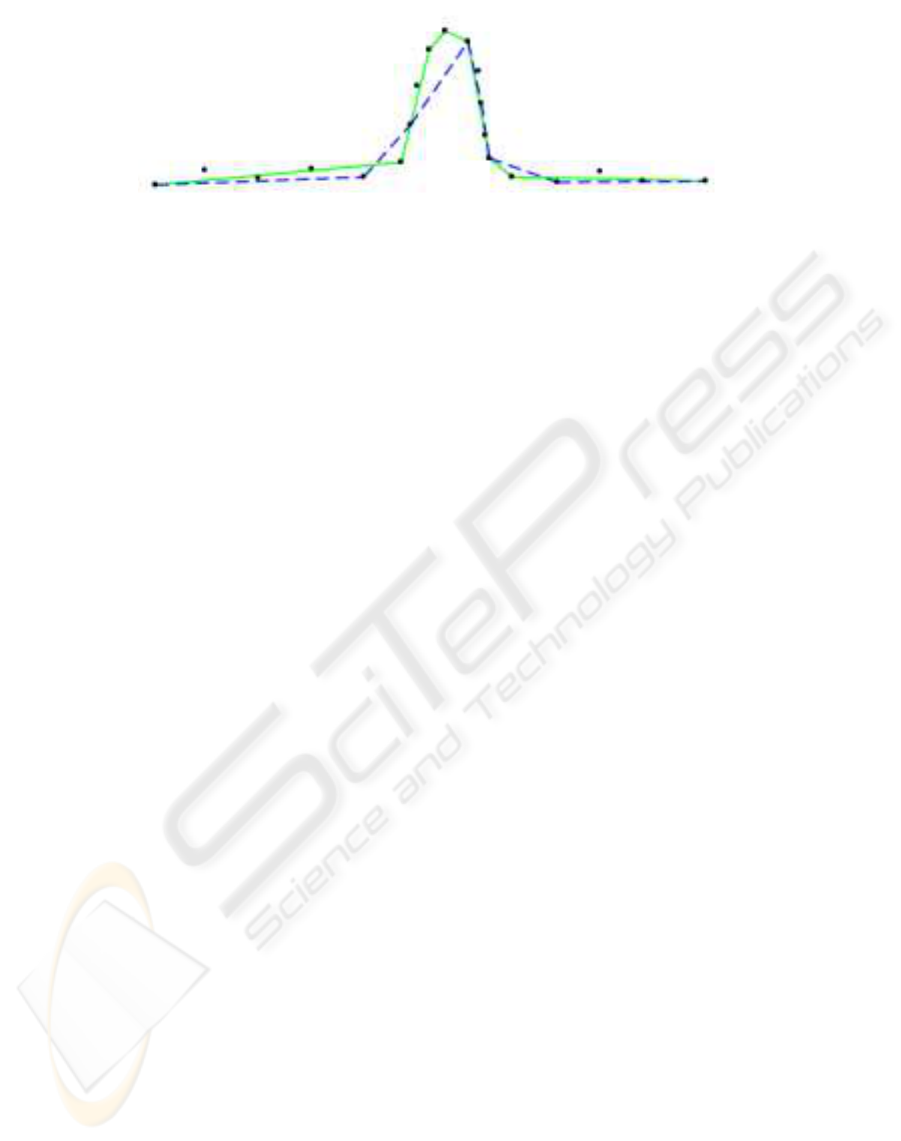
Figure 5: SimpliPoly (solid line) vs. Douglas-Peucker (dashed line): the original polyline (not shown) has 20 vertices (shown),

while both simpliﬁcations have 8 vertices each, a reduction of 60%.

in a simpliﬁcation of equal complexity (10 vertices)

but noticeably better quality.

5 CONCLUSIONS

The primary contribution of this paper is the descrip-

tion of a novel and high-quality curve simpliﬁca-

tion algorithm with a working implementation that is

available for practical use.

The SimpliPoly algorithm is a linear-time 2D

curve simpliﬁcation method based on curvature es-

timation via piecewise B´ezier approximations. The

software implementation (available on-line at (Sim-

pliPoly, 2006)) allows the user to interactively adjust

the curvature and error thresholds to control trade-offs

between quality and complexity. The algorithm gives

results of comparable – and often superior – quality

to the popular Douglas-Peucker algorithm.

Future work remains to be done, in particular the

following:

1. Empirical evaluation of the algorithm over large

data sets, e.g., Agarwal et al. (Agarwal et al.,

2002) use polygonal curves obtained from the

Protein Data Bank (Protein Data Bank, 2006).

2. Allowing ﬁner control of feature-sensitivity: pos-

sibilities include allowing change in the sliding

window size from its current ﬁxed ﬁve, using

curve types other than B´ezier, etc.

3. Hybridizing with a Douglas-Peucker type algo-

rithm, that is more effective in smoothing gradual

(global) changes, to obtain the “ultimate” polygo-

nal curve simpliﬁcation method.

REFERENCES

Agarwal, P. K., Har-Peled, S., Mustafa, N., and Wang, Y.

(2002). Near-linear time approximation algorithms

for curve simpliﬁcation. In Tenth European Sympo-

sium on Algorithms, pages 29–41.

Do Carmo, M. P. (1976). Differential Geometry of Curves

and Surfaces. Prentice Hall.

Douglas, D. H. and Peucker, T. K. (1973). Algorithms for

the reduction of the number of points required to rep-

resent a digitized line or its caricature. The Canadian

Cartographer, 10:29–41.

Farin, G. (2001). Curves and Surfaces for CAGD: A Prac-

tical Guide, volume 5. Morgan Kaufmann.

Heckbert, P. S. and Garland, M. (1995). Survey of polyg-

onal surface simpliﬁcation algorithms. Technical Re-

port CMU-CS-95-194, Carnegie Mellon University.

Hershberger, J. and Snoeyink, J. (1992). Speeding up

the Douglas-Peucker line simpliﬁcation algorithm. In

Fifth International Symposium on Spatial Data Han-

dling, pages 134–143.

Kim, S.-J., Kim, C.-H., and Levin, D. (2002). Surface sim-

pliﬁcation using a discrete curvature norm. Computers

& Graphics, 26:657–663.

Luebke, D., Reddy, M., Cohen, J. D., Varshney, A., Watson,

B., and Huebner, R. (2003). Level of Detail for 3D

Graphics. Morgan Kaufmann.

Protein Data Bank (2006). http://www.rcsb.org/pdb/.

SimpliPoly (2006). Polygonal

curve simpliﬁcation software:

http://www.cs.ait.ac.th/˜ guha/SimpliPoly/simpliPoly.html.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

170

Figure 6: SimpliPoly (solid line) vs. Douglas-Peucker (dashed line) for different curvatures at the same complexity. The

original curve of 58 vertices is reduced to 7 vertices in the top ﬁgure and 10 in the bottom two ﬁgures. The bottom ﬁgure

shows the improvement found with interactively adjusting the error and curvature thresholds of the SimpliPoly algorithm.

SIMPLIPOLY: CURVATURE-BASED POLYGONAL CURVE SIMPLIFICATION

171