
PLAUSIBLE MOTION SIMULATION: INCHWORM VS. ROLLER
Juha Holopainen
Department of Computer Science, University of Kuopio
PO Box 1627, 70211 Kuopio, Finland
Mauno R
¨
onkk
¨
o
Department of Computer Science, University of Kuopio
PO Box 1627, 70211 Kuopio, Finland
Keywords:
Particle systems, plausible motion simulation, intelligent control, emergent dynamics.
Abstract:
In this paper, we study the use of a specific particle system in motion simulation. The novelty of the particle
system is that, with it, everything is formalized in a systematic and uniform manner using just six matrices.
We illustrate use of the particle system by presenting a challenging environment where two different entities,
Inchworm and Roller, are tested and their behavior is examined. As the main contribution, we demonstrate
here that, despite its simplicity, the particle system supports plausible motion simulation for organic and mech-
anistic motion. In addition, as the entities are modeled in a systematic and uniform manner, they are reusable.
1 INTRODUCTION
Objects and substances displaying emergent dynam-
ics are often simulated with particle systems (Eber-
hardt et al., 1996; Wejchert and Haumann, 1991;
Witkin, 1997; Wojtan et al., 2006).
Here, we present a particle system (R
¨
onkk
¨
o,
2006b) which captures a wide range of dynamics
without being too complex. This is achieved by for-
malizing the components in a systematic and uniform
manner using matrices, as discussed in Section 2.
Due to the formalization, the particle system is
modular, and the components can be reused in dif-
ferent settings. Furthermore, because the interaction
of the components arises as emergent dynamics, the
components automatically adapt to the new settings.
As the main contribution, we demonstrate here
with two active entities that the particle system sup-
ports plausible motion simulation for both organic
and mechanistic motion.
The two entities are Inchworm and Roller, which
are introduced in Sections 3 and 4 respectively. Inch-
worm is an organic entity displaying life-like motion.
Roller, in turn, is a mechanical entity, displaying clas-
sical mechanics. The entities were tested on different
terrains. The terrain which revealed the most interest-
ing dynamics, along with the test runs, is presented in
Section 5. The implications and the plan for further
development are then discussed in Section 6.
2 THE PARTICLE SYSTEM
In the particle system (R
¨
onkk
¨
o, 2006b), there is a
fixed and finite number of particles. They are unit
balls with uniformly distributed, constant unit mass.
The particles are modeled using six matrices. The
matrices p, v, d, and m capture the position, velocity,
damping coefficient, and memory, respectively. The
matrices b and c indicate which particles are bound
to each other or collide with each other. The particles
are identified by the rows of the matrices. The values
of p
i
, v
i
, and m
i
are three-dimensional vectors, and
d
i
is a real valued number. Lastly, b and c are square
matrices, where any b
ij
and c
ij
is either 0 or 1.
The dynamics of all the particles are governed by
a model of motion. It is a numerical approximation
of the trivial model of motion with forward error cor-
rection. Let t denote a fixed time step, B denote a
bond function, C denote a collision function, R de-
note a model specific reaction function, and M denote
a model specific memory update function. Then, the
motion of a particle i is computed:
p
0
i
= p
i
+ tv
0
i
v
0
i
= d
i
v
i
+ B
i
(p) + C
i
(p) + R
i
(p, v, m)
m
0
i
= M
i
(p, m)
Here, the updated position, p
0
i
, is computed using
the updated velocity, v
0
i
, which is computed using af-
71
Holopainen J. and Rönkkö M. (2007).
PLAUSIBLE MOTION SIMULATION: INCHWORM VS. ROLLER.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 71-74
DOI: 10.5220/0002073500710074
Copyright
c
SciTePress

fecting forces. The binding forces are computed with
respect to the initial positions, denoted by p
0
, as:
B
i
(p) =
X
j
b
ij
(p
j
− p
i
)(1 −
kp
0
j
− p
0
i
k
2
kp
j
− p
i
k
2
)
Similarly, the collision forces are computed as:
C
i
(p) =
X
j
c
ij
(p
j
− p
i
) min{0, 1 −
4
kp
j
− p
i
k
2
}
In short, the binding forces try to maintain the initial
distance between the particles designated by b. The
collision forces push apart any overlapping particles
that are allowed to collide by c. Two particles overlap,
when their distance is less than the sum of their radii.
When modeling, we first assign particles to the
components. We then define the initial values for p,
m, d, b, and c. The matrix v is zero initially. Lastly,
we define the functions R and M . The simulation is
then an iterative computation of the model of motion.
In the following, we assume t = 0.01 as the time
step. Also, we use a conditional expression hP i,
which returns 1 if the predicate P holds and 0 oth-
erwise.
3 INCHWORM
Inchworm, presented originally in (R
¨
onkk
¨
o, 2006b),
is similar to Arctic Caterpillar (Miller, 1988). It has
a body and two leg particles. The body is composed
of 60 particles, forming a muscle that operates in two
phases: it contracts and relaxes, as captured in Figure
1. When contracting Inchworm grasps on to the road
with its front leg, and when relaxing, it grasps on to
the road with its tail leg. Contraction and relaxation
are repeated sequentially, lasting the same number of
iteration rounds. For this purpose, Inchworm uses a
memory. In the sequel, we identify a particle i with:
b ody(i) = h0 ≤ i < 60i
legs(i) = h60 ≤ i < 62i
road(i) = h62 ≤ ii
Consider a body particle i of Inchworm, that is
body(i) = 1, and any particle j. Then, the model of
the body is:
p
0
i
= (15, 4, −0.3i + 5)
m
0
i
= (0, 0, 0)
d
i
= 0.95
b
ij
= (1 − road(j)) · h0 < kp
0
j
− p
0
i
k < 2.5i
c
ij
= road(j) + (1 − road(j))h2.5 < kp
0
j
− p
0
i
ki
R
i
(p, v, m) = 0.1h0 < m
(i,1)
ih15 ≤ i < 45i · (p
53
− p
61
)
M
i
(p, m) = (m
(i,1)
+ 1, 0, 0) − (2000h999 < m
(i,1)
i, 0, 0)
Consider a leg particle i and any particle j. Also, let
α be the nearest road particle, so that the condition
road(α) ∧min
2000
k=62
{kp
k
−p
i
k} = kp
α
−p
i
k holds.
Let β indicate when the leg particle i is supposed to
Figure 1: Inchworm edging its way; the state after the first
contraction on the left, and the state after the first relaxation
on the right.
Figure 2: Roller from the side and from the top. In the
left image, the left side beam misses the road. In the right
image, the right side beam misses the road.
move, that is, β = hi = 60ihm
(0,1)
< 0i+ hi = 61ih0 ≤
m
(0,1)
i Lastly, let γ be the value 1 − β. Then, the
model of the legs is:
p
0
i
= (15.3, 3.8, −15.3(i − 60) + 4.1)
m
0
i
= p
0
i
d
i
= 0.95
b
ij
= body(j) · h0 < kp
0
j
− p
0
i
k < 2.5i
c
ij
= road(j)
R
i
(p, v, m) = 0.5(p
α
− p
i
)
+ 0.2βhi = 60i(p
i
− p
61
) + γ(m
i
− p
i
)
M
i
(p, m) = γm
i
+ βp
i
4 ROLLER
Roller is a system composed of an axle and two
wheels. A simpler version of Roller was presented
earlier in (Holopainen and R
¨
onkk
¨
o, 2006).
The control technique comprises of an observa-
tion technique and a steering technique. The observa-
tion technique uses four beams, as shown in Figure 2,
to detect if there are road particles ahead. Two front
beams observe the ground directly at the front of the
wheels. Two side beams observe the ground slightly
outwards from the front beams.
Based on the observations, the steering technique
steers Roller by rotating one or both of the wheels.
When both of the wheels rotate to the same direction,
Roller moves to that direction. If only one wheel ro-
tates, Roller turns. Roller never rotates wheels to op-
posite directions, as it results in less controllable mo-
tion.
Roller has five steering decisions, shown in Table
1. The decision is based on the beam status. In the
table, the numbers show if the wheels are rotated for-
wards (1), backwards (-1), or freely (0).
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
72

Table 1: Decision table for goal directions.
Beams missing the road Goal direction
none ω
l
= 1 ω
r
= 1
only left side beam ω
l
= 0 ω
r
= −1
only right side beam ω
l
= −1 ω
r
= 0
both left and right side beams ω
l
= −1 ω
r
= −1
left or right front beam ω
l
= −1 ω
r
= −1
For identifying the component of Roller’s particle
i, we use the functions:
wheel(i) = h0 ≤ i < 40i
axle(i) = h40 ≤ i < 79i
road(i) = h79 ≤ ii
As Roller does not use memory, the model for an
axle particle i, with respect to any other particle j, is:
p
0
i
= ((i − 40)/3 − 7, 6, 1.5)
d
i
= 0.999
b
ij
= (1 − road(j))hi 6= ji
c
ij
= road(j)
R
i
(p, v, m) = (0, −0.32, 0)
Consider a wheel particle i and any particle j.
Also, for i, let α = i div 20, β = j div 20, and
γ = i mod 20. Then, the model is:
p
0
i
= 2.1(5α, cos(0.2πγ), sin(0.2πγ)) + (−6, 6, 1.5)
d
i
= 0.999
b
ij
= wheel(j)hα = βihi 6= ji + axle(j)
c
ij
= road(j)
As mentioned earlier, the observation technique
uses four beams. Formally, all the beams are identi-
fied by an origin, ~o, and a directional vector, ~r. Let
norm(v) denote the normalized vector of v, that is
norm(v) =
v
kv k
. Let ~a be an axle vector, that is,
~a = p
78
− p
40
, and let ~y be ~y = (0, 20, 0). Then,
the axle’s normal is ~n = norm(~a × ~y), and a planar
normal is ˜n = (3~n
1
, ~n
2
, 3 ~n
3
). Now, the four beams
are defined using cross products:
left front beam: ~o = p
40
~r = (9~n
1
, 20, 9 ~n
3
) × ~a
left side beam: ~o = p
40
~r = (7~n
1
, 20, 7 ~n
3
) × (~a + ˜n)
right front beam: ~o = p
78
~r = (9~n
1
, 20, 9 ~n
3
) × ~a
right side beam: ~o = p
78
~r = (7~n
1
, 20, 7 ~n
3
) × (~a − ˜n)
Consider a beam ~r originating from ~o, and a vector
~p capturing the difference from ~o to a (road) particle
i, that is, ~p = p
i
−~o. Then, the beam hits the particle
i, if k~p − (
~p•~r
k~rk
)
~r
k~rk
k <
√
1.5 holds.
The steering technique is captured by the reaction
function for the wheel particles. The reaction func-
tions are actually composed of three forces: gravity,
friction, and steering forces. Formally, the reaction
function for the left wheel particle i is stated using a
control force variable θ
i
as the sum of the three forces:
R
i
(p, v, m)
= (0, −0.32, 0)
− 0.02h∃k > 79 : kp
k
− p
i
k < 2iv
i
+ θ
i
norm((p
i
− p
40
) × (p
45
− p
40
))
Here, θ
i
captures a bounded control force with re-
spect to a desired momentum φ
i
:
θ
i
= max(−10, min(φ
i
, 10))
The desired momentum, φ
i
, is computed with re-
spect to the goal direction, ω
l
, and the current direc-
tion, ς, of the left wheel based on the current momen-
tum as:
φ
i
= −20ω
l
+ hω
l
6= 0i
ς
20
19
X
k=0
kv
40
− v
k
k
The goal direction, ω
l
, is obtained from Table 1.
The current direction, in turn, is computed by com-
paring the velocities of the wheel particles headed for-
ward, σ(k), to all of the wheel particles:
ς =
1,
P
19
k=0
(2σ(k) − 1)v
(i,2)
< 0
−1, else
Here, the function σ(k) is computed with re-
spect to the topmost wheel particle, τ , for which
max
19
k=0
(p
(k,2)
) = p
(τ,2)
, and to the lowest wheel
particle, β, for which min
19
k=0
(p
(k,2)
) = p
(β,2)
, as:
σ(k) = (hτ > β ∧ k > τi + hτ > β ∧ k < βi)
· hτ < β ∧ τ < k ∧ k < βi
The steering for the right wheel is analogous to the
steering of the left wheel presented above.
5 MOTION ON ROUGH ROAD
We study the motion of Inchworm and Roller on
Rough Road. Rough Road is a narrow uneven path,
having also variation in altitude. Rough Road con-
sists of 1800 immobile particles. Thus, the shape is
exhaustively captured by the initial positions. Techni-
cally, Rough Road consists of 60 circles, each having
30 particles, as observable in Figure 3. For Rough
Road, we identify the a road particle i with road(i) =
h100 ≤ i < 1900i. Let i be a road particle, that
is road(i) = 1. Also, let α = (i − 100) div 30,
β = (i − 100) mod 30, and γ =
1
30
π. Then, the ini-
tial positions are captured:
p
0
i
= (8, 0.5(α mod 2), 8)
+hα > 30i(0,
1
6
α, 0) + hα ≤ 30i(0, (11 −
1
5
α), 0)
+30(cos(0.5αγ), 0, sin(αγ)) + 8(cos(2βγ), 0, sin(2βγ))
PLAUSIBLE MOTION SIMULATION: INCHWORM VS. ROLLER
73
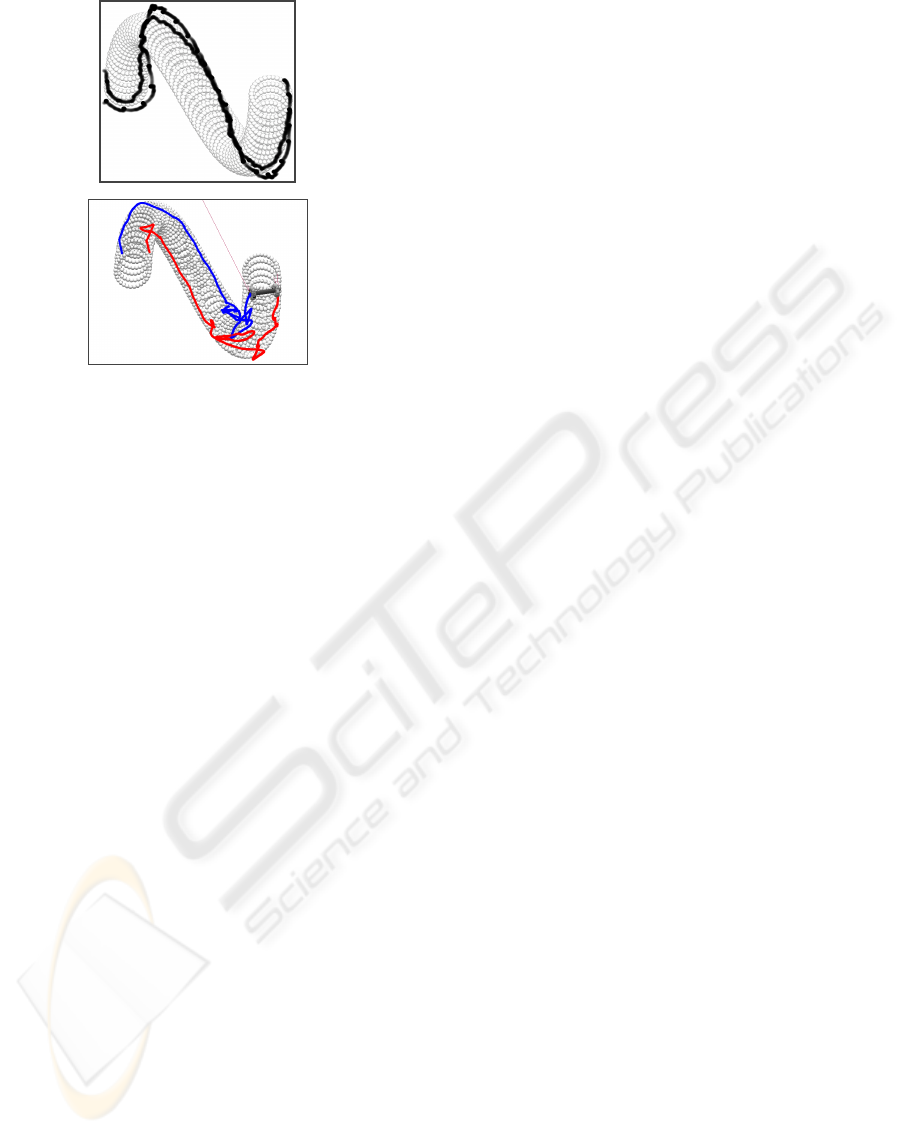
Figure 3: Inchworm (top) and Roller (bottom) on Rough
Road. Travelling direction is from left to right.
As the easiest road for both entities is a flat straight
road, Rough Road offers many challenges; the shape
varies in all dimensions and the surface is bumpy.
The motion of Inchworm is orientation indepen-
dent, and it makes no predictions of the road ahead. It
has a tendency to go straight forward and follow the
edges of the road.
Road altitude variations are problematic for
Roller. As the observation beams are directed to a
constant downward angle, Roller has tendency to un-
dersteer and oversteer in downhills and uphills. Roller
tries to make predictions of the road ahead and keep
both wheels in a safe distance from the edges. In this
respect, Rough Road is wide enough. Roller is suc-
cessful in the first curve, and the problems in the sec-
ond curve are the result of the rough surface.
Contrary to Inchworm that grips tightly to the road
surface and slides slowly along the surface, only the
undermost wheel particles of Roller touch the road.
Therefore, Roller has problems with bumpy road sur-
face especially in the inner corner of the second curve,
where the road elevates sharply.
Figure 3 shows that Roller has a more mechanis-
tic motion than Inchworm. Also, Roller finds its way
forward by trial and error, whereas Inchworm edges
forward smoothly but stubbornly.
6 DISCUSSION
In this paper we studied the use of a specific particle
system in motion simulation. The novelty of the par-
ticle system is that, with it, everything is formalized
systematically and uniformly with matrices.
The results of this study were twofold: First, we
demonstrated the applicability of the particle system
in simulating plausible motion dynamics. Secondly,
we examined the reusability of components that were
formalized using the particle system. In this paper, we
demonstrated the behavior of Inchworm and Roller.
They displayed very different motion dynamics.
The results of this paper complement our ear-
lier results (Holopainen and R
¨
onkk
¨
o, 2006; R
¨
onkk
¨
o,
2006b). In particular, the reusability results encour-
age us to find out what kind of interactive tools and
techniques could be used for shaping and formalizing
particle system components.
We used Atoms (R
¨
onkk
¨
o, 2006a) for computing
the simulations in this paper. Currently, Atoms is not
adequate for running large models. Thus, an impor-
tant topic for future research is to find out how to im-
prove the performance of Atoms.
ACKNOWLEDGEMENTS
We wish to thank Vivian Michael Paganuzzi, as well
as members of Garry Wong’s laboratory.
REFERENCES
Eberhardt, B., Weber, A., and Strasser, W. (1996). A
fast, flexible, particle-system model for cloth draping.
Computer Graphics and Applications, 16(5):52–59.
Holopainen, J. and R
¨
onkk
¨
o, M. (2006). Embedding control
into a particle system: a case study. In Proceedings of
the Ninth IASTED International Conference on Intel-
ligent Systems and Control, pages 92–97. Acta Press,
Anaheim.
Miller, G. (1988). Motion dynamics of snakes and worms.
Computer Graphics, 22:169–178.
R
¨
onkk
¨
o, M. (2006a). Atoms: software development kit.
Department of Computer Science, University of Kuo-
pio. http://www.cs.uku.fi/research/GPL/atoms.tar.
R
¨
onkk
¨
o, M. (2006b). Hybrid systems: Modeling and anal-
ysis using emergent dynamics. Accepted to Nonlinear
Analysis: Theory, Methods & Application s.
Wejchert, J. and Haumann, D. (1991). Animation aero-
dynamics. In Proceedings of the 18th Annual Con-
ference on Computer Graphics and Interactive Tech-
niques, pages 19–22. ACM Press, New York.
Witkin, A. (1997). Physically Based Modeling: Principles
and Practice. Online Siggraph ’97 Course notes.
Wojtan, C., Mucha, P., and Turk, G. (2006). Keyframe
control of complex particle systems using the ad-
joint method. In Proceedings of ACM SIG-
GRAPH/Eurographics Symposium on Computer An-
imation, pages 15–23.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
74
