TILING THE SPHERE WITH DIAMONDS

FOR TEXTURE MAPPING

John E. Crider

32919 Leafy Oak Court, Magnolia TX 77354-6566 USA

Keywords: Coordinate system, mapping, quadrilateral, sphere, texture, tiling.

Abstract: The sphere can be covered by any of an infinite number of tiling sets of equilateral spherical quadrilaterals

(diamonds). Five of these tiling sets have practical use for texture mapping application. Points on the sphere

can be described by intersections of geodesics, which provide coordinate values in a new coordinate system,

defined for each tiling set. Each of the diamonds can be subdivided by a grid of coordinate geodesics to

pixel level and so can be directly mapped to and from a texture array. The diamonds can also be subdivided

into spherical quadrilaterals that can be approximated by pairs of triangles for fast rendering in a graphics

system. Because coordinates in the new system are readily converted to and from Cartesian coordinates,

diamonds can be used easily in interactive graphics and ray-tracing applications.

1 INTRODUCTION

Texture mapping is essentially the mapping of an

image onto the surface of a graphics object. The

image is typically a square array of discrete elements

called texels. In this paper, a texel is also the

quadrilateral on the surface of the sphere that

corresponds to an element in the texture array.

The image also has its own coordinate space,

usually with coordinates denoted as (u, v). The

coordinates typically run from 0 to 1; in this way,

the number of elements in the array (i.e., the

resolution) can be changed without affecting the

mapping mathematics.

A necessary part of texture mapping is the

mapping function, through which a point on the

surface of the object (expressed perhaps in Cartesian

coordinates in object space or in a surface coordinate

system) is mapped to a point in the coordinate space

of the texture image (Foley, van Dam, Feiner, and

Hughes, 1996; Heckbert, 1986).

Watt and Watt (1982) discuss texture mapping in

general and texturing the sphere specifically. The

discussed technique divides the surface of the sphere

into areas that are delimited by circles of constant

latitude and longitude. However, such areas do not

lead to a consistent set of tiles; in particular, polar

areas usually require special treatment.

One common approach to texturing a sphere is to

use a texture array in which the rows correspond to

latitude and the columns correspond to longitude.

This single-tile approach has several disadvantages.

The texels at the poles are extremely small in area, a

waste of texture resources. Further, a graphics

engine that limits the size of texture arrays would

prevent the increase in size of the texture array to

achieve high resolution.

Texturing a sphere through a set of tiles provides

several advantages. First, because each tile covers a

relatively small portion of the spherical surface, it

can have low area distortion and thus can make

economic use of texture resources. Second, a set of

tiles, with a separate texture array mapped to each

tile, can obviously provide higher resolution than

can a single texture array mapped to the whole

sphere. This advantage is especially important with

graphics engines that have restraints on sizes of

texture arrays affecting performance.

The goal here is to cover the sphere with tiles of

identical size and shape such that a texture array can

be easily mapped to each tile. High resolution is

another desirable goal.

The literature on spherical tilings does not

address texture mapping, and the various schemes

described are intended for other applications and are

not usually well suited to texture mapping.

For example, Borgefors (1992) describes a

spherical tiling in which the application is a view-

sphere for image analysis. Each hemisphere is

divided into four tiles of equal area; each tile is then

116

E. Crider J. (2007).

TILING THE SPHERE WITH DIAMONDS FOR TEXTURE MAPPING.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 116-123

DOI: 10.5220/0002074701160123

 SciTePress

recursively divided into four. Each level includes

polar tiles with circular borders, figures that are

difficult to map to texture arrays. At any subdivision

level, the tiles are equal in area but quite different in

shape.

One well-known approach to tiling the sphere is

to begin with the tiling set of twenty equilateral

spherical triangles based on the vertices of an

inscribed regular icosahedron. Finer triangulations

are then obtained by recursively subdividing the

spherical triangles into four with geodesics (Pottman

and Eck, 1990; Ramaraj, 1986). An inscribed

tetrahedron has also been used (Nielson, 1993;

Renka, 1984). The common application for these

tilings is data interpolation.

A similar approach of recursive triangulation is

based on an inscribed regular octahedron (Dutton,

1999); the application is GIS. The hierarchical

coordinate system described is a quad-tree encoding,

not a traditional coordinate system with continuous

coordinates. The recursive subdivisions are based on

latitude and longitude, not geodesics. Other GIS-

related tilings include an equal-area hierarchical

tiling (Wickman, Elvers, and Edvarson, 1974) based

upon a dodecahedron and a tiling (White, Kimerling,

and Overton, 1992) based upon a truncated

icosahedron, or “soccer ball.”

However, when applied to texture mapping, a

recursive triangulation approach has two problems.

First, when the triangular tiles are subdivided to

texel level, the texel figures are triangular and in a

triangular pattern, and are difficult to match with

elements in a square texture array. Conceptually,

there appears to be a simple solution: adjacent

triangular icosahedral tiles can be paired to form a

tiling set of ten quadrilaterals, and the texel triangles

can be similarly paired, forming a matchable pattern

of quadrilateral texels in a quadrilateral grid.

However, in application, recursive triangulation is

essentially the traversal of a quad-tree structure, and

adjacent texel triangles to be paired may be widely

separated in the tree, which can lead to a

complicated scheme for associating these triangles.

Borgefors (1992) states that the recursive

triangulation from icosahedral vertices does not

provide an easy way to determine in which sub-tile

an arbitrary point is located. (This determination is a

complicated recursive calculation involving

numerous geodesics.) Thus, the second problem is

that recursive triangulation lacks a convenient

mapping of arbitrary points from object space to

texture image space; it is not suitable for texture

mapping.

Another approach (Giraldo, 2001) from

icosahedral spherical triangles is to connect the

center of each triangle with the center of each of the

edges, thus forming three spherical quadrilaterals.

The quadrilaterals have two opposite angles of 90°;

the other two angles are 120° and 72°. The

application is fluid dynamics modelling. The

described mapping is through the gnomonic map

projection.

Górski et al. (2005) describe several quadrilateral

tilings derived from the cylindrical equal-area map

projection; sub-tilings are also equal-area. However,

the quadrilaterals in a tiling set are not of the same

shape. Also, polar quadrilaterals require separate

treatment. Designed for processing astronomical

data, this approach reduces the number of latitudes

on which pixels are centered, a concern that is not

relevant for texturing.

One useful technique for texturing the sphere

through tiling is based on Fuller’s map projection

(Gray, 1995). This patented (Fuller, 1946) projection

uses geodesics on polyhedral faces. Although the

patent describes spherical tiles based solely upon the

six square faces and eight triangular faces of the

cuboctahedron, the most common projection is

based on icosahedral spherical triangles. Unlike the

recursive triangulation approach, this technique uses

only geodesics that connect two edges of the original

icosahedral triangles. Such geodesics form the basis

of the map projection, which provides the mapping

from object space to texture image space that is

necessary for texture mapping. This technique’s low

area distortion and triangular tiles make it practical

for texturing the sphere. However, this technique has

a minor disadvantage: the reverse map projection

(i.e., from plane to sphere) has not been developed.

Thus, determining the locations of the texels on the

spherical surface is difficult.

The work reported here starts from the geodesics

that connect two edges of the square tiles as

discussed with the patented Fuller map projection, as

well as from the pairing of icosahedral triangles to

form quadrilaterals as discussed above.

2 THE DIAMOND

In this paper the diamond (equilateral spherical

quadrilateral) is examined as a basis for texturing the

sphere for two reasons.

First, diamonds are versatile in forming tiling

sets. Spherical icosahedral triangles, when paired,

yield a tiling set of diamonds; projected edges of an

TILING THE SPHERE WITH DIAMONDS FOR TEXTURE MAPPING

117

inscribed cube form another. Indeed, there are an

infinite number of diamonds tiling sets.

Second, diamonds and texture arrays are similar

in the sense that both can be perceived as two

dimensional entities, and sizes in both dimensions

are the same. Thus, diamonds appear to be well

suited as mapping targets of textures.

Focusing on the diamond leads to a new

spherical coordinate system, which is based upon

intersections of geodesics within a diamond. It is

general-purpose, its coordinates can be easily

converted to and from Cartesian coordinates, and it

has a variety of potential applications. It is used here

to determine precisely the locations of the texels.

Diamonds can be subdivided to texel level so that

the texels of a texture array can be mapped readily to

and from the texel figures on the spherical surface.

3 INFINITE FAMILIES OF

TILING SETS

Consider a regular hexahedron (cube) inscribed in a

unit sphere. When its edges are projected to the

sphere, the sphere is tiled with a set of six diamonds.

This tiling set may be called a spherical cube.

In this tiling set, one of the vertices can be

chosen as the north pole. It is seen that three of the

tiles touch the north pole; the other three touch the

south pole. Instead of three diamonds sharing a pole,

any greater number of diamonds can share the north

pole, with the same number of diamonds sharing the

south pole. Such a tiling set is a member of an

infinite family of tiling sets. The first few members

of this family are shown in Figure 1.

As the number of diamonds increases, the small

vertex angles decrease and the large vertex angles

increase. For the tiling set of twelve diamonds, the

large vertex angle is 150°. Such a large vertex angle

may cause problems for intersections of geodesics

used for determining texel locations (as discussed in

Sections 5 and 6), so the use of this or larger tiling

sets in the family is not recommended. The

following section describes an alternative tiling set

of twelve diamonds with better geometric

characteristics. Thus only the first three members of

this family are judged to have practical use with

texturing; these three are in the foreground of Figure

The spherical cube may be considered as an

alternative to the common single-tile latitude-

longitude technique described in Section 1. When

tiled spheres covered by the same total number of

texels are compared, the tiling set of six has the

advantages of a narrower range of texel areas and a

smaller maximum texel area (i.e., higher resolution).

The tiling set of eight diamonds provides slightly

higher resolution. This tiling set has no relation to a

regular polyhedron.

The tiling set of ten diamonds is a reasonable

compromise between simplicity of implementation

and high resolution for a given texture array size. Its

vertices are identical to those of an inscribed regular

icosahedron.

Figure 1: Members of an Infinite Family of Tiling Sets.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

118

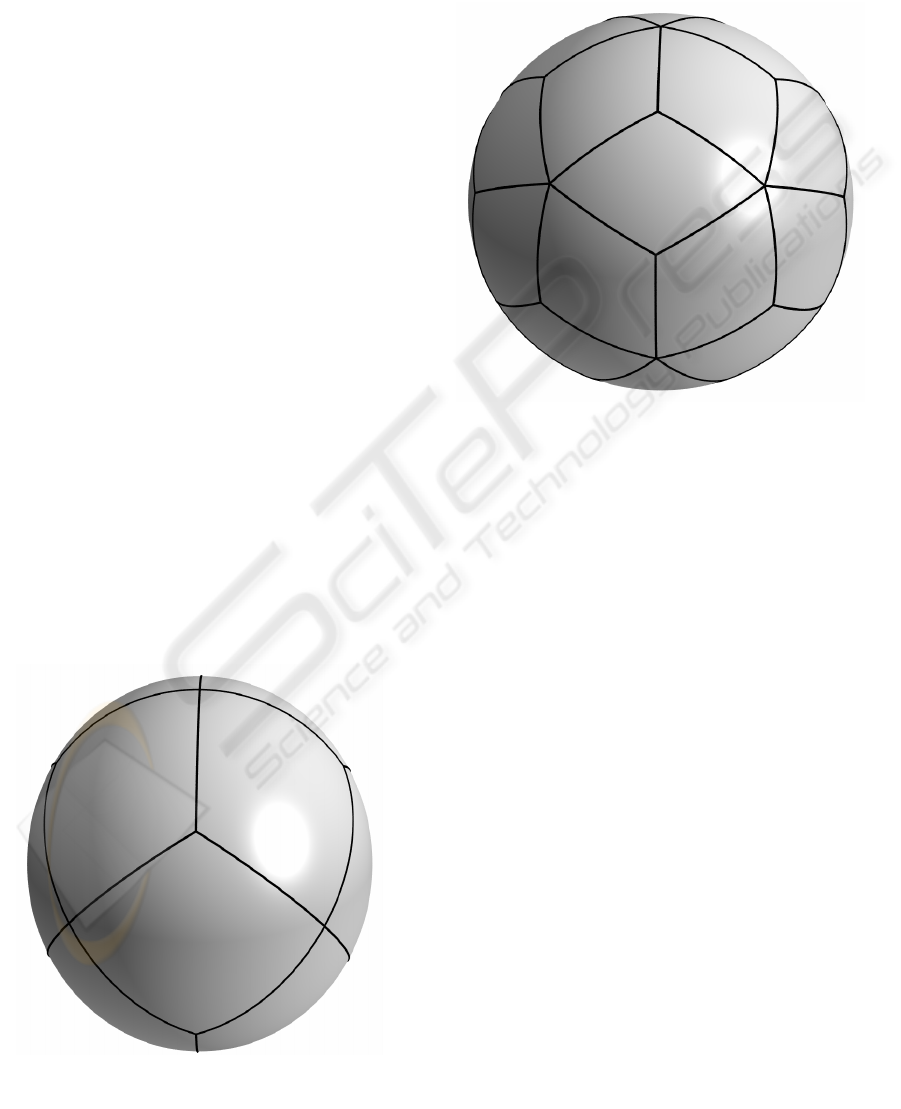
Figure 3: A Tiling Set of Thirty Diamonds.

Figure 2: A Tiling Set of Twelve Diamonds.

There is another infinite family of tiling sets. Its

members can be derived from members of the first

family by a simple transformation. For any tiling set

in the first family that has an odd number of

diamonds touching a pole, a cap on the side of the

sphere that is composed of almost half of the

diamonds is rotated almost 120° to produce a new

tiling set. This tiling set has a mirror image that is

also a member of this family. A tiling set in the first

family that has an even number of diamonds at a

pole has no corresponding member in the second

family. The spherical cube is a member of this

family but is a special case: the transformation

produces the same spherical cube, and the mirror

image is no different.

The only unique member of this family that may

have practical use with texturing is the tiling set of

ten, but it provides no specific advantage. This

family is described here only for completeness;

These two infinite families and the family described

in the following section include all diamond tiling

sets (Ueno and Agaoka, 2002).

4 THE FAMILY OF THREE

TILING SETS

For the first infinite family of tiling sets discussed

above, each non-polar vertex is shared by three

diamonds, and at each of these vertices are two

small vertex angles and one large vertex angle. In

the third family of tiling sets, at each vertex shared

by three diamonds all three vertex angles are large.

Thus, for the diamonds in these tiling sets, each

large vertex angle is 120°. Clearly, the spherical

cube is a member of this family as well. This family

has two other members.

The second member is a tiling set of twelve

diamonds; four diamonds surround each of the poles

and four diamonds ring the equator. This tiling set is

shown in Figure 2.

The third member is a tiling set of thirty

diamonds. Ten of the diamonds are centered on the

equator, and a ring of five diamonds lies between the

equatorial diamonds and each set of five polar

diamonds. This tiling set is appropriate for

applications requiring fine detail; for a given texture

array size, it provides the highest resolution of the

five tiling sets. This tiling set is shown in Figure 3.

5 DIAMOND COORDINATE

SYSTEM

The diamond coordinate system is a new coordinate

system that is based on geodesics and on the tiling

sets of diamonds. This coordinate system is

especially useful for textures on a sphere; it can

identify precisely the location of each texel on the

sphere’s surface. For any point feature on a sphere, it

can identify the texel containing the feature.

This system has three components, represented

as {d, u, v}. The first component, d, is an integer that

identifies one of the diamonds in a specific tiling set

(diamond identifiers may be assigned arbitrarily).

Thus, each tiling set has a different diamond

coordinate system. The specific tiling set being used

is assumed to be known by context.

TILING THE SPHERE WITH DIAMONDS FOR TEXTURE MAPPING

119

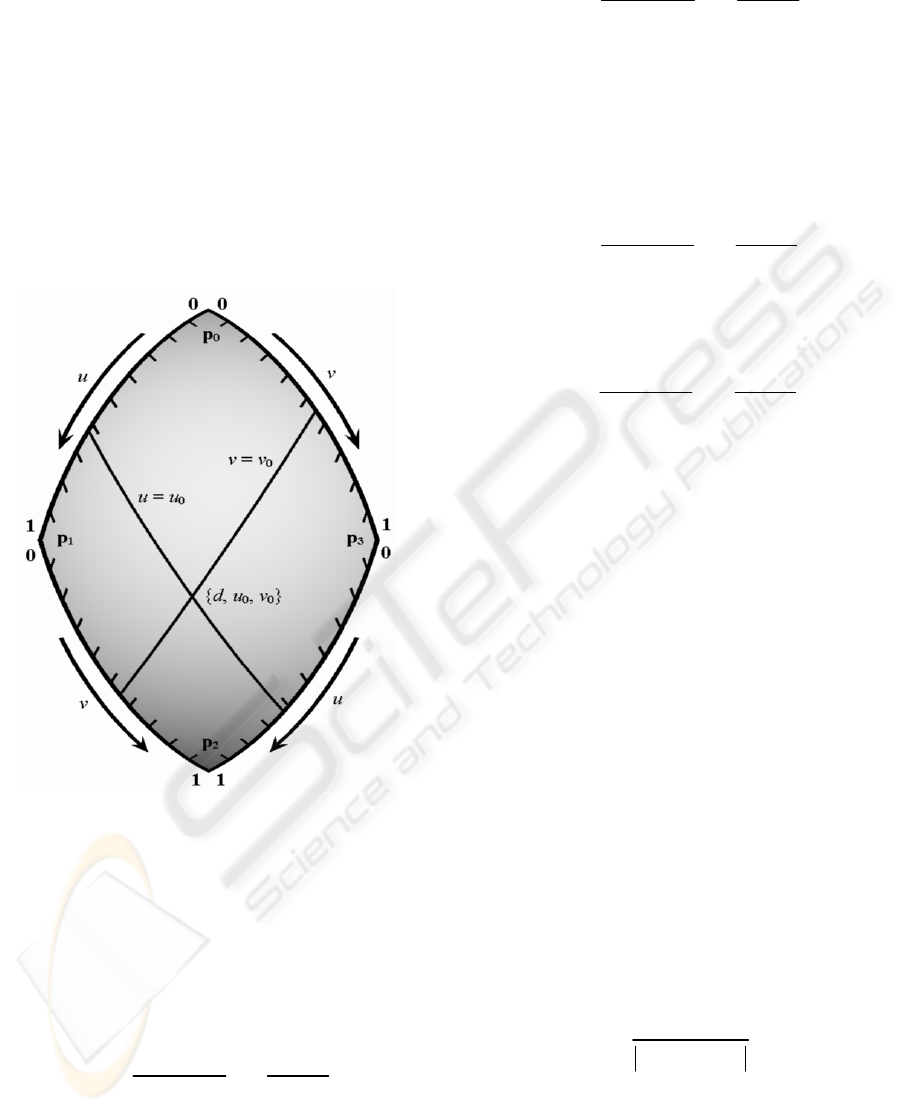
Figure 4: Diamond Coordinate System.

The second and third components of the diamond

coordinate system, u and v, identify a point on the

designated diamond by specifying two geodesics

that intersect at the point.

The u and v coordinates depend upon the four

vertices of the diamond. For each diamond, one of

the vertices with a small angle is designated as p

;

the other vertices are designated as p

, p

, and p

, in

counter-clockwise order. The other small angle is at

, and the large angles are at p

and p

. (Position

vectors are used to represent surface points; the

origin is at the center of the sphere.)

Each of the u and v coordinates ranges from 0 on

one edge of the diamond to 1 on the opposite edge.

Figure 4 illustrates the diamond coordinate system;

in this figure, u

and v

represent arbitrary constants.

Along edge p

-p

of the diamond, coordinate u

runs uniformly from 0 at vertex p

to 1 at vertex p

That is, a point on this edge can be expressed as a

spherical linear interpolation of the two vertices:

00 1

sin( ) sin( )

() .

sin( ) sin( )

SuS uS

−

=+pp p

(1)

The parameter S is the arc length of the edge of the

diamond.

Similarly, along edge p

-p

, coordinate u runs

uniformly from 0 at p

to 1 at p

. A point on this

edge can be expressed as:

13 2

sin( ) sin( )

() .

sin( ) sin( )

SuS uS

−

=+pp p

(2)

The locus of points with a given value of u is

defined to be the geodesic that connects the point

with the value of u on edge p

-p

with the point that

has the same value of u on edge p

-p

Along edge p

-p

of the diamond, coordinate v

runs uniformly from 0 at vertex p

to 1 at vertex p

A point on this edge can be expressed as:

00 3

sin( ) sin( )

() .

sin( ) sin( )

SvS vS

−

=+pp p

Along edge p

-p

, coordinate v runs uniformly

from 0 at vertex p

to 1 at vertex p

. A point on edge

-p

can be expressed as:

11 2

sin( ) sin( )

() .

sin( ) sin( )

SvS vS

−

=+pp p

The locus of points with a given value of v is

defined to be the geodesic that connects the point

with the value of v on edge p

-p

with the point that

has the same value of v on edge p

-p

A geodesic plane is conveniently specified by its

normal vector. With the convention that the normals

of the geodesic planes for constant u point in the

direction of increasing u, the normal of the geodesic

plane for a given u is:

() () () .

uuu

uuu=×npp (3)

Similarly, the normal of the geodesic plane for a

given v is:

() () () .

vvv

×npp

Specific values of u and v identify the point that

is the intersection of the two geodesic planes at the

surface of the sphere. The normals of the two

geodesic planes (u and v) are multiplied (vector

cross product) to yield the line that is the intersection

of the two planes. The intersection of this line and

the unit sphere is the point of interest. Thus,

Equation (4) converts a point from diamond

coordinates to Cartesian coordinates:

() ()

(,)

() ()

(4)

To obtain diamond coordinates for any point p

on the unit sphere with known Cartesian

coordinates, the first step is to identify the diamond

(coordinate d) that contains the point. The scalar

(dot) product of a point p with the normal of a

geodesic plane indicates the side of the plane on

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

120

which p is located. Thus, point p is located on a

given diamond if this condition is true:

(0)0(1)0

(0) 0 (1) 0 .

•≥∧ •≤∧

•≥∧ •≤

npnp

(5)

If it is not known which diamond contains p, the

above condition can be tested for each diamond until

the correct one is found. If one or more of the dot

products is zero, p lies on an edge or a vertex

common to two or more diamonds.

In each tiling set, the edges of several diamonds

may lie on the same geodesic plane. As an

optimisation, these planes can be identified and used

to determine the diamond containing a point p

through fewer comparisons than implied by

Equation(5).

Points on edges and at vertices have multiple

representations. For example, a vertex that is

common to three diamonds has three coordinate

representations (one for each diamond).

For any point p on a diamond, a geodesic of

constant

u passes through the point. This relation is

expressed as:

() 0 .

u •=np

The value of

u that satisfies this equation is the u

coordinate of the point. Substituting the expression

for the normal from Equation(3), then substituting

the two edge points from Equation (1) and Equation

(2), leads to:

() () ()

tan ( ) tan( )

0 ,

uuu

uS uS•+•+•

ap bp cp

(6)

which is quadratic in tan(uS); the coefficient vectors

for Equation (6) are:

()

0213

cos ( )

cos( )

2sin()cos()

sin( ) ,

sin ( ) .

=×

−×+×

+×

=− ×

+×+×

=×

app

pp pp

bpp

pp pp

cpp

If the point is in the relevant diamond [as

confirmed by Equation (5)], then u is obtained from

the quadratic root of Equation (6) that is between 0

and tan(S).

The value of the v coordinate is obtained in the

same manner, with p

and p

interchanged; the

coefficients are:

(

)

()

02 31

cos ( )

cos( )

2 sin( )cos( )

sin( ) ,

sin ( ) ,

=×

−×+×

+×

=− ×

+×+×

=×

app

pp pp

bpp

pp pp

cpp

and the quadratic equation is:

(

)

(

)()

tan ( ) tan( )

0 .

vvv

vS vS

•

+• +•

ap bp cp

(7)

Thus, for each diamond, there are two sets of

constant vectors (a

, b

, c

and a

, b

, c

) that are

used to obtain quadratic coefficients from a point p.

Therefore, Equation (4) converts from diamond

coordinates to Cartesian coordinates, and Equations

(5), (6) and (7) convert from Cartesian coordinates

to diamond coordinates.

The conversions in Equations (6) and (7) also

underlie the necessary texture mapping function

discussed generally in Section 1 and specifically for

diamonds in Section 6.

The conversion from Cartesian coordinates to

diamond coordinates adds significant capability to

the diamond coordinate system, as an interactive

graphics application illustrates. The screen

coordinates corresponding to a mouse click can be

converted to a ray in the view frustum. The

intersection of this ray with a sphere is a point with

determinable Cartesian coordinates, which can be

converted to diamond coordinates to identify a texel

in a texture array. The same considerations apply to

ray-tracing.

6 SUBDIVIDING DIAMONDS TO

TEXELS

A grid of geodesics of constant u and of constant v

subdivides a diamond into an array of (non-

equilateral) sub-diamonds. Typically the values of u

and v for a grid would be chosen to be equally

spaced, and spaced such that there is a one-to-one

correspondence between the sub-diamond

quadrilaterals and the texture array texels.

Thus, the diamond coordinates u and v are

identical to the texture image coordinates u and v

described in Section 1; the necessary texture

mapping function is the identity function [as is

usually true also for parametric surface patches

(Foley et al. 1996; Watt and Watt, 1992)].

TILING THE SPHERE WITH DIAMONDS FOR TEXTURE MAPPING

121

Figure 7: Sphere Textured with the Tiling Set of Thirty;

n = 256.

Figure 6: Sphere Textured with the Tiling Set of Thirty;

n = 16.

Figure 5: Sphere with Tiling Set of Thirty; n = 4.

For a grid of equally-spaced subdivisions, an

important parameter is the number of sub-diamonds

on each side of a diamond; this number is designated

here as n. This number can be any positive integer,

but is typically a power of 2, following from texture

array sizes.

Figure 5 shows the tiling set of thirty with

diamonds subdivided by geodesics of constant u and

v. For illustrative purposes, each diamond has four

sub-diamonds on a side. Graphics systems

commonly have an optimum size for texture arrays;

256 pixels on each side are probably a minimum for

practical use. As is discussed in Section 7, a smaller

number of subdivisions can be useful for other

purposes.

Figure 6 shows a textured sphere with the tiling

set of thirty; each diamond has 16 sub-diamonds on

a side (thus, each texture array is 16x16). Many of

the individual texels are clearly visible; with

reference to Figure 5, various diamond vertices can

be located.

As high resolution is a desirable goal, Figure 7

shows the same textured sphere with the same tiling

set as Figure 6, but each diamond has 256 sub-

diamonds on a side. A sphere textured with any of

the other four tiling sets and with the same texture

array size would not appear noticeably different,

unless the viewpoint were extremely close to the

sphere.

Figure 8 shows the texture array associated with

one of the diamonds of Figure 7. Although the

texture array is square, the rhombic arrangement

shown gives the best planar representation of its

image. This arrangement requires a linear

transformation (skew and rotation) of the u and v

coordinates and is for visualization of a texture array

only; it is not an integral part of the texture mapping.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

122

7 RENDERING WITH

TRIANGLES

For fast animation, curved surfaces are often

approximated by meshes of polygons, usually

triangles. Subdivision of diamonds leads readily to

such an approximation. When the four edges of a

sub-diamond are replaced by line segments, and the

opposite vertices with large angles are connected by

a line segment, the result is a pair of (non-coplanar)

triangles.

Figure 5 serves as an example because it could

have been rendered this way. Each of the 16 sub-

diamonds on a diamond can be approximated by a

pair of triangles. This example would lead to a

sphere approximated by a mesh of 960 triangles.

Thus, spherical diamonds can be subdivided to

various levels for different purposes. At the finest

level of subdivision, the resulting sub-diamonds

correspond to texels. At a coarser level of

subdivision, the sub-diamonds correspond to triangle

pairs for fast rendering through a mesh of triangles.

ACKNOWLEDGEMENTS

Texture arrays used in the colour figures were

derived from the NASA image “The Blue Marble:

Land Surface, Ocean Color, Sea Ice and Clouds”

available online at www.visibleearth.nasa.gov.

Figures 1, 2, and 3 were generated with POV-Ray,

available online at www.povray.org.

REFERENCES

Borgefors, G., 1992. A hierarchical ‘square’ tessellation of

the sphere, Pattern Recognition Letters, 13, 183-188.

Dutton, G. H., 1999. A hierarchical coordinate system for

geoprocessing and cartography, Lecture Notes in

Earth Sciences, Vol. 79, Berlin: Springer-Verlag.

Foley, J. D., van Dam, A., Feiner, S. K., & Hughes, J. F.,

1996. Computer graphics: Principles and practice,

Reading, MA: Addison-Wesley, pp. 741-744.

Fuller, R. B., 1946. US Patent No. 2 393 676.

Giraldo, F. X., 2001. A spectral element shallow water

model on spherical geodesic grids, International

Journal for Numeric Methods in Fluids, 35, 869-901.

Górski, K. M., Hivon, E., Banday, A. J., Wandelt, B. D.,

Hansen, F. K., Reinecke, M., & Bartelmann, M., 2005.

HEALPix: a framework for high-resolution

discretization and fast analysis of data distributed on

the sphere, The Astrophysical Journal, 622, 759–771.

Gray, R. W., 1995. Exact transformation equations for

Fuller’s world map, Cartographica, 32 (3), 17-25.

Heckbert, P. S., 1986. Survey of texture mapping, IEEE

Computer Graphics and Applications, 6 (6), 56-67.

Nielson, G. M., 1993. Modeling and visualizing

volumetric and surface-on-surface data, in H. Hagen,

H. Mueller, & G. M. Nielson, (Eds.), Focus on

scientific visualization (pp. 191-242), New York:

Springer-Verlag.

Pottman, H., & Eck, M., 1990. Modified multiquadric

methods for scattered data interpolation over a sphere,

Computer Aided Geometric Design, 7, 313-321.

Ramaraj, R., 1986. Interpolating scattered data on a

sphere, master’s thesis, Computer Science Dept.,

Arizona State Univ.

Renka, R. J., 1984. Interpolation of data on the surface of

a sphere, ACM Trans. on Mathematical Software, 10,

417-436.

Ueno, Y., & Agaoka, Y., 2002. Classification of the tilings

of the 2-dimensional sphere by congruent triangles,

Hiroshima Math. J., 32, 463–540.

Watt, A. H., & Watt, M., 1992. Advanced animation and

rendering techniques: Theory and practice, Reading,

MA: Addison-Wesley, pp. 179-186.

White, D., Kimerling, J., & Overton, W. S., 1992.

Cartographic and geometric components of a global

sampling design for environmental monitoring,

Cartography and Geographic Information Systems,

, 5-22.

Wickman, F. E., Elvers, E., & Edvarson, K., 1974. A

system of domains for global sampling problems,

Geografiska Annaler, Series A: Physical Geography,

56, 201-212.

Figure 8: A Texture Array (256x256), Skewed and

Rotated, for a Diamond in the Tiling Set of Thirty.

TILING THE SPHERE WITH DIAMONDS FOR TEXTURE MAPPING

123