PYRAMID FILTERS BASED ON BILINEAR INTERPOLATION

Martin Kraus

Computer Graphics and Visualization Group, Technische Universit

at M

unchen, Germany

Magnus Strengert

Visualization and Interactive Systems Group, Universit

at Stuttgart, Germany

Keywords:

Signal processing, image processing, multi resolution, pyramid algorithm, graphics hardware.

Abstract:

The implementation of several pyramid methods on programmable graphics processing units (GPUs) in recent

years led to additional research interest in pyramid algorithms for real-time computer graphics. Of particular

interest are efﬁcient analysis and synthesis ﬁlters based on hardware-supported bilinear texture interpolation

because they can be used as building blocks for many GPU-based pyramid methods. In this work, several new

and extremely efﬁcient GPU-implementations of pyramid ﬁlters are presented for the ﬁrst time. The discussion

employs a new notation, which was developed for the consistent and precise speciﬁcation of these ﬁlters and

also allowed us to systematically explore appropriate ﬁlter designs. The presented ﬁlters cover analysis and

synthesis ﬁlters, (quasi-)interpolation and approximation, as well as discontinuous, continuous, and smooth

ﬁlters. Thus, a toolbox of ﬁlters and their efﬁcient implementations for a great variety of GPU-based pyramid

methods is presented.

1 INTRODUCTION

Many techniques in real-time image processing em-

ploy the pyramid algorithm by Burt (Burt, 1981), and

GPU-based image processing is no exception to this

rule (Williams, 1983; Kr

uger and Westermann, 2003;

Lefebvre et al., 2005; Strengert et al., 2006). Pyramid

methods are of particular interest because they usu-

ally feature a linear time complexity and require only

a limited number of switches of the render target.

Although modern GPUs offer an enormous ras-

terization performance, the actual rasterization budget

for each pixel often consists of the equivalent to only

a few dozens of texture reads. This is already a seri-

ous limitation for many image processing techniques,

which often employ large two-dimensional convolu-

tion ﬁlters. Thus, even GPU-based implementations

of complex image processing techniques are often re-

stricted to small image sizes and/or low frame rates.

Therefore, several very efﬁcient techniques have been

developed to implement speciﬁc (often small) con-

volution ﬁlters on GPUs (Sigg and Hadwiger, 2005;

Green, 2005). Unfortunately, many of these tech-

niques are restricted to very speciﬁc ﬁlters and partic-

ular applications; thus, the efﬁcient implementation of

many other ﬁlters is still a challenging task in GPU-

based image processing.

In this work, we generalize a recently published

technique (Strengert et al., 2006) for a 2×2 box anal-

ysis ﬁlter and a 2 × 2 B-spline synthesis ﬁlter. By

formalizing the underlying concept with the help of a

new notation, we are able to systematically explore

appropriate ﬁlter designs and present several ﬁlters

that can be more efﬁciently implemented on GPUs

using bilinear texture interpolation than previous pub-

lications suggested.

In order to make these ﬁlters and their imple-

mentations more easily accessible to readers who

are looking for particular ﬁlters, we have also in-

cluded some previously published ﬁlter implementa-

tions. Moreover, these ﬁlters should help to illustrate

our new notation and the systematic ﬁlter construction

suggested in this work. We classify ﬁlters as basic

ﬁlters presented in Section 3; i.e., convolution ﬁlters

without reduce or expand operation; analysis ﬁlters

presented in Section 4; i.e., convolution ﬁlters com-

bined with a reduce operation; and synthesis ﬁlters

presented in Section 5, which are combined with an

Kraus M. and Strengert M. (2007).

PYRAMID FILTERS BASED ON BILINEAR INTERPOLATION.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 21-28

DOI: 10.5220/0002076300210028

 SciTePress

H0L

= h

synthesis



H1L

= h

analysis

H0L

top of pyramid: g

H2L

(a)

image g

2´2

Ä g

filter h

2´2

(b)

2×2

⊗ g =



1,1

1,2

2,1

2,2



⊗





1,1

1,2

2,1

2,2

0 0 0





≡





0 0 0

0 h

1,1

1,2

0 h

2,1

2,2





⊗





1,1

1,2

2,1

2,2

0 0 0









1,1

1,2

1,1

+ h

1,1

1,2

2,1

1,1

+ h

1,1

2,1

2,2

1,1

+ h

2,1

1,2

+ h

1,2

2,1

+ h

1,1

2,2

1,2

+ h

1,2

2,2

2,1

2,2

2,1

+ h

2,1

2,2





(c)

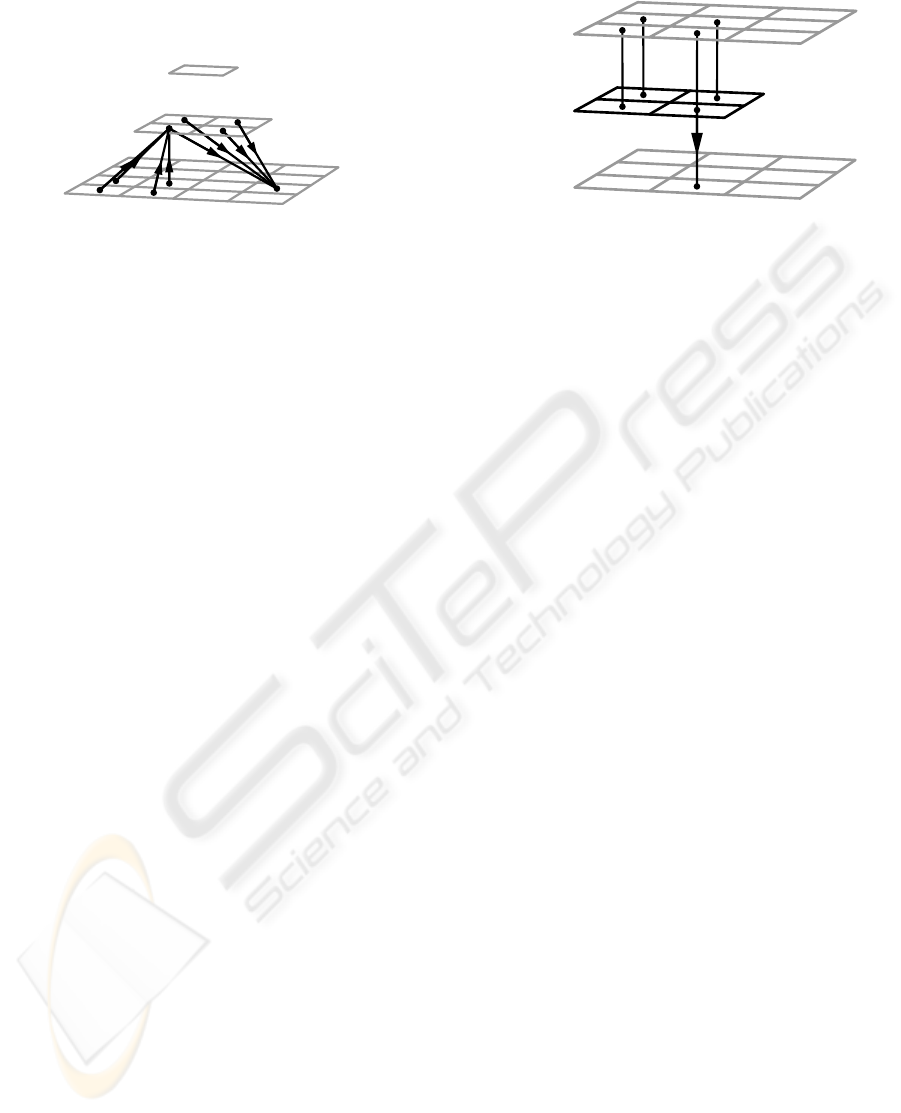
Figure 1: (a) An image pyramid consisting of 3 levels: g

(0)

, g

(1)

, and g

(2)

. (b) Illustration of the convolution of a 3× 3 image

g with a 2 × 2 ﬁlter h

2×2

. (c) The formal equation of the convolution illustrated in (b) including the equivalent 3× 3 ﬁlter

padded with zeros. Note the “mirrored” indices of h

2×2

and the “shift” of non-zero components in the resulting matrix.

expand operation. Analysis and synthesis ﬁlters are

further classiﬁed according to their featured smooth-

ness (in the limit of inﬁnitely many reduce or expand

operations). Section 6 concludes this work with our

plans for future work.

2 PYRAMID METHODS ON GPUS

Pyramid methods usually convolve image data of one

pyramid level with a small analysis ﬁlter and reduce

the resulting image data to compute coarser pyramid

levels. This process is called analysis while the op-

posite process, called synthesis, expands image data

and convolves it with small synthesis ﬁlters to com-

pute ﬁner pyramid levels; see Figure 1a. The reduce

and expand operation are also called downsampling

and upsampling, respectively.

Pyramid methods—more speciﬁcally spoken,

pyramid images—have been most successful in com-

puter graphics in the form of mipmap textures as

proposed by Williams (Williams, 1983). More re-

cently, the possibility to read pixel data of a raster-

ized image by texture interpolation without crucial

overhead led to new real-time image processing tech-

niques on GPUs (Green, 2005). For pyramid meth-

ods in GPU-based image processing, we suggested to

employ hardware-supported bilinear texture interpo-

lation for the reduce operation combined with a 2× 2

convolution ﬁlter (Strengert et al., 2006). However,

the only analysis ﬁlter presented in that work is a sim-

ple 2× 2 box ﬁlter. For the synthesis, we proposed to

employ bilinear texture interpolation for the combi-

nation of the expand operation and a 2× 2 synthesis

ﬁlter corresponding to the biquadratic B-spline sub-

division scheme (Catmull and Clark, 1978), which is

better known as the Doo-Sabin subdivision scheme

for regular quadrilaterals.

3 BASIC FILTERS

The ﬁlters discussed in this section are simple con-

volution ﬁlters without reduce or expand operation.

Thus, strictly speaking, they are not pyramid ﬁlters.

However, they act as building blocks for the more

complex ﬁlters discussed in Sections 4 and 5. A dis-

crete convolution of a ﬁlter mask h and an image g

resulting in an image f is denoted by

f = h⊗ g.

If the ﬁlter mask h is represented by an n

× n

matrix

and the image g is of dimensions n

× n

, the matrix

component f

r,c

for the row index r and the column

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

index c is deﬁned by:

r,c

∑

i=1

∑

j=1

i, j

r−⌊i−n

/2⌋,c−⌊ j−n

/2⌋

Standard matrix notation is employed; i.e., row and

column indices are given in this order and indices start

with 1. Moreover, matrix products of column vectors

times row vectors (i.e., outer products of vectors) are

employed for separable ﬁlters.

Components of the image g with indices outside

the ranges from 1 to n

and 1 to n

, respectively, are

either set to 0 if the image g represents a ﬁlter mask,

or determined by clamping the indices to the valid

ranges. The dimensions of f depend on the partic-

ular application; in this work we usually determine

the dimensions of f by g’s dimensions; exceptions are

mentioned explicitly.

For even ﬁlter dimensions n

and n

, it is often

useful to think of the pixel positions of image f being

shifted by half a pixel along the diagonal relatively to

image g. In order to make this shift explicit, one can

use zero padding of the convolution mask; e.g., for

a 2× 2 convolution mask h

2×2

there is an equivalent

3×3 convolution mask with zeros in the ﬁrst row and

column:

2×2

def



1,1

1,2

2,1

2,2



≡





0 0 0

0 h

1,1

1,2

0 h

2,1

2,2





For an illustration of these deﬁnitions and the de-

scribed shift of components of f , see Figures 1b and

1c.

As mentioned, g—and therefore f—may also rep-

resent ﬁlter masks. In this case, g and h denote two

convolution masks (applied from right to left), which

can be combined in one convolution mask f. In

fact, the main motivation for our formalism is to de-

compose complex ﬁlter masks (e.g., f ) into multiple

smaller ﬁlters (e.g., h and g, but usually more than

two), which are small enough (i.e., 2×2) to be imple-

mented by bilinear texture interpolations. In this way,

complex ﬁlters can be implemented by a sequence of

bilinear texture interpolations.

3.1 2× 2 Box Filter

The most important building block for the ﬁlters dis-

cussed in this work is the 2× 2 box ﬁlter, also known

as uniform, average, or mean ﬁlter:

2×2

box

def



1 1



Since this ﬁlter multiplies four neighboring pixels

with equal weights, it is easily implementable with

one hardware-accelerated bilinear texture image in-

terpolation. The sampling position for this texture in-

terpolation (usually speciﬁed by texture coordinates)

is determined by the position of the shared corner of

the four pixels (in the “little squares” model of pixels)

or the barycenter of the four pixels (if the pixels them-

selves represent sampling points in a uniform grid).

Due to our deﬁnition of the convolution, the sam-

pling point for the resulting matrix component with

indices r and c is located at the upper, left corner of

the pixel speciﬁed by r and c in the original source

matrix. (We assume a coordinate system that corre-

sponds to traditional matrix notation with the (posi-

tive) r axis pointing downwards and the (positive) c

axis pointing to the right.) This shift by half a di-

agonal of one pixel is more explicit in the equivalent

zero-padded 3 × 3 ﬁlter mask, which will be called

box

2×2

box

≡ h

box

def





0 0 0

0 1 1





The arrow in the symbol h

box

indicates the position

of non-zero elements in the 3 × 3 matrix as well as

the shift of non-zero elements in the resulting matrix

illustrated in Figure 1c. Note, however, that the sam-

pling position for the bilinear texture interpolation is

shifted in the opposite direction relatively to the orig-

inal pixel position.

Obviously, there are further (non-equivalent) zero-

padded 3 × 3 ﬁlters, which shift pixel positions in

other directions; e.g., the opposite direction for the

ﬁlter h

box

def





1 1 0

0 0 0





This ﬁlter h

box

can also be implemented by a bilin-

ear texture interpolation if the sampling point is set

to the opposite (lower, right) pixel corner. These two

box ﬁlters are the only building blocks for all ﬁlters

presented in this section and Section 4; i.e., all these

ﬁlters can be implemented by a decomposition into a

sequence of convolutions with h

box

and h

box

, and the

application of the corresponding sequence of bilinear

texture interpolations. The most basic example is the

3× 3 Bartlett ﬁlter discussed next.

3.2 3× 3 Bartlett Filter

Bartlett ﬁlters are also called triangular or (in partic-

ular in one dimension) triangle ﬁlters. They are sepa-

rable ﬁlters; therefore, they may be decomposed into

PYRAMID FILTERS BASED ON BILINEAR INTERPOLATION

matrix products of column times row vectors. In this

work, the 3× 3 Bartlett ﬁlter is of particular interest:

3×3

Bartlett

def





1 2 1

2 4 2

1 2 1















1 2 1



The separation into two one-dimensional ﬁlters

can also be expressed by a sequence of two convolu-

tions with these ﬁlters (with appropriate ﬁlter dimen-

sions and index mirroring). However, the represen-

tation as a convolution of box ﬁlters leads to a more

efﬁcient implementation:

3×3

Bartlett





0 0 0

0 1 1





⊗





1 1 0

0 0 0





= h

box

⊗ h

box

= h

box

⊗ h

box

I.e., a sequence of two convolutions with h

box

and h

box

is equivalent to a single convolution with the 3 × 3

Bartlett ﬁlter h

3×3

Bartlett

. Therefore, the 3 × 3 Bartlett

ﬁlter may be implemented by a sequence of two bi-

linear texture interpolations corresponding to the two

2 × 2 box ﬁlters. Note that the second texture inter-

polation has to access the result of the ﬁrst convo-

lution; thus, a hardware-accelerated implementation

will usually have to switch the render target in order

to access the previously rasterized image. Note also

that it is crucial to alternate between h

box

and h

box

;

otherwise, the discussed shifts would not cancel and

the resulting image would be shifted by one full pixel

position.

Since the 3×3 Bartlett ﬁlter h

3×3

Bartlett

is particularly

useful, we will also use it for building up more com-

plex ﬁlters. However, it is always understood that a

convolution with h

3×3

Bartlett

is equivalent to a sequence

of one convolution with h

box

and one convolution with

box

3.3 Gaussian Filters

Repeated convolutions of Bartlett ﬁlters are equiva-

lent to approximations of Gaussian ﬁlters if all non-

zero matrix components of the resulting ﬁlters are

considered; for example:

5×5

Gauss

def







1 4 6 4 1

4 16 24 16 4

6 24 36 24 6

4 16 24 16 4

1 4 6 4 1







≡ h

3×3

Bartlett

⊗ h

3×3

Bartlett

7×7

Gauss

def







1 6 15 20 15 6 1

6 36 90 120 90 36 6

15 90 225 300 225 90 15

20 120 300 400 300 120 20

15 90 225 300 225 90 15

6 36 90 120 90 36 6

1 6 15 20 15 6 1







≡ h

3×3

Bartlett

⊗ h

3×3

Bartlett

⊗ h

3×3

Bartlett

The basic reason for the approximation of Gaus-

sian ﬁlters is the central limit theorem; in fact, any

reasonable, positive ﬁlter will converge to a Gaussian

ﬁlter in the limit of inﬁnitely many convolutions. In

the case of the box ﬁlter—and therefore also for the

Bartlett ﬁlter—the continuous convolutions are actu-

ally higher-order B-splines.

Since each convolution with a Bartlett ﬁlter can be

implemented by two bilinear texture interpolations,

n − 1 texture interpolations are necessary to imple-

ment an approximation to the convolution with an

n × n Gaussian ﬁlter. For comparison, a separable

n× n ﬁlter with ﬁxed ﬁlter weights for the two one-

dimensional ﬁlters would require 2n nearest-neighbor

texture reads.

4 ANALYSIS FILTERS

Analysis ﬁlters are convolution ﬁlters that are com-

bined with a reduce operation, which reduces the

number of pixels by a factor of 2 in each dimen-

sion. Therefore, this operation is also called down-

sampling. In our notation it is indicated by a down-

ward pointing arrow:

f = h⊗

↓

which deﬁnes the components of f as:

r,c

∑

i=1

∑

j=1

i, j

2r−⌊i−n

/2⌋,2c−⌊ j−n

/2⌋

The issue of shifts by half a pixel diagonal is dif-

ferent from the problem discussed in Section 3. Since

the number of components is divided by 2, it is prefer-

able to work with even dimensions of images and ﬁl-

ter masks. Moreover, it is often preferable to use sym-

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

metric ﬁlter mask (in the sense of h

= h

−i+1

) in or-

der to avoid asymmetric weighting of even and odd

pixels.

For convenience we introduce a particular nota-

tion for the combination of an analysis ﬁlter with a

reduction by a factor of 2

in each dimension:

f = h⊗

↓

which results in these components of f:

r,c

∑

i=1

∑

j=1

i, j

r−⌊i−n

/2⌋,2

c−⌊ j−n

/2⌋

Our notation combines a reduce operation with a

convolution in a single operation. Thus, if the con-

volution can be implemented with a bilinear texture

interpolation, the combination with the reduce opera-

tion is also implementable with a bilinear texture in-

terpolation. To this end, it is only necessary to use a

sparser grid of texture sampling points.

4.1 Discontinuous Filter

In order to illustrate our notation for analysis ﬁlters,

it is ﬁrst applied to the 2 × 2 box ﬁlter, which is the

standard analysis ﬁlter for mipmap generation:

2×2

box

⊗

↓

g ≡ h

box

⊗

↓

In the case of analysis ﬁlters, the use of h

2×2

box

might be

preferable, although it is equivalent to h

box

. One bilin-

ear texture interpolation is sufﬁcient to implement this

analysis ﬁlter in pyramid methods (Strengert et al.,

2006).

The 2 × 2 box ﬁlter is classiﬁed as “discontinu-

ous” analysis ﬁlter because the equivalent ﬁlter for a

reduction of the dimensions by a factor of 2

is al-

ways a discontinuous box ﬁlter—even in the limit of

m → ∞: Consider the squared ﬁlter, which is deﬁned

by a sequence of two reduce operations and convolu-

tions:



2×2

box



⊗

↓

def

= h

2×2

box

⊗

↓



2×2

box

⊗

↓



Thus, the actual (separable) box ﬁlter is:



2×2

box





0 0 0 1 1 1 1



⊤



0 0 0 1 1 1 1



For a general factor 2

, the equivalent ﬁlter



2×2

box





0. ..0

{z}

×(2

−1)

1. ..1

{z}

×2



⊤



0. ..0

{z}

×(2

−1)

1. ..1

{z}

×2



is still a discontinuous box ﬁlter. The one-

dimensional ﬁlter, which this separable ﬁlter is con-

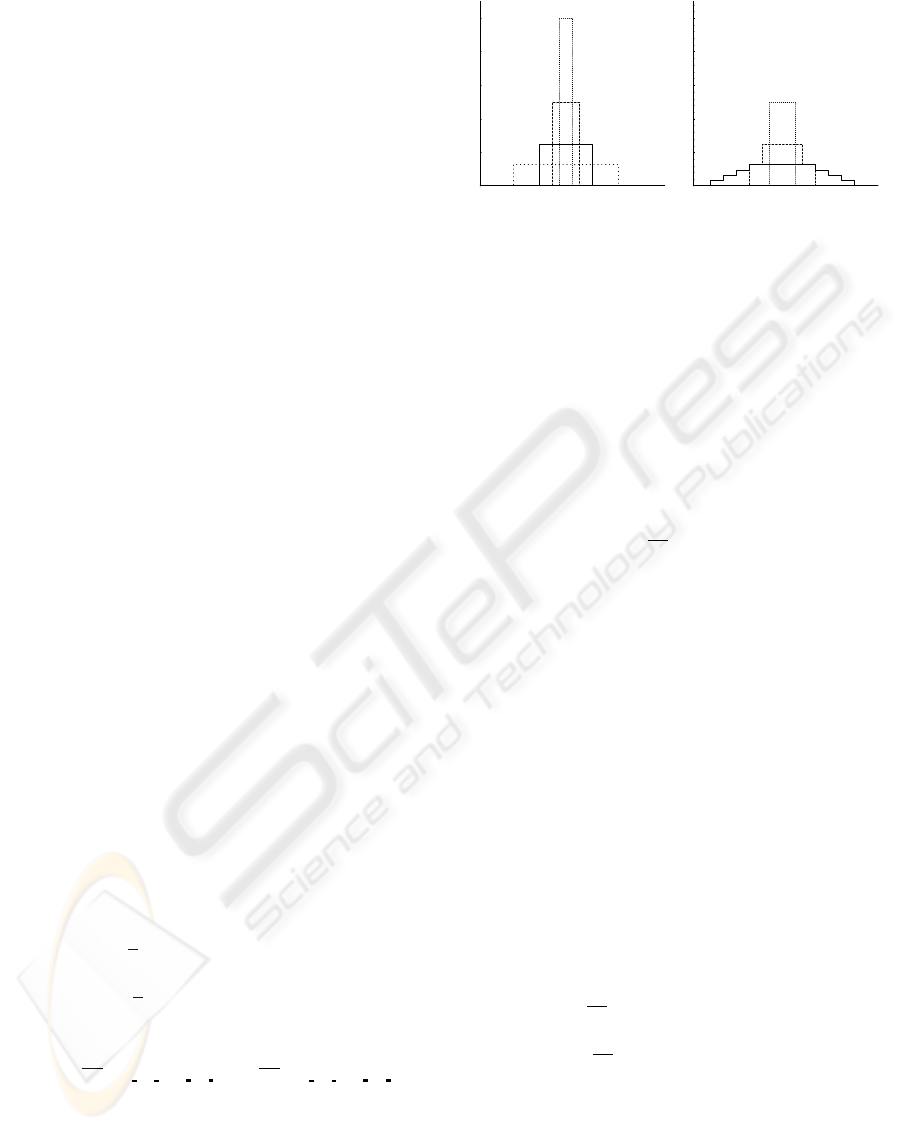
structed from, is illustrated in Figure 2a for various

values of m. The same technique is employed to dis-

cuss and classify the smoothness of all analysis ﬁlters

presented in this section.

0.1

0.2

0.3

0.4

0.5

m = 1

m = 2

m = 3

m = 4

(a)

0.1

0.2

0.3

0.4

0.5

m = 1

m = 2

m = 3

(b)

Figure 2: (a) Powers of the 1D box ﬁlter mask correspond-

ing to h

2×2

box

. (b) Same as (a) for h

4×4

box

4.2 C

-Continuous Filter

While the 2 × 2 box ﬁlter is a discontinuous analysis

ﬁlter, the 4 × 4 box ﬁlter results in a C

-continuous

analysis ﬁlter in the limit of inﬁnitely many analysis

steps. It is deﬁned as:

4×4

box

def







1 1 1 1







4×4

box

⊗

↓

g ≡ h

box

⊗



box

⊗

↓



As indicated by our notation, this ﬁlter can be con-

structed by a reduce operation that includes a convo-

lution with h

box

and a simple convolution with h

box

Therefore, the implementation requires only two bi-

linear texture interpolations. However, there exists

one additional implementation difﬁculty: the ﬁrst re-

duce operation will in general compute non-zero com-

ponents for the 0-th row and column. These interme-

diate results have to be stored and used in the second

convolution, otherwise the components of the ﬁrst

row and column of the total result will be corrupted.

For the discussion of the smoothness of this anal-

ysis ﬁlter, we consider the equivalent (separable)

squared ﬁlter ﬁrst:



4×4

box





0 0 0 0 1 1 2 2 2 2 2 2 1 1 0



⊤



0 0 0 0 1 1 2 2 2 2 2 2 1 1 0



The ﬁrst three powers are illustrated in Figure 2b. In

contrast to the 2 × 2 box ﬁlter, the 4 × 4 box ﬁlter

has overlapping domains and therefore becomes C

continuous in the limit m → ∞; in fact, the 1D ﬁl-

ter becomes piecewise-linear with a linear ascending

part, a constant part, and a linear descending part.

Our notation also suggests the construction of an

PYRAMID FILTERS BASED ON BILINEAR INTERPOLATION

(a) (b)

Figure 3: Pyramid image blurring using (a) the 2 × 2 box

analysis ﬁlter and (b) the 4 × 4 box analysis ﬁlter. (The

employed synthesis ﬁlter is discussed in Section 5.3.).

alternative combination of two box ﬁlters with one re-

duce operation:

3×3

Bartlett

⊗

↓

g ≡ h

box

⊗

↓



box

⊗ g



In the limit of m → ∞ this ﬁlter is also C

-continuous

(in fact, it is a triangle function); however, it includes

an additional undesirable shift and—what is worse—

the analysis of even and odd pixels becomes asym-

metric, which is likely to result in ﬂickering artifacts

in animations. Therefore, the h

4×4

box

ﬁlter appears to be

the preferable C

-continuous analysis ﬁlter; e.g., for

pyramidal image blurring (Strengert et al., 2006) as

illustrated in Figure 3.

4.3 C

-Continuous Filter

By combining one reduce operation and three con-

volutions with box ﬁlters a C

-continuous ﬁlter can

be constructed, which we call h

4×4

quadratic

since it cor-

responds to a biquadratic B-spline in the limit of in-

ﬁnitely many analysis steps. The ﬁlter is deﬁned as

4×4

quadratic

def







1 3 3 1

3 9 9 3

1 3 3 1







4×4

quadratic

⊗

↓

g ≡ h

box

⊗

↓



3×3

Bartlett

⊗ g



The decomposition shows that three bilinear texture

interpolations are sufﬁcient for an implementation of

this analysis ﬁlter.

The squared ﬁlter already indicates a shape similar

to the quadratic B-spline:



4×4

quadratic





0 0 0 0 1 3 6 10 12 12 10 6 3 1 0



⊤



0 0 0 0 1 3 6 10 12 12 10 6 3 1 0



In the limit of inﬁnitely high powers it actually

converges to the C

-continuous biquadratic B-spline

function.

Another combination of three box ﬁlters and one

reduce operation is:

3×3

Bartlett

⊗



box

⊗

↓



;

however, this analysis ﬁlter is only C

-continuous ac-

cording to our classiﬁcation and requires one more

texture interpolation than h

4×4

box

. Yet another combina-

tion is:

box

⊗



3×3

Bartlett

⊗

↓



which results in aC

-continuous analysis ﬁlter but in-

cludes an undesirable shift and an asymmetric weight-

ing of pixels. Thus, h

4×4

quadratic

is usually the preferable

-continuous analysis ﬁlter.

The construction of higher-order B-spline analysis

ﬁlters consists of additional convolutions with 2 × 2

box ﬁlters before the reduce operation is applied, e.g.:

5×5

cubic

⊗

↓

g ≡ h

box

⊗

↓



3×3

Bartlett

⊗



box

⊗ g



5 SYNTHESIS FILTERS

Analogously to analysis ﬁlters, synthesis ﬁlters are

convolution ﬁlters that are combined with an expand

operation, which increases the number of pixels by

a factor of 2 in each dimension. This operation is

also called upsampling and is indicated by a upwards

pointing arrow in our notation:

f = h⊗

↑

where the components of f are:

r,c

∑

i=1

∑

j=1

r mod 2,c mod 2

i, j

× g

⌊(r+1)/2⌋−⌊i−n

/2⌋,⌊(c+1)/2⌋−⌊ j−n

/2⌋

The synthesis ﬁlters presented in this section

are strongly related to popular subdivision schemes,

which are very well known in computer graphics;

thus, we will considerably shorten the discussion by

refering the reader to the corresponding concepts for

subdivision schemes as discussed, for example, by

Zorin et al. (Zorin et al., 2000).

Similarly to the case of analysis ﬁlters, the com-

bination of an expand operation and convolution ﬁl-

ters in our notation is closer to an efﬁcient implemen-

tation using bilinear texture interpolation than tradi-

tional notations. One crucial difference to analysis

ﬁlters is the choice of sampling positions in the corre-

sponding bilinear texture interpolation. For most in-

terpolating synthesis ﬁlters, the sampling points are

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

the centers of pixels, their corners, and the midpoints

of their edges. This corresponds to face-split sub-

division schemes, which are also known as primal

schemes.

The most important alternative sampling posi-

tions are the positions of the Doo-Sabin subdivision

scheme for regular quadrilaterals (Strengert et al.,

2006). This alternative corresponds to vertex-split

subdivision schemes (also known as dual schemes)

and offers the advantage of symmetric computations

for all sampling positions while face-split schemes

distinguish between old and new positions.

In both cases, there are four different kinds of

sampling positions, which correspond to four convo-

lution ﬁlters h

1,1

, h

1,0

, h

0,1

, and h

0,0

with the super-

scripts determined by the new row index modulo 2

and the new column index modulo 2. This notation

is illustrated with the help of the well-known synthe-

sis ﬁlters for nearest-neighbor interpolation, bilinear

interpolation, and the biquadratic B-spline ﬁlter. On

the other hand, the suggested implementation of the

bicubic B-spline synthesis ﬁlter and the construction

of higher-order synthesis ﬁlters is a new result.

5.1 Discontinuous Filter

A discontinuous synthesis ﬁlter is already provided by

nearest-neighbor texture interpolation; thus, it is not

of particular interest for our work. However, we have

included it here for completeness and to demonstrate

our notation for this very basic synthesis ﬁlter:

1,1

nearest

def

= h

1,0

nearest

def

= h

0,1

nearest

def

= h

0,0

nearest

def





0 0 0

0 1 0

0 0 0





5.2 C

-Continuous Filter

Since bilinear texture interpolation already provides

a C

-continuous ﬁlter even without the overhead of

a pyramid method, the equivalent synthesis ﬁlter is

not very useful in itself; however, it may be used as a

building block for more complex synthesis ﬁlters. It is

called h

midpoint

because of the corresponding midpoint

subdivision scheme; its deﬁnition is:

1,1

midpoint

def





0 0 0

0 1 1





1,0

midpoint

def





0 0 0

0 1 0





0,1

midpoint

def



1,0

midpoint



⊤

0,0

midpoint

def

= h

0,0

nearest

Note that h

0,0

midpoint

corresponds to the convolution

ﬁlter for sampling positions at pixel centers while

1,1

midpoint

corresponds to the convolution ﬁlter for sam-

pling positions at their corners, and the remaining two

ﬁlters correspond to the centers of edges of pixels.

Also note that the ﬁrst row and the ﬁrst column of

the new image data will be sampled at the upper, left

corners of “old” pixels and the midpoints of edges be-

tween these positions. Therefore, the presented con-

volution ﬁlters will access “old” pixels of the 0-th row

and 0-th column. In practice, these lookups could re-

turn the corresponding pixel data of the ﬁrst row and

ﬁrst column, respectively. An alternative is to discard

the ﬁrst row and ﬁrst column of the resulting image.

5.3 C

-Continuous Filter

The synthesis ﬁlter discussed here corresponds to

the biquadratic B-spline subdivision scheme (Catmull

and Clark, 1978), also known as the Doo-Sabin sub-

division scheme for regular quadrilaterals or the two-

dimensional generalization of the Chaikin scheme. It

is an approximating vertex-split subdivision scheme;

thus, all pixels are processed in symmetric ways:

1,1

Doo-Sabin

def





0 0 0

0 9 3

0 3 1





1,0

Doo-Sabin

def





0 0 0

3 9 0

1 3 0





0,1

Doo-Sabin

def



1,0

Doo-Sabin



⊤

0,0

Doo-Sabin

def





1 3 0

3 9 0

0 0 0





The implementation of this synthesis ﬁlter

requires only one bilinear texture interpolation

(Strengert et al., 2006). Note that the convolution

for all boundary pixels of the resulting image accesses

pixels outside of the original image.

Our notation also suggests an equivalent but less

efﬁcient implementation variant with two texture in-

terpolations instead of one:

Doo-Sabin

⊗

↑

g ≡ h

box

⊗



midpoint

⊗

↑



Another synthesis ﬁlter may be constructed by re-

ordering the convolution ﬁlters:

midpoint

⊗

↑



box

⊗ g



PYRAMID FILTERS BASED ON BILINEAR INTERPOLATION

Since the resulting synthesis ﬁlter is only C

continuous and requires one additional texture inter-

polation, there is no apparent advantage compared to

the C

-continuous h

Doo-Sabin

ﬁlter.

5.4 C

-Continuous Filter

The C

-continuous synthesis ﬁlter corresponding to

the bicubic B-spline subdivision scheme can be con-

structed easily in our notation with the help of one

additional convolution with a 2× 2 box ﬁlter:

cubic

⊗

↑

g ≡ h

box

⊗



Doo-Sabin

⊗

↑



Permutations of the components of this construc-

tion result in less symmetric and/or less smooth syn-

thesis ﬁlters. On the other hand, the construction of

higher-order B-spline ﬁlters by additional convolu-

tions with 2 × 2 box ﬁlters should now be obvious.

Note, however, that h

box

and h

box

should appear in al-

ternating order as discussed in Section 3.

5.5 (Quasi-)Interpolating Filters

Unfortunately, the construction of aC

-continuous in-

terpolation synthesis ﬁlter is considerably more dif-

ﬁcult than the approximation synthesis ﬁlter corre-

sponding to B-splines. If quasi-interpolation is sufﬁ-

cient, the image data of the coarsest level can be con-

volved with a ﬁlter before the synthesis is performed.

The computation of appropriate convolution ﬁlters is

discussed by Litke et al. (Litke et al., 2001). For

example, a convolution ﬁlter for quasi-interpolation

with bicubic B-splines can be constructed that is im-

plementable with three texture interpolations:





−1 −2 −1

−2 36 −2

−1 −2 −1





≡





0 0 0





−

3×3

Bartlett

Our recommendation for an actually interpolat-

ing, C

-continuous synthesis ﬁlter corresponds to the

tensor-product generalization of the four-point sub-

division scheme. Since it is separable by construc-

tion, it can be implemented by a synthesis operation

for the rows followed by a synthesis operation for the

columns. This appears to result in the most efﬁcient

implementation using 4.5 bilinear texture interpola-

tions per pixel of the resulting image.

6 CONCLUSION

In this work, a set of discrete pyramid ﬁlters that are

suitable for an efﬁcient implementation based on bi-

linear texture interpolation has been presented. A

new, precise and consistent notation for convolutions

with these ﬁlters enabled us to construct appropriate

ﬁlters in a systematic way and helped us to discuss

many important implementation details. In particular,

we have proposed an efﬁcient implementation of bi-

quadratic (and higher-order) B-spline analysis ﬁlters

and of bicubic (and higher-order) B-spline synthesis

ﬁlters.

Apart from applications of these ﬁlters, our plans

for future work on pyramid ﬁlters include more efﬁ-

cient interpolating synthesis ﬁlters, three-dimensional

ﬁlters, and efﬁcient implementations of derivative ﬁl-

ters and nonlinear ﬁlters.

REFERENCES

Burt, P. J. (1981). Fast Filter Transforms for Image Pro-

cessing. Computer Graphics and Image Processing,

16:20–51.

Catmull, E. and Clark, J. (1978). Recursively Generated

B-Spline Surfaces on Arbitrary Topological Meshes.

Computer Aided Design, 10(6):350–355.

Green, S. (2005). Image Processing Tricks in OpenGL. Pre-

sentation at GDC 2005.

uger, J. and Westermann, R. (2003). Linear Algebra Op-

erators for GPU Implementation of Numerical Algo-

rithms. ACM Transactions on Graphics, 22(3):908–

916.

Lefebvre, S., Hornus, S., and Neyret, F. (2005). Octree Tex-

tures on the GPU. In Pharr, M., editor, GPU Gems 2,

pages 595–613. Addison Wesley.

Litke, N., Levin, A., and Schroeder, P. (2001). Fitting Sub-

division Surfaces. In Proceedings IEEE Visualization

2001, pages 319–324.

Sigg, C. and Hadwiger, M. (2005). Fast Third-Order Tex-

ture Filtering. In Pharr, M., editor, GPU Gems 2,

pages 313–329. Addison Wesley.

Strengert, M., Kraus, M., and Ertl, T. (2006). Pyramid

Methods in GPU-Based Image Processing. In Pro-

ceedings Vision, Modeling, and Visualization 2006,

pages 169–176.

Williams, L. (1983). Pyramidal Parametrics. In Proceed-

ings ACM SIGGRAPH ’83, pages 1–11.

Zorin, D., Schr

oder, P., DeRose, T., Kobbelt, L., Levin, A.,

and Sweldens, W. (2000). Subdivision for Modeling

and Animation. SIGGRAPH 2000 Course Notes.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications