BUILDING 3D INDOOR SCENES TOPOLOGY FROM

2D ARCHITECTURAL PLANS

Sebastien Horna, Guillaume Damiand, Daniel Meneveaux and Yves Bertrand

SIC laboratory, University of Poitiers, France

Keywords:

3D modelling, architectural scenes, reconstruction, topological model.

Abstract:

This paper presents a new method for reconstructing geometry and topology of 3D buildings from 2D ar-

chitectural plans. A complete topological model expresses incidence and adjacency relations between all the

elements. It is necessary for both recovering accurately 2D information and constructing a coherent 3D build-

ing. Based on an existing topological kernel, several high-level operations have been developped in 2D for

creating walls, portals, stairs, etc. Semantic information is associated with all volumes for specifying open-

ings, walls, rooms, stairs, facade, etc. The resulting 2D model is extruded for generating a 3D environment,

taking the semantic information into account since doors are not processed as walls for instance. Floors are

superimposed using volumes corresponding to upper and lower ceilings linked according to stairways. The

resulting models are suitable for various application such as walkthrough, lighting/wave propoagation/thermal

simulation.

1 INTRODUCTION

Accurate three dimensional descriptions of architec-

tural environments is an important need for many

building trades such as lighting engineering, thermal

simulations, etc. Generally, the models produced by

the architects are handled in two dimensions with-

out any topological information. However, in addi-

tion to a three dimensional description of the model,

many simulation algorithms require adjacency and in-

cidence relationships between volumes.

Unfortunately, manually reconstructing complex

architectural scenes using a 3D modeller is a long

and tedious process. This is why we propose a new

method for automatically reconstructing 3D buildings

from 2D architectural plans (ﬁgure 1). Our method in-

herently integrates a complete topological description

of the environment. The resulting scenes can thus be

edited in a topological modeller for adding furniture,

moving walls, etc. In addition, semantic information

is used for deﬁning object attributes such as rooms,

ﬂoor, corridors and so on.

Our aim is to deﬁne a building model correspond-

ing to a 3D partition of space. Each room should cor-

Figure 1: 2D plan and 3D reconstruction.

respond to a closed and orientable volume, incident

to closed and orientable faces. Amongst the existing

topological models, we have chosen generalized maps

which allow to represent space subdivisions and inci-

dence and adjacency relations.

The reconstruction method we propose is based

on four main phases: (i) 2D edges processing for

removing geometrical inconsistencies, (ii) topologi-

cal reconstruction with semantic information, (iii) 3D

building extrusion (iv) superimposing of ﬂoors. Dur-

ing the ﬁrst phase, most 2D imprecisions (90%) are

automatically corrected. However, remaining awk-

ward elements can be semi-automatically processed.

Semantic information can be deduced from the plans

Horna S., Damiand G., Meneveaux D. and Bertrand Y. (2007).

BUILDING 3D INDOOR SCENES TOPOLOGY FROM 2D ARCHITECTURAL PLANS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 37-44

DOI: 10.5220/0002076700370044

 SciTePress

when they exist, or deﬁned manually by the user. The

extrusion operation is guided by the semantics. For

instance, walls, doors or stairs are extruded using spe-

ciﬁc rules. Superimposing of ﬂoors is applied using

semantics and topology.

The resulting topological indoor models have

been designed so that volumes adjacency can be ef-

ﬁciently used for various types of simulation. For in-

stance such models prove efﬁcient in the context of

radiosity or photon mapping approaches (Meneveaux

et al., 1998a; Fradin et al., 2005).

This paper is organized as follows. Section 2

describes the existing methods for 3D architectural

scenes construction. Section 3 justiﬁes our choice of

generalized maps. Section 4 presents our method of

geometrical and topological rebuilding in two dimen-

sions. Section 5 details the extrusion and superimpos-

ing of several ﬂoors. Section 6 discusses the results

obtained with several examples of real buildings.

2 RELATED WORK

Many methods in the literature propose to rebuild ur-

ban environments. For instance, the MATIS team

in the research section of the French Institut Ge-

ographique National (IGN) proposes an elevation

method starting from satellite photographs (Fuchs

et al., 2003). Ah-Soon et al. processes digitized 2D

drawings (i.e. images of plans) for 3D reconstruc-

tion (Ah-Soon, 1998). Recognition is based on the

detection of vertical and horizontal symbols. The

aim is to analyze the interior geometry of a build-

ing as well as the openings location (doors, windows,

etc). This work primarily concerns methods of image

analysis. The geometry reconstruction produces 3D

scenes without topological information.

Several methods aim at extracting topological in-

formation from a list of polygons, making it possi-

ble to reduce calculations of visibility for lighting

simulation and visualization. Airey et al. propose

a method of binary space subdivision (Binary Space

Partitioning or BSP) for axis-aligned environments

(Airey et al., 1990). Teller et al. present an extension

of this method for all types of walls (Teller, 1992).

Meneveaux et al. propose a method containing rules

to ﬁnd the parts of the buildings (Meneveaux et al.,

1998b). All these subdivision schemes produce a set

of regions called cells, separated by openings. The

topological description corresponds to adjacency rela-

tions between 3D cells, there no incidence/adjacency

relations between lower-dimensions elements.

Complex urban scenes can also be produced us-

ing procedural modeling, such as cityEngine (Parish

and Muller, 2001; Muller et al., 2006). Several pa-

rameters can be taken into account: population den-

sity or height maps. The road network is generated

using a L-System mechanism. A construction gram-

mar is used to create the building facade. Although

these methods generate realistic (but not real) geo-

metrical environments, topological information is not

managed.

3 GENERALIZED MAPS

We wish to represent buildings made up of volumes

(ﬂoors, walls, rooms, etc), each of them being a ori-

entable 3D object. We need a subdivision of space

into faces, edges, vertices, deﬁned by their boundaries

(boundary representation) in any dimension. Maps

and generalized maps offer an implicit representation

of cells with efﬁcient operations since a local modiﬁ-

cation in the map is automatically propagated to the

incident edges.

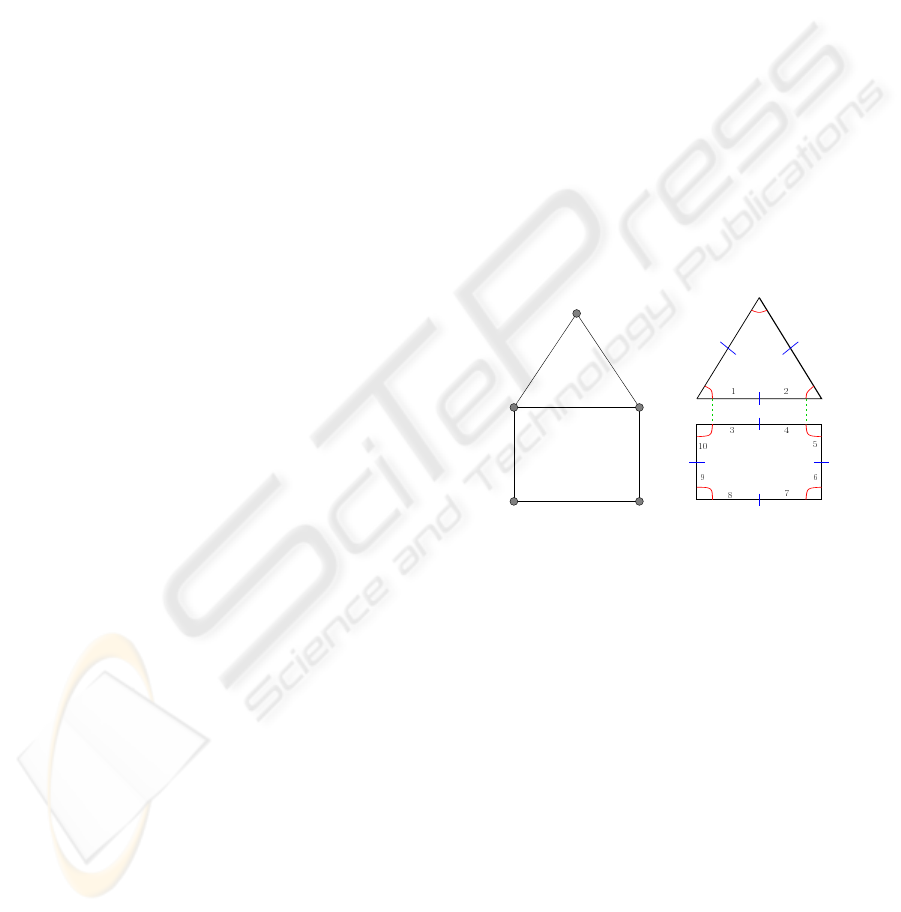
(a) (b)

Figure 2: (a) A 2D object containing 2 faces, 6 edges

and 5 vertices; (b) corresponding generalized map: the

set of darts {1,2,3,4} represents an edge, the set of darts

{3,4,5,6,7,8,9,10} represents a face.

Several topological models allowing space subdi-

visions have been proposed in the literature: struc-

tures containing adjacency graphs (Brisson, 1993),

2D/3D models based on edges (Baumgart, 1975;

Guibas and Stolﬁ, 1985; Weiler, 1986) or models ca-

pable of handling higher dimensions (Brisson, 1993;

Lienhardt, 1994). As explained in the following sec-

tion, many reasons have motivated our choice for gen-

eralized maps (Lienhardt, 1994).

It has been shown in (Lienhardt, 1991) that exist-

ing topological models representing 3D subdivisions

are comparable with 3D maps (for orientable models

without boundary) or with 3D generalized maps (for

orientable or not models, with or without boundary).

Even though 3D generalized maps are more expen-

sive than 3D maps in the memory, we have chosen

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

this model since it provides a homogeneous represen-

tation in all dimensions. This simpliﬁes many opera-

tion deﬁnitions.

From a single type of basic elements (called darts)

and one to one mappings α deﬁned on these darts,

generalized maps represent object cells and adja-

cency/incidence relationships. Each mapping α

, with

0 ≤ i ≤ n (n being the highest dimension used), rep-

resents the adjacency relations between i-dimensional

cells;

Deﬁnition 1 (Generalized map (Lienhardt, 1994))

A generalized map in dimension n ≥ 0 (or n-G-map)

is an algebra G = (D, α

, ..., α

), where:

- D is a ﬁnite set of darts;

- α

, ..., α

are involutions

;

- α

an involution for all i, j such that

0 ≤ i < i+ 2 ≤ j ≤ n.

Two darts d and d

′

are α

-sewed if dα

= d

′

with

d 6= d

′

, and d is α

-free if dα

= d. The i-cell asso-

ciated with a given dart d is composed of all the darts

obtained by a coverage starting from d and using all

the involutions except α

(see ﬁgure 2). The number

of distinct edges incident to a vertex deﬁnes its de-

gree. When the vertex is incident to only one edge,

the edge is called a dangling edge.

On the basis of this representation, we have

used the 3D topological modeller MOKA (Vidil and

Damiand, 2003), comprising many operations such as

sewing two cells along a face or more complex oper-

ations like sweeping or coreﬁning.

4 2D RECONSTRUCTION

For extruding a 3D building, a valid topology has to

be reconstructed from the 2D plan. Therefore, the

dataset has to comply with three fundamental proper-

ties: (i) edges should not be merged, (ii) edges should

not intersect (iii) edge vertices should all be incident

to another edge. (i) and (ii) ensure that the plan is a

partition of a 2D space in faces, edges and vertices. In

a 2D architectural plan every object is usually deﬁned

with a given thickness. Consequently edges should

not be isolated, which corresponds to (iii). When

these 3 properties are veriﬁed, the set of edges is said

valid.

A bijection f is an involution iff f

= Id

If β and γ are applications of E → E, βγ corresponds

to the composition γ ◦ β, and bβγ is the application of this

composition to element b of E.

Unfortunately, modeller software used by archi-

tects is not devised for 3D topological extrusion. Con-

sequently, in most cases, none of the above proper-

ties is maintained. The reconstruction robustness of

our method highly depends on the detection and cor-

rection of all geometrical inconsistencies contained

in the 2D plans. Our application corrects geometry

and builds up the topological model. It is composed

of two parts: the ﬁrst one consists of geometry error

detection and correction while the second one con-

structs topological information. The ﬁnal goal is to

link edges so as to produce 2D faces.

In practice, for the plans we have used, 90% of

imprecisions are automatically corrected. However,

some remaining awkward elements have to be pro-

cessed. Therefore, we propose semi-automatic opera-

tions for correcting the plans (see section 4.4).

Semantic information can be deduced from the

plans when it exists, or deﬁned manually by the user.

Finally, each type of object contained in plans is asso-

ciated with semantics: walls, rooms, openings, stairs,

etc.

The general algorithm of 2D reconstruction is bro-

ken up into the following steps: (1) edge extraction

from source ﬁle (2) geometry correction (3) topolog-

ical construction (4) semi-automatic ﬁnalization (5)

semantics association.

4.1 Geometrical Correction

Once the edges have been identiﬁed in the source ﬁle,

the plan analysis is performed. Therefore, a threshold

ε is deﬁned for testing whether two edges are super-

imposed and ﬁnding all the edges incident to a given

vertex. In practice, we have ﬁxed ε = 1mm.

Two edges are superimposed if they have the same

slope, the same origin ordinate and at least one ex-

tremity included in the other edge. In this case, both

edges are merged into a single one.

All the edge intersections are processed two by

two. If an intersection is found, a vertex is added at

the intersection point on the concerned edges.

4.2 Topological Reconstruction

The above processing produces a set of valid seg-

ments used to construct topology. All the adjacency

and incidence relationships between vertices, edges

and faces have to be deﬁned.

4.2.1 Edges Creation

Each edge is associated with four darts corresponding

in 2D to an edge shared by two faces. Links α

and α

BUILDING 3D INDOOR SCENES TOPOLOGY FROM 2D ARCHITECTURAL PLANS

are immediately set on the corresponding darts. Only

remain to be processed for creating faces.

Since buildings are orientable objects, composed

of orientable elements, we also need to set an ori-

entation to the whole generalized map. This is why

darts are associated with a boolean mark indicating

the edge orientation. For a dart d marked, dα

, dα

and dα

are not marked.

4.2.2 Angle Arrangement

For 1 and 2-degrees vertices, the corresponding darts

are directly connected by α

. For each vertex of

higher degree, the incident edges are stored and sorted

according to their angle around the vertex. The algo-

rithm is the following:

1. search for dart d α

-free;

2. search for all darts {d

} α

-free, incident to d;

3. sort {d

} according to the angle with d (corre-

sponding to the angle formed by the associated

edges);

4. α

-sew the darts two by two according to this or-

der, with respect to the orientation constraints.

4.2.3 Face Inclusion

In most plans, some objects are included in others.

For instance, stairs are included in rooms. Unfortu-

nately, with boundary representations, these objects

are not connected. Consequently, there is no rela-

tive position between elements. This is why we have

used ﬁctive edges for linking the existing connected

components. On the ﬂoor, a ﬁctive edge is thus used

to link an external face to the included ones. These

edges are called ﬁctive edges since they do not repre-

sent the boundary of a face.

4.3 Accelerating Structure

With the process described above, many operations

require testing couples of darts according to their lo-

cation in the plans. The use of an accelerating struc-

ture makes it possible to reduce the processing time.

Since the plans scale is deﬁned in meters, we choose a

uniform grid made up of 1meter× 1meter tiles. Each

tile is associated with the list of segments which cross

it. Thus, for each segment, tests are performed only

in a local neighborhood. Note that segments corre-

sponding to walls only belong to a few tiles.

4.4 Additional Operations

To eliminate inconsistencies that are not auto-

matically corrected, we propose several semi-

automatically operations. Based on the low-level op-

erations sew and removal deﬁned in (Damiand and

Lienhardt, 2003), we propose higher-level operations

for processing several edges at the same time: (i) for

sewing two selected edges; (ii) for sewing several se-

lected dangling edges to the closest edge; (iii) for

sewing all the dangling edges to the closest edge; (iv)

for topologically removing n selected edges.

It can be necessary to add doors on the plans. We

also propose an operation for creating a door, starting

from the selection of two walls. A door is inserted in

the plan, and associated with its semantic.

4.5 Semantic Deﬁnition

Semantic information allows the user to know the

type of each element in the plan. The objects are clas-

siﬁed into various categories: walls, doors, ﬂoor, ceil-

ing, stairs, etc. Any type of new information can be

conveniently added to the model. In practice, each

dart holds a label corresponding to its semantic.

During the reconstruction process, it is possible to

use the layers contained in the source ﬁle for indicat-

ing the semantic of objects. The user can also select

part(s) of the building and manually modify seman-

tics. This information is used for guiding the extru-

sion process described below.

5 3D EXTENSION

The starting point of the 3D extrusion is a 2D plan

composed of faces, edges and vertices associated with

a consistent topology (i.e. an orientable 2D partition,

closed and without dangling edges). Each ﬂoor is

handled using several types of operations. Therefore,

we have adapted the extrusion already existing in the

MOKA library. Each type of element is speciﬁcally

processed.

The topological 3D representation has to comply

with several important features.

1. The 3D model must be a closed space since each

room, wall and portal are deﬁned as a closed vol-

umes. For instance, rooms are deﬁned by volumes

with transparent faces corresponding to portals.

Consequently, each face should be incident to ex-

actly two volumes. Obviously, faces also have to

be closed as well as edges.

2. Each building must be composed of a single 3D

connected component. For instance, faces or vol-

umes deﬁning holes have to be connected with

their respective faces or volumes.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

3. The model must be oriented since each part of the

building should be clearly identiﬁed as the inside

or the outside.

These constraints are guaranteed by the properties

of the 2D plan and the extrusion operation.

Finally, the building extrusion is organized as fol-

lows: (i) extrusion of the ﬂoor (wall, doors), (ii) cre-

ation of the ground and ceiling, (iii) superposition of

ﬂoors, (iv) stairs construction.

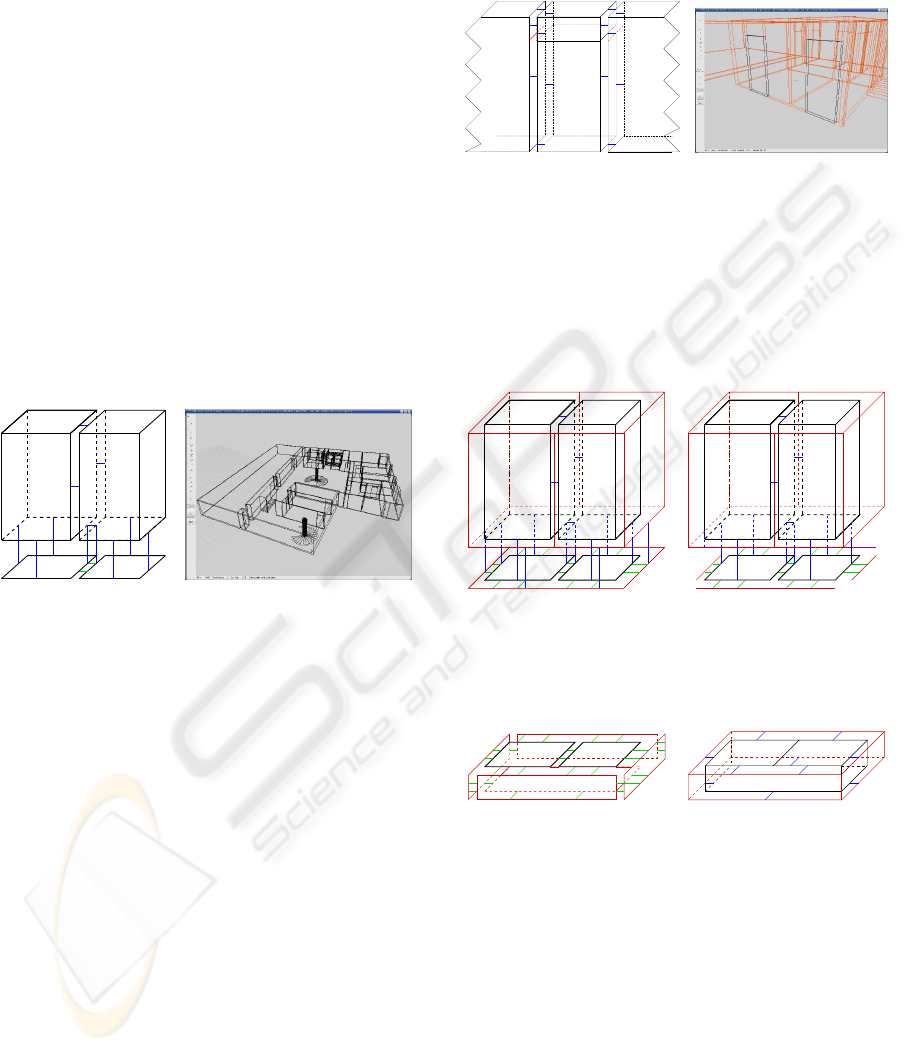
5.1 Extrusion of Walls

For extruding walls, a vertical path is deﬁned with a

height equal to 2, 5 meters. From each face of the

2D plan, a volume is automatically created and con-

nected using α

to the corresponding face (see ﬁgure

3). Contrary to existing modeler, our topological ex-

trusion of two faces connected by α

produces two

volumes connected by α

. Note that ﬁctive edges are

not extruded so that no useless ﬁctive face be created.

V1 V2

F1 F2

(a) (b)

Figure 3: Extrusion of walls: (a) volumesV

andV

are built

and connected to the corresponding faces F

and F

. Since

and F

are connected by α

, V

and V

are connected by

. (b) sample ﬂoor with walls extrusion.

The extrusion operation deﬁned above allows the

construction of non vertical walls (the extusion path

has to be properly deﬁned). However, in most cases

the slope is not deﬁned on the plans. Moreover, the

modeler MOKA can be easily used for modifying the

upper wall edges.

5.2 Extrusion of Opennings

On the plans, door volumes are topologically con-

nected to the surrounding walls. The portion of wall

above to the door is created. Therefore, the 2D poly-

gon representing the door is extruded according to a

vertical path of two components (corresponding to the

opening and the portion of wall above the door). The

two resulting volumes are superimposed and topolog-

ically connected. In a second step, they are connected

to the remainder of the building, along the door stiles.

Two vertices and an edge must be inserted on the

stiles to respect the topological constraints (ﬁgure 4).

For windows, the same operation can be applied

with an additionnal component corresponding to the

wall part located under the window.

DOOR

(a) (b)

Figure 4: Door extrusion: (a) extrusion and connexion to

the walls W

and W

, the section of wall named W

is built

above the door. Four vertices (V

) and two edges,

and A

, are inserted on M

and M

. (b) Result of door

extrusion.

5.3 Creation of Grounds and Ceilings

V1 V2

F1 F2

(a)

V1 V2

F1 F2

(b)

Figure 5: (a) Contour faces are marked for being used dur-

ing the creation of the ﬂoor; (b) α

and α

are unsewed for

the 2D plan contour.

F1 F2

(a)

F1 F2

(b)

Figure 6: Ground creation: (a) the 2D plan contour is used

to construct the ground volume; (b) the ground volume is

closed (red volume corresponding to the outer part).

With the extrusion system described above, the

darts of the 2D plan are α

-connected to volumes

deﬁning walls or doors (ﬁgure 5.a).

The 2D plan is used to create the ground volume

(ﬂagstone). Therefore, the contour of the 2D plan

is α

and α

-disconnected (ﬁgure 5.b) and the corre-

sponding edges are used to form the desired volume

(Figure 6). The external faces of this volume are α

sewed with the faces representing the ﬂoor contour

(ﬁgure 7).

BUILDING 3D INDOOR SCENES TOPOLOGY FROM 2D ARCHITECTURAL PLANS

F1 F2

(a)

F1 F2

(b)

Figure 7: (a) The outer ground volume is sewed by α

to the

extern ﬂoor volume (facade); (b) the resulting open volume

(in red) represents the ﬂoor facade and the ground.

F1 F2

F’1 F’2

(a)

F1 F2

(b)

Figure 8: Ceilings creation: (a) the horizontal faces at the

top of the ﬂoor are duplicated; (b) duplicated faces are used

for creating the ceiling volume with the same method as for

grounds. The resulting closed volume describes the facade

and actually deﬁnes the rest-of-the-world volume.

The construction of the ceiling requires the copy

of the 2D plan at the top of the ﬂoor (Figure 8.a). Dur-

ing duplication, each new dart is sewed by α

to its

corresponding dart. The external segment is used to

construct the ceiling volume (Figure 8.b). The exter-

nal faces are sewed by α

with the darts of the 3D

ﬂoor contour. This operation produces 4 types of vol-

umes: ground, ceiling, indoor description, facade.

5.4 Superimposing of Floors

For superimposing two ﬂoors with same outer 2D

shape, the ground of the upper ﬂoor is connected to

the ceiling of the lower ﬂoor (Figure 9). In practice,

the two volumes are sewed by α

and the shared face

is removed. Thus, only one volume deﬁnes the space

between the two ﬂoors.

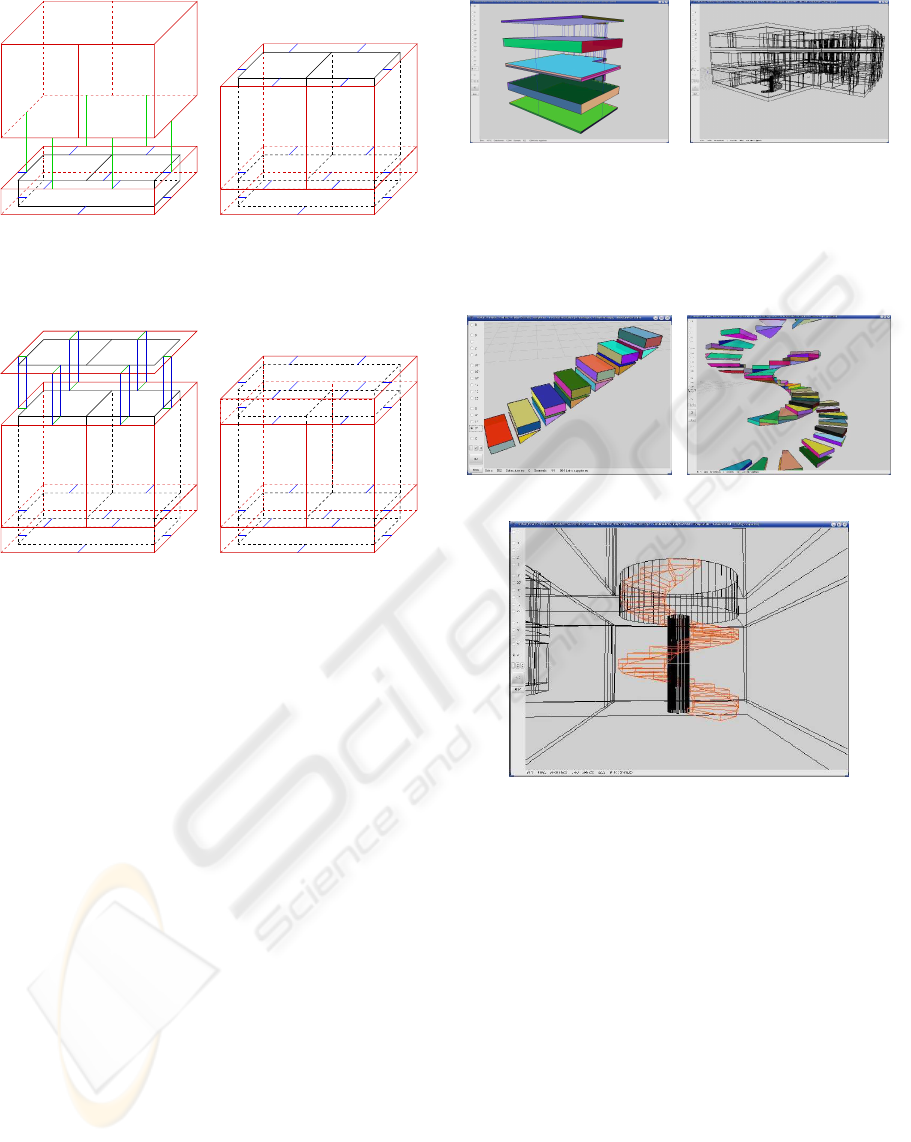
5.5 Creation of Stairs

Stairs can be deﬁned with various shapes on the 2D

plans: straight, snail, elliptic, etc. They are often

(a) (b)

Figure 9: Creation of grounds and ceilings. (a) Visualiza-

tion of the connections between the grounds and ceilings of

two ﬂoors. The ceiling of the lower ﬂoor and the ground of

the upper ﬂoor are merged. (b) Building made up of two

superimposed ﬂoors.

(a) (b)

(c)

Figure 10: Construction of stairs. (a) Steps of a straight

staircase composed of two volumes. (b) Volumes deﬁning

snail stairs. (c) Result of snail stairs in a building with ceil-

ing opening.

disconnected from the rest of the plan or joined to

the walls. We propose a generic method for creat-

ing the stairs topology. The steps geometry is com-

puted according to the data recovered on the plan

(length, width, or diameter in the case of spiral stairs).

Presently, our method does not provide any automatic

system for detecting the geometric type of stairs, the

user manually selects the appropriate method.

Each step is composed of two volumes (ﬁgure

10.a). A surrounding volume ensures the model

closeness (ﬁgure 10.b). Once created, the 3D stair

is connected to the remainder of the plan by a ﬁc-

tive edge. The ceiling is perforated according to the

stair shape using of a boolean operation. Therefore

the stair contour is extruded according to the ceiling

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

Figure 11: Result of 3D stair reconstruction.

height and the resulting volume is subtracted from the

ceiling so as to create the opening (Figure 11).

6 IMPLEMENTATION AND

RESULTS

Our reconstruction system has been implemented in

C++, using the MOKA library (Vidil and Damiand,

2003). The source ﬁles have been produced by ar-

chitects in dxf format. Computing times have been

obtained with a centrino processor: 2Ghz and 1GB of

RAM.

We have applied our reconstruction method to var-

ious 2D architectural plans. The processing times for

the 2D analysis are presented Table 1. They depend

on the distribution of the segments in the plan and

on the uniform grid acceleration. The processing of

a ﬂoor never exceeds one minute, even for complex

plans.

(a) plan 1 (b) plan 2

Figure 12: Plans used for geometrical and topological re-

construction.

Table 1: Processing time of the automatic 2D reconstruc-

tion.

Buildings # Segments Geometric Topological

of the scene processing processing

plan 1 899 2s 1s

plan 2 8050 9s 16s

plan 3 8120 11s 13s

plan 4 11972 56s 59s

Figure 13: Result of reconstruction 3D.

With the proposed method, 90% of the plans inco-

herencies have been detected and corrected automat-

ically. The time required for manually correcting the

2D models incoherencies is about a few hours, de-

pending on the model complexity and the numbers

of errors contained in the plan. From this point, the

3D reconstruction becomes completely automatic and

takes only a few seconds. Moreover, all the topo-

logical and semantical information are automatically

propagated.

7 CONCLUSION

This paper presents a new method for reconstructing

a 3D description of buildings from 2D architectural

plans. The resulting description includes geometry

and topology so that the whole environment consis-

tency be preserved according to constraints such as

closeness, orientability, and connectivity.

The main steps of our method concern: (i) a geo-

metrical correction of source data, (ii) a 2D topology

construction, (iii) a 3D extrusion system, (iv) ﬂoors

superimposing. We also propose semi-automatic

tools for correcting 2D plans. The results obtained

show that 2D and 3D processing require only a few

tens of seconds.

The main advantage of our method concerns the

use of topology for validating the building structure

coherence and editing the model using modelling op-

BUILDING 3D INDOOR SCENES TOPOLOGY FROM 2D ARCHITECTURAL PLANS

erations. Furthermore, the resulting structure pro-

vides various types of information necessary for vi-

sualization or lighting/thermal/low-frequency wave

propagation simulations (Meneveaux et al., 1998a;

Fradin et al., 2005; Teller et al., 1994).

The next step of this work consists in automat-

ically deﬁning additional semantics (such as rooms

or furniture for instance). Thus operations dedicated

to volume types can be explored for simplifying the

3D models. We also aim at automatically detecting

stairs and their characteristics. Moreover, additional

operations have to be deﬁned, for instance related to

windows, roofs or superimposed ﬂoor with different

shapes.

In the future, we wish to apply our system to ur-

ban scenes as well, containing furnished buildings,

etc. This implies the processing of larger data with

missing information. We aim at coupling our system

with procedural reconstruction methods.

REFERENCES

Ah-Soon, C. (1998). Analyse de Plans Architecturaux. Phd

thesis, INPL.

Airey, J. M., Rohlf, J. H., and F. P. Brooks, J. (1990). To-

wards image realism with interactive update rates in

complex virtual building environments. In ACM Sym-

posium on Interactive 3D Graphics, pages 41–50.

Baumgart, B. (1975). A polyhedron representation for com-

puter vision. In AFIPS Nat. Conf. Proc. 44, pages

589–596.

Brisson, E. (1993). Representing geometric structures in d

dimensions : topology and order. Discrete & Compu-

tational Geometry, 9:387–426.

Damiand, G. and Lienhardt, P. (2003). Removal and con-

traction for n-dimensional generalized maps. In Dis-

crete Geometry for Computer Imagery, number 2886

in Lecture Notes in Computer Science, pages 408–

419, Naples, Italy.

Fradin, D., Meneveaux, D., and Horna, S. (2005). Out-of-

core photon-mapping for large buildings. Eurograph-

ics Symposium on Rendering EGSR 2005, Konstanz,

Germany.

Fuchs, F., Jibrini, H., Maillet, G., Paparoditis, N., Deseil-

ligny, M., and Tailandier, F. (2003). Trois approches

pour la reconstruction automatique de modle 3-d de

btiments en imagerie arienne haute rsolution. Bulletin

d’information de l’IGN n73 (2002/2003), pages 17–

26.

Guibas, L. and Stolﬁ, J. (1985). Primitives for the ma-

nipulation of general subdivisions and the computa-

tion of voronoi diagrams. Transactions on Graphics,

4(2):131–139.

Lienhardt, P. (1991). Topological models for boundary rep-

resentation: a comparison with n-dimensional gener-

alized maps. Computer-Aided Design, 23(1):59–82.

Lienhardt, P. (1994). N-dimensional generalized combi-

natorial maps and cellular quasi-manifolds. Interna-

tional Journal of Computational Geometry & Appli-

cations, 4(3):275–324.

Meneveaux, D., Bouatouch, K., and Maisel, E. (1998a).

Memory management schemes for radiosity computa-

tion in complex enviroments. In Computer Graphics

International.

Meneveaux, D., Bouatouch, K., Maisel, E., and Delmont, R.

(1998b). A new partitioning method for architectural

environments. Journal of Visualization and Computer

Animation, 9(4):195–213.

Muller, P., Wonka, P., Haegler, S., Ulmer, A., and Gool,

L. V. (2006). Procedural modeling of buildings. ACM

Trans. Graph., 25(3):614–623.

Parish, Y. I. H. and Muller, P. (2001). Procedural modeling

of cities. Computer Graphics (ACM SIGGRAPH’01

Proceedings).

Teller, S. (1992). Computing the antipenumbra of an

area light source. In Computer Graphics (ACM SIG-

GRAPH’92 Proceedings).

Teller, S., Fowler, C., Funkhouser, T., and Hanrahan, P.

(1994). Partitioning and ordering large radiosity

computations. In Computer Graphics (ACM SIG-

GRAPH’94 Proceedings), pages 443–450.

Vidil, F. and Damiand, G. (2003). Moka.

www.sic.sp2mi.univ-poitiers.fr/moka/.

Weiler, K. (1986). The radial-edge data structure: a

topological representation for non-manifold geometry

boundary modeling. In Proc. IFIP WG 5.2 Working

Conference, Rensselaerville, USA.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications