HIERARCHIC MODELING OF SYMMETRIC GEOMETRIES

Pritee Khanna, Puneet Tandon

PDPM-Indian Institute of Information Technology, Design & Manufacturing Jabalpur, India

Sanjay G. Dhande

Director, Indian Institute of Technology Kanpur, India

Keywords: Geometric Modeling, Motifs, Patterns, Layouts, Symmetry.

Abstract: The world is full of procedural ornaments, especially in cultural heritage. These ornaments are often said to

be too complex for automatic modeling, and too tedious for manual modeling. A pattern is an orderly

arrangement of objects in space. In this work, a geometric model for symmetric patterns is proposed. The

two-dimensional hierarchic model represents pattern as a tree. The model when implemented reads in a

motif description, builds a tree of motifs and renders the pattern as well as final layout. Interactive editing of

motif descriptions can be performed with a GUI.

1 INTRODUCTION

All natural and man-made things have an order built

inside them. Abstract things like language and music

also have some inherent order that provides a

pleasant feeling to our senses. Patterns in nature are

formed by biological systems or by inanimate things

(Tarasov, 1986). Manmade patterns are usually

simplified version of natural patterns, copied

knowingly or unknowingly by artists, and passed on

as a tradition from one generation to the next.

Patterns are visible in art, architecture, and items of

daily use such as textiles, utensils, furniture and

decorative objects.

CAD tools allow designers to manipulate a set of

fundamental blocks and to arrange the blocks into

some definite order to form a pattern. These tools

are not a substitute for artistic skills. The user of

such tools needs to have some kind of artistic talent

to utilize them efficiently and produce pleasing

designs. If we could have a tool that has “artistic

sense” built into it, then it would be possible for a

non-artist person to design and experiment with

patterns. Such sense can be put into a computer tool

if we can encode the design in a format that is

understood by a computer as something more than

just a bunch of shapes put together.

Tarasov (Tarasov, 1986) describes different

kinds of symmetry and applications of symmetry as

an engine in different walks of life. Glassner

(Glassner, 2000) has generated textures using the

concept of symmetry. Cohen et al. (Cohen et al.,

2003) have generated images and textures through

wang tiles. Various examples of jigsaw image

mosaics, crop art and border patterns are illustrated

in (Kim & Pellacini, 2002), (Glassner 2004) and

(Wolfe, 1996) respectively.

The present work is geared towards design of

patterns that are used in textiles, perhaps more

prominent in embroidered works. Such patterns are

usually floral patterns, displaying dynamic

symmetry. This paper proposes a hierarchical

computable model for such patterns that makes

abundant use of primitive instancing. Primitive

instancing allows us to reuse the same primitive at

multiple locations in the pattern without duplicating

the description of the motif.

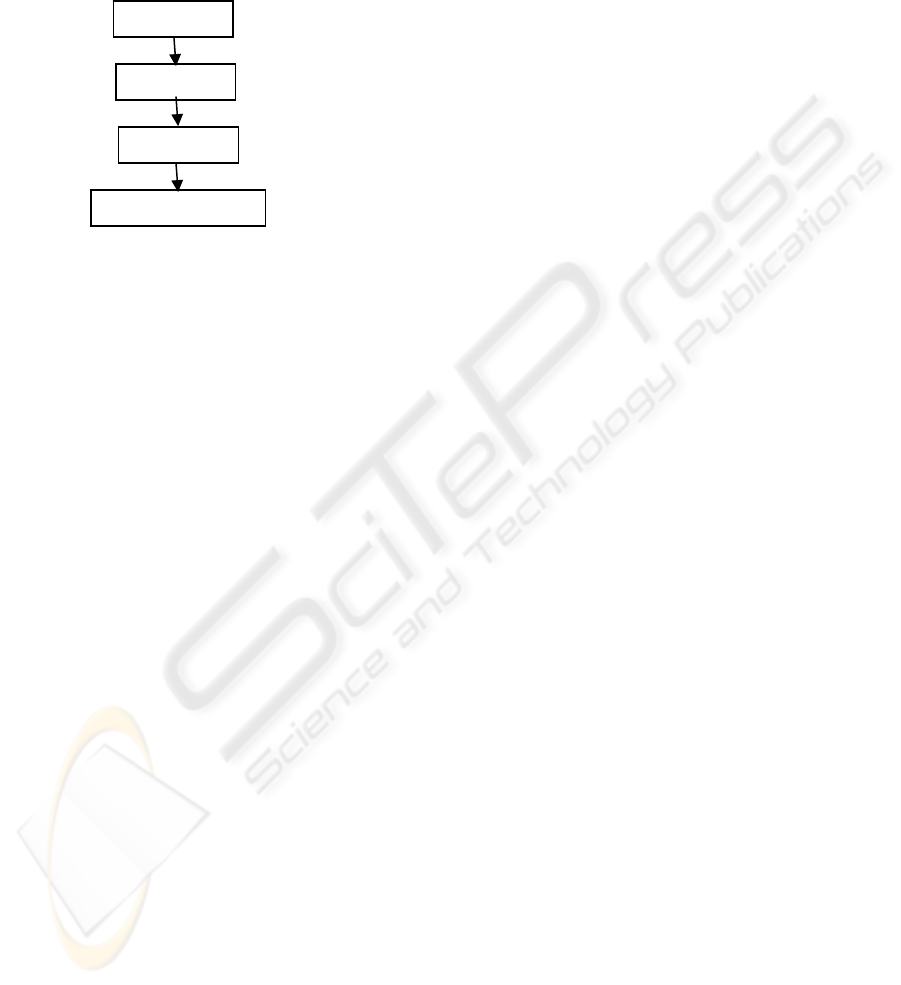
2 THE HIERARCHY

The hierarchical structure (Figure 1) is assigned to

obtain the relevant design illustrated in the form of a

Layout. The elements constituting the hierarchy are

discussed as follows.

Primitives or Threads are shapes at an early

stage of development. These primitives are simple

and unsophisticated. A set of primitives consists of

176

Khanna P., Tandon P. and G. Dhande S. (2007).

HIERARCHIC MODELING OF SYMMETRIC GEOMETRIES.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 176-179

DOI: 10.5220/0002077601760179

 SciTePress

simple two-dimensional geometrical elements like

point, line, arc, circle, ellipse, free-form curve, etc.

Motifs are developed by arranging these

primitives in some order according to some rules. A

motif is the primary unit of the design that gets

replicated to form one block of the design.

Figure 1: Hierarchical Structure of Design.

Pattern is an arrangement of motifs especially as

a decorative design on clothes, carpets, etc. A

pattern of a design is the basic unit from which the

entire design can be obtained. A pattern can be

represented hierarchically as a rooted tree with

nodes representing combinations and instances

primitives. Children of a node represent

substructures within the structure that is represented

by the parent node.

Layout is the final artistic design which a

designer intents to create. In a layout, a finite pattern

undergoes an infinite/finite, static/dynamic repetition

that displays at least combinatorial regularity.

3 DESIGN MODEL

A shape grammar is 2-tuples: SG = (S, R). The

design world vocabulary is represented as a catalog

of shape classes S = (X

, X

, …, X

). A shape

class X

is defined in the catalog S as a 3-tuple i..e.

= (C, Pt, Sz) , where

• C is the name of the shape class

• Pt is a point that specifies the position parameter

• Sz is a list that specifies the size parameters.

For example, a shape class X, and its instances

can be represented as an item in the shape catalog

as: (X (1.0 ,1.0, 0.0) (0.5, 0.5)) where

• X is the name of the shape class

• a position parameter (1.0, 1.0, 0.0) given by a

central reference point,

• a size parameter (0.5, 0.5) such as length, width

of the bounding rectangle.

R is set of shape grammar rules, and is a 2-tuple.

R = (LR, HR), where HR are the high level rules

different for each and every designs and LR are the

low level rules i.e. transformation rules, defined as

LR = (Tr, Sl, Rot) such that

• Tr is the translation of the shape.

• Sl is the scaling of the shape.

• Rot is the rotation of the shape.

Let Pr the primitive, M the motif, P the pattern

and L the layout class of a design. In matrix form

[Pr

] = [S]

] = [Pr

,…,Pr

][R]

] = [(Pr

…

,Pr

) ^/

…

)][R]

] = [(Pr

q,…

,Pr

) ^/

v,…

) ^/

t, ,

)][R]

where: i = 1,2,3,4… is a set of non-negative integers

a, d, j, n, x, l, t, v, h are any non negative integers

and ^/

is and/or operator.

4 MODELING OF MOTIFS

Shape descriptor classifies the motifs as:

4.1 Simple Motif

A simple motif has following structure:

i Geometrical Description: Motifs are described

here in terms of primitives. A motif may consist

of simple two-dimensional primitives and local

transformations. A motif may be empty also.

This is to allow motifs that are not meant to be

rendered but to be used as templates for

positioning other shapes. The exact

representation of this description is

implementation dependent.

ii List of Transformations: Each transformation

in the list is represented as homogeneous

transformation matrix The transformation list

may be empty also.

iii Local Coordinate System: The motif

description and the transformations use a

coordinate system that is local to that motif.

iv Set of Motif Attributes: Attributes considered

to convert hierarchical mathematical models to

physical models are: line thickness, line color,

fill color, fill pattern, etc. The exact details of

attributes and the associated semantics are taken

care at the implementation stage.

out

Pattern

Motif

Thread/Primitive

HIERARCHIC MODELING OF SYMMETRIC GEOMETRIES

177

4.2 Compound Motif

A compound motif is a list of references to other

motifs and some flags to specify the semantics of

utilizing the list. Depending on the flags, compound

motif behaves as one of the following:

(i) Aggregate: Aggregate compound motif is just a

collection of motifs from the simple motif list. It

models itself by asking all its sub-motifs to

render themselves one by one.

(ii) Pattern: Pattern treats the motif list in a special

way. The first motif is treated as Base-Motif and

the rest as Repeat-Motifs. While modeling,

transformation list is requested from Base-Motif

and Repeat-Motifs are generated with one

Repeat-Motif per transformation. If the numbers

of transformations are more than the number of

Repeat-Motifs, the Repeat-Motifs are treated as a

circular list. For each transformation in the list,

the steps include (a) transformation of the current

coordinate system, (b) Selection of next Repeat-

Motif and its generation, and (c) Undoing the

transformation done to the coordinate system

5 PATTERN TREE

Motifs interact with each other forming a hierarchic

structure called pattern. To form a pattern, motifs are

declared. Some of them are simple and some are

compound. This leads to a hierarchy of motifs,

which can be represented as a pattern tree. The

internal nodes represent compound motifs and leaf

nodes represent simple motifs. Figure 2 shows two

samples of motifs and the resultant patterns.

Figure 2: Modeling of Motifs and Patterns.

6 IMPLEMENTATION

The pattern tree has been implemented using C++

language. The NURBS++ library is used for curve

manipulations. NURBS++ is a free C++

implementation of NURBS curve providing a vast

array of operations on the curve.

Adobe Post Script format is used for the output.

PostScript is a powerful page description language

that can be used to produce high quality printed

outputs. GUI is also provided for editing the pattern

tree. It uses GTK--, the C++ version of GTK, and

the GIMP tool kit, for the user interface elements

also known as widgets. GTK-- is chosen for its well-

defined API interface and ease of use.

6.1 Shape Description Format (SDF)

SDF is an ASCII file format that describes simple

motifs in terms of interpolated curves and compound

motifs in terms of simple motifs. Interpolated curves

were chosen since they can represent the common

primitives in floral patterns easily. Also the points

for interpolation can be determined easily by

drawing the primitives on a graph paper. Such

primitives include curved lines, petal outlines, leaf

outlines, etc. The SDF consists of:

Global Attributes and Parameters: This section

contains global attributes for rendering motifs. These

are used if the motifs themselves do not have their

own attributes. Also some transformations are

allowed to allow overall effects on the pattern, such

as adjusting its position on the output page, scaling

entire pattern, etc. Page size can also be specified.

Simple Motif Description: This consists of

geometric description of curves that make the motif.

The curve is specified by means of a list of points

lying on that curve. The points are interpolated as

and when needed to get a NURBS curve. The list of

transformation points can also be specified. Optional

attributes can be specified to alter line color, line

width and fill color of the motif.

Compound Motif Description: Compound

motifs are specified as lists of other motifs. Other

motifs are referred to by their motif_id which is

unique to every motif. Optional flags can be

specified to alter the behavior of the compound

motif as discussed in pattern model.

Render Requests: Render request is simply a

directive to the program to add the motif to a list of

motifs. The list is used for rendering when the

pattern tree is ready.

These entities can occur in any order in the file.

Motif

Pattern

Motif

Pattern

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

178

6.2 Working of the Program

The program builds table of motifs by adding motifs

to it in the order as they are described in the SDF

file. It takes care that motifs are described before

they are used to describe other motifs. It also reports

any errors that may be present in the SDF file.

The program also builds a render list that

includes references of shapes that are requested to be

rendered. After reading the whole SDF file, the

program proceeds to render all motifs in the render

list one by one. To render a motif, its Post Script

output method is called. Compound motifs call the

Post Script procedures of their sub-motifs after

transforming the coordinate system by required

transformation matrices and undo the transformation

after the call. The program takes care of other details

in the Post Script file, such as Document Structuring

Comments (DSC) headers and footers in the file.

Some sample outputs of complicated patterns are

shown through Figure 3, Figure 4 and Figure 5.

Figure 3: A Design with Rectangular and Circular floral

Distribution.

Figure 4: A Design using Multiple Compound Motifs.

Figure 5: A Rectangular Floral distributed Pattern.

7 CONCLUSIONS

In this work, designs are described in terms of

patterns, patterns in terms of motifs and motifs as a

combination of primitives. Motifs are abstract

entities that can produce a visual output and that can

return a list of transformations to attach sub-motifs

to them. A hierarchy of motifs can be built to

produce complex patterns. The model is

implemented as a SDF that allows a user to describe

motifs in terms of interpolated curves.

There are limitations as to what patterns the

model can accommodate due to the fact that pattern

designs are of virtually infinite types and

complexities. The proposed model can efficiently

encode those patterns, which can be easily thought

of as primitives repeated along a path, a periphery or

some other regular arrangement that is independent

of the primitives. Although other pattern designs

may be fitted into this form, the specification of

motifs can be tedious.

Another limitation of the model is that the

transformation points are generally not tied to a

motif’s geometric description. Thus editing the motif

description does not automatically change the

transformations of that motif accordingly. However,

this is a tradeoff. Allowing transformations to be

totally unrelated to the geometrical description of

motif provides extra flexibility in defining patterns.

The model does not take into account the space

occupied by motifs. If some motifs overlap, the

model cannot detect the overlap.

REFERENCES

Cohen, M. F., Shade, J., Hiller, S., Deussen, O., 2003.

Wang Tiles for Image and Texture generation, ACM

Transactions on Graphics, Vol.22, No.3, pp.287-294.

Glassner, A., 2000. Texturing With Symmetry, Glassner’s

Notebook in IEEE Computer Graphics & Application.

Glassner, A, 2004. Crop Art, Part 1-3, IEEE CG&A,

Vol.24, No.5, pp. 86-99.

Kim J., Pellacini F., 2002. Jigsaw Image Mosaics,

Proceedings of Siggraph, ACM Transactions on

Graphics, Vol.21, No.3, pp. 657-664.

Tarasov L., 1986. This Amazingly Symmetrical World, Mir

Publishers, Moscow.

Wolfe J., (Ed.), 1996. Border Pattern Gallery,

www.math.okstate.edu/wolfe/border/border.html

HIERARCHIC MODELING OF SYMMETRIC GEOMETRIES

179