EXPLOITING COUPLED JOINTS
Anatomic Control of the Spine with IK Through Linearly Coupled Joints
Daniel Raunhardt and Ronan Boulic
VRLAB, Ecole Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
Keywords: Inverse kinematics, joint coupling, human modeling, articulated figure.
Abstract: In this paper we propose a simple model for the coupling behavior of the human spine that is capable of
exhibiting anatomically correct motions of the vertebrae in virtual mannequins. Such a model transparently
integrates in our inverse kinematics framework as it couples standard swing and revolute joint models. The
adjustment of the joints due to the coupling is made with several simple (in)equality constraints, resulting in
a reduction of the solution space dimensionality for the inverse kinematics solver. A key benefit is to
prevent the inverse kinematics algorithm from providing infeasible postures. We exploit how to apply these
simple constraints to the human spine by a strict decoupling of the swing and twist motion of the vertebrae
and demonstrate the validity of our approach on various experiments.
1 INTRODUCTION
Realistic animations of human characters play an
important role for interactive applications. Three
dimensional virtual mannequins are the common
representation of the graphical interface, serving as
an interactive character inside the virtual
environment (Magnenat-Thalmann et al. 2004)
(Philips et al. 1990). Often researchers improved the
representation and animation of the exterior skin and
muscle deformations of the virtual mannequins
(Wilhelms et al. 2002) while the model of the
underlying body has been kept unchanged.
However, increasing the surface details of the virtual
mannequins may lead the viewers to be more
sensitive to unrealistic joint motions in animations
such as in the shoulder and spine regions of the
human body (Hodgins et al. 1998).
Joint models are important for correct motion
analysis of tasks, including the estimation of muscle
lengths and moment arms (Delp et al. 1995).
Introducing accurate biomechanical joint models to
the traditional hierarchy of joint transformations can
lead to an improved realism in human character
animation. Anatomical axes of rotations and joint
centers of the human body are taken from literature
and refined to produce improved fidelity of the
motions.
In this paper we introduce a human spine model
based on a set of coupled vertebral joints that reflect
its anatomic mobility distribution (Kapandji
1982a)(Kapandji 1982b). The vertebral joints are
coupled through linear equality constraints allowing
to transparently integrate the spine model within an
existing inverse kinematics (IK) solver. Each
equality constraint reduces the solution space for the
inverse kinematics solver. Relatively few parameters
are necessary to control the complex articulation of
the human spine. We give a short introduction to our
inverse kinematics solver based on the Prioritized
Inverse Kinematics (Baerlocher et al. 2004) and
demonstrate the validity of our model with different
experiments including performance measurements.
2 PREVIOUS WORK
The first use of articulated joint models for
representing human joints can be found in studies of
kinematics of robotic manipulators. These systems
used the Denavit-Hartenberg link parameter notation
from robotics to represent virtual mannequins with
articulated limbs (Girard et al. 1985). Although the
notation to associate coordinate frames between
adjacent segments is convenient, each parameter set
describes only a single degree of freedom (dof)
between two segments. Multiple dofs can be
achieved by combining multiple sets of parameters.
Structures like the spine exhibit a high degree of
13
Raunhardt D. and Boulic R. (2007).
EXPLOITING COUPLED JOINTS - Anatomic Control of the Spine with IK Through Linearly Coupled Joints.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 13-20
DOI: 10.5220/0002077900130020
Copyright
c
 SciTePress

coupling behavior. This coupling behavior of the
spine has been exploited by Monheit et al. (1991) to
develop a kinematic model of the spine that exhibits
flexion-extension, lateral bending and axial torsion
rotation. For a normalized representation of the
human skeleton Kulpa et al. (2005) modeled the
spine with a spline that could be divided into
segments. To retrieve the positions of the vertebrae,
the spline representing the spine is simply
discretized according to the distances of the
vertebrae.
Apart form the spine itself, Maciel et al. (2002)
incorporate joints that can translate and rotate
together on plane and where the joint limits
dynamically change with the dofs of any joint.
Herda et al. (2005) characterize the joint coupling
behavior by implicit surfaces obtained from motion
captured values. This representation allows to
characterize intra- and inter-joint dependencies but
is not a very intuitive way to control the human
motion of the joints. To restrict the joint angle
ranges for ball-and-socket joints spherical polygons
(Korein 1985) and joint sinus cones (Maurel et al.
2000)(Wilhelms et al. 2002) have been introduced.
Spherical polygons are more general than cones but
they are also more complex to deal with. Cones are
often sufficient to represent the human joints
(Korein 1985).
Like our approach the Peabody system (Badler et
al. 1993) collects joints into different groups of
joints that have group angles to configure the joint
groups’ segments. Shao et al. (2003) introduced a
general joint component model called joint maps
that allows modeling of joint expressions over
several bone segments for biomechanical accurate
joints. A joint map is a function that takes a set of
inputs (e.g. set of joints) to produce output for one or
more joints. The input can be seen as the dofs and
the outputs are the modified joint values (e.g. angle,
translation variations). The outputs of one joint map
can be combined with the inputs of another joint
map to create increasingly sophisticated behaviors.
The process that performs this mapping varies
according to the type of the desired joint behavior.
Seen from this variety of presented joint models,
a single joint model representation is not suitable for
capturing all the different characteristics of the
human joints. In fact, specialized joint models are
often needed.
In contrast our model uses common joint models
such as revolute (1 dof) or swing (2 dofs) joints for
inverse kinematics. Through coupling we group the
joints into sets and reduce the remaining solution
space for the inverse kinematics solver. The paper
focuses especially on the case of the spine but it can
be used for a wide range of other cases. The spine
case is especially interesting because the mobility
allowed by the vertebrae shape is changing all along
the spine. For this reason we separate the handling
of the swing and the twist components. This allows
producing anatomically correct postures.
3 PRIORITIZED INVERSE
KINEMATICS
3.1 Constraining the Solution
We provide here only a brief overview of the
Prioritized Inverse Kinematics algorithm (PIK) that
handles an arbitrary number of priority levels and
linear constraints for the purpose of controlling
virtual mannequins or robot manipulators. In this
approach the articulated structure is organized as a
tree of chains. In the specific case of the human
body we are compliant with the H-Anim standard
(Humanoid Animation Working Group) that
includes all human joints.
As the joint models are independent of each
other, possible coupling, due to the presence of
tendons or muscles spanning over several joints, is
defined as additional “hard” constraints. This is
achieved through equality constraints acting on the
coupled joint parameters. We exploit also inequality
constraints for two purposes: to model the limit
range of a single joint or to offer a “relaxed”
coupling between joints.
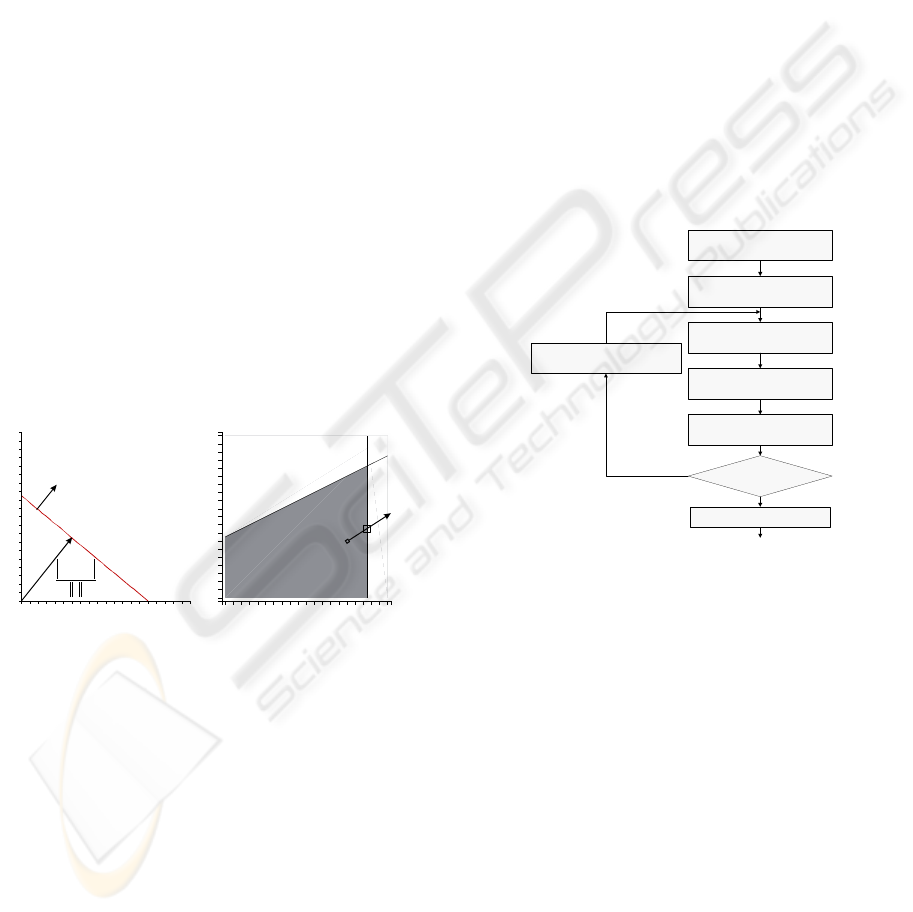
Let us recall the definition of linear equality
(Figure 1 left) and inequality constraints (Figure 1
right) for a joint configuration q with n dofs:
i
T
i
bqc = for gi ..1=
(1)
i
T
i
bqc ≤ for gi ..1=
(2)
where the
i
c are n-dimensional vectors and the
i
b are scalars. Equation (2) allows simple lower
bounds and upper bounds on joint variables, as well
as linearly coupled joint limits. This set of
constraints defines a convex space of feasible
configurations. The choice of linearity is due to the
higher complexity introduced by non-linear
constraints. Joint limits that should never be violated
are handled as inequality constraints while we model
the anatomical joint coupling generally by equality
constraints.
The general PIK algorithm relies on an efficient
computation of projection operators enforcing tasks
grouped into an arbitrary number of strict priority
levels. The management of the (in)equality
constraints must be integrated within the process that
computes the joint variation. Ignoring the constraints
for the computation of the joint variation and only
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
14

adjusting the resulting joint configuration to satisfy
the constraints leads to non optimal solutions
(Baerlocher et al. 2004). The linear equality
constraints can be ensured within a single iteration
step at the initialization phase of the joint variation
computation. To achieve this we modify the initial
projection operator P
0
so that the resulting solution
space lies on the constrained subspace. Secondly, the
initial joint variation, noted ∆q
0
, is set to the
displacement required to meet the constraints, if this
is not already the case. This second term helps also
to avoid numerical drift away from the constraints.
Compared to the PIK algorithm described in
(Baerlocher et al. 2004), these additional “hard”
constraints can be seen as tasks of “infinite” priority
(i.e. of higher importance than any other task)
shaping the solution space. The initial projector
operator P
0
remains constant as long as no equality
constraint is added or removed.
procedure init_projector
begin
P
0
= I
n
for all equality constraint do
if (¬conflicting constraint)
P
0
= P
0
– P
0
(c*c
T
)
end if
end for
end
6420
8
6
4
2
0
8
1
q
2
q
3065
21
=+ qq
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
6
5
c
0
2
86420
8
6
4
2
q
1
q
7
1
≤
q
k
q
tr
y
k
qq
Δ
+
1
+
k
q
62
21
≤+− qq
c
bqc
T
−
Figure 1: Left: equality constraint between two joints q
1
and q
2
. Right: the grey region indicates the possible area
of solutions for the joints q
1
and q
2
. The computed
solution q
k
+∆q
try
violates the inequality constraint q
1
≤ 7,
so the corrected solution is clamped to q
k+1
.
The inequality constraints are checked after the
new joint configuration q
k+1
is computed, where the
new joint state is defined as the sum of the current
configuration and the computed solution q
k
+∆q.
Figure 1 (right) illustrates a case where the new
configuration violates an inequality constraint
modeling a joint limit; therefore a new equality
constraint is dynamically added into the constraint
set, called the working set, to clamp the
corresponding joint on the limit. In our model we
check first the user-defined inequality constraints
and afterwards the joint limits. This gives the user-
defined inequality constraints a higher priority over
the joint limits. The prioritized solution is re-
evaluated as long as no additional inequality
constraint is violated (Figure 2). This loop is
necessary to guarantee the tasks’ error minimization.
The cost of the clamping loop is linear to the number
of recruited joints (see section 3.2). In the worst case
each clamping iteration would handle a single
clamped joint. This is seldom the case as, very often
multiple joints violate their limit simultaneously
which is handled through a single clamping
iteration.
If two (in)equality constraints are conflicting, i.e.
they cannot be satisfied at the same time, we
consider only the constraint that has been first added
to the working set of the constraints (e.g. the user-
defined inequality constraints dominate the joint
limits). Thus, we may get a solution of the joint
variation that may violate some of the constraints.
Initialization: All equality constraints (if
any) are introduced in the working set.
Build joint variation for all priority levels
Check user defined inequality
constraints
At least one inequality
constraint violated?
end
The new configuration can be kept
Select the violated constraint which is
closest to the initial configuration and add
it to the working set
Compute inital projector operator and
joint variation
Check joint limits (modeled as inequaliy
constraints)
yes
no
Figure 2: The Prioritized Inverse Kinematics convergence
loop highlighting the construction of the joint variation
solution for multiple priority levels and the management
of the equality and inequality constraints.
3.2 Joint Recruiting Level
Our PIK allows a task to recruit all or part of the
joints from its parent up to the root of the articulated
structure. We can manually discard joints that
should not participate to achieve the task. For
example, whenever controlling the position of the
wrist it is important to decide whether the spine
should participate or not. The problem of
overlapping joint regions has first been described by
Badler et al. (1980). Normally to resolve this
problem a minimal joint recruiting rule for joints
shared by multiple tasks has to be enforced (Le
Callennec et al. 2006). This rule concerns those parts
of the articulated structure where multiple tasks may
recruit part of their joints. Let T
i
be a task of priority
EXPLOITING COUPLED JOINTS - Anatomic Control of the Spine with IK Through Linearly Coupled Joints
15

i, Rec(T
i
) the corresponding set of recruited joints
and Anc(T
i
) all the possible joints that may be
recruited by T
i
(from its parent up to the root). Then,
for any two priority levels a>b we must have:
Rec(T
b
) ∩ Anc(T
a
) ⊂ Rec(T
a
)
(3)
Equation (3) states that recruited joints of low
priority tasks are a subset of high priority tasks.
Without this rule, it may lead to diverging solutions
where a low priority task dominates a high priority
task. Equation (3) solves the problem of overlapping
regions only if there are no joints coupled by
(in)equality constraints. The first problem using
coupled joint is that joints can be implicitly
recruited. If a joint is recruited by the task T
i
and if
this joint is also coupled to other joints, all these
coupled joints are implicitly recruited by task T
i
. A
joint recruited by a low priority task can be coupled
to a joint that is only recruited by high level priority
task. Thus, the low priority task would gain
influence over the high priority task despite
Equation (3) is satisfied. The set of all implicitly
recruited joints due to coupling of a task T
i
is
defined as Coup(Rec(T
i
)). The second problem is
that joints are coupled that are not recruited by any
task. Thus, we extend the Equation (3) to the
following conditions for the recruiting level for any
two priority levels a>b:
(Rec(T
b
) ∪ Coup(Rec(T
b
))) ∩ ( Anc(T
a
)
Coup(Rec(T
a
))) ⊂ Rec(T
a
)
(4)
U
Coup(Rec(T
i
)) ⊂
U
Rec(T
i
)
(5)
Equation (4) ensures that coupling can only take
place from the joints up to the root of the articulated
structure and that a lower priority task cannot couple
a joint that is nearer to the root than a higher priority
task. Equation (5) states that only joints recruited by
task are allowed to be also coupled by constraints.
4 SPINE
4.1 Introduction
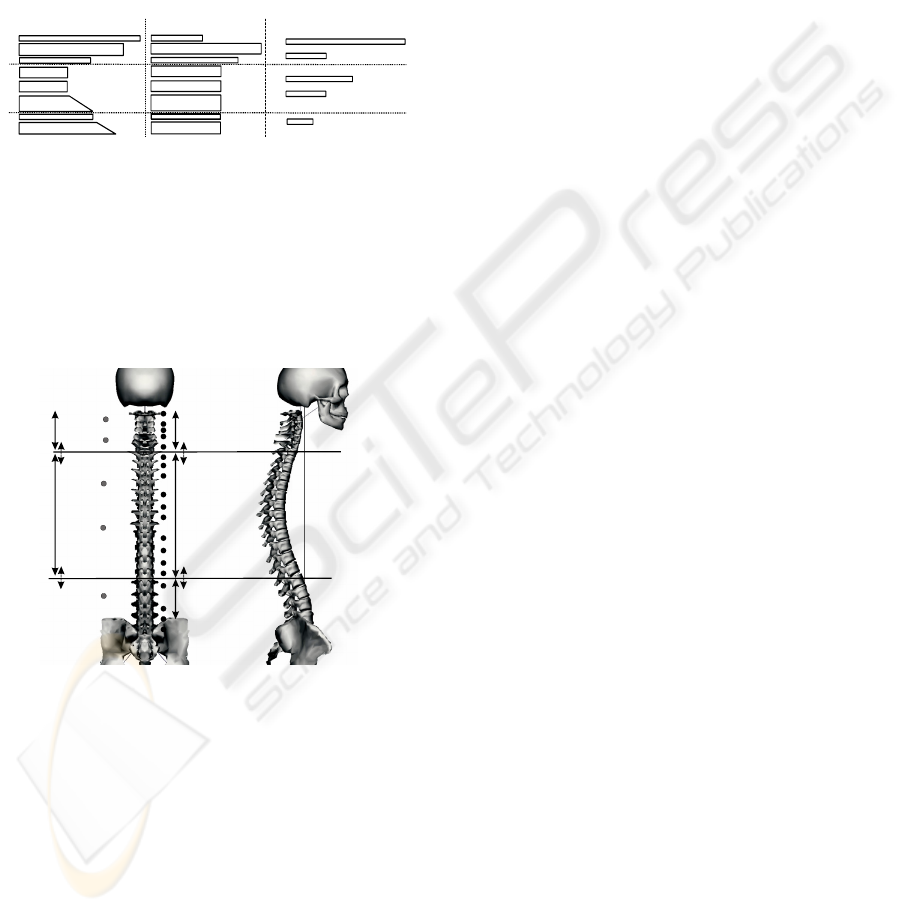
The human spine consists of twenty four movable
vertebrae. According to positions and the
functionality of the individual vertebrae, the spine
can be divided into three sets: the cervical region
(seven vertebrae in the neck), the thoracic region
(twelve vertebrae in the thorax), and the lumbar
region (five vertebrae in the abdomen) (Kapandji
1982a) (Kapandji 1982b) (Monheit et al. 1991).
Each vertebra has three dofs of rotation (flexion-
extension, lateral-bending and torsion). These three
rotational components may have quite different
rotation centers and non-orthogonal rotation axes.
Modeling each vertebra as a joint without taking into
consideration the coupling that exists among them
due to the rotational behavior is not recommended as
too much freedom is left in the spine for the inverse
kinematics solver. This choice usually leads to
unrealistic spine postures. It is preferable to use only
a few uncoupled joints strategically placed on the
spine, in order to have a more realistic rigidity of the
system. Thus, we simplify the control of the spine
movement by a simple reduction of the dofs.
4.2 Spine Model
As each vertebra allows a swing motion (flexion-
extension, lateral-bending) and a torsion motion
(rotation along vertical vertebrae axis) the general
solution would be to represent each vertebra by a
ball-and-socket joint (3 dofs). Euler angles,
quaternions or exponential maps are often used to
express these segment orientations. The use of
quaternions or the exponential map for inverse
kinematics is advantageous compared to Euler
angles as they have no singular configuration within
their mobility range (Grassia 1998). For this reason
our inverse kinematics solver represents the joints as
exponential maps. The drawback of the exponential
map for the coupling with linear (in)equality
constraints is that it would not be possible to couple
independently the swing components or the twist of
two ball-and-socket joints as by changing the swing
of a ball-and-socket joint the torsion of this joint
may be changing too. To control separately the
swing and twist of the joints we have chosen to
consider two distinct joint types: swing (2 dofs) and
revolute (1 dof). The swing joint model is an
exponential map vector with zero contribution along
the main spine axis (no twist). It models the
flexion/extension and lateral bending of the
vertebrae while the revolute joint is oriented along
the spine main axis to model the twist mobility (also
called the torsion). These joints are strategically
placed over the spine as seen in Figure 3. Owing to
this organization we obtain a great flexibility in the
coupling schemes. For example, we may couple the
torsion of a joint with the lateral-bending of another
as happens in the cervical spine (White et al. 1990).
Thus, we are able to fully control the coupled
behavior of the spine by two common joint models
and simple (in)equality constraints.
For interoperability we have chosen to use the
same joint names as defined in H-Anim (Humanoid
Animation Working Group). As in the lumbar region
the torsion is equally distributed (Kapandji
1982a)(Kapandji 1982b) and its amount is very
small, we have placed only one revolute joint in this
region. In the thoracic and the cervical region we
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
16

have placed more revolute joints according to the
corresponding bigger torsion ranges. The concrete
coupling coefficients are based on the vertebrae
value ranges and their human coupling behavior
(Kapandji 1982a)(Kapandji 1982b). Table 1 presents
our choice of the joint ranges based on our
strategically placed joints over the spine.
Table 1: Joint ranges of the spine at different levels of the
spine along the three anatomic axis (Kapandji 1982a)
(Kapandji 1982b).
Flexion/Extension
Lateral bending
Torsi on
Thoracic
Lumbar
Cervical
vl5-vl3
vl2
vt12-vt9
vt7-vt5
vt3-vt1
vc7
vc5-vc3
vc1
vc3
vt4
vt8
vt2
vc6
To keep some independent movement between the
individual regions of the spine (lumbar-thoracic,
thoracic-cervical) we couple two regions with
inequality constraints as illustrated in Figure 3. This
helps the regions to behave more independently than
with a strict coupling by equality constraints.
Nevertheless we can ensure a fluent transition
between two regions.
Lumbar region
T horacic region
Cervical region
Equality constraint
Equality constraint
Equality constraint
Inequality constraint
Equality constraint
Inequality constraint
Inequality constraint
Inequality constraint
Swing Joints
Torsion Joints
Figure 3: Our human spine model with the different spine
regions. We have strategically placed some rotational
joints (indicated by gray circles) to model the torsion of
the spine where for the remaining joints we use swing
joints (indicated by black circle). Inside a region we
couple the swing joints by equality constraints. To keep
some independency between the regions we use inequality
constraints.
The problem that arises with this concept is that the
equality constraints and the inequality constraints
(user-defined for the regions or joint limits) may be
conflicting. To avoid such conflicting we do only
check the joint limits for the first joint in each spine
region (for swing: vl5, vt12, vc7; for twist: vl2, vl8,
vc6). The accordance to the joint limits of the other
joints is automatically given by the use of real
measured vertebrae value ranges and human
coupling coefficients. The drawback of inequality
constraints is that they can lead to a re-evaluation of
the joint variation solution.
4.3 Summary
To summarize, our spine model is composed of three
segments. We strictly decouple the swing and twist
of the vertebrae using only swing and revolute
joints. Within each segment we couple the joints by
equality constraints, while the different segments are
connected by inequality constraints. A simple joint
coupling with equality constraints inside each spine
region would leave only 3 dofs (1 for
flexion/extension, 1 for lateral bending and 1 for
torsion) to each region. This would make a total of 9
dofs to control the entire spine which is considerably
less than the 72 dofs in an uncoupled spine.
Although our model is probably still not as accurate
as a real human spine, we can achieve fairly more
realistic spine configurations than in an uncoupled
spine. We think that our spine model is a good
compromise between the accuracy and the simplicity
of control.
5 RESULTS
5.1 Isolated Spine
This experiment highlights the behavior of our
approach with two conflicting tasks on an isolated
spine consisting of 24 vertebrae where the vertebrae
are coupled with 32 equality and 12 inequality
constraints. Figure 4 on the left shows the initial
configuration of the spine. We have defined a
position and an orientation task to be achieved. The
orientation task is modeled as a high priority task
while the position task has low priority. We
executed this experiment twice, once with the
coupled spine and once where the joints of the spine
can move independently within their independent
joint limits.
Figure 4 highlights the initial position, the
achieved configuration for the spine without
coupling and with coupling. The obvious problem of
the uncoupled spine is the strong change of the spine
shape while the coupled spine displays no abrupt
changes of the shape. This behavior of the
uncoupled spine is possible due to the lack of
coupling, each joint being able to move
independently without taking into account the
motion of other joints. We have also compared the
computational speed, the error convergence and the
EXPLOITING COUPLED JOINTS - Anatomic Control of the Spine with IK Through Linearly Coupled Joints
17

norm of the joint variations of the two methods
(Figure 5).
orientation tas
k
Without coupling Coupling
front left front left front left
p
o
s
i
t
i
o
n
t
a
s
k
Initial posture
initial
orientation
Figure 4: Front and left side views of the isolated spine:
(left) initial configuration with indications of the two
tasks; (middle) end configuration without coupling; (right)
end configuration with coupling.
0
10
20
30
40
50
60
70
80
90
100
0 5 10 15 20 25 30
Iteration
Error [%]
0
0.05
0.1
0.15
0.2
0.25
0.3
Time [s] / Norm [rad]
Error no coupling
Error coupling
Norm coupling
Norm no coupling
Time no coupling
Time coupling
Figure 5: Comparison between coupling/no coupling for
computational time and error convergence.
Coupling with equality constraints reduces the
solution space for the inverse kinematics solver.
Therefore the error convergence could be slowed
down or the task may not be achievable while
without coupling it would be possible. In this
experiment the position task with coupling cannot be
fully achieved, so the final error does not converge
to zero. Overall the total computational time shows
some advantages for our coupling approach. By the
pre-computation of the initial projection operator the
computational overhead is limited to adjusting the
initial joint variation before each iteration. We have
measured that around 3-8% of the total
computational time for one iteration are spent to
initialize the joint variation. But as we remove some
dofs for the inverse kinematics solver this
computation stage is cheaper; in the end we gain
some computational time compared to the approach
without coupling (cf. “Error no coupling” and “Error
coupling” curves in Fig. 5). Due to coupling we also
restrict the overall joint variation during the
convergence (cf. “Norm no coupling” and “Norm
coupling” curves in Figure 5).
No_coupling
Coupling
Thoraric
Lumbar
Cervical
Figure 6: Distribution of the swing components of the
vertebrae for coupling/no coupling.
The swing components s
x
(flexion-extension) and s
y
(lateral-bending) are presented in Figure 6. The
swing component values without coupling are
widely distributed in the s
x
-s
y
space which leads to
the change of the signs in the spine as presented in
Figure 4 in the middle. On the other hand the swing
component values of the vertebrae with coupling are
grouped per spine region and can only change
significantly between two regions. Another problem
of the uncoupled spine is the abrupt change of the
torsion direction which is discussed in detail in
Section 5.2.1.
5.2 Full Body Postures
A spine model of 24 vertebrae may be too time
consuming for real-time applications of virtual
mannequins especially if there are other time
consuming calculations such as skinning or collision
detection/response. Thus, a simplified spine model is
often used. In the next experiments the uncoupled
simplified spine consists of 8 ball-and-socket joints
with a total of 24 dofs. The lumbar and the thoracic
region are each represented with three joints while
the cervical region has only two joints. As already
mentioned our coupled spine model can only be
represented by swing and rotation joints. Our
coupled spine model is built by 8 swing joints and 5
rotational joints. Figure 7 illustrates the initial
posture for the next experiments.
5.2.1 Bio-mechanical Considerations
In this experiment the virtual mannequin with the
simplified spine has to achieve a simple balanced
posture. The toes of the right foot are attracted
toward a position in the back while the hands have
to reach a position in the front. These goals are
modeled with a middle priority position task. During
the whole motion the left foot has to stay on the
ground which is reflected by two high priority tasks
(one for the toes and one for the heel). A low
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
18

priority orientation task is used to maintain the head
looking forward. To keep the virtual mannequin in
balance we project the center of mass over the left
foot with the highest priority task. We executed this
experiment twice, once with our coupling approach
and once with independent vertebrae (Figure 7
right).
Without
coupling
Coupling
Initial posture
Figure 7: The initial and the achieved postures without
coupling and with coupling.
Although both methods are visually similar there is
an important difference. In the uncoupled spine there
is an abrupt change in the torsion direction.
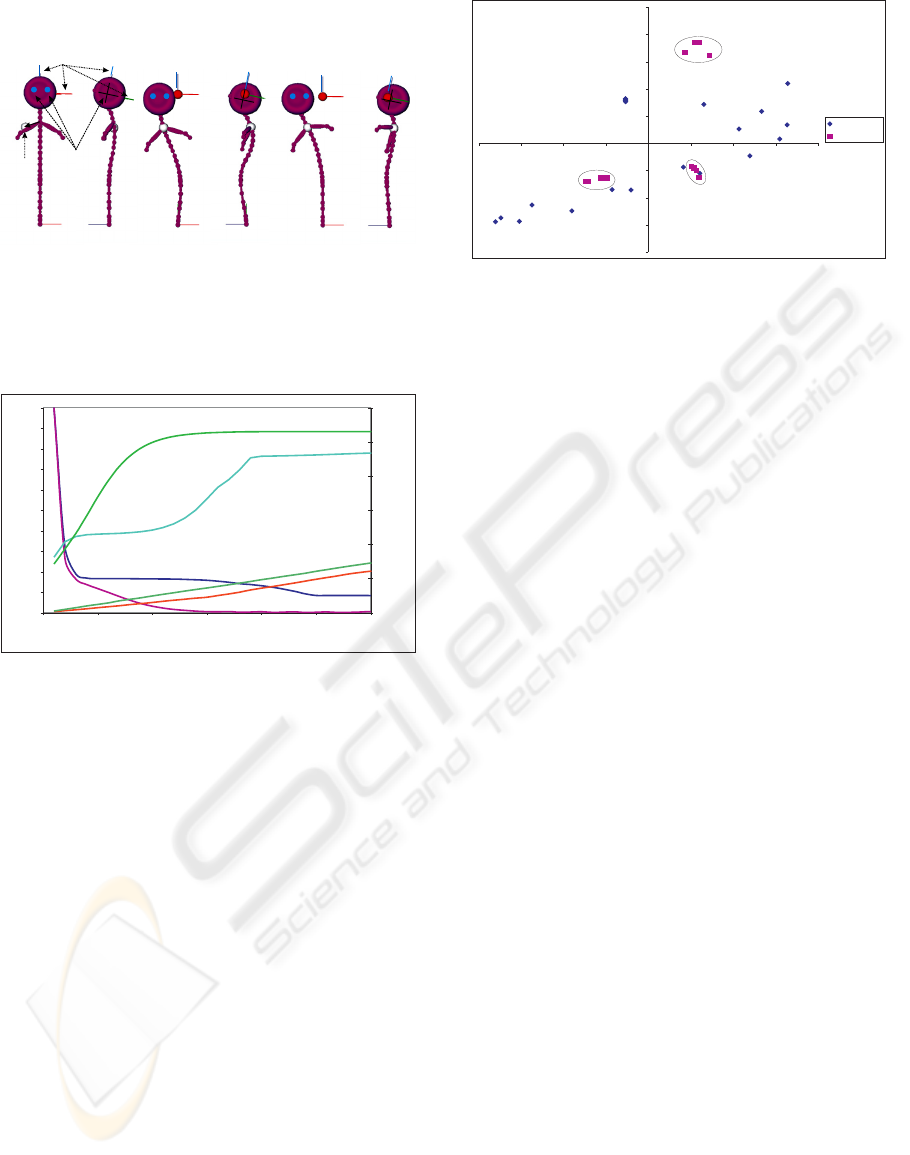
Considering three successive vertebrae (Figure 8
left), the lowest vertebrae may have a torsion to the
right, the middle to the left while the third vertebrae
rotates again to the right.
Figure 8: Possible changes of the torsion direction of
vertebrae for an uncoupled spine (left) and corresponding
measured values for uncoupled spine (middle) and
coupled spine (right).
We have measured a similar behavior of the
vertebrae torsion directions for the uncoupled spine
as illustrated in Figure 8 middle. Such a behavior is
bio-mechanically not possible although a change of
the torsion direction is possible between spine
regions.
For the coupled spine changes of the torsion
direction can only appear for vertebrae which are
coupled by inequality constraints (e.g. between two
spine regions).
5.2.2 Periodic Tasks
This experiment highlights the behavior of coupling
for long periodic tasks. The hands of the virtual
mannequin have to follow a moving goal which
forms an eight in the vertical plane (two low priority
positional tasks are used). The feet have to stay on
the ground (four high priority tasks) and the virtual
mannequin has to keep its balance by projecting the
center of mass between the two feet (highest priority
task). Figure 9 illustrates the different postures
without coupling and with coupling after an
increasing number of cycles.
W
i
t
h
o
u
t
c
o
u
p
l
i
n
g
C
o
u
p
l
i
n
g
W
i
t
h
o
u
t
c
o
u
p
l
i
n
g
C
o
u
p
l
i
n
g
W
i
t
h
o
u
t
c
o
u
p
l
i
n
g
C
o
u
p
l
i
n
g
200 cycles 600 cycles
2000 cycles
50 cycles
100 cycles
W
i
t
h
o
u
t
c
o
u
p
l
i
n
g
C
o
u
p
l
i
n
g
W
i
t
h
o
u
t
c
o
u
p
l
i
n
g
C
o
u
p
l
i
n
g
W
i
t
h
o
u
t
c
o
u
p
l
i
n
g
5 cycles
C
o
u
p
l
i
n
g
Figure 9: Postures on the left without coupling and on the
right with coupling after an increasing number of cycles
(from left to right and top to bottom). The blue bar
indicates the goal of the hands.
At the beginning the two postures are almost
identical. We can observe that the differences
between the postures increase with the number of
cycles. After 2000 cycles the coupled spine has still
a plausible shape while the uncoupled is highly
deformed. This is caused by the drift of the solution
in the joint space as originally discussed by Klein et
al. (1983). Coupling joints by (in)equality
constraints reduces the solution space for the inverse
kinematics solver which counteracts this drift in the
joint solution space for periodic tasks.
6 CONCLUSIONS
In this paper we have proposed a simple method to
model the coupling behavior of the spine. We use
simple (in)equality constraints to reflect the coupling
between the vertebrae. Each equality constraint
removes one dof of the solution space for the inverse
kinematics solver. Relatively few parameters are
sufficient to represent the spine. We have shown that
our approach is able to produce more natural spine
EXPLOITING COUPLED JOINTS - Anatomic Control of the Spine with IK Through Linearly Coupled Joints
19

shapes. By introducing constraints the inverse
kinematics solver may be no longer able to find a
solution with the same error as without coupling due
to the reduced solution space. The coupling may be
too restrictive and not cover the whole space of
possible human spine motion but it provides
plausible postures of the spine and is less sensitive to
the drift of the solution for periodic tasks. Besides
the computational cost is slightly less than for the
uncoupled one. Our future work is to exploit this
model within a real-time posture control of a virtual
mannequin interacting with its environment.
ACKNOWLEDGEMENTS
The authors would like to thank Achille Peternier
and Damien Maupu for their support of the graphics
library. This work has been realized with the support
of the Swiss National Science Foundation under the
grants 200020-109989, and is partially supported by
the E.U. ENACTIVE Network of Excellence.
REFERENCES
Badler, N. I., O'Rourke, J., Kaufman, B. 1980. Special
problems in human movement simulation. In
Proceedings of the 7th Annual Conference on
Computer Graphics and Interactive Techniques
(Seattle, Washington, United States, July 14 - 18,
1980). SIGGRAPH '80. ACM Press, New York, NY,
189-197.
Badler, N. I., Phillips, C. B., Webber, B. L. 1993. Virtual
Humans and Simulated Agents. New York, NY:
Oxford University Press.
Baerlocher, P., Boulic, R. 2004. An Inverse Kinematics
Architecture Enforcing an Arbirtray Number of Strict
Priority Levels. In The Visual Computer, Springer
Verlag, 20(6), 402-417.
Delp, S.L., Loan, P. 1995. A software system to develop
and analyze models musculosketal structures,
Computers in Biology and Medicine, vol. 25, 21-34.
Girard, M., Maciejewski, A. A. 1985. Computational
modeling for the computer animation of legged
figures. In Computer Graphics (SIGGRAPH 1985
Proceedings), B. A. Barsky, Ed., vol. 19, 263-270.
Grassia, F. S. 1998. Practical parameterization of rotations
using the exponential map. J. Graph. Tools 3, 3 (Mar.
1998), 29-48.
Herda, L., Urtasun, R., Fua, P. 2005. Hierarchical implicit
surface joint limits for human body tracking.
Computer Vision and Image Understanding 99(2),
189-209.
Hodgins, J. K., O'Brien, J. F., Tumblin, J. 1998.
Perception of Human Motion With Different
Geometric Models. IEEE Transactions on
Visualization and Computer Graphics 4, 4 (Oct.
1998), 307-316.
Humanoid Animation Working Group, 1999, H-Anim 1.1
specification for a standard humanoid. www.h-
anim.org.
Kapandji, I. A. 1982 a. The Physiology of the Joints:
Upper Limb, 2 ed., vol. 1. Churchill Livingstone.
Kapandji, I. A. 1982 b. The Physiology of the joints : The
Trunk and the Vertebral Column, 2 ed., vol. 3.
Churchill Livingstone.
Klein, C. A., Huang, C. H. 1983. Review of pseudoinverse
control for use with kinematically redundant
manipulators, IEEE Transactions on Systems, Man,
and Cybernetics, Vol. SMC-13, No-2 (March/April),
245-250.
Korein, J. U. 1985 A Geometric Investigation of Reach.
MIT Press.
Kulpa. R., Multon F., Arnaldi B. 2005. Morphology-
independent representation of motions for interactive
human-like animation. Computer Graphics Forum 24,
3 (2005), 343-352.
Le Callennec, B., Boulic, R. 2006. Interactive motion
deformation with prioritized constraints. Graph.
Models 68, 2 (Mar. 2006), 175-193.
Maciel, A.; Nedel, L.P.; Dal Sasso Freitas, C.M. 2002.
Anatomy-based joint models for virtual human
skeletons, Computer Animation, 2002. Proceedings of
, vol., 220-224.
Magnenat-Thalmann, N., Thalmann, D. 2004. Handbook
of Virtual Humans. Wiley. ISBN 0-470-02361-3.
Maurel, W., Thalmann, D. 2000. Human shoulder
modeling including scapulo-thoracic constraint and
joint sinus cones. Computers and Graphics 24, 2, 203-
-218.
Monheit, G., Badler, N. I. 1991. A Kinematic Model of
the Human Spine and Torso. IEEE Comput. Graph.
Appl. 11, 2 (Mar. 1991), 29-38.
Phillips, C. B., Zhao, J., Badler, N. I. 1990. Interactive
real-time articulated figure manipulation using
multiple kinematic constraints. In Proceedings of the
1990 Symposium on interactive 3D Graphics
(Snowbird, Utah, United States). SI3D '90. ACM
Press, New York, NY, 245-250.
Shao, W., Ng-Thow-Hing, V. 2003. A general joint
component framework for realistic articulation in
human characters. In Proceedings of the 2003
Symposium on interactive 3D Graphics (Monterey,
California, April 27 - 30, 2003). SI3D '03. ACM Press,
New York, NY, 11-18.
White, A. A., Panjabi M.M. 1990. Clinical Biomechanics
of the Spine, Philadelphia, J.B. Lippincott Company,
ISBN 0-397-50720-8.
Wilhelms, J. Gelder, A. V. 2002. Fast and easy reach-cone
joint limits. J. Graph. Tools 6, 2 (Sep. 2002), 27-41.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
20