
MULTI-MODE REPRESENTATION OF MOTION DATA
Bj
¨
orn Kr
¨
uger, Jochen Tautges and Andreas Weber
Institut f
¨
ur Informatik II, Universit
¨
at Bonn, R
¨
omerstr. 164, 53117 Bonn, Germany
Keywords: Motion Capture, N -Mode SVD, Dynamic Time Warping, Motion Synthesis.
Abstract: We investigate the use of multi-linear models to represent human motion data. We show that naturally occur-
ring modes in several classes of motion can be used to efficiently represent the motions for various animation
tasks, such as dimensionality reduction or synthesis of new motions by morphing. We show that especially
for the approximations of motions by few components the reduction based on a multi-linear model can be
considerably better than one obtained by principal component analysis (PCA).
1 INTRODUCTION
The use and reuse of motion data recorded by mo-
tion capture systems is an important technique in
computer animation. Usually the motion data are
represented as sequences of poses, which in general
employ skeletal representations of motion data. In
the last few years also data bases of motions have
been used to synthesize or analyze motions in vari-
ous ways, see e.g. (Giese and Poggio, 2000; Troje,
2002; Kovar et al., 2002; Safonova et al., 2004; Kovar
and Gleicher, 2004; Ormoneit et al., 2005; Majkow-
ska et al., 2006).
Whereas the use of temporal alignments of mo-
tion in these data bases is well established (Bruderlin
and Williams, 1995; Giese and Poggio, 2000; Kovar
and Gleicher, 2003; Hsu et al., 2005) and the use of
linear models for representing motions and their di-
mensionality reduction by principal component anal-
ysis (PCA) is also a well established technique in var-
ious contexts (Barbi
ˇ
c et al., 2004; Chai and Hodgins,
2005; Safonova et al., 2004; Glardon et al., 2004;
Troje, 2002; Ormoneit et al., 2005), little work has
been done to employ the multi-linear structure of the
motion data bases or to use the physics-based layer
for the temporal alignment. Whereas some work has
been done on using the physics-based layer (Majkow-
ska et al., 2006; Safonova and Hodgins, 2005) as dis-
tance measures, the only work we are aware of on
using multi-linear models for motion data is (Mukai
and Kuriyama, 2006).
The very successful use of multi-linear models in
the context of facial animation (Vlasic et al., 2005)
has been a major motivation for us to investigate them
in the context of motion capture data.
1.1 Our Contribution
In the following we will show that using naturally
occurring modes in several classes of motion can be
used to efficiently represent the motions in a multi-
linear model.
Using a data base of captured motions in which
several actors performed various motions in different
styles in different interpretations we build multi-mode
representations of various classes of motions:
• For one class of motions the motions have to be
time-aligned and warped.
Whereas in principal any time warping method
could be used for this task, we found it beneficial
to use distance measures involving the physics-
based layer of a motion.
• A higher-order data tensor ∆ is built using differ-
ent modes of the motions.
• Using an higher-order SVD a core tensor Φ can
be computed, which can be used for representing
low-dimensional approximations of the motions.
We investigate the properties of the resulting
multi-mode representation, especially with respect to
21
Krüger B., Tautges J. and Weber A. (2007).
MULTI-MODE REPRESENTATION OF MOTION DATA.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 21-29
DOI: 10.5220/0002079200210029
Copyright
c
SciTePress

dimensionality reduction and its suitability for syn-
thesizing new motions by morphing.
We will show that especially for the approxima-
tions of motions by few components the reduction
based on a multi-linear model can be considerably
better than one obtained by principal component anal-
ysis (PCA).
2 MULTI-LINEAR ALGEBRA
For our tensor operations we use multi-linear algebra
which is an generalization of linear algebra.
A tensor is the basic mathematical object of multi-
linear algebra, it is a generalization of vectors (tensor
1st order) and matrices (tensor 2nd order). A tensor of
nth order can be thought as an n-dimensional block
of data. While within a matrix the two dimensions
(columns and rows) correspond to two modes, a ten-
sor can be build up with more general modes. A more
detailed description of multi-linear algebra is given in
(Vlasic et al., 2005).
2.1 Tensor Construction
There are different natural possibilities to fill the data
tensor ∆ of our multi-mode model. Some do not re-
quire any preprocessing, some require e.g. a temporal
alignment of the motions. In the following we inves-
tigate the use of six different modes:
a) Actor Mode, all motions are captured from dif-
ferent people.
In our example motion data base, the actors were
given the same instructions how to perform the
motions. The five actors performing the motions
all have been healthy young adult male persons.
b) Style Mode, when possible we captured several
styles of the motion classes.
The meaning of style differs for the various mo-
tion classes; we describe them more closely in
section 4.
c) Repetition Mode (Interpretation Mode), all
motions are captured several times.
The instructors were told to stay within the same
verbal description of the motion and its style, but
nevertheless to have some variations in their inter-
pretations of the motion and the style.
These are quite generally applicable modes, they con-
sist of complete motions that span the space of the
considered motion classes.
The following modes are of a more technical na-
ture.
d) Data Mode, all information of a motion is stacked
into a single vector.
e) Frame Mode, this mode space is spanned by the
frames of the captured motions.
f) DOF Mode, all motion degrees of freedom are
separated in this mode. This mode depends on the
representation of the motion data.
They give a description of how the motion data are
arranged for the tensor construction. Either we stack
a complete motion into the Data Mode or the motion
is split into the Frame and DOF Mode. In (Mukai
and Kuriyama, 2006) the authors only focus on joint,
time and motion correlations, hence they are just us-
ing some technical modes.
2.2 Data Tensor
A tensor with the smallest number of modes was cre-
ated by using the natural modes a, b and c. Therefore
the motion data have to be filled into one vector to
construct the data mode. The matrix of size n × f,
which represents one motion, is stacked into one col-
umn. With this arrangement we obtain a tensor in the
size of f · n × a × b × c, where a is the number of ac-
tors in the Personal Mode, b is the size of the different
motion styles used for the Style Mode, c is the num-
ber of motion sequences in the Repetition Mode, f is
the number of frames in the Frame Mode and n is the
number of degrees of freedom for the given motion
representation.
A further tensor of a higher order is constructed
by using the three natural modes and the Frame and
DOF Mode. The result is a data tensor ∆ which has a
size of f × n × a × b × c.
2.3 N -Mode SVD
Similar to (Vlasic et al., 2005), the data tensors ∆
i
can
be transformed by an N -mode singular value decom-
position (N -mode SVD). For this purpose we used the
N-way Toolbox (C. A. Andersson and R. Bro, 2000).
The result is a tensor Φ
0
i
and respective matrices U
i
.
Mathematically this can be expressed in the following
way:
∆
i
= Φ
0
i
×
1
U
i,1
×
2
U
i,2
. . . ×
n
U
i,n
Where ×
n
describes the mode-n product. Mode-n-
multiplying a tensor T with matrix M replaces every
mode-n-vector v of T with a transformed vector M v.
A reduced model Φ
i
can be obtained by truncation
of insignificant components from Φ
0
i
and of matrices
U
i
, respectively. In the special case of a 2-mode ten-
sor this procedure is equivalent to principal compo-
nent analysis (PCA).
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
22

2.4 Motion Reconstruction
Once we have obtained the reduced model Φ
i
and
its associated matrices U
i
, we are able to approx-
imate any original motion. This is done by first
mode-multiplying the core tensor with every matrix
U
i
belonging to a technical mode, and then mode-
multiplying the resulting tensor with one row of every
matrix belonging to a natural mode.
Furthermore, with this model in hand, we can gen-
erate an arbitrary interpolation of original motions by
using linear combinations of rows of U
i
with respect
to the natural modes.
3 TIME WARPING
Dynamic time warping (DTW) algorithms are widely
used in motion data processing to get a temporal
correspondence of the used motions. Such a corre-
spondence is needed to get reasonable realistic results
when synthesizing motions (Bruderlin and Williams,
1995; Giese and Poggio, 2000; Kovar and Gleicher,
2003). The result of a time warp depends on the used
algorithm, the given distance measurement and the
features with which the motions are compared. Until
now mainly kinematic features were used to compare
whole body motions. Dynamic features were only
used in the context of spliced body motions (Majkow-
ska et al., 2006).
3.1 Iterative Multi-scale Dynamic Time
Warping
We use the Iterative Multi-scale Dynamic Time Warp-
ing (IMDTW) algorithm presented by (Zinke and
Mayer, 2006). This enhanced algorithm is used be-
cause it has no quadratic runtime and does not need
quadratic memory space. This goal is reached by
combining two approaches:
• The possible pathes are restricted
• The path is searched iteratively with several reso-
lutions of the cost matrix
This iterative dynamic time warping algorithm works
on windows of the given (maybe high dimensional)
time series. After the first iteration we have got a path
through the low resolution DTW matrix. We use a
tube around this path for the next iteration where we
calculate this tube with a smaller windows size what
results in a higher resolution.
3.2 Distance Measure
Our time warping algorithm is parameterized with the
following distance measure. For every frame i of a
considered motion we build a frame feature vector
f(i). This vector contains all properties of the mo-
tion that should be used for comparison. These frame
feature vectors are put together over a frame window
f(i), . . . , f(i + n) as normalized sum to compute a
feature vector F(i). Now we use the scalar product
of these feature vectors to compute a distance between
two motions:
D(F
1
(i), F
2
(j)) = 1 − hF
1
(i), F
2
(j)i
By this method we can handle a lot of different
features parallel. It is also possible to give a specific
feature a special weight by scaling. This feature then
contributes more to the direction the vector points in.
3.3 Distance Features
We found it very beneficial to include features on the
physics-based level. For this purpose the mass from
all segments of a skeleton and their center of mass
have to be calculated. We use the heuristics based on
anthropometric tables described in (Robbins and Wu,
2003) for this purpose.
In addition to the center of mass (and its acceler-
ation) of the entire body we also use the angular mo-
mentum of the body segments as physics-based fea-
tures for comparing motions. Using a local coordi-
nate system aligned to the motion, these features are
independent of the starting position and orientation of
the root segment. Although this local coordinate sys-
tem strictly speaking is not an inertial system the oc-
curring pseudo-forces are rather negligible for typical
human motions.
All these simple features give a lot of information
on the viewed motions. Based on the acceleration of
the center of mass it is, for example, simple to de-
tect non-contact phases. Then the COM-acceleration
is equivalent to acceleration due to gravity when the
body has no ground contact:
a
COM
≈ a
earth
=
0.0
−9.81
0.0
Figure 1 shows the acceleration of the center of
mass of a dancing motion. There are three non-
contact phases that can be easily detected by analyz-
ing the y-component.
Figure 2 shows two distance matrices produced
by our DTW algorithm when comparing two walk-
ing motions. In dark areas the motions are equal, in
MULTI-MODE REPRESENTATION OF MOTION DATA
23

Figure 1: Accelerations of the center of mass of the entire
body of a dancing motion involving different jumps. One
can see two long non-contact phases corresponding to two
long jumps and one short intermediate non-contact step (ex-
tract from motion 05 16 from CMU mocap data base.)
Figure 2: DTW distance matrices calculated on the base of
different features. Acceleration of the whole body center of
mass (left), acceleration of the whole body center of mass,
hands and feet (right). The best warping paths are drawn
red.
brighter areas the motions are unequal, correspond-
ing to the given features. The red line is the warping
path found by the algorithm. The left one is based
only on the acceleration of the center of mass. In this
checkerboard-like pattern we have thirteen black di-
agonals. This shows that we can not differentiate be-
tween the steps. If we add the acceleration of the feet
to our features, the result gets obviously better. This
can be seen in the right picture of figure 2. There we
have got five dark diagonals, so steps made with the
same foot are detected as similar.
The right matrix is not as symmetric as the left
one. This shows that the motion is not similar to the
same backward motion.
Depending on the motions that should be time
warped, one can select specific features.
For walking motions the movement of the legs
gives the most important features, if the steps should
be synchronized. For Karate-like kicking motions
the foot that makes the kick is most important. The
moments, in the compared motions, where the leg is
stretched have to be matched to each other. There-
fore features from this leg should get a higher weight.
Another example we tested are cartwheel motions. To
get a good correspondence for these motions, features
that describe the motion of hands an feet are useful. A
result of this warping technique for a walking motion
is presented in the video.
4 RESULTS
For our experiments we built our motion model
for three motion classes: walking, grabbing and
cartwheel motions. For all of these motion classes
we constructed data tensors with motion representa-
tion based on Euler angles and based on quaternions.
Initially some preprocessing was required, consisting
mainly of the following steps. All motions were
a) filtered in the quaternion domain with a smooth-
ing filter described in (Lee and Shin, 2002);
b) aligned over time by the time warping using
physics-based distance features;
c) moved to the origin with their root node and ori-
ented to the same direction;
d) finally sampled down to a frame-rate of 30 Hz.
By applying the N-Mode SVD on the data tensors
that were constructed of these motions we got the
core-tensors Φ that were used for the following ex-
periments.
4.1 Walking Motions
For this motion class we used walking motions out
of our database, from five actors which were asked to
perform the following four motions for three times:
• walk four steps in a straight line.
• walk four steps in a half circle to the left side.
• walk four steps in a half circle to the right side.
• walk four steps on the place.
All motions had to start with the right foot. All mo-
tions were aligned over time to the length of the first
motion of actor one. The five actors performing the
motions all have been healthy young adult male per-
sons.
All motions were repeated by all actors for three
times. The actors were asked to stay within the same
verbal description of the motion and its style, but nev-
ertheless to have some variations in their interpreta-
tions of the motion and the style.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
24

Table 1: Dimension, mean errors and size of the core tensor
for walking motions, represented by Euler angles.
Dimension Mean error Entries
Core Tensor walking Core Tensor
motions
(degrees)
Truncated Data Mode
5022 × 5 × 4 × 3 0.0 301320
64 × 5 × 4 × 3 0.0 3840
61 × 5 × 4 × 3 0.0 3660
58 × 5 × 4 × 3 0.1 3480
55 × 5 × 4 × 3 0.3 3300
40 × 5 × 4 × 3 1.3 2400
25 × 5 × 4 × 3 2.6 1500
10 × 5 × 4 × 3 4.4 600
1 × 5 × 4 × 3 7.3 60
Truncated DOF Mode
62 × 81 × 5 × 4 × 3 0.0 301320
52 × 81 × 5 × 4 × 3 0.0 252720
40 × 81 × 5 × 4 × 3 0.2 194400
31 × 81 × 5 × 4 × 3 0.8 150660
22 × 81 × 5 × 4 × 3 1.5 106920
10 × 81 × 5 × 4 × 3 3.8 48600
1 × 81 × 5 × 4 × 3 11.2 4860
Truncated Actor Mode
62 × 81 × 4 × 4 × 3 3.1 241056
62 × 81 × 3 × 4 × 3 5.2 180792
62 × 81 × 2 × 4 × 3 6.8 120528
62 × 81 × 1 × 4 × 3 9.4 60264
Truncated Style Mode
62 × 81 × 5 × 3 × 3 4.0 225990
62 × 81 × 5 × 2 × 3 5.6 150660
62 × 81 × 5 × 1 × 3 7.7 75330
Truncated Repetition Mode
62 × 81 × 5 × 4 × 2 2.1 200880
62 × 81 × 5 × 4 × 1 4.7 100440
4.1.1 Truncating Technical Modes
For our truncation experiments we systematically
truncated a growing number of components of the
core-tensors and reconstructed all motions. The mean
difference between all reconstructed and original mo-
tions – depending on the size of the truncated core-
tensor—is shown in table 1. The considered motions
were warped to a length of 81 frames and our skele-
ton, based on Euler angles, has 62 degrees of free-
dom. On this basis the resulting data tensor has a size
of 5022 × 5 × 4 × 3. The resulting core tensor after
applying an N-Mode SVD was now reduced. In fig-
ure 3 the mean error E over all motions and all frames
is shown graphically in dependence of the size of the
Data Mode (blue). This error is defined as follows:
E = (
Frames
X
i
DOFS
X
j
abs(e
org
i,j
− e
rec
i,j
))/(Frames · DOFS),
Figure 3: Mean error of reconstructed walking (blue), grab-
bing (green) and cartwheel (red) motions, depending on the
size of the Data Mode of the core tensor.
Figure 4: Displacement in degrees for truncated Frame and
DOF Mode.
where Frames is the number of all frames of all mo-
tions that were used to build the data tensor, and
DOFS is the number of degrees of freedom of the
underlying skeleton. This error is always calculated
on Euler angles hence the motions are stored in the
ASF/AMC file format.
One can see that the motions are reconstructed
without any visible error with no more than 61 of the
original 5022 dimensions.
If the technical Data Mode is split up into the
Frame and DOF Mode it is possible to make a sim-
ilar experiment by truncating both modes. The result
is shown in figure 4. If just the DOF Mode is trun-
cated the motion is reconstructed with a mean error
of less than one degree for more than 26 degrees of
freedom. The same displacement can be reached by
reducing the Frame Mode down to a size of 20.
MULTI-MODE REPRESENTATION OF MOTION DATA
25
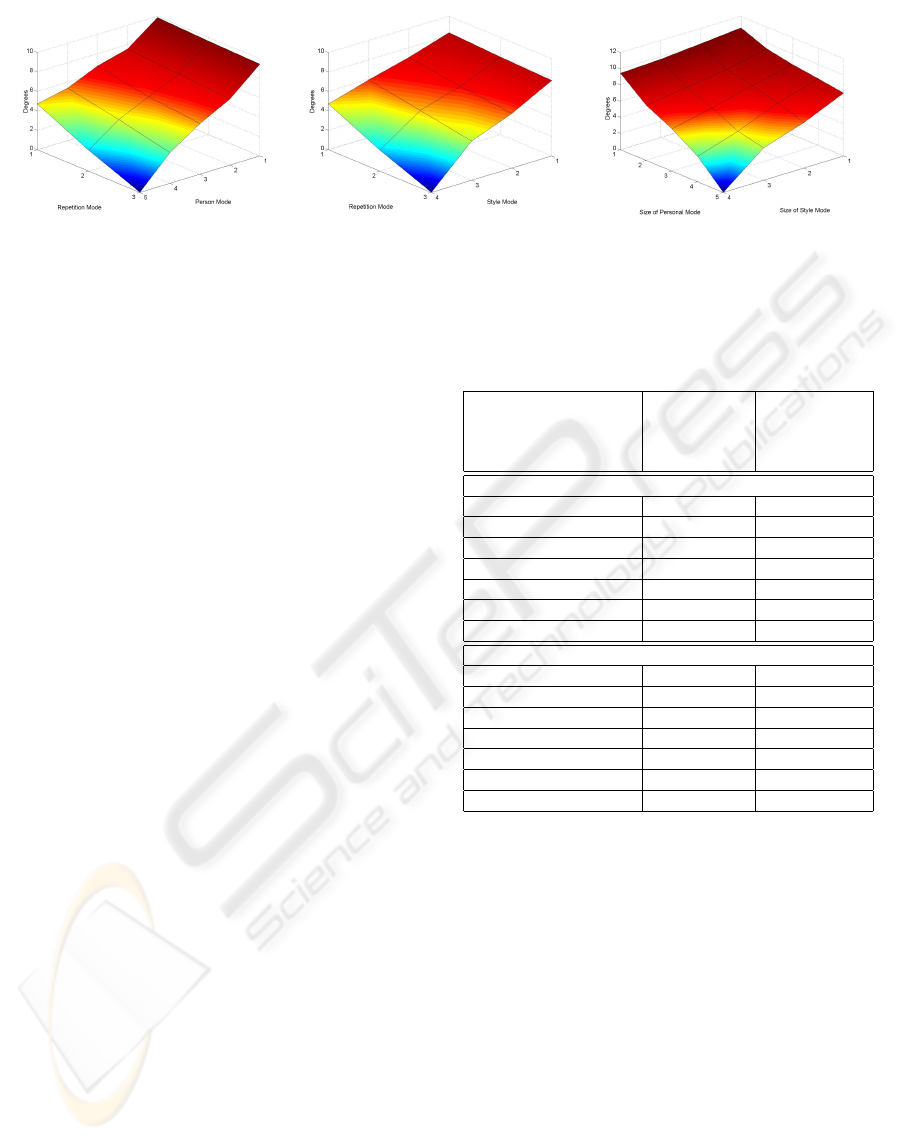
Figure 5: Mean error, in degrees, of reconstructed motions where two natural Modes were truncated. Style and Repetition
Mode are truncated (left). Personal and Repetition Mode are truncated (middle). Style and Personal Mode are truncated
(right).
4.1.2 Truncating Natural Modes
To verify the importance of natural modes we pro-
ceeded in the same way. In fact the displacement is
at the lowest size for the Repetition Mode. This is
what one would expect since the actors were asked to
perform the same action multiple times. The reason
for the observed displacement, is given through the
different interpretations of the motions. Note that sev-
eral interpretations from one actor are giving a smaller
variance, than motions from different actors or mo-
tions in different styles. The results of these experi-
ments are shown in figure 5. The displacement grows
higher with the size of truncated values from Style-
and Personal Mode.
4.2 Grabbing Motions
For this motion class the actors, which have been
the same as for the walking motions, were asked to
perform grabbing motions from a storage rack. The
Style Mode is derived from three different heights
(low, middle, and high). We took three takes of all
motions, that the repetition-mode has a size of three.
All grabbing motions were performed with the right
hand. Again all motions were warped to the length of
one reference motion. The data tensor has a size of
f · dof × 5 × 3 × 3. The resulting error for truncated
components of the Data Mode is shown in figure 3
(green).
4.3 Cartwheel Motions
The last class of motions we considered are cartwheel
motions. We captured several cartwheels from
four persons. All actors were asked to start their
cartwheels with the left foot and the left hand. We did
not define different “styles” for cartwheel motions.
The core tensor had a size of 6138 × 4 × 1 × 3. Here
Table 2: Dimension, mean errors and size of the core tensor
for grabbing motions, represented with Euler angles.
Dimension Mean error Entries
Core Tensor grabbing Core Tensor
motions
(degrees)
Truncated Data Mode
4340 × 5 × 3 × 3 0.0 195300
58 × 5 × 3 × 3 0.0 2610
55 × 5 × 3 × 3 0.0 2475
40 × 5 × 3 × 3 0.6 1800
25 × 5 × 3 × 3 2.4 1500
10 × 5 × 3 × 3 5.1 450
1 × 5 × 3 × 3 8.6 45
Truncated DOF Mode
62 × 70 × 5 × 3 × 3 0.0 195300
52 × 70 × 5 × 3 × 3 0.0 163800
40 × 70 × 5 × 3 × 3 0.3 126000
31 × 70 × 5 × 3 × 3 0.9 97650
22 × 70 × 5 × 3 × 3 1.9 69300
10 × 70 × 5 × 3 × 3 4.4 31500
1 × 70 × 5 × 3 × 3 9.7 3150
all motions could be reconstructed without any visi-
ble error for a size of no more than 34 for the Data
Mode. This results are shown in table 4.3 and can be
seen graphically in figure 3 (red).
4.4 Comparison with PCA
To compare our multi-linear model with linear mod-
els, as they are used for principal component analysis
(PCA), we constructed two tensors for our model and
two matrices for the PCA based on the same motions.
Figure 6 shows a comparison of the results for walk-
ing (left) and grabbing motions (right). The mean er-
ror over all reconstructed motions depending on the
number of principal components and the size of the
DOF Mode is shown in this figure. The mean error for
motions reconstructed from the multi-mode-model is
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
26

Figure 6: Mean error of reconstructed motions with reconstructions based on our model (blue) and based on a PCA (green).
The result is shown for walking motions (left) an d grabbing motions (right).
Table 3: Dimension, mean errors and size of the core tensor
for cartwheel motions, represented by Euler angles.
Dimension Mean error Entries
Core Tensor cartwheel Core Tensor
motions
(degrees)
Truncated Data Mode
6138 × 4 × 1 × 3 0.0 73656
34 × 4 × 1 × 3 0.0 408
31 × 4 × 1 × 3 1.4 372
16 × 4 × 1 × 3 4.4 192
1 × 4 × 1 × 3 11.8 12
smaller than the error from the motions reconstructed
from principal components. Thus a motion can be re-
constructed with a mean error less than one degree
above the complete motion from a core tensor when
the DOF Mode is truncated to just three components.
Thus especially in cases when a motion should be
approximated by rather few components the reduction
based on the multi-linear model is considerably better
than the one done by PCA.
4.5 Motion Synthesis
As it was described in Sect. 2.4, it is possible to syn-
thesize motions with our multi-linear model. For ev-
ery mode i there is an appropriate matrix U
i
, where
every row u
i,j
represents one of the motions j, this
mode consists of. Therefore an inter- or extrapolation
can be done between any rows of U before they are
multiplied with the core tensor Φ to synthesize a mo-
tion. To prevent our results from unrequested effects
like turns and unexpected flips resulting from a repre-
Figure 7: Screenshot from the original motions that are
from the styles walking forward (red) and walking a left
circle (orange), the synthetic motion (yellow) is produced
by a linear combination of these styles.
sentation based on Euler angles we used our quater-
nion based representation to synthesize motions.
For the following walking example we con-
structed a motion that was interpolated between two
different styles. The first style was walking four steps
straight forward and the second one was walking four
steps on a left round. We made a linear interpolation
by multiplying the corresponding rows with the factor
0.5. The result is a four step walking motion that de-
scribes a left round, with a larger radius. One sample
frame of this experiment can be seen in figure 7. An-
other synthetic motion was made by an interpolation
MULTI-MODE REPRESENTATION OF MOTION DATA
27

Figure 8: Screenshot from the original motions that are
from the styles grabbing low (red) and grabbing high (or-
ange), the synthetic motion (yellow) is produced by a linear
combination of these styles.
Figure 9: Screenshot from four original walking motions
and one synthetic motion, that is an result of combining two,
the personal and the style mode. The original motions of
the first actor are on the left side, the original motions of the
second actor are on the right side and the synthetic example
can be seen in the middle.
of grabbing styles. We synthesized a motion by an
interpolation of the styles grabbing low and grabbing
high. The result is a motion that grabs in the mid-
dle. One result of this synthetic motion is shown in
figure 8.
With this technique we are able to make interpo-
lation between all modes parallel. One example is a
walking motion that is an interpolation between the
style and actors Mode. One picture of this result is
given in figure 9.
For more detailed results of our motion synthesis
we refer to the video.
5 CONCLUSION AND FUTURE
WORK
We have shown that exploring naturally occur-
ring modes in motion databases and representing
motions in multi-linear models—after appropriate
preprocessing—is a feasible way to represent mo-
tions of a database allowing different synthesis, anal-
ysis and compression of the motions. We expect that
multi-mode representations will be either an interest-
ing alternative or an additional toolkit in basically all
cases, in which currently principal component analy-
sis is used. As has been shown by our experiments,
the benefit of the multi-linear representation over a
simply linear representation of a suitably structured
collection of motion data is especially relevant if mo-
tions should be approximated by rather few compo-
nents, e.g. in the context of reconstruction of motion
by low-dimensional control signals (Chai and Hod-
gins, 2005) or in the context of auditory presentation
of a motion (Droumeva and Wakkary, 2006; R
¨
ober
and Masuch, 2005; Effenberg et al., 2005). This pa-
per presents a proof of concept, for which we could
use a motion database having examples for all data
of the built tensors. In general one might only have
sparsely given data for the different modes. However,
we presume that techniques similar to the ones used
to fill the data tensors in the case of faces from sparse
data (Vlasic et al., 2005) can be used for motion data,
too. It will be a topic of our future research to inves-
tigate these techniques and to apply the multi-mode
representation to some of the tasks mentioned above.
ACKNOWLEDGEMENTS
We are grateful to Bernd Eberhardt and his group of
Hochschule der Medien in Stuttgart for the possibility
to build a systematic motion capture data base, which
is underlying our empirical investigations. Meinard
M
¨
uller and Tido R
¨
oder have not only been driving
forces behind the idea of building such a data base
but also contributed to its realization in many ways
– from serving as some of the actors to transforming
motion files into a well organized data base of motion
clips.
REFERENCES
Arikan, O. (2006). Compression of motion capture
databases. ACM Trans. Graph., 25(3):890–897. SIG-
GRAPH 2006.
Barbi
ˇ
c, J., Safonova, A., Pan, J.-Y., Faloutsos, C., Hodgins,
J. K., and Pollard, N. S. (2004). Segmenting mo-
tion capture data into distinct behaviors. In Proceed-
ings of the 2004 conference on Graphics interface,
pages 185–194. Canadian Human-Computer Commu-
nications Society.
Bruderlin, A. and Williams, L. (1995). Motion signal pro-
cessing. In Proceedings of the 22nd annual con-
ference on Computer graphics and interactive tech-
niques, pages 97–104. ACM Press.
C. A. Andersson and R. Bro (2000). The N-way Toolbox
for MATLAB. http://www.models.kvl.dk/
source/nwaytoolbox/.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
28

Carnegie Mellon University Graphics Lab (2004). CMU
Motion Capture Database. mocap.cs.cmu.edu.
Chai, J. and Hodgins, J. K. (2005). Performance animation
from low-dimensional contr ol signals. ACM Trans.
Graph., 24(3):686–696. SIGGRAPH 2005.
Droumeva, M. and Wakkary, R. (2006). Sound intensity
gradients in an ambient intelligence audio display. In
CHI ’06 extended abstracts on Human factors in com-
puting systems, pages 724–729, New York, NY, USA.
ACM Press.
Effenberg, A., Melzer, J., Weber, A., and Zinke, A. (2005).
MotionLab Sonify: A framework for the sonification
of human motion data. In Ninth International Confer-
ence on Information Visualisation (IV’05), pages 17–
23, London, UK. IEEE Press.
Giese, M. A. and Poggio, T. (2000). Morphable models for
the analysis and synthesis of complex motion patterns.
International Journal of Computer Vision, 38(1):59–
73.
Glardon, P., Boulic, R., and Thalmann, D. (2004). Pca-
based walking engine using motion capture data. In
CGI ’04: Proceedings of the Computer Graphics In-
ternational (CGI’04), pages 292–298, Washington,
DC, USA. IEEE Computer Society.
Hsu, E., Pulli, K., and Popovi
´
c, J. (2005). Style translation
for human motion. ACM Trans. Graph., 24(3):1082–
1089. SIGGRAPH 2005.
Kovar, L. and Gleicher, M. (2003). Flexible automatic mo-
tion blending with registration curves. In Breen, D.
and Lin, M., editors, Eurographics/SIGGRAPH Sym-
posium on Computer Animation, pages 214–224. Eu-
rographics Association.
Kovar, L. and Gleicher, M. (2004). Automated extraction
and parameterization of motions in large data sets.
ACM Transactions on Graphics, 23(3):559–568. SIG-
GRAPH 2004.
Kovar, L., Gleicher, M., and Pighin, F. (2002). Motion
graphs. ACM Transactions on Graphics, 21(3):473–
482. SIGGRAPH 2002.
Lee, J. and Shin, S. Y. (2002). General construction of time-
domain filters for orientation data. IEEE Transactions
on Visualizatiuon and Computer Graphics, 8(2):119–
128.
Majkowska, A., Zordan, V. B., and Faloutsos, P. (2006).
Automatic splicing for hand and body animations.
In ACM SIGGRAPH / Eurographics Symposium on
Computer Animation, pages 309–316.
Mukai, T. and Kuriyama, S. (2006). Multilinear motion
synthesis using geostatistics. In ACM SIGGRAPH /
Eurographics Symposium on Computer Animation -
Posters and Demos, pages 21–22.
Ormoneit, D., Black, M. J., Hastie, T., and Kjellstr
¨
om,
H. (2005). Representing cyclic human motion us-
ing functional analysis. Image Vision Comput.,
23(14):1264–1276.
Robbins, K. L. and Wu, Q. (2003). Development of a com-
puter tool for anthropometric analyses. In Valafar,
F. and Valafar, H., editors, Proceedings of the Inter-
national Conference on Mathematics and Engineer-
ing Techniques in Medicine and Biological Sciences
(METMBS’03), pages 347–353, Las Vegas, USA.
CSREA Press.
R
¨
ober, N. and Masuch, M. (2005). Playing Audio-only
Games: A compendium of interacting with virtual, au-
ditory Worlds. In Proceedings of Digital Games Re-
search Conference, Vancouver, Canada.
Safonova, A. and Hodgins, J. K. (2005). Analyzing the
physical correctness of interpolated human motion.
In SCA ’05: Proceedings of the 2005 ACM SIG-
GRAPH/Eurographics symposium on Computer ani-
mation, pages 171–180, New York, NY, USA. ACM
Press.
Safonova, A., Hodgins, J. K., and Pollard, N. S. (2004).
Synthesizing physically realistic human motion in
low-dimensional, behavior-specific spaces. ACM
Transactions on Graphics, 23(3):514–521. SIG-
GRAPH 2004.
Troje, N. F. (2002). Decomposing biological motion: A
framework for analysis and synthesis of human gait
patterns. Journal of Vision, 2(5):371–387.
Vlasic, D., Brand, M., Pfister, H., and Popovi
´
c, J. (2005).
Face transfer with multilinear models. ACM Trans.
Graph., 24(3):426–433. SIGGRAPH 2005.
Zinke, A. and Mayer, D. (2006). Iterative multi scale dy-
namic time warping. Technical Report CG-2006-1,
Universit
¨
at Bonn.
MULTI-MODE REPRESENTATION OF MOTION DATA
29
