
A TEXTURE-BASED METRIC EXTENSION FOR
SIMPLIFICATION METHODS
Carlos González, Pascual Castelló and Miguel Chover
Departmento de lenguajes y sistemas informáticos, Universitat Jaume I, Castellón, Spain
Keywords: Simplification methods, texture, error metric, edge collapse.
Abstract: We present an extension of the error metrics used in the simplification methods based on edge collapse
operations, which takes into account texture information. Many simplification methods are just based on the
geometry of the models, without considering texture information. As a result, the simplified models present
highly distorted textures. The metric presented here avoids the early collapse of edges that collide with non-
uniform regions of the texture. Detection of these regions is performed by an edge detector method based on
Canny. To test the new error metric, a geometric simplification method of our own based on edge collapses
was used. It can be observed that simplified models that are generated with this new metric present more
realistic results than before. This metric modifies the order of the edge collapses and is very useful for
multiresolution models. The computational cost of this metric is negligible in comparison to the
simplification time.
1 INTRODUCTION
Simplification methods were a great step forward in
interactive applications. These methods allow to
avoid storing and processing all the geometry of the
objects in the scene by simplifying them to produce
other objects with less geometry. This reduces the
load on the GPU. These methods attempt to produce
realistic simplified objects, with a similar
appearance to the original one.
Many simplification methods are based solely on
the geometry of the objects and attempt to achieve
good geometric results in the simplified object by,
for example, criteria based on the coplanarity of the
polygons. But in recent years, methods based on the
user’s point of view have been developed. These
methods try to generate not only good geometric
results, but also realistic results for the viewer by
removing, for example, parts of the object that are
not visible to the user. These methods usually work
by rendering the object from several points of view,
that is, by situating the camera at more than one
point around the object. Generally, this distribution
of the cameras is uniform.
But not only final geometry is important in the
output objects. Models usually have additional
attributes to their geometry. Interactive applications,
like games or CAD programs, need to present the
simplified models with a good appearance. These
applications must therefore present well-textured
models in the scene, because textures play an
important role in this kind of application.
There are not many simplification methods that
take texture information into account in the error
metric. As a result, texture is not considered when
calculating the order in which the edges are
collapsed.
One solution to this problem is presented in this
paper. Our work is valid for any simplification
method based on edge collapses.
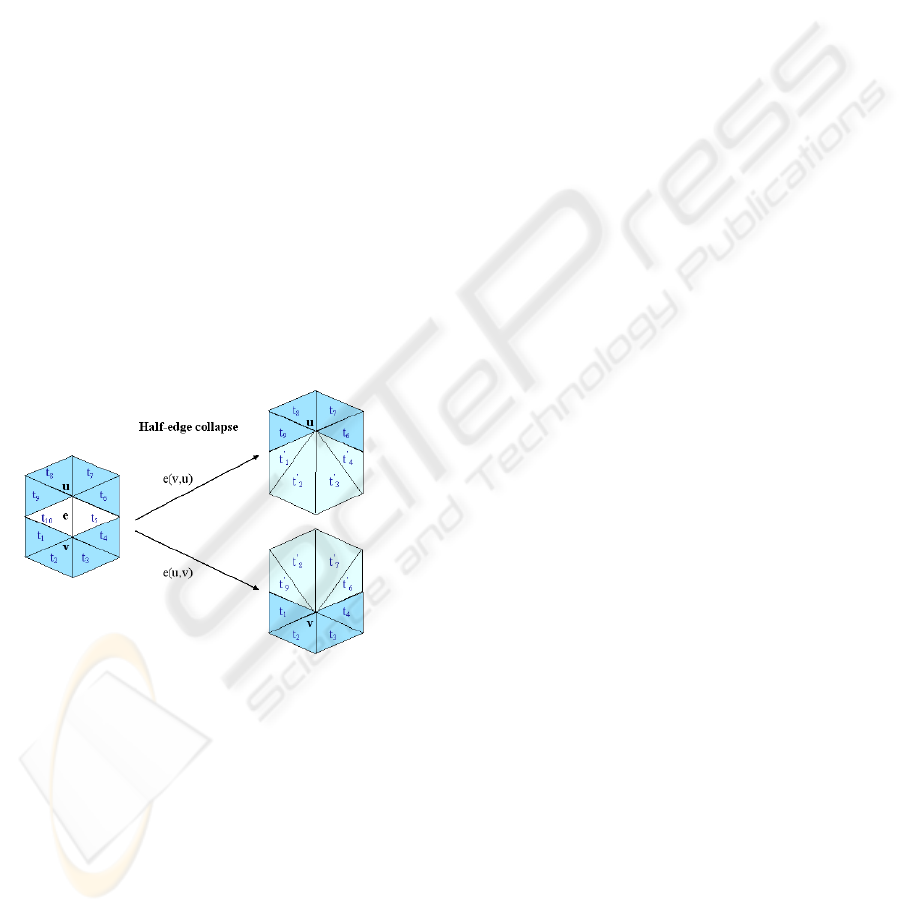
An edge collapse is a simplification operation
that removes edges by merging the vertices of the
edges. The final vertex can be placed at one of the
original vertices (half-edge collapse) or can be
moved to other spatial coordinates. Figure 1 shows
an example of a half-edge collapse operation.
We have developed an extension to the error
metric of any simplification method based on edge
collapses. The error metric extension presented here
is based on the information given by the texture
image. It attempts to distinguish the borders in the
texture and then uses this information to modify the
order of the collapses.
This error metric extension was tested with our
own geometric simplification method based on edge
collapse operations that make use of quadrics. This
69
González C., Castelló P. and Chover M. (2007).
A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 69-76
DOI: 10.5220/0002081000690076
Copyright
c
SciTePress
method did not originally take into account textured
models. Thus, simplifying a model usually produced
an important amount of distortion in the texture. In
an attempt to improve these results, we extended the
method with the error metric presented in this paper
in order to preserve the textures. This metric
produces a later simplification of the regions of the
model that contain abrupt changes in the texture.
This extension is very useful for the generation
of simplification sequences in multiresolution
models, commonly used in games. Multiresolution
models can be rendered in the scene at different
levels of detail, depending on various factors such as
the distance from the object to the viewer, the
relative importance of the object in the scene, etc.
Moreover, this method does not have to store new
texture coordinates at each step of simplification.
Methods that recalculate the texture coordinates,
however, do have to store the new values for each
step, needing more memory for these values.
The rest of this paper is structured as follows. In
Chapter 2 we describe the background to this
research. In Chapter 3 we define the new metric and
a justification of this metric is exposed. Chapter 4
shows some results and in Chapter 5 we discuss the
conclusions.
Figure 1: The half-edge collapse operation. In this
example the edge e is collapsed into vertex u (see e(v, u)),
but is also collapsed into v (see e(u, v)). Triangles t10 and
t5 are removed.
2 PREVIOUS WORK
Cohen et al. (Cohen, Olano & Manocha, 1998)
presented a method that parameterises the model in
order to obtain the texels, obtaining some patches of
the surface. Texture deviation metric is used to
calculate the cost of the pairs. At each simplification
step this metric is calculated for the modified faces.
It also preserves the boundaries.
Garland and Heckbert (Garland & Herbert,
1998) improved their method (Garland & Herbert,
1997) by extending the quadrics, taking into account
the properties of the model. It also preserves the
boundaries, a high collapse cost being assigned to
these edges.
Hoppe (Hoppe, 1999) introduced a new quadric
metric for simplifying meshes while taking attributes
into consideration.
Lindstrom and Turk (Lindstrom & Turk, 2000)
introduced a pure image-based metric. This metric
was used in their image-driven simplification
method. The main advantage of this image metric is
that it allows the texture attributes to be taken into
account, while also measuring the error made in
edge collapse.
Luebke and Hallen (Luebke & Hallen, 2001)
presented a method for performing a view-
dependent polygonal simplification using perceptual
metrics. These metrics derive from a measure of
low-level perceptibility of visual stimuli in humans.
Later Williams et al. (Williams, Luebke, Cohen,
Kelley & Schubert, 2003) extended this work for lit
and textured meshes.
Sander et al. presented a method (Sander et al,
2001) that extended the work introduced in (Hoppe,
1996). This method subdivides the surface into
patches, on the grounds of its coplanarity. It then
generates a parameterisation by minimising the
stretch deviation. It calculates an adequate size for
each object in the texture domain and simplifies the
mesh by minimising the texture deviation (Cohen,
Olano & Manocha, 1998) and preserving the
boundaries. Finally, it optimises the parameterisation
with a different objective function and regroups all
the patches again.
Zhang et al. (Zhang & Turk, 2002) proposed a
new algorithm that takes visibility into account.
Their approach defined a visibility function between
the surfaces of a model and a surrounding sphere of
cameras. The number of cameras increases both
accuracy and calculation time. They used up to 258
cameras. In order to guide the simplification process,
they combined their visibility measure with the
quadric measure introduced by Garland et al.
(Garland & Herbert, 1997).
Lee et al. (Lee, Varshney & Jacobs, 2005)
introduced the idea of mesh saliency as a measure of
regional importance for graphics meshes. This
measure was incorporated into mesh simplification.
Basically, their approach consists in generating a
saliency map and then simplifying by using this map
in the QSlim algorithm as in (Zhang & Turk, 2002).
The new edge collapse cost is that of the quadric
multiplied by the saliency of this edge.
Garland and Zhou (Garland & Zhou, 2005)
presented a method for simplifying simplicial
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
70

complexes of any type embedded in Euclidean
spaces of any dimension.
Both the geometry of the object and also the
texture frequencies were considered in (Xu, Sun &
Xu, 2005). To make the method more precise, pixels
are subdivided into subpixels.
The method presented in (Chen & Chuang,
2006) recalculates a new texture for each
simplification step, an indexing map being used to
avoid loss of precision.
3 ERROR METRIC EXTENSION
FOR TEXTURED MODELS
It is very important to use a simplification that
produces well-textured simplified objects, because
of the visual importance of texture.
There are many simplification methods for tri-
dimensional models, but only a few of them consider
the texture information in its error metric (Garland
& Herbert, 1998) (Hoppe, 1999) (Xu, Sun & Xu,
2005). Therefore, the methods which do not consider
texture information usually present simplified
models with distorted textures. The methods which
do consider this information normally use a specific
metric that is only valid for them.
Our error metric extension is very useful for
multiresolution methods because it does not need to
store new values for each level of detail. We
distinguish between our technique and the methods
that recalculate the values of the texture coordinates
at each level of detail.
In this paper we present a solution to this
problem. Thus, the error metric extension presented
here provides a way to consider the texture
information in methods in which no texture
information is taken into account in the metric.
3.1 Error Metric Extension
We have developed a new texture-based error metric
extension for simplification algorithms which use
the edge collapse operation. It is based on the shape
of the texture, so that the simplified model has a
more realistic appearance when the texture is
applied. Simplification methods which use edge
collapses assign a cost to each edge that determines
the order of the collapses. Depending on the borders
of the texture, we modify the cost of each edge in
order to penalise those edges that intersect these
borders. We will now go on to explain the steps
performed in order to achieve this.
First of all we detect the borders of the texture.
This is performed by an edge detector method based
on Canny (Canny, 1983) (Canny, 1986). This edge
detector works in a multi-stage process. First, a
Gaussian convolution is applied in order to smooth
the texture. Then, regions of the texture with high
first spatial derivatives are highlighted by applying a
simple 2D first derivative operator. Edges give rise
to ridges in the gradient magnitude image. Non-
maximal-suppression is then applied, that is, all
pixels that are not actually on the ridge top are set to
zero. These pixels would be drawn as a thin line in
the output. Two thresholds are used to apply
hysteresis so as to allow the continuity of noisy
edges.
The algorithm has various parameters which
affect the quantity and thickness of output borders.
These parameters are:
• The size of the Gaussian filter: depending on
how much the texture is smoothed by the Gaussian
convolution, less clear lines would be marked as
borders or not.
• Thresholds: the low and high thresholds would
give the algorithm what we think is relevant
information and withhold that which we believe is
not significant.
Once edge detection has been performed, the
result is an image with these borders. The values
(white or black) of each pixel in this image are
stored in a matrix. We now have the shape of the
borders in a data structure and we can work with
them.
If we applied this image to the 3D model, we
could see which edges intersect with borders (see
Figure 2). So, if an edge that intersects any of these
borders is collapsed, a great distortion in the texture
would be obtained. Therefore, these edges must have
a high cost of collapse.
We have to know which edges cross any
particular border. In order to achieve this, we use the
texels of each edge of the model. As a result, we
now know how each edge is located in the texture.
With a few simple 2D operations we can determine
whether this edge rendered in the texture crosses a
border. Let E be the set of these affected edges.
Figure 2 shows the Sphere model textured. In this
model the edges that have a part in a black region
and another part in a white region would pertain to
E.
We store all the active edges in a heap, where
each edge has an associated cost. Therefore, edges
with a lower cost will be collapsed first. We then
modify the previous costs of the edges that pertain to
E to be collapsed later (Figure 3).
A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS
71

The relative area of a region of the model is the
area of this region divided into the sum of the areas
of all the triangles of the model. The previous cost of
each edge is added to the relative area of the
triangles that contain the edge that we are analysing.
Hence, we define the total area of the model as
the sum of the areas of all the triangles in the model
(1). Thus, for one specific edge the additional cost
will be the sum of the areas of the triangles which
contain this edge divided by the total area of the
model (2). The area of each triangle therefore plays
an important role in the order of the edge collapses,
because this factor causes triangles with lower areas
to be removed before triangles with similar previous
costs and higher areas (if the model is manifold, in
an edge collapse one or two triangles are removed).
Therefore, the cost for each edge e of E (c
F
) is
performed as follows:
∑
=
=
n
i
iT
aA
1
(1)
n being the number of triangles in the model and
a
i
the actual area of the triangle i.
T
t
i
i
eF
A
a
cc
∑
=
+=
1
(2)
t being the number of triangles the edge contains
and c
e
is the previous cost of the edge.
Figure 2: Sphere model.
Function getE(Texture, Model)
Begin
E = Ø
M = EdgeDetection(Texture)
For (each e of the Model)
If e collides with a border of M
then
Insert(e, E)
End If
Return E
End
Function computeTextureError(e, E)
Begin
If (e Є E) then
t = getTriangles(e)
Ct = relativeArea(t)
Else
Ct = 0
End If
Return Ct
End
Function computeEdgeCost(e, E)
Begin
Ce = computeEdgeCollapseError(e)
Ct = computeTextureError(e, E)
Return Ce+Ct
End
Figure 3: Pseudo-code for computing the cost of an edge.
Function getE(Texture, Model) returns the set of the edges
that intersect with any border of the texture. It is called at
the beginning of the process. The cost of each edge is
given by the function computeEdgeCost(e, E).
ComputeEdgeCollapseError returns the cost of collapsing
the edge e without considering texture information.
3.2 Justification of the Metric
The method is based on texture information and it is
clear which edges have to be penalised, but we have
to know how to change their collapse cost. We have
chosen the relative area of the triangles that contain
the collapsed edge as error extension, because the
greater the area of a triangle is, the more noticeable
its removal will be in the simplified object.
Another error metric extension that we
considered was the relative area of these triangles in
the texture domain because in this metric we are
taking into account the texture information, but the
texture coordinates of an object may not be
uniformly distributed. Small triangles in the 3D
space may therefore be parameterised with a large
triangle in the texture domain.
An example is shown in Figure 4, where the eye
of the Ninja model is almost as large as the other
parts of the body. If the area of the triangles in the
texture domain were used as the error metric the
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
72

edges that contain the eyes would have a high
collapse cost. But the eyes are relatively small with
respect to other parts of the object when it is
rendered.
Figure 4: Texture of the Ninja Model.
4 RESULTS
Several models have been tested with the new error
metric and it can be observed that the texture in the
simplified models is more accurate to the original
models than in the simplified models without
applying our error metric.
The number of edges in the simplified models
remains unaltered, but the order of the simplification
of these edges was different. Now the edges that
collide in the texture domain with any border
obtained by the edge detector method have a higher
error cost. Thus, those parts of the model that have
fewer edges colliding with borders are more
simplified than before.
The border detection process is performed as a
pre-process. The border detection time depends on
the resolution of the texture and is a very fast
process. Moreover, the computational cost achieved
by this metric at each simplification step is
negligible compared with the simplification time.
The models were simplified by our own
geometric simplification method based on edge
collapse operations. We have tested several
parameters for the edge detector method and we
have chosen those that return what we think are
relevant borders. But if other values were given to
these parameters we would obtain more or fewer
borders of the texture and, consequently, more or
fewer edges that have to be reordered in the collapse
order.
Below, some simplified models are depicted.
Figure 5 shows the original Eye model. In Figure 6
the texture of this model and the borders of this
texture can be seen. Figures 7 and 8 show the
difference between applying and not applying the
metric in the Eye model. Three levels of
simplification are given (75%, 50% and 25%). These
percentages represent the number of edges
untouched. Figure 9 shows the texture of the Ninja
model and its borders detected by the edge detector
method. Figures 10 and 11 show a 50%
simplification of this model without applying the
new metric and applying it. First the original model
is shown (left), then the simplified model without
applying the metric (centre) and finally the
simplified model applying the metric (right). In
Figure 12 the texture of the Robot model and its
borders are shown. Figures 13 and 14 show the
difference between applying the metric with the
Robot model and not applying it in a simplification
at 50%. Figure 15 shows the texture of the
Toonturtle model and the borders that are obtained.
Figures 16 and 17 show a simplification at 25% of
the geometry of the Toonturtle model without
applying the new metric and then applying it. Table
1 shows the number of polygons in each of these
models.
Table 1: Number of polygons in each model.
Model Number of polygons
Eye 5,400
Ninja 1,008
Robot 308
Toonturtle 640
Figure 5: The original Eye model.
A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS
73

Figure 8: Eye model simplified at 75% (left), 50% (centre)
and 25% (right) applying our texture-based error metric.
Figure 6: Borders of the Eye model detected by the edge
detector method with sigma = 0.75, low threshold= 0.5
and high threshold = 0.6.
Figure 7: Eye model simplified at 75% (left), 50% (centre)
and 25% (right) without applying our texture-based erro
r
metric.
Figure 9: Borders of the Ninja model detected by the edge
detector method with sigma = 0.75, low threshold= 0.5
and high threshold = 0.6.
Figure 10: Front of the Ninja model. Original model (left)
and the model simplified at 50% without applying ou
r
texture-based error metric (centre) and applying it (right).
Figure 11: Back of the Ninja model. Original model (left)
and the model simplified at 50% without applying ou
r
texture-based error metric (centre) and applying it (right).
Figure 12: Borders of the Robot model detected by the
edge detector method with sigma = 0.75, low threshold =
0.5 and high threshold = 0.6.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
74

5 CONCLUSIONS
A texture-based error metric extension for
simplification methods that uses edge collapse
operations has been presented. With this extension,
the simplification also considers the texture
information of textured models. It extends the error
metric of any simplification algorithm based on edge
collapses. Thus, the original error and the new error
based on texture information are both used in the
weighting of the edges.
When extending the previous error with this
metric, the simplification order of the regions that
previously had a similar collapse cost may change.
After applying the metric, edge collapses would be
produced earlier in the regions with fewer changes
in the texture. Thus, the regions with great changes
in the texture are simplified later than the others that
have fewer changes in the texture and a similar
previous error. This method therefore avoids the
early simplification of triangles which contain
abrupt changes in the texture, which prevents great
texture distortions from appearing in simplified
models.
In consequence, this method is very useful for
multiresolution models, because it does not have to
store new texture coordinates at each step.
Figure 16: Front of Toonturtle model. Original model
(left) and the model simplified at 25% without applying
our texture-
b
ased error metric (centre) and applying it
(right).
Figure 17: Back of Toonturtle model. Original model (left)
and the model simplified at 25% without applying ou
r
texture-based error metric (centre) and applying it (right).
Figure 13: Front of Robot model. Original model (left) and
the model simplified at 50% without applying our texture-
based error metric (centre) and applying it (right).
Figure 14: Back of Robot model. Original model (left) an
d
the model simplified at 50% without applying our texture-
based error metric (centre) and applying it (right).
Figure 15: Borders of the Toonturtle model detected by
the edge detector method with sigma = 0.75, low
threshold= 0.5 and high threshold = 0.6.
A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS
75

The computational cost introduced by this metric
is negligible in comparison to the simplification
cost.
Thus, this paper presents a way of extending the
error metric of the simplification methods in order to
take the textures into account.
ACKNOWLEDGEMENTS
This work has been supported by the Spanish
Ministry of Education and Science (MATER project
- TIN2004-07451-C03-03, TIN2005-08863-C03-
03), the European Union (GAMETOOLS project
IST-2-004363), the Jaume I University
(PREDOC/2005/12) and FEDER funds.
REFERENCES
Canny., J. (1983). A variational approach to edge
detection. In AAAI-83.
Canny, J. F. (1986). A computational approach to edge
detection. IEEE Trans. Pattern Analysis and Machine
Intelligence, 679-698.
Chen, C.-C., Chuang, J.-H. (2006). Texture Adaptation for
Progressive Meshes. Eurographics06-Geometry
Compression and Decompression.
Cohen, J., Olano, M., Manocha, D. (1998). Appearance-
Preserving Simplification. Proceedings of ACM.
SIGGRAPH 98. 115-122.
Garland, M., Heckbert, P. S. (1997) Surface Simplification
Using Quadric Error Metrics. Computer Graphics
(SIGGRAPH 97 Proceedings), 209-218.
Garland, M., Heckbert, P. S. (1998). Simplifying Surfaces
with Color and Texture Using Quadric Error Metrics.
Ninth IEEE Visualization 1998 (VIS'98), 264.
Garland, M., Zhou, Y. (2005, April) Quadric-based
Simplification in any Dimension. ACM Transactions
on Graphics, 24(2). Draft preprint available as Tech
Report UIUCDCS-R-2004-2450.
Hoppe, H. (1996). Progressive Meshes. Computer
Graphics (Proc. Siggraph 96), vol. 30, ACM Press,
New York, pp. 99-108.
Hoppe, H. (1999) New Quadric Metric for Simplifying
Meshes with Appearance Attributes, Proc. IEEE
Visualization 99, IEEE CS Press, Los Alamitos, Calif.,
pp. 59-66.
Lee C.H., Varshney A., Jacobs D.W. (2005). Mesh
saliency. ACM Trans. Graph. 24, 3, pp. 659-666.
Lindstrom P., Turk G. (2000, July). Image-driven
simplification. ACM TOG 19, 3, 204-241.
Luebke D.P., Hallen B. (2001) Perceptually-driven
simplification for interactive rendering. Proc. of the
12th Eurographics Workshop on Rendering
Techniques (London, UK), 223-234.
Sander, P., Snyder, J. Gortler, S., Hoppe, H.
(2001).Texture mapping progressive meshes. Proc.
SIGGRAPH, 409-416.
Williams N., Luebke D., Cohen J.D., Kelley M., Schubert
B. (2003). Perceptually guided simplification of lit,
textured meshes. Proc. of the 2003 symposium on
Interactive 3D graphics (New York, NY, USA), ACM
Press, 113-121.
Xu, A., Sun, S., Xu, K. (2005). Texture Information
Driven Triangle Mesh Simplification. Computer
Graphics and Imaging.
Zhang E., Turk G. (2002, November). Visibility-guided
simplification. Proc. of IEEE Visualization 2002,
vol.31, pp. 267-274.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
76
