
PREDICTIVE-SPECTRAL COMPRESSION OF
DYNAMIC 3D MESHES
Rachida Amjoun and Wolfgang Straßer
WSI-GRIS, University of Tuebingen, Germany
Keywords: Animation, animated mesh compression, clustering, local coordinate frame, predictive coding, DCT.
Abstract:
This paper proposes a new compression algorithm for dynamic 3d meshes. In such a sequence of meshes,
neighboring vertices have a strong tendency to behave similarly and the degree of dependencies between their
locations in two successive frames is very large which can be efficiently exploited using a combination of Pre-
dictive and DCT coders (PDCT). Our strategy gathers mesh vertices of similar motions into clusters, establish
a local coordinate frame (LCF) for each cluster and encodes frame by frame and each cluster separately. The
vertices of each cluster have small variation over a time relative to the LCF. Therefore, the location of each
new vertex is well predicted from its location in the previous frame relative to the LCF of its cluster. The dif-
ference between the original and the predicted local coordinates are then transformed into frequency domain
using DCT. The resulting DCT coefficients are quantized and compressed with entropy coding. The original
sequence of meshes can be reconstructed from only a few non-zero DCT coefficients without significant loss
in visual quality. Experimental results show that our strategy outperforms or comes close to other coders.
1 INTRODUCTION
Animated objects are frequently used in e-commerce,
education and movies and are the core of video
games. The animation in these applications can be
either generated using motion capturing systems or
simulated by sophisticated software tools like Maya
and Max 3D.
The most common representation of animated
three dimensional objects is the triangle mesh which
consists of the geometric information describing ver-
tex positions and connectivity information describ-
ing how these vertices are connected. 3D animation
consists then of a sequence of consecutive triangle
meshes.
As animation becomes more realistic and more
complex, the corresponding frame meshes become
bigger and bigger, consuming more and more space.
It is therefore indispensable to compress the anima-
tion datasets. Key-frame animation is one of the most
famous and dominant animation representations used
in the industry to represent the animation compactly.
A set of key frames are chosen to describe certain im-
portant key poses in the animation sequence at certain
times. Then all frames in between are generated us-
ing interpolation techniques. For such applications,
even the number of key-frames can be very large, re-
quiring a large memory space and need for effective
compression techniques.
The current coders are dedicated to compress the
triangular meshes of fixed connectivity so that the
connectivity needs to be encoded, stored or transmit-
ted once, then the geometry coding comes into play.
There are several criteria by which developed cod-
ing techniques can be distinguished. One of these cri-
teria is if the approach considers the entire sequence
where the coherency is globally exploited by using
the principal component analysis (PCA) transform or
frame by frame where the coherency is locally ex-
ploited by using for example predictive coding.
In PCA based coding, the global linear behavior
of the vertices through all frames is approximated in
terms of linear space. The animation sequence can
be reduced to a few principal components and coef-
ficients. The efficiency of this technique increases
when the datasets are segmented or clustered, so that
30
Amjoun R. and Straßer W. (2007).
PREDICTIVE-SPECTRAL COMPRESSION OF DYNAMIC 3D MESHES.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 30-38
DOI: 10.5220/0002081200300038
Copyright
c
SciTePress

each group is individually encoded by PCA. This type
of method supports progressive transmission. The
drawback of this approach is it is computationally ex-
pensive.
In predictive methods, for each frame, the differ-
ence between the predicted and the current locations
is encoded with very few bits. These approaches are
simple, not expensive, lossless and well suited for
real-time applications. The drawback of these meth-
ods is that they don’t support progressive transmis-
sion.
Affine transformations well approximate the be-
havior of sets of vertices relative to the initial posi-
tion (the first frame, eventually the I-frame). This
type of method is very effective for animations based
on motion capturing, if the mesh is well partitioned
into almost rigid parts, since the vertices are attached
to the bones and move according to their represen-
tative joints. Therefore, exploiting the coherence in
this animation and finding the transformation that best
matches each group of vertices is easier than finding
a transformation that approximates each part in de-
formed meshes (like a cow animation). The draw-
back of this technique is that it can be computation-
ally expensive depending on the splitting process or
the affine transformation optimization.
In this paper, we propose a new compression algo-
rithm based on predictive and DCT transform in the
local coordinate systems.
The method is inspired from video coding. We
first split the animated mesh into severalclusters (sim-
ilar to macroblocks in video coding) using a simple
and efficient clustering process (Amjoun and Strasser,
2006). Then, we perform a prediction in the local co-
ordinate systems. Finally, we transform the resulting
delta vectors (between the predicted and the original
vertex locations) of each cluster in each frame into the
frequency domain using Discrete Cosine Transform.
2 STATE-OF-ART
During the last decade, extensive research has been
done on static mesh compression, producing a large
number of schemes (see, e.g., (Rossignac, 2004)
or (Alliez and Gotsman, 2005) for comprehensive
surveys of the developed techniques). While re-
search still focuses on efficient compression for huge
static meshes (Isenburg and Gumhold, 2003) ani-
mated meshes have become more and more important
and useful every where. However, the current tech-
niques for the compression of sequences of meshes
independently are inefficient.
Lengyel (Lengyel, 1999) suggested the decom-
posing of the mesh into submeshes whose motions
are described by rigid body transformations. The
compression was achieved by encoding the base sub-
meshes, the parameters of the rigid body transforma-
tions, and the differences between the original and the
estimated locations. Zhang et al. (Zhang and Owen,
2004) used an octree to spatially cluster the vertices
and to represent their motion from the previous frame
to the current frame with a very few number of motion
vectors. The algorithm predicts the motion of the ver-
tices enclosed in each cell by tri-linear interpolation
in the form of weighted sum of eight motion vectors
associated with the cell corners. The octree approach
is later used by K. Mueller et al. (Muller et al., 2005)
to cluster the difference vectors between the predicted
and the original positions. Very recently, Mamou et
al. (Mamou et al., 2006) proposed skinning based rep-
resentation. In their algorithm, the mesh is also par-
titioned, then each submesh in each frame is associ-
ated an affine motion and each vertex is estimated as a
weighted linear combination of the clusters motions.
Finally, the prediction errors are compressed using a
temporal DCT coding.
In prediction techniques, assuming that the con-
nectivity of the meshes doesn’t change, the neigh-
borhood in the current and previous frame(s) of the
compressed vertex is exploited to predict its loca-
tion or its displacement (J.H. et al., 2002; Ibarria
and Rossignac, 2003). The residuals are compressed
up to a user-defined error. For example, Ibarria and
Rossignac (Ibarria and Rossignac, 2003) extended the
parallelogramprediction used in static mesh compres-
sion to animation case and introduced two predictors:
Extended Lorenzo Predictor, a perfect predictor for
translations, and Replica Predictor, which is capa-
ble of perfectly predicting the location of the vertices
undergoing any combinations of translation, rotation,
and uniform scaling.
In PCA based approaches, Alexa et al. (Alexa and
M¨uller, 2000) used PCA to achieve a compact repre-
sentation of animation sequences. Later, this method
is improved by Karni and Gotsman (Karni and Gots-
man, 2004), by applying second-order Linear Pre-
diction Coding (LPC) to the PCA coefficients such
that the large temporal coherence present in the se-
quence is further exploited. Sattler et al. (Sattler et al.,
2005) proposed a compression scheme that is based
on clustered PCA. The mesh is segmented into mean-
ingful clusters which are then compressed indepen-
dently using a few PCA components only. Amjoun
et al. (Amjoun et al., 2006) suggest the use of local
coordinates rather the world coordinates in the local
PCA based compression. They showed that the local
coordinate systems are more compressable with PCA
PREDICTIVE-SPECTRAL COMPRESSION OF DYNAMIC 3D MESHES
31
than the world coordinates.
Guskov et al. (Guskov and Khodakovsky, 2004)
used wavelets for a multiresolution analysis and ex-
ploited the parametric coherence in animated se-
quences. The wavelet detail coefficients are progres-
sively encoded. Payan et al. (Payan and Antonini,
2005) introduced the lifting scheme to exploit the
temporal coherence. The wavelet coefficients are
thereby optimally quantized. Briceno et al (Briceno
et al., 2003) transform the mesh sequences into ge-
ometry images which are then compressed using stan-
dard video compression.
3 OVERVIEW
The local coordinate system has an important prop-
erty that can be very useful for compression of ani-
mation. It exhibits a large clustering over time and the
locations of the vertex tend to form a cluster around
one position (over all frames). Regardless what kind
of deformation the vertices undergo, i.e. rotation, or
translation or scaling or combination of all three rela-
tions, the vertices will generally keep their positions,
at least between two successive frames.
Our technique uses this property to guide the clus-
tering process and to perform a predictive coder.
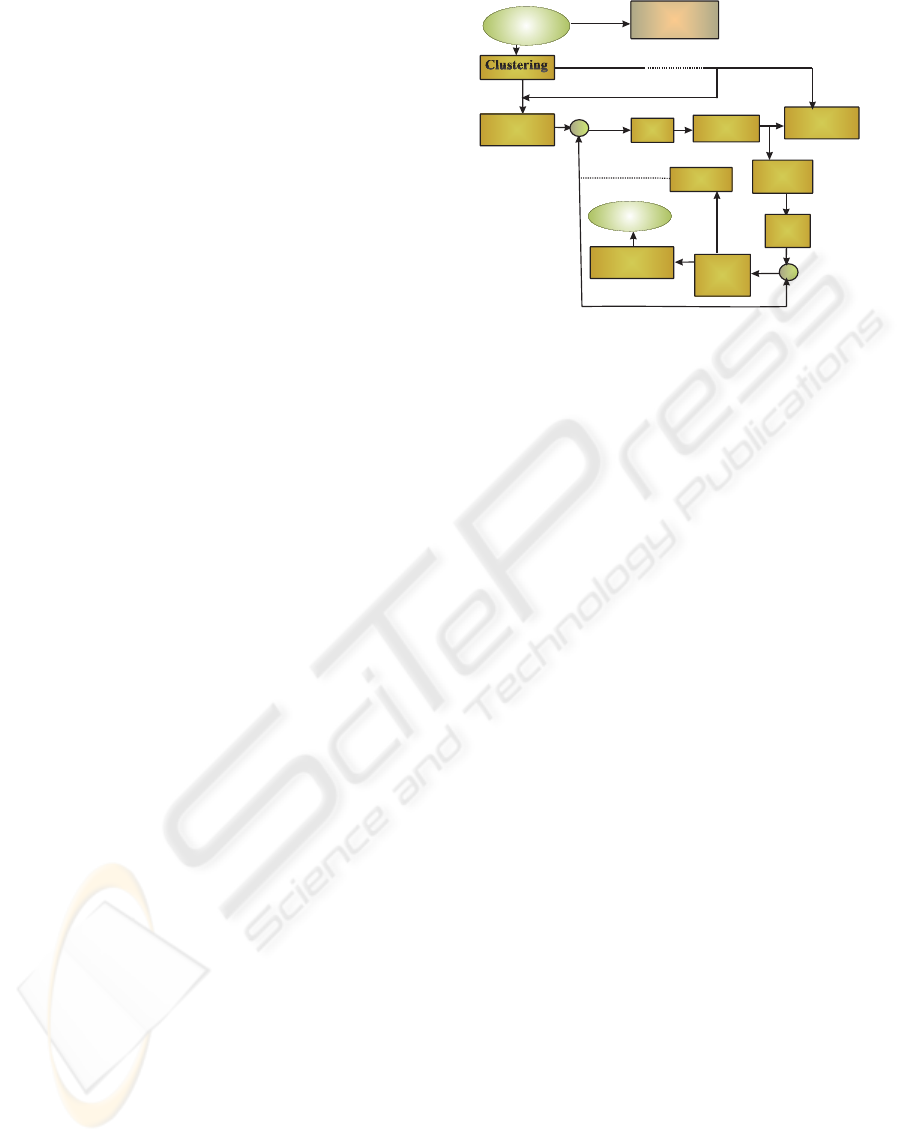
Basically, our algorithm consist of four steps:
1. Clustering process: The vertices are clustered
into a given number of clusters depending on their
motion in the LCFs. Indeed, the vertex should be-
long to the cluster where its deviation in the LCF
through all frames is very small compared to the
other LCFs. Thereby, the efficiency of the predic-
tion through a time increases. Moreover, the clus-
tering will preserve the global shape when DCT
coding is performed (spatially) in each cluster.
2. Lossless coding of LCFs: The locations of the
vertices that contribute to the construction of the
LCF of each cluster should be losslessly encoded.
In order to ensure that the decoder could use the
same LCF, we decode and reconstruct the LCF to
be used during the compression of the remaining
vertices.
3. Predictive coding: This step allows the reduc-
tion of space-time redundancy. It is performed on
the local coordinates rather than the world coor-
dinates, which makes the coding more efficient.
It allows the prediction errors to tend to be very
small. The powerfulness of the predictor strongly
relies on the clustering process. If the vertex is as-
sociated with a LCF whose motion is not similar
to its motion then the local coordinates of the ver-
t
M
¢
~
()
tC
'
i
( )
t
i
d
~
-
+
( )
t
i
d
+
+
Arithmetic
Coder
Inv.
Quant.
Quant.
DCT
DifferentialCodingofLCFs
Reconstr.OfLCFs
Inv.
DCT
( )
tC
'
i
~
1t
M
-
¢
~
Clusters
collect.
Memory
Transf. To
WorldSpac
e
t
t
M
~
Output
Transf. To
LocalSpac
e
1t
M
-
¢
~
F21
M...,MM ,
Input
Connectivity
Coding
Figure 1: Overview of the compression pipeline.
tex will have a large variation over all frames and
the prediction will produce large delta vectors.
4. Transform-based coding or DCT: For further
compression, the coordinates of delta vectors are
represented as 1D signals then transformed into
frequency domain using DCT, producing uncor-
related coefficients. These coefficients are more
compressable with the entropy coding than delta
vectors. Moreover, many coefficients of low val-
ues can be zeroed without significant loss in visual
quality.
To avoid error accumulation that may occur, we
simulate the decoding process during encoding to
make sure that during the encoding, we use exactly
the same information available to decoding algorithm.
After the compression of each frame we should sub-
stitute the original vertex locations by the decoded lo-
cations.
4 COMPRESSION PIPELINE
Given a sequence of triangle meshes M
f
, f =
1, ..., F with V vertices and F frames (meshes), we
encode the first frame separately from the rest of the
frames in the sequence using static mesh compres-
sion (Gumhold and Amjoun, 2003).
An overview of the whole compression pipeline is
illustrated in Figure 1.
4.1 Local Coordinate Frames
4.1.1 Seed Triangles Selection
The first step in our algorithm is to find N seed trian-
gles upon which we construct the LCFs.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
32

Figure 2: Illustration of the local coordinate frames.
We select N seed vertex using the far distance ap-
proach (Yan et al., 2001). The first seed is selected as
the vertex corresponding to the largest euclidian dis-
tance from the geometrical center of all vertices in the
first frame. The next seeds are selected one after the
other until all N seeds are selected whereas the next
seed is selected to be the vertex with the farthest dis-
tance from the set of already selected seeds.
We associate with each seed one of its incident tri-
angles and call this triangle the seed triangle. We de-
note the three vertices of seed triangle of k-th cluster
in the f -th frame as (p
f
k,1
, p
f
k,2
, p
f
k,3
)
4.1.2 Local Coordinate Frame Construction
We assume that each cluster is initialized with the
three vertices of the seed triangle. Each cluster C
k
has
its own LCF defined on the seed triangle (p
1
, p
2
, p
3
)
as illustrated in figure 2. The origin o is the center of
one of its three edges (typically (p
1
, p
2
)), the x-axis
(red arrow) points down the edge (p
1
, p
2
), the y-axis
(green arrow) is orthogonal to the x-axis in the plane
of the seed triangle and the z-axis is orthogonal to the
x- and y-axis.
The transformation of a point p to its local co-
ordinate system q can be accomplished by an affine
transformation with a translation o and a linear trans-
formation T (T is an orthonormal matrix):
q = T(p − o)
In our algorithm, for each frame f (1 ≤ f ≤ F )
and for each cluster C
f
k
(1 ≤ k ≤ N ), we have
{T
f
k
, o
f
k
} computed from the points of the seed tri-
angle (p
f
k,1
, p
f
k,2
, p
f
k,3
).
4.2 Motion in LCF Based Clustering
The clustering process starts with several seed trian-
gles upon which the LCFs are constructed. Then the
clustering is obtained by assigning the vertices to the
seed triangle in whose LCF they have minimal local
coordinate deviation across the F frames. The cluster-
ing process consists of the following steps:
1. Initializes the N cluster C
k
, k = 1, ..., N , to be
empty. All vertices are unvisited.
Figure 3: Results of the clustering process: dance with 14,
dolphin with 9, chicken with 10 and cow with 6 clusters.
Each cluster is colored differently and encoded separately.
2. Initializes the clusters with the three vertices of
their seed triangles upon which the LCFs are con-
structed.
3. Given an unvisited vertex p
f
i
, we do the follow-
ing:
• Transform its world coordinates into the
N LCFs constructed in each frame f , so:
{q
f
1,k
, q
f
2,i
, ..., q
f
N,i
}, where f = 1, ..., F .
• Compute the total deviation (motion) of the ver-
tex between each two adjacent frames f and
f − 1 in euclidian space:
θ
k,i
=
F
X
f =1
kq
f
k,i
− q
f −1
k,i
k
2
θ
k,i
represents the total motion of the vertex i in
the LCF associated with the cluster k. A small
value means that the vertex position has motion
that is similar to C
k
. Thus the vertex should
belong to the cluster k for which the deviation
is very small, note k
min
:
k
min
:= argmin
1≤k≤N
{θ
k,i
}
• We iterate over all vertices, adding the unvis-
ited vertex whose local coordinates are almost
invariant in the LCF to the cluster C
k
and store
its local coordinates for the next step (compres-
sion).
The iteration stops if no more candidate ver-
tices exist. When a vertex is added to a cluster,
it is marked as visited. We end up with N clus-
ters that have V
k
vertices each. The results of
the clustering technique can be seen in figure 3
4.3 Differential Coding of LCFs
Generally, our approach first transforms the world co-
ordinates of each vertex into local coordinate frame
PREDICTIVE-SPECTRAL COMPRESSION OF DYNAMIC 3D MESHES
33

of its cluster. Then, it performs the compression. At
reconstruction, the local coordinates are decoded then
transformed back to world coordinates. A lossy com-
pression of the vertices of the seed triangle may dam-
age the coordinate frames at the decoding step and
as a result, the transformed local coordinates will be
damaged. Therefore, the LCF of each cluster should
losslessly encoded.
We assume that the LCFs of the first frame is al-
ready encoded. For each frame and for each new LCF,
we encode the locations of their three vertices with the
differential encoding. We subtract their coordinates
in previously encoded frame from its current coordi-
nates. We quantize the prediction differences, we ap-
ply the arithmetic coder to the resulting integers and
we update the current locations with the decoded lo-
cations.
4.4 Spatial-Temporal Predictive Coding
Once the segmentation process is finished, and all
LCFs are decoded (during the coding), the prediction
assumes that the current point does not change rela-
tive to the LCF of its cluster. So, for each new point
p
f
k,i
in the cluster C
f
k
of the frame f, one transforms
its world coordinate into local coordinates q
f
k,i
. Then,
one predicts its location from the decoded local coor-
dinates of its location in previous frame f − 1 by:
pred = ˜q
f −1
k,i
The delta vectors are computed:
δ
f
k,i
= q
f
k,i
− pred
Unlike the current predictive animated mesh com-
pression techniques (J.H. et al., 2002; Ibarria and
Rossignac, 2003; Muller et al., 2005) where the delta
vectors are encoded in world coordinate frame, here
they are computed in the local coordinates.
4.5 DCT Coding
After prediction, we represent the x,y,z coordinates of
the delta vectors of each cluster C
f
k
as 1D separate
signals of length V
k
− 3 (V
k
− 3 is the number of
vertices in the cluster C
k
, minus the three vertices of
seed triangle) and encode them with DCT coding.
For each cluster we have three signals:
X
f
k
= {x
f
k,4
, x
f
k,5
, ..., x
f
k,V
k
}
Y
f
k
= {y
f
k,4
, y
f
k,5
, ..., y
f
k,V
k
}
Z
f
k
= {z
f
k,4
, z
f
k,5
, ..., z
f
k,V
k
}
where k ∈ 1, ..., N and f ∈ 1, ..., F .
For the whole sequences, the number of signals
we obtain is N × 3 × F . We transform each sig-
nal vector into the frequency domain using 1D DCT
to obtain a more compact representation. Simple 1D
DCT is defined as:
X
f
k,l
= α(l)
V
k
X
i=4
x
f
k,i
cos(
π(l − 4)(2(i − 4) + 1)
2(V
k
− 3)
)
for l = 4, ..., V
k
, and α(l) is defined as:
α(l) =
(
1
√
V
k
−3
for l = 4
q
2
V
k
−3
for l 6= 4
The inverse DCT is similarly defined as:
x
f
k,i
=
V
k
X
l=4
α(l)X
f
k,l
cos(
π(l − 4)(2(i − 4) + 1)
2(V
k
− 3)
)
where i = 4, ..., V
k
.
After DCT transform, the majority of signal en-
ergy concentrates on the low frequencies and little on
the high frequencies. Hence the high frequencies (in-
significant coefficients) can be zeroed yielding a sig-
nificant reduction in the overall entropy and the signal
can then be represented by few high value coefficients
without significant distortion. Note that the high fre-
quencies close to zero can also be set to zero automat-
ically using quantization module only.
In our algorithm, we arrange the DCT coefficients
from high to low values to easily set the coefficients to
zero from bottom to a certain number of coefficients
depending on the compression rate and the desired
quality.
4.6 Quantization and Arithmetic Coder
The low frequency coefficient (high values) corre-
spond to the coarse details of the cluster while the
high frequency coeffients (low values) correspond to
the fine details. On the other hand the human eye can
perceive the coarse details much more accurately than
the fine details. This means that if we use a coarse
quantization or set the low value coefficients to zero,
the cluster will still retain an acceptable visual quality
and we will obtain better compression ratio.
In this version of the algorithm, we uniformly
quantize the coefficients to a user specified number
of bits per coefficient. Typically, we use a number be-
tween 8 and 12 bits, depending on how many DCT
coefficients we zeroed. The more coefficients that are
zeroed, the more coarser the quantization is, and that
better the compression will be at the expense of visual
appearance. The finer details can be preserved when
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
34

0 20 40 60 80 100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Number of coeffcients (%)
KG−error (%)
Influence of coefficient numbers
PDCT10
PDCT20
PDCT25
PDCT40
0 20 40 60 80 100
0
1
2
3
4
5
6
7
8
9
101010
Number of coeffcients (%)
Bitrate (bpvf)
Influence of coefficient numbers
PDCT10
PDCT20
PDCT25
PDCT40
(a) (b)
Figure 4: Influence of different numbers of zeroed DCT
coefficients(%): (a) on the reconstruction quality KG error
and (b) on the bitrate using different number of clusters.
only a finer quantization is used and few coefficients
are thrown away. For example, if 50% of coefficients
have zero values then we use 10 bits quantization. If
90% we use 8 bits only.
One might possibly improve on the present quan-
tization approach by introducing different levels of
quantization in each cluster. The high frequencies can
be coarsely quantized while the low frequencies can
finely quantized.
Note that, the delta vectors of the first frame are
encoded using 12 bits quantization while the delta
vectors of the LCFs in the whole sequence are quan-
tized to 16 bits.
For further compression the resulting integer val-
ues are well encoded with an arithmetic coder.
4.7 Reconstruction
To reconstruct the original data cluster, we simply de-
quantize the coefficients and perform the inverse DCT
to find out the delta vectors and add these latter to the
predicted location from the perviously decoded frame
to recover the original local coordinates. Then, we
transform them to world coordinates.
5 EXPERIMENTAL RESULTS
To show the efficiency of our coding PDCT, we mea-
sured the number of bits per vertex per frame (bpvf)
and we used the KG error metric introduced by Karni
and Gotsman (Karni and Gotsman, 2004) to measure
the distortion in the reconstruction animation with re-
gard to the original animation. We used four anima-
tions generated in different ways: the chicken, cow,
dolphin and dance sequences.
We compared the compression performance of our
algorithm against several techniques: AWC (Guskov
and Khodakovsky, 2004), TLS (Payan and Antonini,
original
9.7 bvpf, 0.009 1.2 bvpf, 0.48 0.9 bvpf, 0.49
5.9 bvpf,0.009 1.5 bvpf,0.12 1bvpf, 0.14
Figure 5: Reconstruction frame 60 of dolphin sequence,
original mesh (top arrow); using 10 clusters (middle arrow)
and 40 cluster(bottom arrow). From left to right: using dif-
ferent numbers of non-zero coefficients (%) and quantiza-
tion levels: (100%,12 bits), (2%,12 bits) and (2%,8 bits),
at various bit rates in bit per vertex per frame (bvpf) and
decoding error (KG-error).
2005), PCA (Alexa and M¨uller, 2000), KG (Karni
and Gotsman, 2004) and CPCA (Sattler et al., 2005).
Influence of Cluster Numbers: The number of clus-
ters N is an important compression parameter that af-
fects the compression performance. The bigger this
number is, the smoother the shape reconstruction will
be and the lower the bit rate that is obtained. If this
number is too small, the vertices of the same cluster
may behave differently relative to their LCF. Thereby,
the prediction in the LCF becomes poor yielding poor
compression. In opposite, If N is big, the variation of
the vertex relative to the LCF of its cluster becomes
smaller and the prediction is more effective.
Figure 4 illustrates the curves DCT coeffi-
cients/bitrate and coefficients/KG error for different
numbers of clusters.
Figure 6 also shows the rate-distortion curves for
different animations at different numbers of clusters:
chicken using 10, 25 and 40 clusters, dolphin using
10 and 40 and dance using 10, 20 and 40 clusters. We
observe that 40 clusters provide better error quality
and bit rate than using 10 or 20 clusters.
Influence of DCT Coefficients: To find the influence
of the number of DCT coefficients on the rate and on
the reconstruction of animation, we have run our cod-
ing on different resolution. Figure 4 shows the re-
sults of the number of these coefficients percent for
chicken animation. When more coefficients are dis-
carded, better compression (b) is achieved at the ex-
pense of the reconstruction quality (a).
The effect of the cluster and coefficient numbers
can also be seen in figures 5 and 7.
Influence of Quantization Level: Figure 8 illus-
PREDICTIVE-SPECTRAL COMPRESSION OF DYNAMIC 3D MESHES
35
0 5 10 15 20 25
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Bitrate (bits per vertex per frame)
KG−error (%)
Rate distortion of Chicken sequence
PDCT10
PDCT25
PDCT40
CPCA
TLS
PCA
LPC
TG
(a)
0 10 20 30 40
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Bitrate (bits per vertex per frame)
KG−error (%)
Rate distortion of Cow sequence
PDCT25
AWC
CPCA
LFS
KG
(b)
0 10 20 30 40 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Bitrate (bits per vertex per frame)
KG−error (%)
Rate distortion of dolphin sequence
PDCT10
PDCT40
CPCA
PCA
LPC
TG
(c)
0 2 4 6 8 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Bitrate (bits per vertex per frame)
KG−error (%)
Rate distortion of Dance sequence
PDCT10
PDCT20
PDCT40
(d)
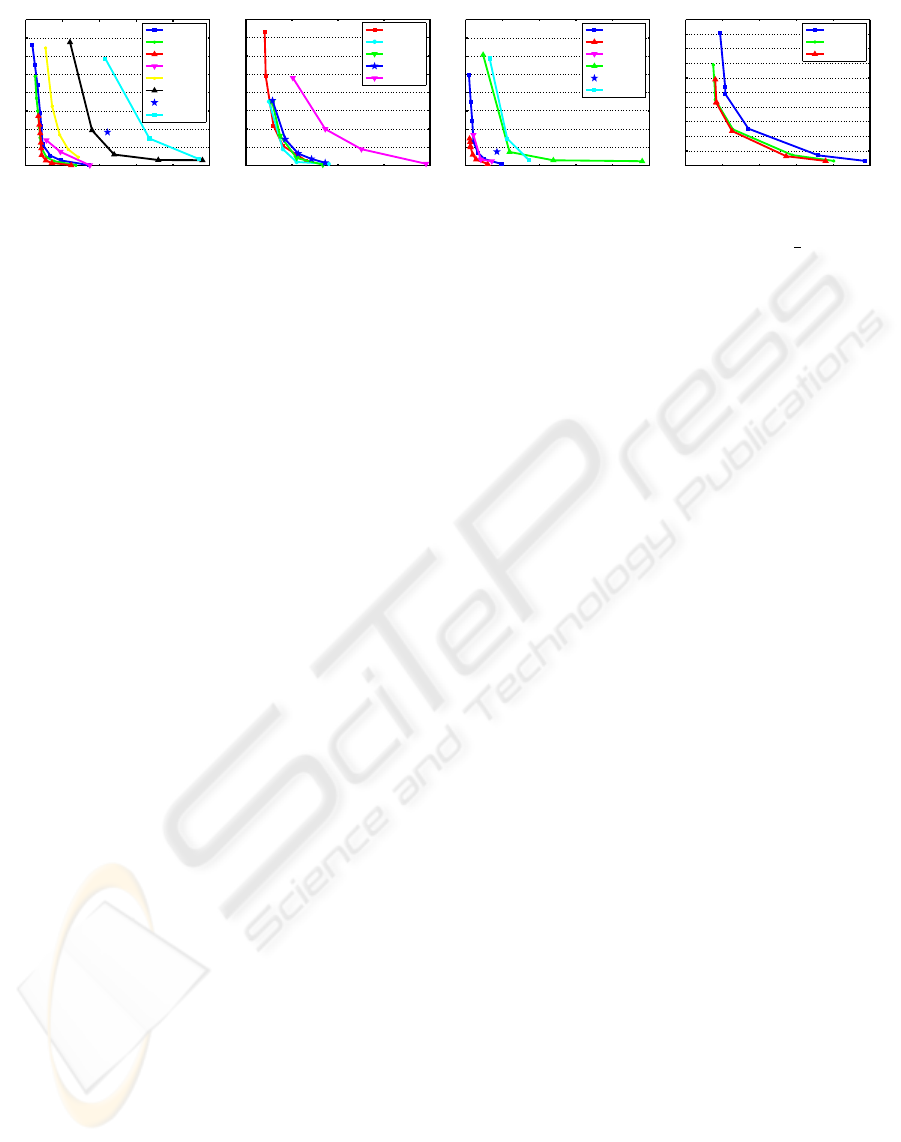
Figure 6: Rate distortion curves for the chicken (a), cow (b), dolphin (c) and dance (d) sequences using KG error.
trates the reconstruction samples of cow animation
for different quantization levels. If a coarse quantiza-
tion is used then the low value DCT coefficients will
be zeros. Consequently, the fine details are lost and
only the coarse details are detected.
Comparison to other Coders: Figure 6 illustrate the
results of running of our coder on three animations
compared with different methods. At first glance, we
can see that our approach achieves a better rate dis-
tortion performance than the standard PCA, LPC and
TG for the three models. This result is obvious since
the animation coding based on static techniques only
exploit the spatial coherence and the linear prediction
coding only uses the temporal coherence. Further-
more, the standard PCA only approximates the global
linearity and is less effective for nonlinear animation.
For the CPCA and AWC algorithms, we achieve
better or similar results. Figure 6 (b) shows that for
the cow animation which contains extreme deforma-
tions, our method is significantly better than the KG
method and comes close to the CPCA and to wavelet
based methods (LTS and AWC).
For the dolphin and the chicken sequences our
method performs better than all the above methods.
This improvement is due to the clustering of the
model into rigid parts making the prediction more ef-
ficient in the local rather than the world, coordinates.
6 CONCLUSION
In this paper we introduced a simple and efficient
compression technique for dynamic 3D mesh based
on predictive and DCT coding. First, the algorithm
clusters the vertices into a given number of clusters
depending on their motion in their LCF. This tech-
nique is simple and can be well adapted for differ-
ent purposes. Second, the location of each new ver-
tex in the current frame, is predicted from its location
in the previous frame. The effectiveness of predic-
tion coding depends strongly on the clustering pro-
cess. Indeed, if the vertices are well clustered then
the motion relative to the LCF between two succes-
sive frames tends to be zero. Third, the delta vectors
are further encoded with DCT transform to reduce the
code length since the entropy in frequency domain is
smaller than the entropy coding of delta vectors. The
resulting DCT coefficients are quantized and encoded
with an arithmetic coder.
Experimental results show that our algorithm is
competitive when compared to the state-of-the-art
techniques. In this context, it is important to note
that our coder is applicable to meshes and point-based
models regardless of how the animation is generated.
The drawback of the proposed approach is that it
doesn’t support progressive transmission. Moreover,
for a very low and fixed number of coefficients, not all
frames can be reconstructed at the same desired level
of quality.
Future Improvement: The clustering used in our ap-
proach produces clusters of different sizes. Thereby,
different numbers of DCT coefficients are produced.
If one chooses a fixed number for all clusters then
there may be too few coefficients to recover the clus-
tered vertices at a desired accuracy and possibly too
many coefficients for other clusters. Therefore, the
selection of the number of significant coefficients and
quantization level, is necessary to properly recover
the original data of each cluster with a certain accu-
racy. Therefore, we plan to introduce a rate distortion
optimization that trades off between rate and the total
distortion, overcoming the aforementioned drawback.
We also plan to develop temporal DCT in combina-
tion with predictive coding in local coordinates. This
approach is more suitable for progressive transmis-
sion. For a large sequence of meshes, the animation
may become more complex and the clustering can
produce poor prediction for some successive frames.
Therefore, we propose to cut the sequence into short
clip and update the clustering for each new coming
clip. The first frame of each clip should be encoded
spatially as I-frame.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
36

(original)
(40,12,100)
(40,12,50)
(40,12,30)
(40,12,2)
(10,12,2)
(40,8,2)
(10,8,2)
Figure 7: Reconstruction sample frames of dolphin se-
quence. The numbers in the first column are the number
of clusters, quantization level and coefficient number (%).
ACKNOWLEDGEMENTS
We would like to thank Zachi Karni and Hector
Brice˜no for providing us the animated meshes and
Mirko Sattler, Igor Guskov and Fr´ed´eric Payan for
the results of their methods. The Chicken sequence
is property of Microsoft Inc.
REFERENCES
Alexa, M. and M¨uller, W. (2000). Representing anima-
tions by principal components. Comput. Graph. Fo-
rum, 19(3).
Alliez, P. and Gotsman, C. (2005). Recent Advances in
Compression of 3D Meshes. Elsevier Science Inc.
Amjoun, R., Sondershaus, R., and Straer, W. (2006). Com-
pression of complex animated meshes. volume 4035,
pages 606–613. Computer Graphics International.
Amjoun, R. and Strasser, W. (2006). Compression of 3d
dynamic mesh sequences. Technical Report.
Figure 8: Reconstruction sample frames of cow animation
using different quantization levels. From top to bottom: 6,
8, 12 bits.
Briceno, H. M., Sander, P. V., McMillan, L., Gortler, S., and
Hoppe, H. (2003). Geometry videos: a new represen-
tation for 3d animations. In Proc. of ACM SIG./Eurog.
Symp. on Computer animation, pages 136–146.
Gumhold, S. and Amjoun, R. (2003). Higher order pre-
diction for geometry compression. In International
Conference On Shape Modelling And Applications.
Guskov, I. and Khodakovsky, A. (2004). Wavelet compres-
sion of parametrically coherent mesh sequences. In
ACM SIG./Eurog. symp. on Comput. anim.
Ibarria, L. and Rossignac, J. (2003). Dynapack: space-time
compression of the 3d animations of triangle meshes
with fixed connectivity. In SIG./Eurog. Symp. on Com-
put. Anim.
Isenburg, M. and Gumhold, S. (2003). Out-of-core com-
pression for gigantic polygon meshes. ACM Trans.
Graph., 22(3):935–942.
J.H., Y., C.S., K., and S.U., L. (2002). Compression of 3-d
triangle mesh sequences based on vertex-wise motion
vector prediction. Cir. Sys Video, 12(12):1178–1184.
Karni, Z. and Gotsman, C. (2004). Compression of soft-
body animation sequences. Computer and Graphics.
Lengyel, J. E. (1999). Compression of time-dependent ge-
ometry. In Proceedings of ACM symposium on Inter-
active 3D graphics, pages 89–95. ACM Press.
Mamou, K., Zaharia, T., and Prˆeteux, F. (2006). A skinning
approach for dynamic 3d mesh compression. Comput.
Animat. Virtual Worlds.
PREDICTIVE-SPECTRAL COMPRESSION OF DYNAMIC 3D MESHES
37

Muller, K., S. A., Kautzner, M., Eisert, P., and Wiegand,
T. (2005). Predictive compression of dynamic 3d
meshes. In Inter. Conf. on Image Processing.
Payan, F. and Antonini, M. (2005). Wavelet-based compres-
sion of 3d mesh sequences. In Proceedings of IEEE
ACIDCA-ICMI’2005, Tozeur, Tunisia.
Rossignac, J. (Chapter 54 in Handbook of Discrete and
Computational Geometry 2004). Surface simplifica-
tion and 3D geometry compression.
Sattler, M., Sarlette, R., and Klein, R. (2005). Simple
and efficient compression of animation sequences. In
ACM SIG./Eurog. symp. on Computer animation.
Yan, Z., Kumar, S., and Kuo, C. C. J. (2001). Error-
resilient coding of 3-d graphic models via adaptive
mesh segmentation. IEEE Trans. Circ. Syst. Video
Tech., 11(7):860–873.
Zhang, J. and Owen, C. B. (2004). Octree-based animated
geometry compression. In Proceedings of IEEE on
Data Compression, pages 508–517,.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
38
