STABLE HAPTIC RESPONSE FOR COMPLEX INTERACTIONS

J. Hernantes, D. Borro

CEIT and TECNUN (University of Navarra), Manuel Lardizabal 15, 20018 San Sebastian, Spain

A. García-Alonso

University of Basque Country, Manuel Lardizabal 1, 20018 San Sebastian, Spain

Keywords: Haptic Rendering, Collision Response, Virtual Environment.

Abstract: Haptic technology is quite recent and therefore in many cases it is difficult to simulate real contacts or

interactions with a high sensation of realism. Collision response methods that calculate the force-feedback

tend to cause haptic instabilities when the normal direction changes abruptly. In consequence, collision or

contact events are often difficult to render properly in sharp corners by means of haptic devices. This paper

describes a collision response method which not only provides users with a stable force feedback, but also a

comfortable and convincing haptic interaction. The experimental results show that this approach leads to a

smoother force evolution which manages to avoid discontinuities and enhances the quality in the interaction

with corners.

1 INTRODUCTION

Humans are able to perceive the environment using

all their senses. Usually sight is the predominant

sense, although some of the other senses are also

needed to perform most tasks. Sometimes, it is

necessary to perceive the environment in more detail

and all our senses are unconsciously used to obtain

the information we need. For instance, main-

tainability studies need accessibility tests to verify

whether each part of the mock-up -static object- is

accessible or not. Obviously, a visual test is not

enough to detect possible inaccessible parts or

manipulate different parts of a virtual model in order

to complete an assessment task.

Providing users with the natural ability to use all

their senses in a simulation environment is an

important goal in the Virtual Reality research area.

Within this context, haptic devices are used to

provide us with force feedback in domains where it

is needed, considerably enhancing interactivity.

Following with the example of virtual simulation

of maintainability tasks, an operator moves a virtual

tool or mobile object such as a screwdriver using the

haptic device, and collides with the different parts

that constitute an engine. The haptic forces restored

in the collision event should make the operator feel

the virtual objects like real rigid objects, and prevent

any interpenetration with the environment.

This paper focuses on the problems that virtual

corners cause in haptic interactions, in which the

force direction changes suddenly causing

instabilities in the haptic system. The proposed

algorithm manages a proper resultant penetration

and normal direction of the collision. In addition to

stability and time performance, we have paid

particular attention to provide users with a

comfortable algorithm to interact with.

Some experiments have been performed to

analyze the quality of the proposed method using a

haptic device called LHIfAM (Savall et al., 2004),

which only provides force feedback in three

translational degrees of freedom. However, it can be

used with any commercial haptic device. The results

show that this algorithm avoids abrupt changes in

the computed haptic force obtaining a more

continuous force. As a result, haptic stability is

improved in complex intersection of surfaces.

The article is organized as follows. Firstly, we

present the state of the art of the collision response

methods. Section 3 describes the specific problem

involving the computation of force feedback. After

that, the description of the proposed collision

response algorithm is presented in Section 4. Section

146

Hernantes J., Borro D. and García-Alonso A. (2007).

STABLE HAPTIC RESPONSE FOR COMPLEX INTERACTIONS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 146-153

DOI: 10.5220/0002082401460153

 SciTePress

5 discusses the effectiveness of our algorithm

analyzing the experimental results. And finally,

Section 6 summarizes the results and points out

direction for future research.

2 PREVIOUS WORK

There are several approaches which compute force

interaction for virtual objects in collision represented

by triangular meshes. The existing techniques for

haptic rendering with force display can be

distinguished based on the way the mobile object

used to interact with the environment is modelled:

point, ray or 3D object (Basdogan and Srinivasan,

2002).

In point-based haptic interactions only the end-

point of the haptic device, known as the haptic

interface point (HIP), interacts with virtual objects

(Massie and Salisbury, 1994). Zilles et al. (Zilles and

Salisbury, 1995) proposed an idealized

representation of the haptic device called god-object,

that is constrained on the surface. Ruspini et al.

(Ruspini et al., 1997) use an approach similar to the

god-object method called virtual proxy. They

represent the virtual probe as a small sphere instead

of using a point-size god-object in order to avoid

falling through the holes in the model, consequence

of an inaccurate tessellation. They also proposed

methods to smooth the object surface and added

friction. Recently, a generalization of the god-object

method for six degree of freedom has been proposed

providing a high quality haptic display (Ortega et al.,

2006).

In ray-based interactions, the virtual probe is

modelled as a line-segment and the collision points

are computed as the intersection points between the

ray segment and the surface of the object. This

representation allows users to touch multiple objects

simultaneously providing forces as well as torques

(Ho et al., 2000). Some works have shown the

advantages of this technique in medicine

applications like minimally invasive surgeries since

the probe is considered a good approximation of

long medical tools (Basdogan et al., 2004).

Nevertheless, there are some applications where

the point and ray-based methods are not accurate

enough since the working tool has such a complex

geometry that cannot be modelled using only line

segments. In these cases, it is necessary to use the

complete 3D model of the virtual tool although its

computational cost is more expensive.

Maintainability simulations are an example of

applications in which it is necessary to know

accurately the forces and torques that prevent users

from interpenetrating the virtual mock-ups.

Researchers from Boeing (McNeely et al., 1999)

have developed a voxel–based method where the

mobile objects are represented by a set of surface

point samples called Points Shell. They achieve an

acceptable performance for maintenance and

assembly task simulations. In their later works (Renz

et al., 2001, Wan and McNeely, 2003, McNeely et

al., 2006), they have presented some improvements

that enhance the performance and the haptic

stability.

Most haptic rendering methods do not attempt to

prevent the interpenetration between the virtual

objects, and compute normal forces from the

weighted average of penetration depths. Kim et al.

(Kim et al., 2003) group the contacts based on their

proximity in the 3D space, considering the most

penetrating point as the contact point. However,

these contact points can be generated and afterwards

disappear causing that normal forces change non-

continuously. Hasegawa et al. (Hasegawa and Sato,

2004) solve this problem using a spring-damper

model on the entire area of contact, which creates a

continuous change of normal forces. On the other

hand, Otaduy et al. (Otaduy and Lin, 2003, Otaduy

and Lin, 2005) create multiresolution representations

where geometric details of models are filtered when

they cannot be perceived by the user, speeding up in

this way the contact query computation for haptic

rendering. However, these methods are only valid

for convex objects, thus it is necessary to perform a

pre-process stage where all the complex objects are

simplified into convex pieces. The method presented

in this paper can also handle non-convex objects

without modifying the original mesh.

3 PROBLEM DESCRIPTION

The process of computing and generating forces in

response to user interactions with virtual objects is

known as haptic rendering (Salisbury et al., 1995).

Three main modules can be identified in a typical

haptic rendering algorithm: collision detection,

collision response and control modules. This paper

focuses specifically on the second module. Previous

works dealt with the voxel-based collision detection

approach (Borro et al., 2004) and the algorithms of

the control module (Garcia-Alonso et al., 2005).

A complete haptic rendering sequence could be

described as follows: firstly, the control module

acquires the position and orientation of the haptic

device and sends it to the collision detection module.

STABLE HAPTIC RESPONSE FOR COMPLEX INTERACTIONS

147

With this information, this module checks for

collisions between the mobile object and the

environment. If there are not collisions, it waits for

new information arising from the control module.

Otherwise, when a collision event occurs, the

contact information is sent to the collision response

module which calculates the interaction force. This

force approximates the contact forces that would

arise during contact between real objects. Finally,

the collision response module sends this interaction

force to the control module which applies it on the

haptic device and maintains a stable behaviour of the

system.

There are many methods to calculate the force

that must be restored to the user. The proposed

method in this article follows the well-known

penalty methods in which the force restored to the

user is proportional to the penetration inside the

static object. It is based on geometry and contact

planes which achieves good results not only in

computation time but also a nice perception, despite

the fact that sometimes the contact points change

discontinuously.

4 DESCRIPTION OF COLLISION

RESPONSE ALGORITHM

The final haptic response that users feel as

consequence of a collision in the virtual environment

is determined by a direction and a penetration value.

Both factors have substantial influence on users’

perception of the final force. This problem becomes

more complex when the geometry presents sharp

edges which tend to cause haptic instabilities

because of the abrupt changes in the normal

direction or in the penetration depth.

Figure 1 shows the scheme of the haptic

rendering algorithm.

Figure 1: Scheme of the haptic rendering algorithm.

When two objects collide, the group of collided

triangles of the static object constitute the “static

collision set”. The method proposed in this article

subdivides this set into areas called “contact areas”

in order to compute contact forces. Each triangle in a

contact area shares at least one edge with other

triangle in its area (see Figure 2a). This division is

helpful in order to obtain information about the

nature of the geometry in collision, making easier

the computation of the final reaction force. Next

subsections explain the phases that the proposed

collision response algorithm follows for each contact

area.

It is well-known that the simulation of non-

penetrating rigid body dynamics increases the

perceived stiffness of the environment (Srinivasan et

al., 1996). In fact, our system does not allow the

mobile object to interpenetrate visually into the

mock-ups in order to simulate realistic contacts on

the objects’ surfaces. However, we have decided to

disable this option in all figures with the purpose of

providing a clearer graphical view of the situations.

4.1 Calculate Contact Zones

In the first phase, the collision response module

subdivides the collision area into different contact

zones taking into account sharp edges (surface

discontinuities). Triangles in a contact zone are

connected among them and all the shared edges are

smooth. When two triangles share an edge and the

angle between the normals to both triangles is lower

than a fixed value (crease angle), the edge has a

“smooth label”.

There will be as many contact zones as necessary

to satisfy the smooth connectivity condition (see

Figure 2b). Each contact zone approximates a C

surface patch.

(a) (b)

Figure 2: Type of contacts. The triangles in red and green

represents the colliding triangles of the static model and

the black ones belong to the mobile object. Two contact

areas, each with two one contact zone (a) and one contact

area with two contact zones (b).

For instance, when a collision is detected in a flat

surface, all the triangles of the static object in

collision will have the same normal vector, and the

angle between them will be zero. In that case, there

will only be one contact zone. However, when the

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

148

collision is detected in a corner, there will be

different normal vectors in collision. Creating

contact zones for these cases, gives information

about the nature of the geometry in collision, and it

helps to compute a proper force feedback.

Each contact zone is represented by a zone

contact normal that is computed as the vectorial sum

of all triangles’ normals which belong to that contact

zone.

4.2 Area Contact Normal

Adequate contact normals permit providing suitable

haptic forces. Three cases can be distinguished

depending on the number of computed contact

zones.

If no triangles in the contact area share a sharp

edge, there is a unique contact zone. In case of rigid

and frictionless objects, the reaction force direction

is normal to the object surface. Therefore, the

solution is trivial since the area contact normal is the

zone contact normal.

When a contact area has two or more contact

zones, the contact has happened in an area of the

static object that is not a continuous surface (a C

area). In this case, the area contact normal must be

computed in the mobile object. It is because the fact

that the normals of static object do not provide

enough information to obtain a suitable direction

without sudden changes. This is performed using the

triangles in the mobile object that collide with the

static object. Note that this normal orientation must

be reversed.

(a) (b)

Figure 3: Contact state without C

in the static model and

mobile object (a) and solution for this problem projecting

the normal obtained (b).

However, collision situations, where there is not

a C

contact area in the static object nor in the

mobile one, often happen in real applications. These

situations often lead to abrupt changes in contact

normal in consecutive simulation steps (Figure 3).

For the purpose of avoiding these situations, the

contact normal is projected on a plane defined by the

cross product of the zone contact normals.

4.3 Penetration Depth Computation

Many good algorithms to estimate the penetration

value are known (Cameron, 1997, Kim et al., 2003,

Redon and Lin, 2006). The penetration depth value

is considered as the minimum translational distance

required to separate two objects. However, this

optimal translation could provide a non useful result,

as Figure 4 shows.

Figure 4: The minimal penetration push away the virtual

tool to the right instead of up direction.

Another problem is that in some collision states,

triangles from one object are completely inside the

other object. When this happens, those triangles do

not appear in the list of colliding triangles and

further computing should be required.

It is supposed that the stiffness of virtual

environment would be high enough to avoid large

interpenetration of objects. However, high stiff

values cause instabilities in the system; therefore a

small penetration will be allowed enabling the

existence of triangles completely inside the static

object.

The proposed method computes a fast

approximation of the penetration depth value. It is

determined by the distance from the most remote

internal vertex to the area contact plane, which is

defined by the normal computed in the previous

step. The aim is to measure the penetration in the

same direction in which the virtual tool will be

rejected to the surface.

In order to reduce the computational cost of

determining a penetration value, instead of the

global geometric problem, a local method based on a

bounding volume has been used. Spheres that cover

STABLE HAPTIC RESPONSE FOR COMPLEX INTERACTIONS

149

contact zones have been tested. For each contact

zone, the centroid is computed in order to place the

centre of the sphere and its radius will depend on the

area of each contact zone, being large enough to

contain all these vertices.

Mobile object vertices (internal vertices) that are

inside this sphere will be processed to compute the

penetration value. The zone contact normal defines

two hemi-spheres, one “internal” and the other one

“external”, referred to the static object. The vertices

of the mobile object that are in the internal semi-

sphere will be used to compute penetration.

The use of these spheres is not necessarily exact,

but simplifies the problem of finding “internal”

mobile vertices. We consider that this approximation

is specially useful when the mobile objects used to

interact with the mock-up are complex, thin and long

(Figure 5), such as the tools utilized in

maintainability tasks (screwdriver, adjustable

spanner…).

(a) (b)

Figure 5: Examples where the use of sphere could be

useful since it reduces the vertices to analyze. One contact

zone (a) and two contact zones (b).

A point is needed to define completely the area

contact plane. When there is only one contact zone,

the area contact plane is defined with the centre of

the sphere.

If there are more than one contact zone, the set of

internal vertices is the union of the internal vertices

for each zone. The common vertices among these

zones could be used to place the contact plane

(Figure 6).

nContactZone1

nFinal

nContactZone2

ContactZone1

ContactZone2

Penetration

Figure 6: Example of final haptic response: nFinal and

penetration value in yellow. The black point represents the

common point between the two contact zones.

5 EXPERIMENTS AND RESULTS

We have implemented our algorithm on a PC

running Windows XP operating system with a

Pentium Dual Core 6600, 2GB memory and an

NVIDIA GeForce 7900 GS. We have developed the

algorithm described in this paper and integrated it in

a simulation of contact interaction using 3D models

with sharp edges.

We rendered the motion of a virtual tool through

a convex corner, paying particular attention to the

speed rate and quality of force feedback, which are

the two of the most important features that a

collision response method must fulfil. As explained

before, haptic instabilities arise from the delay in the

collision detection computation and because of

abrupt changes in the haptic force value and

direction.

In order to analyze the efficiency of these two

aspects, two different types of experiments have

been accomplished. The first experiment analyzes

the influence of mobile object’s tessellation on the

penetration computation. On the other hand, the

second experiment studies the direction of computed

haptic response. We have also analyzed the users’

perception for the proposed method.

5.1 Penetration Study

The aim of this experiment is to study the influence

of tessellation on the penetration computation. This

is an important point for all methods that are based

on geometrical approximations. However, it is even

more important when a stable and comfortable

haptic response is sought. In these cases, it is

advisable to prevent large penetration values in order

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

150

to avoid abrupt changes in the force magnitude,

which might inconvenience users.

We have recorded an ideal haptic device

trajectory in which a cubic mobile object is covering

a convex edge of the virtual scenario consisted of

45.000 triangles. Then, this trajectory is played

using the same mobile object but with different

tessellation levels.

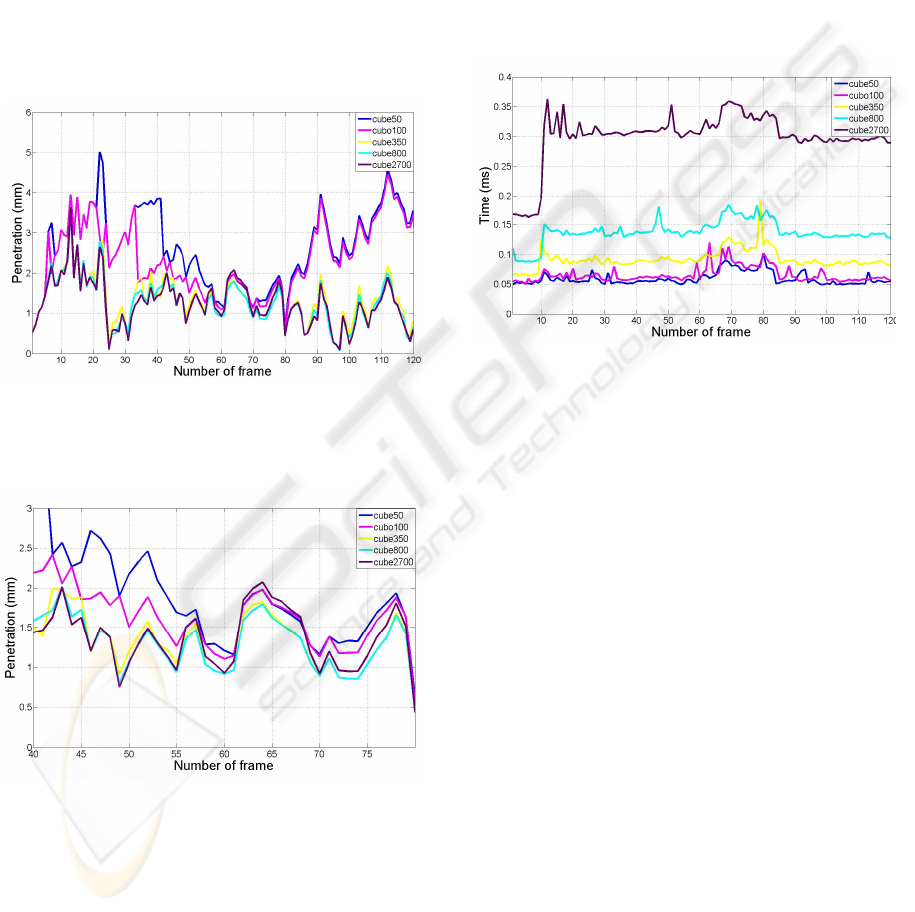
Figure 7 shows the penetration measured for

different tessellations of the virtual tool. The cube

has been non-uniformly tessellated using 50, 100,

350, 800 and 2700 triangles, which correspond to

30, 20, 10, 8, and 4 mm triangle edge length average

approximately.

Figure 7: Measured penetration depths using different

tessellations for the mobile object.

Figure 8: Detail of the previous figure from 40 to 80 frame

number.

The results show that coarse tessellations

generate important discontinuities since penetration

values and the magnitude variation between

different frames is larger than using a more detailed

tessellation. In addition to this, it can be shown that

a too detailed tessellation is not required, as we

obtain similar penetration values with the three last

levels of tessellation. Figure 8 provides a detail of

the graph where this fact can be better visualized.

We have also measured the time performance in

terms of the time required to accomplish the

different phases of the proposed method (Figure 9).

This experiment has been performed without using

the spheres which can reduce the number of vertices

to analyze in the third phase of the algorithm. The

purpose of this experiment is to show that our

method achieves good time results, which even

could be improved using the bounding volumes.

Figure 9: Time spent by the proposed method computing

the collision response.

5.2 Force Direction Study

The purpose of this experiment is to measure the

quality of the computed force. We can deduce

whether the computed force response is valid or not

analyzing the direction and module of this force.

We consider that sudden changes in the force

direction and module can result in force

discontinuities or un-stable behaviour, which can

produce a defective perception of the collision force.

Previous works (Morgenbesser and Srinivasan,

1996) have also studied the influence of abrupt

changes in the force direction and how sensitive are

humans to these changes.

In this second experiment, it has been simulated

the motion of a virtual tool through a convex corner.

To be precise, we have used a sphere of radius 50

mm and a fixed penetration of 10 mm. In Figure 10,

blue line represents the surface of the convex corner

in 2D. On the other hand, red lines are the vectorial

representations of the force computed by the

collision response methods for each point of the

trajectory.

We have compared the results of our proposed

collision response method with another method that

STABLE HAPTIC RESPONSE FOR COMPLEX INTERACTIONS

151

simply computes a haptic force with an angle of 45º

at any corner situation. As it can be noticed in the

Figure 10a, the force direction suffers abrupt

changes when entering or leaving the corner,

producing a defective perception.

(a) (b)

Figure 10: Force directions in a simulated convex edge

using a force response with an angle of 45º (a) and our

proposal method (b).

Otherwise, the proposed method provides a

progressive change in the force direction (Figure

10b), which avoids instabilities in the final force. In

this case, the user can go around feeling a rounded

corner, as it happens when we cover a real corner

using the finger.

5.3 User Perception

It is quite clear that the method that simply computes

forces in corners with an angle of 45º is not feasible

because of the instabilities and abrupt forces that it

produces.

The method proposed in this paper induces a

“rounded corner” feeling to the user, i.e., the user

can go around corners and the perceived haptic force

changes its direction in a progressive way avoiding

sudden changes in the force direction. This method

guarantees stability, but the trajectory of the

direction of the haptic force is more similar to that

when touching a cylindrical object, rather than a

sharp corner. In some way, this method imitates a

path through a real corner, but touching the corner

with one of our fingers instead of a tool. In real

world, it is easier to go around a corner with a finger

than with a tool like a pen. This is due to the fact

that the finger suffers deformation and the contact is

physically more stable.

We have made several experiments with

different users and they consider that the proposed

method is very comfortable to interact with.

Although this method does not represent accurately

the real physical reactions, users prefer this

behaviour.

We also consider that users’ perception does not

only have a technical factor but also a very

important psychological one that could be improved

using a multisensory approach to simulate haptic

applications. This multisensory concept in haptic

interfaces is being studied deeply nowadays. For

instance, factors like stereo vision, visually non-

penetrating collisions and sound can make the

system more immersive (Díaz et al., 2006) and

enhance the user perception. In a similar way, some

applications should focus more on comfortable

haptic interface than in replicating “exact” physical

behaviours.

6 CONCLUSIONS

A collision response method that deals with complex

collision interactions such sharp edges has been

presented. It avoids abrupt changes in the haptic

force direction and magnitude, improving in this

way overall stability of the haptic system.

The experiments accomplished show that this

algorithm generates continuous haptic response in

complex collisions. Users also prefer this smooth

working environment.

As future work, we are working on enhancing

the performance of the system to use it in complex

environments and extend it to support future 6-DOF

haptic interactions with torques. Moreover, we

intend to continue researching solutions to

problematic geometrical situations such as peg-in-

hole tasks and interaction with thin objects.

REFERENCES

Basdogan, C., De, S., Kim, J., Muniyandi, M., Kim, H. &

Srinivasan, M. A. (2004) Haptics in Minimally

Invasive Surgical Simulation and Training. IEEE

Computer Graphics and Applications, 24, 56-64.

Basdogan, C. & Srinivasan, M. A. (2002) Haptic

Rendering in Virtual Environments. IN STANNEY,

K. M. (Ed.) Handbook of Virtual Environments:

Design, Implementation, and Applications (Human

Factors and Ergonomics). London, Lawrence

Earlbaum Inc.

Borro, D., García-Alonso, A. & Matey, L. (2004)

Approximation of Optimal Voxel Size for Collision

Detection in Maintainability Simulations within

Massive Virtual Environments. Computer Graphics

Forum.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

152

Cameron, S. A. (1997) Enhancing GJK: Computing

Minimum and Penetration Distances between Convex

Polyhedra. IEEE International Conference on Robotics

and Automation (ICRA).

Díaz, I., Hernantes, J., Mansa, I., Lozano, A., Borro, D.,

Gil, J. J. & Sánchez, E. (2006) Influence of

Multisensory Feedback on Haptic Accesibility Tasks.

Virtual Reality, Special Issue on Multisensory

Interaction in Virtual Environments, 10, 31-40.

Garcia-Alonso, A., Gil, J. J. & Borro, D. (2005) Interfaces

for VR Applications Development in Design. Virtual

Concept'05. Biarritz, France.

Hasegawa, S. & Sato, M. (2004) Real-time Rigid Body

Simulation for Haptic Interactions Based on Contact

Volume of Polygonal Objects. Computer Graphics

Forum, 23, 529-538.

Ho, C.-H., Basdogan, C. & Srinivasan, M. A. (2000) Ray-

based haptic rendering: force and torque interactions

between a line probe and 3D objects in virtual

environments. 19, 668-683.

Kim, Y. J., Otaduy, M. A., Lin, M. C. & Manocha, D.

(2003) Six-Degree-of-Freedom Haptic Rendering

Using Incremental and Localized Computations.

Presence - Teleoperators and Virtual Environments,

Vol 12, 277-295.

Massie, T. H. & Salisbury, J. K. (1994) The PHANTOM

Haptic Interface: A Device for Probing Virtual

Objects. Winter Annual Meeting, Symposium on

Haptic Interfaces for Virtual Environment and

Teleoperator Systems. Chicago, IL, ASME.

Mcneely, W. A., Puterbaugh, K. D. & Troy, J. J. (1999)

Six Degree-of-Freedom Haptic Rendering Using

Voxel Sampling. ACM SIGGRAPH - Computer

Graphics. Los Angeles, California, USA.

Mcneely, W. A., Puterbaugh, K. D. & Troy, J. J. (2006)

Voxel-Based 6-DOF Haptic Rendering Improvements.

Haptics-e, 3.

Morgenbesser, H. B. & Srinivasan, M. A. (1996) Force

Shading for Haptic Shape Perception. The

International Symposium on Haptic Interfaces for

Virtual Environments and Teleoperator Systems.

Ortega, M., Redon, S. & Coquillart, S. (2006) A Six

Degree-of- Freedom God-Object Method for Haptic

Display of Rigid Bodies. IEEE International

Conference on Virtual Reality. Alexandria, Virginia,

USA.

Otaduy, M. A. & Lin, M. C. (2003) Sensation Preserving

Simplification for Haptic Rendering. SIGGRAPH. San

Diego, CA.

Otaduy, M. A. & Lin, M. C. (2005) Stable and Responsive

Six-Degree-of-Freedom Haptic Manipulation Using

Implicit Integration. World Haptics Conference. Pisa,

Italy.

Redon, S. & Lin, M. C. (2006) A Fast Method for Local

Penetration Depth Computation. Journal of Graphics

Tools (JGT), 11, 37-50.

Renz, M., Preusche, C., Pötke, M., Kriegel, H.-P. &

Hirzinger, G. (2001) Stable Haptic Interaction with

Virtual Environments Using an Adapted Voxmap-

PointShell Algorithm. Eurohaptics. Birmingham, UK.

Ruspini, D. C., Kolarov, K. & Khatib, O. (1997) The

Haptic Display of Complex Graphical Environments.

SIGGRAPH 97.

Salisbury, K., Brock, D., Massie, T., Swarup, N. & Zilles,

C. (1995) Haptic Rendering: Programming Touch

Interaction with Virtual Objects. ACM Symposium on

Interactive 3D Graphics. Monterey, California, USA.

Savall, J., Borro, D., Amundarain, A., Martin, J., J. Gil, J.

& Matey, L. (2004) LHIfAM - Large Haptic Interface

for Aeronautics Maintainability. International

Conference on Robotics & Automation (audiovisual

material). New Orleans, LA, USA, IEEE.

Srinivasan, M. A., G.L, B. & Brock, D. L. (1996) The

Impact of Visual Information on the Haptic Perception

of Stiffness in Virtual Environments. ASME

International Mechanical Engineering Congress and

Exposition. Atlanta, USA.

Wan, M. & Mcneely, W. A. (2003) Quasi-Static

Approximation for 6 Degrees-of-Freedom Haptic

Rendering. IEE Visualization Conference (VIS'03).

Seattle, Washington, USA.

Zilles, C. B. & Salisbury, J. K. (1995) A Constraint-based

God-object Method For Haptic Display. IEE/RSJ

International Conference on Intelligents Robots and

Systems, Human Robot Interaction, and Cooperative

Robots.

STABLE HAPTIC RESPONSE FOR COMPLEX INTERACTIONS

153