GPU-BASED CELL PROJECTION FOR LARGE STRUCTURED

DATA SETS

Andr´e Maximo, Ricardo Marroquim, Ricardo Farias and Claudio Esperanc¸a

Universidade Federal do Rio de Janeiro - UFRJ / COPPE, Brazil

Keywords:

Direct volume rendering, gpu programming, cell projection, large volumetric data.

Abstract:

We present a practical implementation of a cell projection algorithm for interactive visualization of large

volumetric data sets using programmable graphics cards. By taking advantage of the data regularity, we can

avoid computing some steps of the original algorithm with no quality loss. Furthermore, performance is

increased since more than half the processing time is dedicated only for rendering. We also provide two tools

for better user interactivity, one for transfer function editing and another for volume clipping. Our algorithm

generates high quality images at a rendering speed of over 5.0 M Tet/s on current graphics hardware.

1 INTRODUCTION

A challenging problem in medical and scientiﬁc visu-

alization is the interactive rendering of large 3D data

sets. In medical imaging, for example, most data sets

are regular (or structured) grids, usually ranging be-

tween 256

and 512

voxels. An interactive visualiza-

tion system is very important when analysing these

data sets. Efﬁciency is crucial for time-critical diag-

nostics, as well interactive manipulation of the vol-

ume data.

On the other hand, irregular (or unstructured)

grids are typically used in scientiﬁc visualization such

as geological inspection, ﬂuid simulation, among oth-

ers applications. Nevertheless, by applying a pre-

processing step, irregular data can be adapted to a reg-

ular grid. This process, known as voxelization (Kauf-

man and Shimony, 1986) (Prakash and Manohar,

1995), typically undersamples or oversamples some

portions of the volume. Better sampling strategies

have been proposed by (LaMar et al., 1999) (I. Boada,

2001) to improve the quality of the output grid.

Conversely, approaches capable of handling irreg-

ular grids, such as the Projected Tetrahedra (PT) algo-

rithm, can be easily applied to structured data, since

uniformly sized voxels may be regarded a special case

of the more general irregular grids. This, however, is

generally a bad idea since much of the computation in

such algorithms is dedicated to classifying and orga-

nizing voxels.

We present an implementation of the PT algorithm

proposed by (Shirley and Tuchman, 1990) in a spe-

ciﬁc context, where projection and sorting computa-

tions costs are virtually eliminated. More than 60% of

the time is dedicated only to the rendering pipeline.

The remainder of this paper is organized as fol-

lows: we discuss previouswork in Section 2, followed

by a quick overview of the PT algorithm in Section 3.

We then describe our approach in Section 4. In Sec-

tion 5 we present two tools for interactive manipu-

lation of the volume data. Results are given in Sec-

tion 6, and some conclusions are drawn in Section 7.

2 PREVIOUS WORK

There are many different approaches for direct

volume rendering in the literature (Kaufman and

Mueller, 2005): cell projection, ray casting and splat-

ting. With the availability of programmable cards,

new algorithms were proposed in order to exploit

Graphics Processing Units (GPUs) for interactive vol-

ume rendering.

Many cell projection algorithms have been pro-

posed for volume rendering on the GPU. Our ap-

312

Maximo A., Marroquim R., Farias R. and Esperança C. (2007).

GPU-BASED CELL PROJECTION FOR LARGE STRUCTURED DATA SETS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 312-319

DOI: 10.5220/0002082503120319

 SciTePress

proach is a variation of the GPU-based implemen-

tation of the Projected Tetrahedra technique (Marro-

quim et al., 2006).

The ﬁrst PT implementation on GPU, called

GATOR, was proposed by (Wylie et al., 2002). The

GATOR algorithm is fast yet redundant, since for

every vertex computation on the GPU all other tetra-

hedron’s vertices must be made available.

One major drawback of the PT-based algorithms is

the need of a visibility sorting of the cells. This prob-

lem has been speciﬁcally addressed on many works,

e.g. (Williams, 1992) (Stein et al., 1994) (Comba

et al., 1999), but it is not focused in this paper since

sorting voxels of a regular grid is straightforward.

The Hardware-Based Ray Casting (HARC) algo-

rithm (Weiler et al., 2003a) achieves high quality and

fast volume rendering using the GPU. However, the

memory consumption of the HARC algorithm is high

compared to other cell projection algorithms. A hy-

brid solution between cell projection and ray cast-

ing is the View Independent Cell Projection (VICP)

(Weiler et al., 2003b). By performing ray casting

only inside each projected cell, the VICP achieves

high quality image while consuming less memory

than HARC.

The main idea of the splatting algorithms, intro-

duced by (Westover, 1990), relies on the image area

inﬂuenced by each 3D data set voxel. This area,

know as footprint, is a 2D map of 3D reconstruction

kernels of the volume. The extension of Elliptical

Weighted Average (EWA) volume splatting (Zwicker

et al., 2001) proposed by (Chen et al., 2004), accel-

erates the rendering by storing the splat and volume

data on the GPU memory. The main drawbacks of

this method are the aliasing and blurring effects in the

ﬁnal image.

Level-of-Detail (LOD) techniques may also be

used in conjunction with volume rendering algo-

rithms. The idea is to undersample the 3D data set in

order to reach a speciﬁc frame rate. For instance, in

the work of (Callahan et al., 2005), interactive frame

rates are achieved by lowering the quality of the im-

age.

The work of (Roettger et al., 2003) combines ray

casting and the exploit of spatial coherence. Based

on the idea of (Danskin and Hanrahan, 1992), perfor-

mance is improved by early ray termination and space

leaping. Pre-integration techniques are used to obtain

high quality images.

In this paper, we use the partial pre-integration

technique proposed by (Moreland and Angel, 2004)

to obtain high quality images while allowing interac-

tive transfer function editing. Additionally, we adapt

the concept of footprint from splatting. In particu-

lar, we consider one unit of the volume data, i.e. a

hexahedron, as a footprint. This means that the cell

projection is only computed for one hexahedron and

replicated to the rest of the volume. With this, the

computational cost is concentrated on the actual ren-

dering of the triangles.

3 PROJECTED TETRAHEDRA

ALGORITHM

Figure 1: The different classiﬁcations of the projected tetra-

hedra.

The projection in our approach is based on the PT al-

gorithm of (Shirley and Tuchman, 1990), where the

tetrahedra are projected to screen space and composed

in visibility order. The tetrahedra’s projected shapes

are classiﬁed depending on the different number of

generated triangles (see Figure 1). With this classi-

ﬁcation, the colors and opacity values of the trian-

gle vertices are evaluated. An approximation of the

ray integral is then used to compute the color of each

triangle fragment. The ﬁnal pixel color is computed

by summing all the fragment contributions in back-

to-front order.

For each projection, the thick vertex is deﬁned as

the point of the ray segment that traverses the maxi-

mum distance through the tetrahedron. All other pro-

jected vertices are called thin vertices, as no distance

is covered. For class 2 projections (see Figure 1), the

thick vertex is computed as the intersection between

the front and back edges, while for the other classes

it is one of the projected vertices. The scalar values

of the ray’s entry and exit points are named as s

and

(see Figure 2). Thin vertices have the same values

for s

and s

, while for thick vertices these values may

have to be interpolated from those of the thin vertices.

The distance traversed by the ray segment is deﬁned

GPU-BASED CELL PROJECTION FOR LARGE STRUCTURED DATA SETS

313

as the thickness l of the cell.

Figure 2: The ray integration parameters inside one tetrahe-

dron.

Three values – s

, s

and l – are interpolated in-

side each triangle of the projected tetrahedron. To

compute the fragment color, the original PT algorithm

computes the average between s

and s

. The RGB

color and τ are then retrieved from the transfer func-

tion by this average scalar. On the other hand, the

opacity (α) value is evaluated as α = 1−e

−τl

, where

τ is the extinction coefﬁcient and l is the interpolated

thickness for that fragment.

Finally, the fragments are composed in back-to-

front order. For each new color added to the frame

buffer, the new ﬁnal color is computed as C

αC

new

+ (1 − α)C

. C

is the color already in the

frame buffer, while C

new

and α are the new color and

opacity values computed for the fragment.

4 ALGORITHM OVERVIEW

The main idea of this work is to use the PT algorithm

taking advantage of the volume data regularity. The

algorithm consists of four steps, where the ﬁrst three

steps take place in the CPU, whereas the last is per-

formed by the GPU (see Figure 3). First, the pro-

jection of a single hexahedron is determined by split-

ting it into ﬁve tetrahedra. Then, a traversal order

for the whole volume is determined in constant time.

The remaining step on the CPU consists of allocating

the volume information in a Vertex Array structure.

Lastly, triangles corresponding to the projected tetra-

hedra are rendered and composited in back-to-front

order using the GPU.

Figure 3: Algorithm overview.

4.1 Basis Hexahedron Projection

Since the PT algorithm requires a tetrahedral mesh as

input, the volumedata must be preprocessedby subdi-

viding each hexahedron into ﬁve tetrahedra. We term

each such set of tetrahedra a volume unit or volunit for

short. A key observation is that, by rendering the vol-

ume in orthographic projection, all volunits are pro-

jected to the screen in exactly the same way. Thus, to

avoid redundant computation, the projection parame-

ters are computed only once for a basis hexahedron.

Each basis tetrahedron is projected to screen co-

ordinates and its projection class is determined by

means of four cross-product tests, refer to (Marro-

quim et al., 2006) for more details. Then, the thick

vertex and the front and back scalar values can be

computed with at the most two segment intersections

(depending on the class).

For each of the ﬁve basis tetrahedra the following

projection values are computed and stored:

• basis projection class,

• basis projected vertices coordinates,

• basis thick vertex coordinates,

• basis intersection parameters for computing the

front and back scalar values,

• basis rendering order.

4.2 Rendering

To render the volume data, each tetrahedron is ren-

dered as a triangle fan. The primitives are drawn in

back-to-front order and the resulting pixel fragments

are composed using a blend function. The basis hexa-

hedron is iteratively displaced to the position of each

volunit, and the stored basis projected vertices are

used to compose the tetrahedra triangles. Each tri-

angle fan is rendered with the number of triangles rel-

ative to its basis projection class following the basis

rendering order. The ﬁrst vertex of the fan, its central

node, is the basis thick vertex.

Even though the geometry can be resolved by just

displacing the basis hexahedron, the colors and opac-

ity values are unique for each vertex and must be com-

puted on the ﬂy for each volunit. In fact, the ﬁnal

color is computed only in the GPU’s fragment shader.

The values passed as the vertex color to the render-

ing pipeline are its front and back scalar values and

its thickness.

For every vertex other than the thick vertex, the

scalar front and back values are the same (the orig-

inal scalar of the volume data). Furthermore, their

thickness value is always zero since the ray traverses

no length of the tetrahedron at these vertices. On

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

314

the other hand, the scalar values for the thick ver-

tex are calculated using the basis intersection para-

meters, while the basis thickness was already com-

puted for each basis tetrahedron. Figure 4 illustrates

a rendered triangle with color values.

Figure 4: The color values for a class 1 projection case.

4.2.1 Vertex and Fragment Shaders

Vertex coordinates are computed on the ﬂy by the ver-

tex shader based on the 3 integer indices of the ver-

tex in the lattice. This computation requires several

parameters previously determined for the basis hexa-

hedron and passed to the shader as global values, or

“uniforms” in GLSL parlance.

Each grid vertex is rendered multiple times, once

for each incident tetrahedron. Thus, along with

the vertex grid coordinates, additional information is

coded in the vertex normal, namely the tet

and the

vert

. The tet

is stored in the x normal coordinate

and identiﬁes which of the ﬁvetetrahedra is being ren-

dered. The vert

is stored in the y normal coordinate

and identiﬁes the vertex of the tetrahedron. It should

be noted that this coding scheme shifts most of the

computational load from the CPU to the GPU.

The fragment shader receives trilinearly interpo-

lated vertex colors (sf, sb, l) for each triangle frag-

ment. The interpolated scalar values are used to

lookup the chromaticity and opacity values in a trans-

fer function table. This table is stored in a 1D texture

with 256 positions. For each scalar value the trans-

fer function texture is accessed to determine its corre-

spondent RGBA color.

The Figure 5 summarizes the algorithm pipeline

in the GPU. Each volume hexahedron is sent to the

GPU as ﬁve triangle fans, while each fan corresponds

to one tetrahedron projection. The vertex shader uses

the basis hexahedron information, stored globally as

uniform variables, to correctly displace each vertex.

The rasterization process interpolates the color infor-

mation inside each triangle (see Figure 4), and the ﬁ-

nal fragment color is computed.

Figure 5: Algorithm pipeline. The 5 projected basis ver-

tices, including the thick vertex, are read in the vertex

shader. While the fragment shader reads 3 textures: ex-

ponential, transfer function, and partial pre-integration.

4.2.2 Fragment Color Computation

Given the front and back colors and thickness values,

there are some options for determining the ﬁnal frag-

ment color. The simplest and fastest way is to com-

pute the chromaticity value as the average between

the front and back colors. The opacity is computed as

α = 1− e

−τl

, where τ is the mean alpha value, and l

is the thickness. Instead of computing the exponen-

tial value on the ﬂy, a faster way is to use another 1D

texture, namely exponential texture, as a lookup table

for e

−u

, with u sampled over interval [0,1].

Another way to compute the ﬁnal color is by actu-

ally integrating the colors along the ray traversing the

tetrahedron. However, in practical terms, this is in-

feasible. The pre-integration method (Roettger et al.,

2000) is a way to achieve this result by storing the in-

tegral values for different {s

,l} in a table. A sin-

gle lookup operation returns the ﬁnal fragment color.

Nevertheless, this table is computed using the trans-

fer function implicitly, and must be recomputed every

time it changes. Since generating the pre-integration

table is an expensive operation, this cannot be done in

interactive times.

To overcome this disadvantage, the partial pre-

integration approach introduced by (Moreland and

Angel, 2004) computes a table independent of the

transfer function. The so-called ψ table does not de-

pend on any attribute of the visualization, therefore it

is pre-compiled within our implementation.

In the fragment shader, the colors associated with

and s

are retrieved from the transfer function tex-

ture. The C

and C

together with the thickness value

l are used to compute the indices of the ψ table, stored

in a 2D texture. The value retrieved from this table is

then used to compute the ﬁnal fragment color.

In contrast with the original PT method, the partial

method is slower than computing the ﬁnal color using

GPU-BASED CELL PROJECTION FOR LARGE STRUCTURED DATA SETS

315

the scalar front and back average. Moreover, the use

of partial pre-integration, instead of pre-integration,

allows interactive transfer function editing. Every

time the function is updated, the texture is reloaded

into the GPU memory.

4.2.3 Optimizing with Vertex Arrays

To achieve even higher frame rates, we make use

of the optimized OpenGL function glMultiDrawEle-

ments. The CPU–GPU transfer load is reduced by

keeping some common data among volunits stored in

the GPU memory. For each volunit three arrays are

read by this function: a vertex, a color, and a normal

array. Each array has ﬁxed size and contains ﬁve ver-

tices for each of the ﬁve tetrahedra (4 vertices plus the

thick vertex).

All coordinates, colors and normals are passed ex-

actly the same way as explained in the last section.

However, the vertex and color arrays must be recom-

puted for each volunit while the normal array can be

computed only once since it is valid for all volume

units.

The order of the vertices of the triangle fans must

be passed as an array argument to the function. Again,

ﬁve arrays of indices are created once for all volunits

with the basis rendering order.

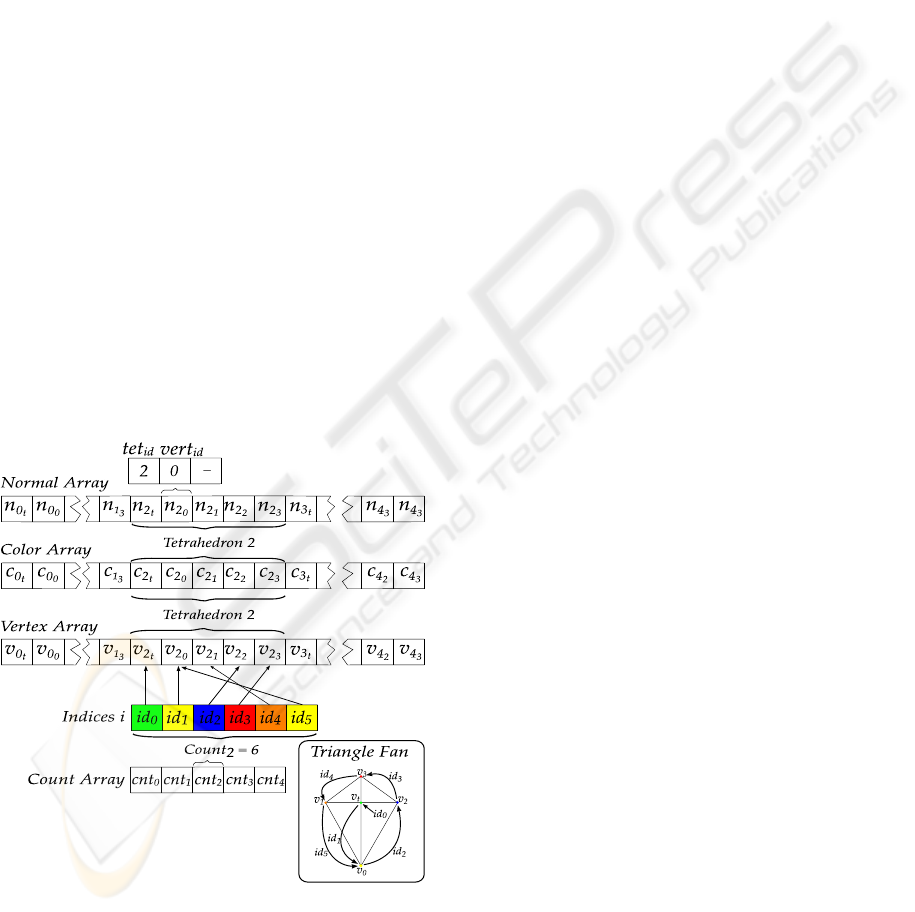
Figure 6: The vertex, color, and normal arrays structure.

Figure 6 illustrates an example of the arrays struc-

ture. In this case the third tetrahedron is of class 2 (six

vertices).

4.3 Sorting

One disadvantage of the PT algorithm is that the

primitives must be rendered in an ordered way, typ-

ically back-to-front. Sorting millions of tetrahedra

can be achieved in at most O(n) using auxiliary

data structures and by performing more costly pre-

processing operations (Williams, 1992) (Stein et al.,

1994) (Comba et al., 1999). However, we can again

proﬁt from the fact that the data is regularly spaced

and thus implicitly sorted as a 3D array. All that

remains is determining a traversal rule for this data,

which can be done in constant and negligible time. In

fact, only 8 possible traversal orders are sufﬁcient to

render the volume from any possible angle.

Let ~v = {v

} be the viewing vector, i.e, a

vector pointing to the observer. Then, a positive v

in-

dicates that the volunits must be traversed in ascend-

ing order of x indices, whereas a negative v

would

indicate a descending order. A similar rationale may

be used for the other axes. Note that the relative or-

der in which the axes are traversed does not matter

for regular data, that is, iterating in the order x, y and

z will produce the same result as iterating in z, y and

x or any other permutation.

5 VOLUME INTERACTION

The interaction with the volume data is improvedwith

two manipulation features: interactive transfer func-

tion editing and volume clipping.

The ﬁrst allows the user to interactively manipu-

late control points of the transfer function. Every time

a change occurs, the transfer function texture is re-

computed and uploaded again to the fragment shader.

The brightness of the image can also be adjusted and

acts as a global opacity factor.

The clipping tool acts directly on the volume im-

age. By selecting rectangular areas, the volume can

be trimmed and smaller features enlarged. The only

limitation is that the clipping must be parallel to one

of the volume’s bounding box sides to ensure that the

regular properties are maintained.

6 RESULTS

In the previous sections, we have described an imple-

mentation of the PT algorithm for regular data using

vertex and fragment shaders. Our prototype was pro-

grammed in C++ using OpenGL 2.0 with GLSL under

Linux. Performance measurements were made on a

Intel Pentium IV 3.6 GHz, 2 GB RAM, with a nVidia

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

316

GeForce 6800 256 MB graphics card and a PCI Ex-

press 16x bus interface.

Some results for different data sets are shown in

Table 1. All timings were taken with a 512

viewport

and considering that the model is constantly rotat-

ing. The rotation procedure is important to change be-

tween different projection classes, since parallel ren-

dering generates less triangles.

The number of vertices (# Verts) and tetrahedra (#

Tet) depends on the dimension of the original regular

data set. Performance measures are given in frames

per second (fps) and millions of tetrahedra per second

(M tet/s) for each data set. In fact, this last column

contains two values: the ﬁrst is the nominal number

of tetrahedra per second, including those which do

not contribute to the ﬁnal image, while the second is

the effective number, i.e., the tetrahedra actually ren-

dered.

Table 1: Average frames and tetrahedra per second.

Data set # Verts # Tet fps M tet/s

Fuel 262 K 1.2 M 70.78 88.5/5.99

ToothC 1 M 5 M 1.22 13.1/6.30

Tooth 10 M 52 M 0.24 12.7/6.61

Foot 16 M 83 M 0.81 67.7/6.23

Skull 16 M 83 M 0.61 51.7/6.25

Aneurism 16 M 83 M 2.42 201/5.35

We use ﬁve different data sets to measure our al-

gorithm (VolVis, 2006). The simulation of fuel injec-

tion, computed tomography of a tooth, the x-ray scan

of a human foot, skull and aneurism. The row labeled

ToothC corresponds to the original tooth tomography

clipped with our tool.

The value for tetrahedra per second (tet/s) given

in Table 1 only counts the tetrahedra which were ac-

tually rendered, since volunits with zero opacity are

discarded. The models rendered with our algorithm

are shown in Figure 7.

The timing for the vertex array setup and render-

ing are given in Table 2. In our algorithm, the aver-

age time spent in rendering is more than 60% of the

total time. It should be noted that as the time spent

in rendering the volume becomes closer to 100%, the

algorithm times will be bound by the graphics card

performance (Roettger and Ertl, 2003).

7 CONCLUSIONS AND FUTURE

WORK

In this paper we have presented a direct volume ren-

dering algorithm, based on the PT method, that takes

Table 2: Setup and render times.

Data set Setup Render % Total

Fuel 0.005 s 0.009 s 64.28 %

Tooth 1.377 s 6.484 s 82.47 %

Foot 4.556 s 9.074 s 66.57 %

Skull 4.606 s 8.593 s 65.10 %

Aneurism 0.199 s 0.210 s 51.34 %

advantage of the data regularity. The graphics hard-

ware is also explored to increase frame rates up to 6.6

M Tets/s while generating high quality images.

No extra data structures are created other than the

volume data itself. The only limitation is that the

data set must ﬁt in main memory to avoid swapping.

We’ve also created a clipping interface to easily cut

away undesirable parts of the volume, increasing the

frames rates and allowing better visualization and in-

teractivity.

Currently, each hexahedron is divided into ﬁve

tetrahedra, each of which is rendered in the worst case

as 4 triangles or a maximum of 20 triangles per volu-

nit. As future work we are investigating ideas to ren-

der less primitives by volume units.

Another improvement being considered consists

of enhancing the visualization by mixing in a Phong

lighting model (Max, 1995) where the gradient ﬁeld

is used to estimate normal vectors.

REFERENCES

Callahan, S., Comba, J., Shirley, P., and Silva, C. (2005).

Interactive rendering of large unstructured grids using

dynamic level-of-detail. In IEEE Visualization ’05,

ISBN 0-7803-9462-3, pages 199–206.

Chen, W., Ren, L., Zwicker, M., and Pﬁster, H. (2004).

Hardware-accelerated adaptive ewa volume splatting.

In VIS ’04: Proceedings of the conference on Visu-

alization ’04, pages 67–74, Washington, DC, USA.

IEEE Computer Society.

Comba, J., Klosowski, J. T., Max, N. L., Mitchell, J. S. B.,

Silva, C. T., and Williams, P. L. (1999). Fast polyhe-

dral cell sorting for interactive rendering of unstruc-

tured grids. Computer Graphics Forum, 18(3):369–

376.

Danskin, J. and Hanrahan, P. (1992). Fast algorithms for

volume ray tracing. In VVS ’92: Proceedings of the

1992 workshop on Volume visualization, pages 91–98,

New York, NY, USA. ACM Press.

I. Boada, I. Navazo, R. S. (2001). Multiresolution vol-

ume visualization with a texture-based octree. In The

Visual Computer, pages 185–197. Springer Interna-

tional.

Kaufman, A. and Mueller, K. (2005). Overview of volume

rendering. Chapter for The Visualization Handbook.

GPU-BASED CELL PROJECTION FOR LARGE STRUCTURED DATA SETS

317

Kaufman, A. and Shimony, E. (1986). 3d scan-conversion

algorithms for voxel-based graphics. In SI3D ’86:

Proceedings of the 1986 workshop on Interactive 3D

graphics, pages 45–75, New York, NY, USA. ACM

Press.

LaMar, E., Hamann, B., and Joy, K. I. (1999). Multireso-

lution techniques for interactive texture-based volume

visualization. In VIS ’99: Proceedings of the confer-

ence on Visualization ’99, pages 355–361, Los Alami-

tos, CA, USA. IEEE Computer Society Press.

Marroquim, R., Maximo, A., Farias, R., and Esperanca, C.

(2006). Gpu-based cell projection for interactive vol-

ume rendering. sibgrapi, 0:147–154.

Max, N. (1995). Optical models for direct volume render-

ing. IEEE Transactions on Visualization and Com-

puter Graphics, 1(2):99–108.

Moreland, K. and Angel, E. (2004). A fast high accuracy

volume renderer for unstructured data. In VVS ’04:

Proceedings of the 2004 IEEE Symposium on Volume

visualization and graphics, pages 13–22, Piscataway,

NJ, USA. IEEE Press.

Prakash, C. and Manohar, S. (1995). Volume rendering of

unstructured grid – a voxelization approach. In Com-

puters Graphics, pages 711–726.

Roettger, S. and Ertl, T. (2003). Cell projection of convex

polyhedra. In VG ’03: Proceedings of the 2003 Euro-

graphics/IEEE TVCG Workshop on Volume graphics,

pages 103–107, New York, NY, USA. ACM Press.

Roettger, S., Guthe, S., Weiskopf, D., Ertl, T., and Strasser,

W. (2003). Smart hardware-accelerated volume ren-

dering. In VISSYM ’03: Proceedings of the sym-

posium on Data visualisation 2003, pages 231–238,

Aire-la-Ville, Switzerland, Switzerland. Eurographics

Association.

Roettger, S., Kraus, M., and Ertl, T. (2000). Hardware-

accelerated volume and isosurface rendering based on

cell-projection. In VIS ’00: Proceedings of the confer-

ence on Visualization ’00, pages 109–116, Los Alami-

tos, CA, USA. IEEE Computer Society Press.

Shirley, P. and Tuchman, A. A. (1990). Polygonal approxi-

mation to direct scalar volume rendering. In Proceed-

ings San Diego Workshop on Volume Visualization,

Computer Graphics, volume 24(5), pages 63–70.

Stein, C., Becker, B., and Max, N. (1994). Sorting and hard-

ware assisted rendering for volume visualization. In

Kaufman, A. and Krueger, W., editors, 1994 Sympo-

sium on Volume Visualization, pages 83–90.

VolVis (2006). Volume Visualization.

http://www.volvis.org/.

Weiler, M., Kraus, M., Merz, M., and Ertl, T. (2003a).

Hardware-based ray casting for tetrahedral meshes. In

VIS ’03: Proceedings of the 14th IEEE conference on

Visualization ’03, pages 333–340.

Weiler, M., Kraus, M., Merz, M., and Ertl, T. (2003b).

Hardware-based view-independent cell projection.

IEEE Transactions on Visualization and Computer

Graphics, 9(2):163–175.

Westover, L. (1990). Footprint evaluation for volume ren-

dering. In SIGGRAPH ’90: Proceedings of the 17th

annual conference on Computer graphics and interac-

tive techniques, pages 367–376, New York, NY, USA.

ACM Press.

Williams, P. L. (1992). Visibility-ordering meshed polyhe-

dra. ACM Trans. Graph., 11(2):103–126.

Wylie, B., Moreland, K., Fisk, L. A., and Crossno, P.

(2002). Tetrahedral projection using vertex shaders.

In VVS ’02: Proceedings of the 2002 IEEE Sympo-

sium on Volume visualization and graphics, pages 7–

12, Piscataway, NJ, USA. IEEE Press.

Zwicker, M., Pﬁster, H., VanBaar, J., and Gross, M. (2001).

Ewa volume splatting. In IEEE Visualization 2001.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

318

(a) (b)

(e) (f)

Figure 7: Data sets : Foot (a), Tooth (clipped) (b), Skull (side view) (c), Skull (Bottom view) (d), Aneurism (e), Fuel injection

(f).

GPU-BASED CELL PROJECTION FOR LARGE STRUCTURED DATA SETS

319