A FUZZY PATH FINDING ALGORITHM BASED ON

ARTIFICIAL POTENTIAL FIELDS

Răzvan Tudor Tănasie

Software Engineering Department, Faculty of Automation, Computers and Electronics

University of Craiova, Bvd. Decebal, Nr. 107, Craiova, Romania

Dorian Cojocaru

Mechatronics Department, Faculty of Automation, Computers and Electronics

University of Craiova, Bvd. Decebal, Nr. 107, Craiova, Romania

Keywords: Path finding, fuzzy systems, collision avoidance, movement simulation.

Abstract: This paper will present a path finding algorithm based on a fuzzy system for a time dependent problem. The

fuzzy system uses singleton fuzzifier, product inference engine and center average defuzzifier. The

algorithm considers a static environment (the obstacles are not moving). The inputs are the space map,

which is split in squares (considered as the basic motion elements), the initial position of the wanderer and

the positions of the obstacles and the target. The algorithm computes, if possible, a path from the position of

the wanderer to the target, and uses the artificial potential field approach to compute weights for each of the

possible future positions of the wanderer. It is implemented in Microsoft Visual C++ and uses DirectX 9.0

libraries.

1 INTRODUCTION

Path finding is an important aspect of many domains

like robotics, game programming and any kind of

movement simulations. The idea of a path finding

algorithm is basically simple: given a moving object

(that will be called wanderer) in a space, a target that

object has to reach, the space map and a set of

constraints, the wanderer has to reach the target and,

while moving, it has to satisfy the constraints.

This paper will present a path finding algorithm

based on a fuzzy system for a time dependent

problem. It considers a static environment (the

obstacles are not moving). The inputs are the space

map, which is split in squares (considered as the

basic motion elements), the initial position of the

wanderer and the positions of the obstacles and the

target. The algorithm computes, if possible, a path

from the position of the wanderer to the target, and

uses the artificial potential field approach to

compute weights for each of the possible future

positions of the wanderer (Khatib, 1986).

2 FUZZY PATH FINDING

ALGORITHM

The algorithm computes the path for the wanderer in

a static environment (the obstacles don not change

their initial position) (Barraquand, 1991).

Based on the dimensions of the environment, an

n x m location map is constructed. Each location can

be:

 The wanderer;

 The target;

 Free location;

 An obstacle.

The locations are considered squares, and their

dimension is equal to the wanderer step. The map

can also be implemented as a mesh graph

(Jungnickel, 2004). An example of such a map is

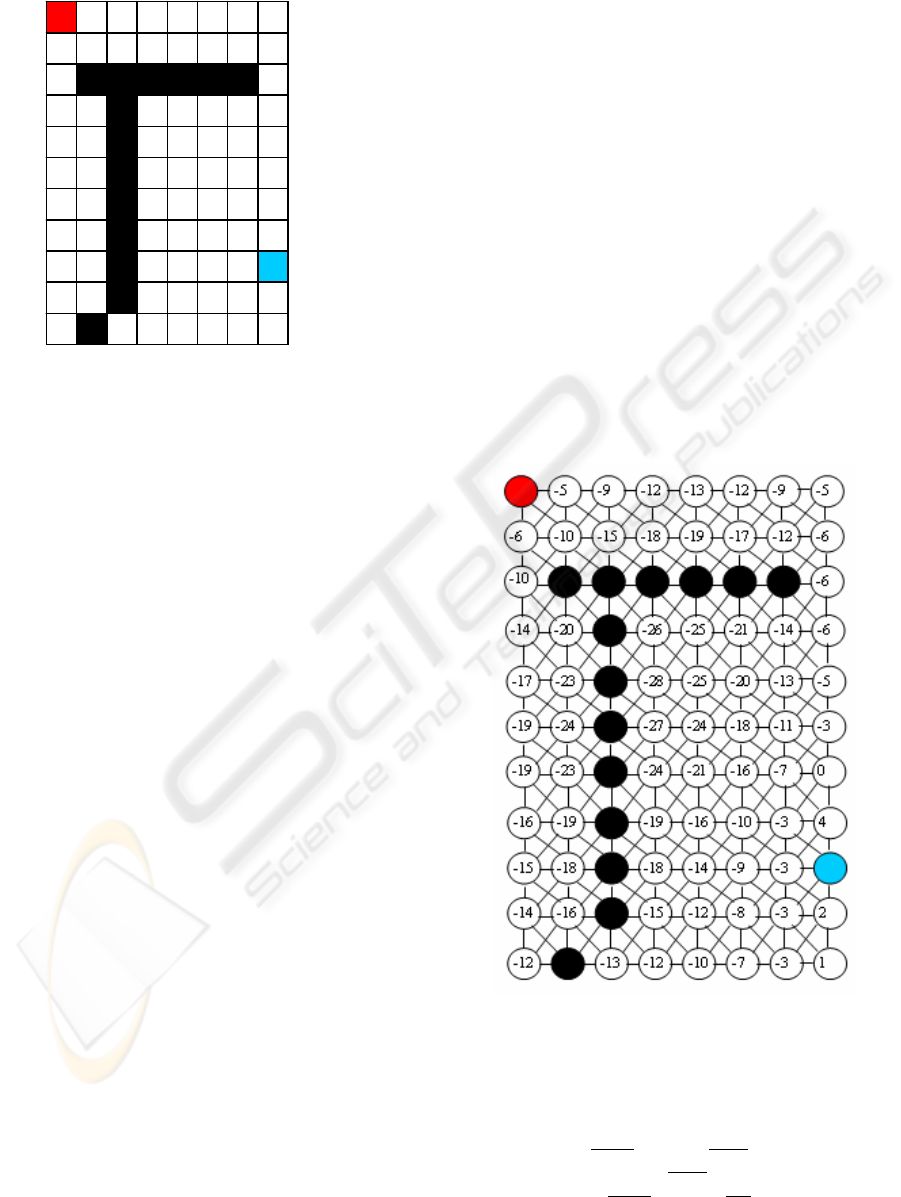
presented in Figure 1, where a black location

denotes an obstacle, a red location represents the

target, a blue location – the wanderer and a blank

location - a vacant space.

229

Tudor T

anasie R. and Cojocaru D. (2007).

A FUZZY PATH FINDING ALGORITHM BASED ON ARTIFICIAL POTENTIAL FIELDS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 229-232

DOI: 10.5220/0002083002290232

 SciTePress

Due to the fact that the obstacles are not moving,

the collisions can be avoided, but the algorithm can

not guarantee that the target will be reached. It will

end with success only if there exists at least one way

from the initial position of the wanderer to the

target.

2.1 Artificial Potential Fields

The algorithm proposed is based on the principle of

artificial potential field, more exactly, on attraction

and repulsion forces.

The scope of the wanderer is to reach the target.

This target is like an attraction pole for it, while the

obstacles are repulsion poles. In order to illustrate

this in the path finding algorithm, the target is

considered to generate an artificial field which

induces an attraction force F

, while the obstacles

generate repulsion fields that induce repugnance

forces F

. These forces are strongest near their

generator, and grow weaker while moving away

from it.

Three main ideas illustrate how these forces

work and how they generate each map position

weight:

The main goal is reaching the target:

FF <

(1)

The repulsion forces are cumulative (p is the

number of obstacles in the operation space):

∑

(2)

Each node (position) weight is given by the

composition of all the forces applied to it (W

represents the weight of node l, F

is the attraction

force generated in node l and F

is the summed

repulsion force generated in node l):

∑

+=+=

FFFFW

(3)

An example of a weighted mesh graph for the

map in Figure 1 is shown in Figure 2.

2.2 Fuzzy Rule Base

The fuzzy system is basically based on these

weights. That is, the rules composing the fuzzy rule

base are related to the weights. The wanderer makes

his decision considering the weights.

The fuzzy system contains six rules, each of

them presenting one possible situation that the

wanderer may encounter. Before applying the fuzzy

system, a simple route to the target is constructed

disregarding the obstacles (it can be the direct road

to the target). In fact, only the next step may be

computed, the others having no importance.

The six rules proved to be sufficient to

implement an efficient fuzzy path finding algorithm.

The fuzzy rule base was designed as follows:

IF X is small

and T is right

THEN Y is right

(4)

IF X is small

and T is left

(5)

Figure 1: An example of a map.

Figure 2: Weighted graph.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

230

THEN Y is left

IF X is big and T is straight

THEN Y is straight

(6)

IF X is small

and T is straight and

is big THEN Y is left

(7)

IF X is small

and T is straight and

is big THEN Y is right

(8)

IF X is small and T is straight and

is big and X

is big THEN Y is right

(9)

where X denotes the weight of the next node on the

initial path, X

- the weight of the next node’s left

neighbor with respect to the current movement

direction, X

- the weight of the next node’s right

neighbor with respect to the current movement

direction, T is the angle between the vector

indicating the current movement direction and the

vector current position-target, Y is the angle for the

next step computed by the fuzzy system.

The angles are measured with respect to the

positive sense of Ox in a trigonometric sense. The

angular differences for the motion are computed

respecting clockwise orientation.

After each step, a new unconstrained path (or

next step) is constructed.

The rules basically act in the following way:

 if the next supposed position (before applying

the fuzzy system) is under a great influence

from repulsion forces (it has a small weight)

and the target is situated to the right or left of

the current movement direction, move that

way (first two rules);

 if the next supposed position has a small weight

and the target is on the current movement

direction, move left or right (45

) depending

on which neighbor is less influenced by

repulsion fields; if the both have big weights

(i.e. the target is straight ahead, but on that

path there are a series of obstacles and there

are not other obstacles in the scene), then the

wanderer is instructed to move right (it was a

random decision, both ways having the same

result) (last three rules);

 if the target is on the current movement

direction and the next supposed position is

almost under no influence from the repulsion

forces, then the wanderer is instructed to keep

the current direction (3

rule).

In a fuzzy system like this one, each rule adds its

influence to the final result (Yen, 2000), specifically

it adds (or subtracts) a few (or many depending on

the degree of satisfaction of that rule for the current

input) degrees to the angle that indicates the next

step to be taken. The result may very possible be

different from an accessible direction (in a square

based map, only angles that are multiply of 45

indicate one step neighbors). The next position will

be chosen as the possible direction closest to the

computed value.

2.3 Fuzzy Sets and Their Membership

Functions

It can be observed from the fuzzy rule base that the

system uses five fuzzy sets that have the linguistic

labels left, right, straight, small and big.

The five fuzzy sets are divided in two categories:

 left, right, straight (Figure 3) – define

angles,

[

]

−

∈

x ;

 big (Figure 4), small – define weights

[

]

∞

−

∞

∈

,x .

The membership functions from the first

category have a Gaussian bell form, thus probability

density functions have been chosen to represent

them (Buckley, 2005). For the second category

fuzzy membership functions, cumulative distribution

Figure 3: straight membership function.

Figure 4: big membership function.

A FUZZY PATH FINDING ALGORITHM BASED ON ARTIFICIAL POTENTIAL FIELDS

231

or partial probability density functions are more

appropriate.

The chosen membership functions are:

()

exstraight

⋅−

(10)

()

⎟

⎠

⎞

⎜

⎝

⎛

+⋅−

exleft

(11)

()

⎟

⎠

⎞

⎜

⎝

⎛

−⋅−

exright

(12)

()

⎪

⎩

⎪

⎨

⎧

−<

−≥

+⋅−

Fxe

xbig

(13)

()

⎪

⎩

⎪

⎨

⎧

⋅−>

⋅−≤

⋅+⋅−

Fxe

xsmall

2,1

(14)

2.4 Defuzzification

The proposed algorithm uses singleton fuzzifier,

product inference engine, and center average

defuzzifier. From equations 12, 13 and 14 it results

that the fuzzy set straight has the center 0, the left

and right have the centers

− and, respectively

Based on the value obtained from the

defuzzifier, the next position is determined as the

nearest to that value.

3 CONCLUSIONS

Path finding is an important aspect of many domains

like robotics, game programming and any kind of

movement simulations.

This paper presented and simulated a path

finding algorithm based on a fuzzy system

(Surmann, 1996). It considered only a static

environment. The inputs are the space map, which is

split in squares, the initial position of the wanderer

and the positions of the obstacles and the target. The

algorithm computes, if possible, a path from the

position of the wanderer to the target, and uses the

artificial potential field approach to compute weights

for each of the possible future positions of the

wanderer. The results of a test from the algorithm

implementation in DirectX (Sanchez, 2000) are

presented in figures 5-7.

REFERENCES

Barraquand, J., Latombe, J.C., 1991, Robot motion

planning: a distributed representation approach, The

International Journal of Robotics Research.

Buckley, J., 2005, Studies in Fuzziness and Soft

Computing, Springer, Berlin.

Jungnickel, D., 2004, Graphs, Networks and Algorithms,

Springer, 2

edition.

Khatib, O., 1986, Real-time Obstacle Avoidance for

Manipulators and Mobile Robots, International

Journal for Robotics Research, (5)1, p90-98.

Sanchez, J., Canton, M., 2000, DirectX 3D Graphics

Programming Bible, IDG Books Wordwide.

Surmann, H., Huser, J., Wehking, J., 1996, Path planning

for a fuzzy controlled autonomous mobile robot, Fifth

IEEE International Conference on Fuzzy Systems,

New Orleans.

Yen J., Langari R., 2000, Fuzzy logic, intelligence, control

and information, Prentice Hall, New York.

Figure 6: Intermediate position.

Figure 5: Initial position.

Figure 7: Final position – target reached.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

232