INTERACTIVE RENDERING OF MULTIPLE SCATTERING

IN PARTICIPATING MEDIA

USING SEPARABLE PHASE FUNCTION

Zheng Gong, Zhimin Ren

State Key Laboratory of CAD&CG, Zhejiang University, Hangzhou, China

Zhangye Wang, Qunsheng Peng

State Key Laboratory of CAD&CG, Zhejiang University, Hangzhou, China

Keywords: Multiple scattering, participating media, phase function, singular value decomposition.

Abstract: This paper presents an interactive method to compute multiple scattering in non-homogeneous participating

media with an effective phase function approximation. The volume is represented by grids, which allows us

to render dynamic scenes. We achieve interactive computation rate by factorizing the phase function in

transport equation with singular value decomposition (SVD) and keeping only the first few low-order

approximation terms. These terms are paired 2D incident-direction texture maps and 2D outgoing-direction

texture maps. The complicated integral calculation of in-scattering in each rendering pass is efficiently

approximated by simply retrieving data from textures. Graphics hardware is also employed for on-the-fly

computation. Using the proposed algorithm, we demonstrate rendering of multiple scattering in dynamic

scenes at interactive rates.

1 INTRODUCTION

Realistic rendering in participating media has been a

long standing and difficult problem in computer

graphics. A detailed overview of rendering

techniques in participating media can be found in

(Cerezo, 2005). Back in the early 1990s, the Monte

Carlo light tracing by (Pattanaik, 1993) uses a

sampling process to calculate the points of

absorption or scattering of the bundles within the

volume. Later (Jensen, 1998) introduced photon

mapping to volume containing photons in the

participating media. Both of these methods can

accurately simulate complicated lighting models.

However, they are far from interactive. Nowadays,

solution times with the fastest Monte Carlo approach

still may take dozens of minutes.

Graphics hardware advanced rapidly in recent

years, resulting in emergences of a great number of

techniques that improve realism in near real-time.

Most of the algorithms adopt simplified physics

models or have constraints on media type. To name

a few of these algorithms, (Harris, 2001) proposed a

real-time cloud shading technique, but only multiple

scattering in forward direction was precomputed.

(Sloan, 2002) achieved interactively rendering

multiple scattering assuming isotropic phase

function and distant illumination. (Premože, 2004)

provided a method that avoids direct numerical

simulation of multiple scattering through spatial

spreading. However, this approach only considered

the overall statistics of the phase function, not its

particular shape. (Hegeman, 2005) modified the

previous method with hardware acceleration and

achieved interactive rendering rates.

(Szirmay-Kalos, 2005) suggested a real-time

method to compute multiple scattering in non-

homogeneous participating media having general

phase functions. This implementation adopted

particle system and solved the transport equation

iteratively with little simplification. Real-time

performance was achieved by reusing light

scattering paths that were generated with global line

bundles traced in sample directions in a pre-

processing phase. Nevertheless, once the particle

moves, the light scattering paths have to be re-

calculated, which is a time-consuming job. Thus, the

volume is supposed to be static. In our paper, we

262

Gong Z., Ren Z., Wang Z. and Peng Q. (2007).

INTERACTIVE RENDERING OF MULTIPLE SCATTERING IN PARTICIPATING MEDIA USING SEPARABLE PHASE FUNCTION.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 262-268

DOI: 10.5220/0002084002620268

 SciTePress

Figure 1: The appearance of participating media changes as the medium density is decreased from left to right. Multiple

scattering appears distinctive in the image on the left and is less obvious in the one on the right. Results are produced by

the proposed method at 2fps. The scene is illuminated by area light.

propose a method to solve the transport equation in

volume represented by grids rather than particles. As

a result, the calculation for the light scattering paths

is avoided. With this approach, we realize rendering

dynamic scenes.

Separable decomposition technique was

introduced by (Kautz, 1999), and it has been used

for BRDF rendering. Later (Wang, 2004) and (Liu,

2004) applied singular value decomposition (SVD)

to glossy BRDFs in PRT. In addition, (Wang, 2005)

introduced SVD to the approximation of BSSRDFs

by separating Henyey-Greenstein (HG) phase

function. Similarly, our proposed method

decomposes HG phase function in the rendering of

multiple scattering in participating media in order to

accelerate the computation.

2 BACKGROUND

2.1 Multiple Scattering in Participating

Media

When light travels in participating media, its

radiance undergoes changes due to emission, in-

scattering, absorption and out-scattering. The former

two phenomena increase the radiance, while the

latter two reduce it. The differential transport

equation of radiance

L in distance dx

is:

The increased radiance by emission can be

expressed as

() ()

, where

()

is the

emission density, and

()

is the absorption

coefficient, which is related to the density of

participating media at point

·Absorption and out-scattering are respectively

represented by

()()

and

()()

, where

()Lx

is the radiance at point

()

is the

scattering coefficient, and it is also related to density.

· In-scattering is due to photons originally

moving in a certain direction being scattered into the

considered direction. The number of scattered

photons from differential solid angle

equals to

where

(,)

is the phase function. The phase

function can be interpreted as the scattered intensity

in direction

, divided by the intensity that would

be scattered in that direction if the scattering were

isotropic (i.e. independent of the direction).

denotes the set of directions on the sphere around

point

The simplest phase function is the isotropic one.

Rayleigh phase functions are used to model

scattering processes produced by spherical particles

whose radii are smaller than around one-tenth the

light wavelength, while Mie phase functions are

generally used when particle size is comparable to

the radiation wavelength (Cerezo, 2005). In this

paper, we take scattering in clouds and fog as

examples, so the simple mathematical

approximation of Mie phase functions, HG phase

functions(Henyey, 1940)(Cornette, 1992), is used in

our transport light model. The HG phase function is:

where

(1,1)g

∈

−

is the media property describing

how strongly the media scatters forward or

backward, and

denotes the angle between

and

(, )

() (, ) ()(, )

()

()(, ) (, )( , )

emission absorption

sii

out scattering

in scattering

dL x

xL x xLx

xLx Lx p d

αα

κωκω

κω ωωωσ

−

=−

−+

∫

rr rr

14424431442443

rr r

1442443

144444

444443

(1)

()

(, )( , )

Lx p d

ωω σ

∫

(2)

()

12cos

−

+−

(3)

INTERACTIVE RENDERING OF MULTIPLE SCATTERING IN PARTICIPATING MEDIA USING SEPARABLE

PHASE FUNCTION

263

Figure 2: Phase Function (3).

The scattering properties of materials is depicted

with the Figure 2, which is a plot of HG Phase

function (3), where

is respectively 0.5, 0.4, 0.35,

and 0.25.

2.2 Singular Value Decomposition

(SVD) Factorization

In Mathematics, separable decompositions can

approximate (to arbitrary accuracy) a high-

dimensional function

with a sum of products of

lower-dimensional functions

g and

h :

Separable decompositions are usable for

remarkably compressing the original function

when a good approximation can be found with a

small

. In addition, they are capable of dividing

variables into separate expressions, namely

and

. Further calculation which involves one

variable may not need to refer to function

but to

only one of the post-decomposition functions

g or

h instead. Redundant calculation can be avoided

by adopting separable decompositions.

With the introduction of separable

decomposition into pre-computing phase function in

radiant Equation (1), the calculation speed is

expected to be drastically enhanced. In this paper,

we adopt the SVD method of decomposing phase

function in order to considerably reduce the

rendering time. We use SVD because it can produce

relatively optimal approximations (Kautz, 1999).

SVD of matrix

is the factorization that

USV=

where

[

]

Uu=

[

]

Vv=

and

(

)

Sdiag

. S is a

diagonal matrix of singular values

. As a result,

after SVD, each function

(, )

can be

approximated as:

3 THE PROPOSED METHOD

In this section, we elaborate our method for

approximating transport equation using separable

phase functions. We also present error estimation of

our approximation compared with the original phase

functions.

3.1 Discretization of the Transport

Equation

The transport Equation (1) can be discretized into

the form

where

D is the number of sample directions. The

above equation can be solved by iterations. Suppose

at iteration step

n , we have the light radiance ()

the light radiance of step

can be obtained after

one iteration:

where

() () ()

κκ

. For physically

visible materials, this iteration is convergent.

3.2 Separable Phase Function and

Error Estimation

3.2.1 Factorizing the Phase Function

In the general phase function

(,)

represents the incident light, and

is the arbitrary

outgoing light. We can sample the

directions in

the whole direction space and construct a

matrix

A . Each element in column

and row

represents the value of

(,)

. We apply

SVD on

A and obtain:

SVD approximates the multivariate phase

function

(,)

as a sum of products of functions

(, ) () ()

xy g xh y

≈

∑

(4)

(, ) () ()

kk k

xy u xv y

≈

∑

(5)

(, )

() (, )

()(, ) ()(, )

()

(, ) ( , )

emission

absorption out scattering

in scattering

dL x

xL x

xLx xLx

Lx p

κω

ωκ ω

ωω

−

≈

−−

∑

1442443

rr rr

442 4 431442 4 43

444442444443

(6)

(,)(,)

() (, ) () (, )

()

(, ) ( , )

emission out scattering absorption

in scattering

Lxdx Lx

Lx dx xLx dx

Lx p dx

ωω

κωκω

ωωω

−

+≈ +

−

∑

rrrrr

444

4443144

443

444444

4444443

(7)

(,) ()().

ikkki

puv

ωω

≈

∑

(8)

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

264

u and

of lower dimensionality. In Equation (8),

is the number of terms used in approximation. By

this approach, phase function is divided into two

parts

()

and

()

, which are only pertinent

with

and

respectively. Consequently, the

phase function is approximated by a few low-order

terms. Each of them can be represented by a 2D

texture map

()

kk i

respectively

indexed by the incident direction

or an outgoing

direction

. We name

()

incident-

direction map and

()

kk i

outgoing-direction

map.

We observe that

(,)

only varies with the

angle between

and

, so

should be real

symmetric. Symmetric matrix

A can be diagonalized

into the form

QMQ=

, where diagonal element of

are the eigenvalues of

, and the column

vectors of

Q are the corresponding eigenvectors. As

described in Section 2.2, matrix

can be factorized

with SVD into

USV=

. In this case,

UVQ

and

SM=

, so

()

and

()

kk i

should

only differ by the sign.

After applying SVD to the phase function, the

iterative transport equation is transformed into,

3.2.2 Error Estimation of SVD

Approximation

SVD can be applied to general phase functions, and

the approximation can be arbitrarily accurate. We

are going to demonstrate the result of our

approximation of phase functions with cloud

rendering. In this case, HG phase functions

(Equation (3)), are most frequently adopted.

Therefore, we present the root mean squared error

(RMES) of SVD approximation for HG phase

functions here. We apply SVD to HG phase

functions and obtained the RMES, which is shown

in Figure 3.

From the bellow figure, the approximation takes

greater number of terms to achieve certain accuracy

grows. The RMSE of SVD is about 10% for

approximations of 24 terms when

equals 0.5. It is

a numerically acceptable approximation, and it is

used for cloud rendering in this paper.

Relative RMSE of HG SVD

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

1 3 5 7 9 111315171921232527

Number of Approximated Terms

RMSE

g = 0.25

g = 0.35

g = 0.40

g = 0.50

Figure 3: Relative RMSE of HG SVD.

4 IMPLEMENTATION

4.1 Precomputation

We use the software MATLAB for precalculating

the SVD results of phase functions. The incident-

direction map

()

and outgoing-direction

map

()

kk i

are precomputed and respectively

stored in textures: Incident-Direction Texture and

Outgoing-Direction Texture. Both of them are 2D

textures indexed by column number

(1, )kN∈ and

row number

(1, )iD

∈

In Figure 4, we plotted the original HG phase

function values and the approximated HG phase

function values after applying SVD, using 8 and 24

approximating terms respectively.

4.2 Runtime Rendering Pipeline

We represent our grids with what is called a flat 3D

texture (Harris, 2003). A flat 3D texture represents

actually a 3D volume, as shown in Figure 5. Flat 3D

textures can be updated in a single rendering pass.

Figure 4: Original HG Phase Function and SVD-

Approximated HG Values Plotted Using 8 and 24 Terms.

(,)(,)

() (, ) () (, )

()

() (, ) ()

emission out scattering absorption

kk d kk d

in scattering

Lxdx Lx

xL x dx xL x dx

uLxvdx

ωω

κωκω

ξω ωξω

−

+≈

+−

∑∑

rr r

rr r rr r

14442 4 4431442443

144444444424444444443

(9)

INTERACTIVE RENDERING OF MULTIPLE SCATTERING IN PARTICIPATING MEDIA USING SEPARABLE

PHASE FUNCTION

265

This means that a 3D simulation can be

implemented in the same number of passes as that

required by an equivalent 2D simulation. Thus, it

provides a quick and inexpensive way to perform 3D

simulation.

(a) (b)

Figure 5: 3D texture (a) and its corresponding flat 3D

texture (b).

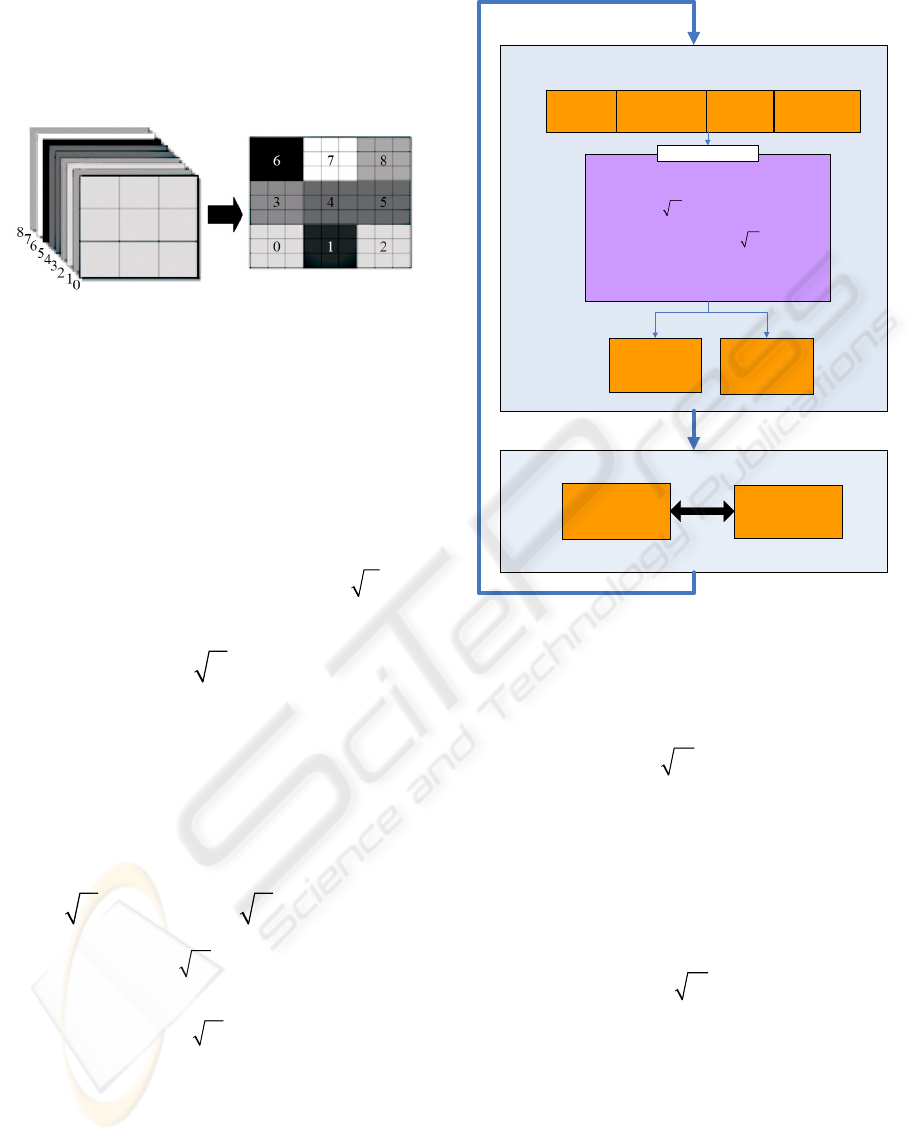
This section presents the rendering pipeline with

hardware acceleration during runtime. In every pass

of fragment program, we input Density Texture,

Radiance Texture, Incident Texture and Outgoing

Texture at iteration step

to update the values of

step

1n +

. The Density Texture and the Radiance

Texture respectively contain the density and

radiance values at each point in the rendering

volume. The Incident Texture indexes

()

with

k , and the Outgoing Texture contains the value

for each

k at each point. The rendering pipeline at

runtime is illustrated in Figure 6.

For each iteration, the process runs through the

fragment program a number of

times. During

each pass of fragment program, the radiance

(,)

Lxdx

in direction

(1, )dD∈

is updated

with Equation (9), and

() (, ) ()

kk d kk d

uLxvd

ξω ωξω

∑∑

(11)

is also calculated.

()

is indexed from

Incident Texture, and

is indexed from Outgoing Texture. In this way, the

original integral calculation:

in Equation (9) is avoided by simply retrieving

values from a texture.

Figure 6: Implementation Pipeline.

It remarkably reduces required calculation amount

during every rendering pass, thus the rendering

speed is considerably increased. At the same time,

(, ) ( )

dkkd

Lx v

ξω

(14)

is added to the Temporary Outgoing Texture for

each

(1, )kN

∈

, and d is increased afterwards.

When

d reaches D , an iteration is complete. Thus

(, )

in all D directions has been updated.

Meanwhile, the value of each grid in the Temporary

Outgoing Texture has been updated to be

Temporary Outgoing Texture and the Outgoing

Texture are switched for the next iteration. Iteration

continues, and eventually

(, )

differs little

with

(, )

, which indicates the convergence of

iteration.

(, ) ( )

dkkd

Lx v

ξω

∑

(10)

(, ) ( )

dkkd

xvdx

ωξ ω

∑

(12)

(, )( , )

Lx p

ωω

∑

(13)

(, ) ( )

dkkd

Lx v

ξω

∑

(15)

Density

Texture

Outgoing

Texture

Temporary

Outgoing

Texture

Fragment Program

1. Update ( , ) with ( , ) and

(, ) ( )

2. Accumulate ( , ) ( )to

Temporary Outgoing Texture

3. Increase

dkd

Lx Lx

Lx v

ωω

∑

Incident

Texture

ACCUMULATE

Loop of (1, )dD

∈

Radiance

Texture

Radiance

Texture

UPDATE

Temporary

Outgoing

Texture

Outgoing

Texture

SWITCH

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

266

5 RESULTS AND DISCUSSIONS

The proposed technique has been implemented in

Direct3D/HLSL environment and run on an

NV7800GT graphics card. The volume resolution is

64 64 64××

In Figure 1, we demonstrate the appearance of

multiple scattering in participating media with

different uniform densities. The scene is illuminated

with parallel light rays travelling downwards from a

window in the ceiling. The number of discrete

directions,

D , is 128. The albedo is 0.9. The

multiple scattering is more representative in medium

with a larger density, while single scattering

dominates the scene of smaller density. We compute

one iteration in each frame, and when the uniform

density changes, we take the solution of the previous

frame as the initial value of the iteration, which

results in fast convergence. The scene is simulated

as 2fps. A dynamic scene is rendered interactively.

In Figure 7, we follow the converging process of

a piece of cloud after different iteration steps. The

image on the left displays the cloud after 20

iterations. At that time, the part closer to the sun is

firstly illuminated. In the images in the middle, the

energy gradually transports to other parts of the

cloud. Notice that the thicker part of the cloud

appears darker because of high extinction. The

image on the right shows the final stable appearance

of the cloud, which indicates the convergence of

transport equation. The number of discrete

directions

D is 256, and 1.5fps was achieved.

In Figure 8, we present an example of HG phase

function factorized by SVD. The image on the left is

rendered without factorizing the phase function. On

the right is an image shaded with our method, using

24-term SVD approximation.

is 0.5 in both

simulations. From the comparison, the cloud appears

a little darker in our proposed model, especially in

the thick part. It is due to that the reconstructed

value of the phase function with our method is

generally smaller than the original one, and phase

function is only related to the in-scattering part of

the transport equation. Therefore, the approximated

in-scattering energy is smaller than the actual value.

However, a rendering speed of 1.5fps is achieved

with the proposed algorithm compared with 0.2fps

of the unfactorized model. Moreover, visually good

results are obtained by the approximation. With our

approach, rendering speed is considerably enhanced,

while realism is mostly preserved.

Original N = 24

Figure 8: SVD factorization example, illuminated by the

sun.

6 CONCLUSIONS

We have presented a method for interactively

rendering multiple scattering in participating media

with little physics simplification and constraints on

media type. Compared with the Monte Carlo

rendering method, our approach achieves much

higher rendering speed. Meanwhile, compared with

other near real-time algorithms, such as (Harris,

2001) and (Sloan, 2002), ours has little constraints

on the lighting conditions. The material properties

and the scattering phase function. We approximate

phase functions in transport equation with singular

value decomposition. Using the proposed algorithm,

rendering of dynamic scenes can be implemented

with grid system. This technique greatly reduces the

required calculation amount and enhances the

20 iterations 40 iterations 60 iterations

Figure 7: A cloud illuminated at sun set. The images show appearances of the cloud with different iteration steps.

INTERACTIVE RENDERING OF MULTIPLE SCATTERING IN PARTICIPATING MEDIA USING SEPARABLE

PHASE FUNCTION

267

rendering speed. The proposed method successfully

models dynamic scenes that do not change rapidly.

However, as to highly dynamic scenes, the

transport equation takes more time to converge.

Once the change occurs before the convergence,

error appears and accumulates successively.

Therefore, we plan to focus on developing a

better model which converges faster in future work.

ACKNOWLEDGEMENTS

This research is supported by 973 program of China

under grant 2002CB312101, the National Natural

Science Foundation of China under grant 60603076

and 60475013.

REFERENCES

Cerezo, E., Pérez, F., Pueyo, X., Seron, F. J., Sillion, F. X.,

2005. A Survey on Participating Media Rendering

Techniques. In The Visual Computer 21, pp. 303-328,

2005.

Cornette W., Shanks J., 1992. Physical reasonable analytic

expression for single-scattering phase function.

Applied Optics 31, 16, 31–52, 1992.

Harris, M. J., Lastra, A., 2001. Real-Time Cloud

Rendering. In Proceedings of Eurographics 2001,

20(3):76-84, September 2001.

Harris, M. J., Baxter W. V. III, Scheuermann T., Lastra

A.. Simulation of Cloud Dynamics on Graphics

Hardware. In Proceedings of Graphics Hardware

2003.

Hegeman, K., Ashikhmin, M., Premoze, S., 2005. A

Lighting Model for General Participating Media. In

Proceedings of ACM SIGGRAPH Symposium on

Interactive 3D Graphics and Games, April 2005.

Henyey, G., Greenstein, J., 1940. Diffuse radiation in the

galaxy. Astrophysical Journal 88, 70–73, 1940.

Jensen, H. W., Christensen, P. H., 1998. Efficient

simulation of light transport in scenes with

participating media using photon maps. In

Proceedings of ACM SIGGRAPH 98, 311--320.

Kautz, J., McCool, M., 1999. Interactive Rendering with

Arbitrary BRDFs using separable approximation. In

10th Eurographics Workshop on Rendering, 1999, pp.

255-268, 379 (colour plate).

Liu, X., Sloan, P.-P., Shum, H.-Y., Snyder, J., 2004. All-

Frequency Precomputed Radiance Transfer for Glossy

Objects. In Eurographics Symposium on Rendering

2004, pp.337-344, 2004.

Pattanaik, S. N., Mudur, S. P., 1993. Computation of

Global Illumination in a Participating Medium by

Monte Carlo Simulation. In The Journal of

Visualization and Computer Animation, 4(3):133–152,

July - September 1993.

Premože, S., Ashikhmin, M., Tessendorf, J.,

Ramamoorthi, R., Nayar, S., 2004. Practical rendering

of multiple scattering effects in participating media. In

Proceedings of the Eurographics Symposium on

Rendering 2004.

SLOAN, P.-P., KAUTZ, J., SNYDER, J., 2002.

Precomputed radiance transfer for real-time rendering

in dynamic, low-frequency lighting environments. In

ACM Transactions on Graphics 21, 3 (July), 527–536.

Szirmay-Kalos, L., Sbert, M., Ummenhoffer, T., 2005.

Real-Time Multiple Scattering in Participating Media

with Illumination Networks. In Proceedings of the

Eurographics Symposium on Rendering 2005.

Wang, R., Tran, J., Luebke, D., 2004. All-frequency

relighting of non-diffuse objects using separable

BRDF approximation. In Proceedings of

Eurographics Symposium on Rendering 2004, pp.345–

354, 2004.

Wang, R., Tran, J., Luebke, D., 2005. All-frequency

interactive relighting of translucent objects with single

and multiple scattering. In ACM Transactions on

Graphics, 24(3): 1202-1207.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

268