A FRAMEWORK FOR INTERACTIVE GPU-SUPPORTED

RENDERING AND STYLING OF VIRTUAL HAIR

Rui (Ray) Zhang and Burkhard C. Wünsche

Department of Computer Science, Private Bag 92019, University of Auckland, New Zealand

Keywords: Hair modelling, interaction techniques, GPU algorithms, wisp model, key strands.

Abstract: The interactive styling and rendering of virtual hair is essential for creating realistic looking human avatars

for use in computer games, virtual worlds, and movie special effects. Hair models can contain tens of

thousands of hair strands and hence it is important to develop techniques to modify the hair in a realistic

fashion and to render it at interactive frame rates. In this paper we present a GPU-based framework for

styling and rendering of virtual hair. We use wisps to represent basic units of hair strands and present an

improved statistical model for hair wisp generation which allows the creation of smooth and fringy styles.

Fast modelling is achieved by using create, edit, delete and copy and paste operations for key strands

representing wisp. The styling process is simplified by using a local coordinate system for hair strands in

order to define preferred styling (brushing) directions. Fast photo-realistic rendering is achieved by using

the latest GPU functionalities for both the light reflection calculation and the shadow generation of hair

strands. We also propose a new method for real-time anti-aliasing using GPU programming.

1 INTRODUCTION

Computer generated realistic virtual humans are

required in applications such as the movie industry

(CGI – computer generated imagery), computer

games, and as avatars for virtual worlds. An

important factor for achieving a realistic human

appearance is the development of a realistic hair

model. Psychological studies have shown that hair is

a determining factor of a person’s first impression

when meeting his or her counterpart (Lafrance,

2005). Therefore, the styling and rendering of virtual

hair is an active field of research in Computer

Graphics. Hair styling is challenging since the

complex behaviour of each hair strand and the

interactions among the hair strands during animation

and styling must be controlled in a physically

realistic way.

In this paper we present a GPU-based framework

for styling and rendering of virtual hair. Section 2

gives an overview of hair modelling techniques and

section 3 introduces our wisp based model and an

improved statistical model for hair wisp generation.

Section 4 presents algorithms for fast photo-realistic

rendering using improved data structures and more

efficient GPU algorithms for the light reflection

calculation and shadow generation. Section 5

proposes methods for real-time antialiasing using

GPU programming. Section 6 contains implementa-

tion details and section 7 discusses our results. We

draw conclusions about our research in section 8 and

finish with a listing of future work in section 9.

2 INTERACTIVE HAIR

MODELLING AND STYLING

In order to develop efficient styling tools it is

important to find the most suitable hair model.

Popular approaches are polygonal surfaces,

volumetric textures, and strand-based and wisp-

based models.

Parke introduced a fast and simple way to model

hair which uses simple texture mapped polygonal

surfaces to capture the shape and appearance of hair

(Parke, 1974). Since the surface representation does

not model the complex geometry of hair strands the

specular lighting effects are not correct and the

resulting rendered images lack realism.

In contrast strand-based models represent every hair

strand explicitly either by thin cylinders, which are

slow to render and suffer from aliasing artefacts, or

204

(Ray) Zhang R. and C. Wünsche B. (2007).

A FRAMEWORK FOR INTERACTIVE GPU-SUPPORTED RENDERING AND STYLING OF VIRTUAL HAIR.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - AS/IE, pages 204-211

DOI: 10.5220/0002085602040211

 SciTePress

by using connected line segments (Anjyo, Usami,

and Kurihara, 1992; Rosenblum, Carlson, and Tripp,

1991). This type of model is suitable for simple

styles using long, animated hair, but it is not

practical for creating complex hairstyles due to the

large number of strands which must be moved.

An improvement is achieved by grouping hair

strands into wisps whose shape and movement is

defined by using key strands. The idea is based on

the observation that adjacent hair strands tend to

form wisps due to static attraction and artificial

styling products. Daldegan et al. use a triangular

head mesh and define key hair strands at each

triangle vertex in order to interpolate the wisps’ hair

strands (Daldegan et al., 1993). Yang et al. use

generalized cylinders to represent hair wisps (Yang

et al., 2000). Plante et al. propose an animation

method to deal with the interactions among wisps

and to simulate complex hair motions (Plante et al.,

2001). The above three models have the advantage

that they make it easy to control hair styling.

However, the methods are not effective for

controlling complex hairstyles such as curly hair.

In 2002 Kim and Neumann proposed a multi-

resolution hair modelling system, which can handle

fairly complex hairstyles (Kim and Neumann, 2002).

The model makes it possible to define the behaviour

of hair over the entire range from hair wisps down to

individual hair strands. Different hair styles can be

created rapidly using high-level editing tools such as

curling, scaling and copy/paste operations.

Subsequently Choe and Ko introduced a statistical

wisp model to generate a wide range of human

hairstyles (Choe and Ko, 2005). The authors

simulate hair deformation by applying physical

properties of hair such as gravity and collisions

response. The model is capable of handling a wide

range of human hair styles but is unsuitable for

simulating hair animation due to a lack of real-time

performance of their modelling algorithm and failing

in collision detection in some cases.

Other models have been proposed such as

volumetric textures for modelling fur and short hair

styles (Perlin, 1989; Kajiya and Kay, 1989) and

particle-based hair models, which simulate hair

strands as trajectories of particles shot from the head

(Stam, 1995).

In conclusion wisp-based models are the most

flexible hair models since they support high-level

operations such as copy/paste between wisps when

designing a hair style, but also give control about

details of a hair style. Disadvantages of this

approach are the large amount of time needed to

handle the interactions between hair strands such as

collision detection and difficulties in simulating

convincing hair animation. However, for many

applications with little animation, such as hair

styling, the advantages outweigh the disadvantages,

and we therefore use a wisp-based model.

3 STYLING TOOLS

Our hair model is based on the static wisp-based

model proposed by Choe and Ko (2005). Hair

strands are placed on a high resolution triangle mesh

head model shown in figure 1.

Figure 1: A head model represented by a triangle mesh.

The scalp region is coloured brown.

Inspired by Kim and Neumann’s interactive

hair modelling system (Kim and Neumann, 2002)

we added tools to enable users to manipulate wisps.

Since a scalp can have tens of thousands of hair

strands we need a system to easily control groups of

hair strands. The user is able to group several

triangles on which to grow a wisp. The size (number

of strands) of a wisp is dependent on the area of

selected triangles. The smallest wisp is defined by a

single triangle. This level of detail is sufficient for

defining a wide variety of hair styles since the

triangles are small compared to the scalp’s area.

The geometry of a wisp is controlled using a key

strand as illustrated in figure 2. The key strand

defines the geometry for all strands of a wisp which

are then obtained by translating them as described in

subsection 3.2. We use Catmull-Rom splines

(Catmull and Rom, 1974) to represent hair strands

since they are smooth (C

continuous) and because

they interpolate their control points which makes

designing a particular hair style more intuitive.

A FRAMEWORK FOR INTERACTIVE GPU-SUPPORTED RENDERING AND STYLING OF VIRTUAL HAIR

205

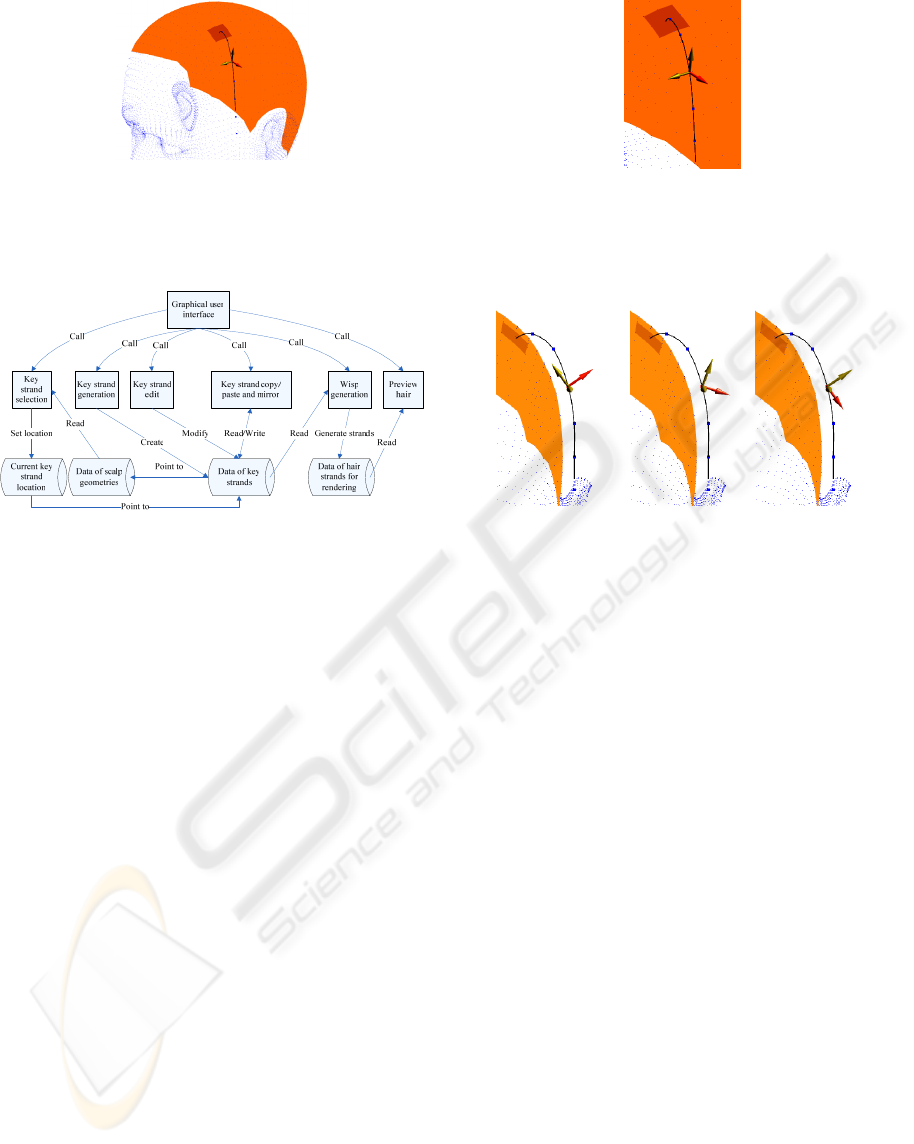
Figure 2: A key strand defining a wisp for a group of four

triangles on the scalp. The dark area on the scalp defines

the selected triangles. The blue square points are the

control points on the key strand.

Figure 3: An overview of the components of our hair

styling toolset.

The components of our hair styling toolset are

illustrated in figure 3. The key strand selection

component enables users to choose triangles to grow

a wisp or to select an existing wisp for editing. After

a group of triangles has been selected it is recorded

together with the location of its current key strand.

The location of the key strand is determined as the

centre of the first triangle of the selected group of

triangles (see section 3). The selection of scalp

triangles and strand control points has been

implemented with the OpenGL “select” mechanism.

This enables us to detect whether the projection of a

graphical primitive onto the view plane overlaps

with a hit region surrounding the mouse location in

which case we select the front most primitive.

3.1 Key Strand Control

Users are able to interactively modify a key strand

by adding, deleting and moving control points. The

interface for changing the 3D coordinates of the

control points of a key strand is illustrated in figure

4. Since the mouse movements on the screen are in

2D we have to map this into a suitable 3D motion. A

common solution in modelling applications is to

restrict movements to the coordinate directions,

parallel to the view plane or within a user defined

plane.

Figure 4: The user interface for changing the 3D positions

of a key strand’s control points. The red arrow indicates

the currently active direction in which the control point

can move forward and backward. The yellow arrows

indicate the non-active directions.

Figure 5: Rotation of the local coordinate system at a

control point.

We found that in hair styling the preferred hair

movement direction depends on a particular style,

e.g. “brushing” hair backwards, lifting it up, pulling

it down or curling it. We therefore define for each

key strand a local coordinate system of styling

directions represented by three orthogonal arrows.

The currently active styling direction is indicated by

a red arrow. A new styling direction is obtained by

choosing one of the non-active arrows or by

changing the local coordinate systems as illustrated

in figure 5.

Suitable default directions for the local

coordinate system at a control point are the curve

tangent at that point, the surface normal at the scalp

point closest to the control point and the vector

perpendicular to these two vectors.

3.2 Wisp Control

Users can change the size of a wisp by changing the

triangles defining the area on which the strands of

this wisp grow. High-level copy/paste and mirror

operations between wisps are provided by the key

strand copy/paste and mirror component. After

selecting the triangles for a wisp, the geometry of a

key strand can be copied or mirrored from an

existing wisp to a new one as illustrated in figure 6.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

206

The source wisp

The mirrored wisp

Figure 6: The red key strand in the right image is a mirror

version of the key strand in the left image.

The wisp generation component is able to

generate all hair strands determined by their key

strands and to distribute all hair strands over the

scalp uniformly based on the hair density specified

for different scalp regions.

The hair strands within a wisp tend to be similar,

although some variations are required to improve

realism. Choe and Ko observed that the degree of

similarity can be controlled by a length distribution,

radius distribution and strand variation (Choe and

Ko, 2005). The length distribution determines the

length variance between the key strand and a

member strand within a wisp. The radius distribution

controls the distance between the key strand and a

member strand within a wisp. Finally the strand

distribution gives the shape variation of each strand

compared to the key strand.

Rather than varying the position of each control

point of a member strand with respect to the key

strand (Choe and Ko, 2005) we define for each

control point an offset vector which linearly

increases in length for each subsequent control

point. The initial offset vector is randomly selected

using a uniform distribution over a sphere. In order

to maintain the overall shape of the strand the offset

vector is defined with respect to a torsion

minimising reference frame for the spline curve

representing the strand (Bloomenthal, 1990).

Figure 7 illustrates this process. The key strand

on the right is reproduced at the new root position.

We then define a random offset vector for the first

control point subject to a maximum length indicated

by the circle in the figure. The offset vector’s length

linearly increases for subsequent control points.

Applying it with respect to the key strand’s

reference frame generates a new curve of similar

appearance. We also implemented a strand

distribution but found that the hair styles using it

were indistinguishable from the ones using just

length and distance variations.

Figure 7: The original key strand (left) and the resulting

member strand (right).

4 RENDERING ALGORITHMS

We have developed two rendering algorithms which

take advantage of new GPU functionalities in order

to render hair realistically in real-time. Both

algorithms implement an anisotropic reflection

model for the illumination of hair strands (Kajiya

and Kay, 1989) and use opacity shadow maps (Kim

and Neumann, 2001) for simulating self-shadowing.

The algorithms differ in terms of data structures and

utilised GPU features. More details are described in

the implementation section and a comparison and

evaluation is given in the result section.

5 ANTIALIASING

Because hairs are very fine structures with a width

and inter-hair distance of equal or below the image

pixel size, rendering hair can result in aliasing

artefacts. While increasing the sampling frequency

would help this is not an option when interactive

performance is required and we have to employ

instead antialiasing techniques which can be

grouped into three approaches: prefiltering,

supersampling, and postfiltering.

Prefiltering is the best way to perform

antialiasing because it removes high frequencies in

the view of a scene before rendering an image. This

can be achieved by calculating for each rendered

primitive its coverage of an image pixel. If the

coverage is below 100% the values for all primitives

contributing to that pixel are averaged. Analytical

prefiltering removes high frequencies of the

intensity function representing the image by using

mathematical operators (Chan and Durand, F.,

2005). Supersampling uses an increased sampling

frequency. High frequency components are removed

using a low pass filter (e.g. a box filter), before

down-sampling the image to the required size.

A FRAMEWORK FOR INTERACTIVE GPU-SUPPORTED RENDERING AND STYLING OF VIRTUAL HAIR

207

Postfiltering also uses convolution kernels, but

operates directly on the final resolution image.

Our hair rendering antialiasing implementation is

based on supersampling and postfiltering techniques

implemented on the GPU and is described in more

detail in the next section.

6 IMPLEMENTATION

6.1 Rendering Algorithms

We have implemented two rendering algorithms

which both have three components: data preparation,

which converts data into the required format and

loads it into memory, opacity shadow maps (OSM)

generation and hair rendering.

Figure 8: Overview of the first rendering algorithm.

Figure 8 illustrates our first implementation

which uses vertex buffer objects to store hair data as

OpenGL server side objects on the graphics card.

The GPU can access the vertex buffer objects

directly without transferring the data set from the

CPU. Opacity shadow maps are created from the

vertex buffer objects by rendering the hair geometry

using the light position as view point. The fragment

shader outputs the opacity value sequentially to the

frame buffer through the fixed function pipeline of

OpenGL by using the Multiple Render Targets

technology which allows a fragment shader to write

to up to four buffers within the frame buffer.

Sixteen maps can be generated in one rendering pass

as we store up to four maps in four channels of each

buffer.

Hair strands are rendered using vertex shaders

which implement an anisotropic reflection model

(Kajiya and Kay, 1989) to compute the correct

illumination at the polylines’ vertices. The fixed

OpenGL functionalities interpolate the colour values

and then pass the values to the fragment shader. The

shader computes the opacity value of each strand’s

incoming fragment by linearly interpolating the two

adjacent shadow maps loaded from the GPU texture

memory (Koster, Haber and Seidel, 2004). We use

the following fast interpolation function which

avoids branch statements for searching (Nguyen and

Donnelly, 2005):

])/||1,0max(*[

∑

−

−−Ω=Ω

dzzz

(1)

is the opacity value of a point,

Ω is the

corresponding opacity value on the i

map, n is the

total number of maps,

z is the distance of i

map

from the light position,

z is the distance of the point

from the light position, and

dz is the distance

between two adjacent maps using the assumption

that all the distances between maps are equal. We

have proven the validity of this formula (

Anonymous,

2006

Figure 9: Overview of the second rendering algorithm.

The second rendering algorithm, outlined in

figure 9, uses two OpenGL contexts with copies of

the hair data in order to make use of the render-to-

texture technology: one copy is for the opacity

shadow map generation and one for the hair

rendering. The render-to-texture technology is

currently the only way in GPU programming to

enable a fragment shader to output data directly to

the texture memory on the GPU. Hence this is the

fastest way to put the data of the opacity shadow

maps into the texture memory. The OSM is

generated as for the first implementation, except that

the fragment shader outputs the data directly into the

texture memory.

The advantage of the first implementation is that

it always runs in the same OpenGL context, i.e. no

expensive OpenGL context switching is required.

Drawbacks are the cost of copying data from the

frame buffer to the texture memory and that it

requires more powerful GPUs which offer multiple

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

208

render targets. In addition the sample rate of the

shadow maps is fixed to the screen resolution of the

OpenGL context. The second implementation is

more widely supported by graphics hardware.

However, the cost for OpenGL context switching is

high and the amount of memory consumed is almost

1.4 times as large as for the first implementation.

6.2 Antialiasing

Postfiltering is performed by copying the rendered

image from the frame buffer to the texture memory

in the GPU. Fast processing is achieved by using a

fragment shader which averages pixel values

according to the selected convolution kernel. The

resulting colour of the fragment is processed by the

fixed functionality OpenGL pipeline and written to

the frame buffer. We restrict processing of

fragments to the minimal quadrilateral covering the

hair region since skin and other scene objects don’t

have the same fine structures as hair.

Supersampling is similar to postfiltering but

differs in three points: (a) We need to adjust the

OpenGL context to a larger screen size in order to

accommodate the high resolution supersampled

image. The highest possible resolution is depended

on the capability of the graphics hardware. (b) We

use the “render-to-texture” capability of modern

GPUs to render to the texture memory of the GPU

directly instead of copying the data back from the

frame buffer to the texture memory. (c) In order to

apply the convolution kernel to the incoming

fragment we need to find the texture coordinates of

all the neighbour pixels required by the kernel. The

texture coordinates can be computed by considering

the ratio between the supersampling resolution and

the rendering resolution.

7 RESULTS

7.1 Effectiveness

Our hair styling toolset is capable of creating a

variety of moderately complex styles. Depending on

the complexity of a new hair style it can take up to

several hours for a user without modelling

experience to create it. Adjusting the key strands is

the most time consuming step when making a

specific style. Two examples of completed hair

styles created by us are shown in figure 10. Our hair

styling toolset can model and render real hair styles

effectively as demonstrated in figure 11. Shadow

effects in hair volumes are compared in figure 12.

We tested our tool with non-expert users and

found that most functions such as wisp copy/paste,

mirror, and preview are quite intuitive. However

users found that they need to explicitly design the

wisp interactions and it is a little bit difficult to

define the directions of key strands. The current

version of our toolkit does not perform collision

detection between strands and wisps and does not

use an explicit physical model and it is therefore

difficult to model braided hairstyles.

Figure 10: A curly short hair style (left) and a smooth

medium length hair style (right).

Figure 11: A real (left) and a computer generated hair

style (right).

The image on the left of figure 13 demonstrates that

the distribution function by Choe and Ko, which

uses random offsets for control points, can lead to

slightly wavy strands even if the original key strand

is uniformly curved. In contrast our function

produces uniformly smooth wisps. Furthermore by

defining the maximum length of the initial offset

vector we can produce very smooth hair where the

strands are virtually parallel and very fuzzy hair

where the distance between hair strands increases at

the end of a wisp.

A FRAMEWORK FOR INTERACTIVE GPU-SUPPORTED RENDERING AND STYLING OF VIRTUAL HAIR

209

Figure 12: A hair volume without shadow (left) and with

shadow (right).

Figure 13: A large wisp generated with Choe and Ko’s

distribution function (left) and with our function (right).

Note that the results were exaggerated by using large

offset vectors in order to emphasize the differences

between the methods.

7.2 Efficiency

We implemented our algorithms using C/C++ and

OpenGL and run them on a PC with 2GB memory, a

2 GHz Intel Pentium M Processor 760 and an

NVIDIA GeForce Go 7800 GTX graphics card with

256 MB memory. We found that the speed of our

GPU-based anisotropic reflection algorithm is

almost ten times as fast as for the equivalent CPU

implementation (Anonymous, 2006). The complete

algorithms including opacity shadow maps can

render a head model with 16,215 hair strands

(357,267 line segments) with 13-20 frames/second.

7.3 Antialiasing

We implemented GPU-based box filter and

Gaussian filter kernels and found that they are able

to partially solve the aliasing problem as illustrated

in the images 2 and 3 of figure 14. We found that

two times hardware build-in supersampling with and

without Gaussian filtering (image 5 and 6 of figure

14, respectively) yields the best antialiasing results.

Note that the images show different hair regions, but

in this subsection we are only interested in the

appearance of individual hairs on skin so that this

does not matter.

(1) Aliasing

(2) Box filter

(3) Gaussian filter

(4) 2X supersampling(GPU)

(5) 2X supersampling

(Hardware build-in) and

Gaussian filter

(6) 2X supersampling

(Hardware build-in)

Figure 14: Results obtained with different antialiasing

techniques.

The performance of all antialiasing schemes is

satisfactory and increases total rendering time

between 17% (box filter) and 34.2% (2x hardware

built-in supersampling and Gaussian filter).

8 CONCLUSIONS

Although the hair styling process can require a

couple of hours we found that our toolset enables

users to create a variety of hair styles efficiently and

effectively. The toolset provides not only high-level

functionality such as copy/paste and mirroring of

wisps, but also low-level modifications such as

changing the number and positions of a key strand’s

control points in order to modify the shape of a wisp.

This was achieved using a novel interaction tool

which uses a local-coordinate system for defining

“styling directions”.

We have introduced a new statistical method to

generate strands from a key strand which has the

advantage that it maintains consistency of style

within a wisp and that it enables users to model

smooth, fuzzy and fringy hair. With our density

based hair distribution facility the roots of hair

strands are distributed evenly over the scalp.

Rendering is performed in real-time using GPU

accelerated algorithms and the whole modelling

process is interactive.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

210

9 FUTURE WORK

Much work remains to be done in order to make our

model suitable for a wider range of applications.

Hair dynamics must be implemented in order to use

our model for animations where the hair moves

dynamically with the body motion or through

outside forces such as wind. We believe an

interesting approach for interactive environments is

to create a global deformation field for the hair

volume rather than modelling the motion of

individual wisps. We would also like to improve the

styling toolset to incorporate constrained hair styles

such as ponytails and braided styles.

REFERENCES

Anjyo, K., Usami, Y., Kurihara, T., 1992. A simple

method for extracting the natural beauty of hair.

SIGGRAPH '92: Proceedings of the 19th annual

conference on Computer graphics and interactive

techniques, ACM Press, New York, NY, USA, pp.

111-120, 1992.

Anonymous, 2006, details deleted for this review.

Bloomenthal, J., 1990. Calculation of reference frames

along a space curve. Graphics Gems Vol. 1, Academic

Press, San Diego, CA, USA, 1990, pp. 567-571.

Catmull, E., Rom, R., 1974. A Class of Local Interpolating

Splines. Computer Aided Geometric Design, R. E.

Barnhill and R.F. Riesenfeld ed., Academic Press,

New York, 1974, pp. 317-326.

Chan, E., Durand, F., 2005. Fast Prefiltered Lines. GPU

Gems 2, Addison-Wesley, Boston, MA, USA, March

2005, pp. 345-359.

Choe, B., Ko, H., 2005. A statistical Wisp Model and

Pseudophysical Approaches for Interactive Hairstyle

Generation. IEEE Transactions on Visualization and

Computer Graphics, vol. 11, no. 2, pp. 160-170, Mar-

Apr 2005.

Daldegan, A., Thalmann, N. M., Kurihara, T., Thalmann,

D., 1993. An integrated system for modelling,

animating, and rendering hair. Proceedings of

Eurographics, vol. 12, pp. 211-221, 1993.

Kajiya, J.T., Kay, T.L., 1989. Rendering Fur with Three

Dimensional Textures. SIGGRAPH Proceedings, vol.

23, pp. 271-280, July 1989.

Kim, T., Neumann, U., 2001. Opacity Shadow Maps.

SIGGRAPH '02: Proceedings of the 12th Eurographics

Workshop Rendering, June 2001, pp. 177-182.

Kim, T., Neumann, U., 2002. Interactive multiresolution

hair modelling and editing. SIGGRAPH '02:

Proceedings of the 29th annual conference on

Computer graphics and interactive techniques, ACM

Press, New York, NY, USA, pp. 620–629, July 2002.

Koster, M., Haber, J., Seidel, H., 2004. Real-Time

Rendering of Human Hair using Programmable

Graphics Hardware. Proceedings of Computer

Graphics International, 2004, pp. 248-256.

Lafrance, M., 2005. First Impressions and Hair

Impressions. Unpublished manuscript, Department of

Psychology, Yale University, New Haven,

Connecticut. http://www.physique.com/sn/sn_yale-

study2.asp, visited on 15th July 2005.

Nguyen, H., Donnelly, W., 2005. Hair Animation and

Rendering in the Nalu Demo. GPU Gems 2, Addison-

Wesley, Boston, MA, USA, March 2005, pp. 361-380.

Parke, F. I., 1974. A Parametric Model for Human Faces.

Unpublished manuscript, PhD thesis, University of

Utah, Salt Lake City, UT, UTEC-CSc-75-047,

December 1974.

Perlin, K., 1989. Hypertexture, SIGGRAPH Proceedings,

vol. 23, pp. 253-262, 1989.

Plante, E., Cani, M. P., Poulin, P., Perlin, K., 2001. A

layered wisp model for simulating interactions inside

long hair. Proceedings of Eurographics Computer

Animation and Simulation 2001, pp. 139-148, Sep

2001.

Rosenblum, R., Carlson, W., Tripp III, E., 1991.

Simulating the structure and dynamics of human hair:

Modelling, rendering and animation

. The Journal of

Visualization and Computer Animation, vol. 2, no. 4,

pp. 141-148, October-December 1991.

Stam, J., 1995. Multi-Scale Stochastic Modelling of

Complex Natural Phenomena. PhD Thesis, Dept. of

Computer Science, University of Toronto.

Yang, X. D., Xu, Z., Yang, J., Wang, T., 2000. The

Cluster Hair Mode. Graphical Models, vol. 62, pp. 85-

103, 2000.

A FRAMEWORK FOR INTERACTIVE GPU-SUPPORTED RENDERING AND STYLING OF VIRTUAL HAIR

211