A NOVEL DYNAMIC GREEDYDUAL-SIZE REPLACEMENT

STRATEGY TO MAKE TIME-CRITICAL WEB APPLICATIONS

SUCCESSFUL

Allan K. Y. Wong, Jackei H. K.Wong, Wilfred W. K. Lin

Department of Computing, Hong Kong Polytechnic University, Hong Kong SAR

Tharam S. Dillon

Digital Ecosystems and Business Intelligence Institute, Curtin University of Technology, Australia

Keywords: Dynamic GreedyDual-Size, dynamic cache size tuning, hit ratio, time-critical web applications.

Abstract: The GreedyDual-Size (GD-Size) replacement algorithm is a static-cache-size approach that yields a higher

hit r

atio than the basic LRU replacement algorithm. Yet, maintaining a given hit ratio needs dynamic cache

size tuning, and this can only be achieved by the MACSC (model for adaptive cache size control) model so

far. Since the GD-Size yields a higher hit ratio than the basic LRU, it is proposed in this paper to replace the

LRU unit in MACSC with the GD-Size algorithm. The replacement creates a new and more efficient

dynamic cache size tuner, Dynamic GreedyDual-Size (DGD-Size).

1 INTRODUCTION

In this paper mobile business (m-business) is used as

an example to show how caching is related to time-

critical web application success. M-businesses

involve e-shops operating on the mobile Internet,

and the key issue is how to galvanize customers

quickly within their short attention spans (Venkatesh

2003). In fact, the galvanization power depends on

consistent short client/server service roundtrip time

(RTT). This power can be magnified by techniques.

Caching performance generally ties in with the

cache hit ratio, higher t

he better. Although

conventional caching strategies (Podlipnig 2003)

may produce high hit ratios, they cannot maintain

them because they work with a fixed-size cache. In

contrast, the novel dynamic GreedyDual-Size

(DGD-Size) replacement strategy proposed in this

paper works with a variable cache size, which is

adjusted adaptively on the fly. The DGD-Size

strategy normally maintains a hit ratio higher than

the given one. For this reason it is tremendously

suitable for time-critical web applications such as m-

businesses and telemedicine setups.

A higher hit ratio (i.e. higher chance of finding

the re

quested object in the proxy cache) means a

shorter RTT because it reduces the need for cyber

foraging (Garlan 2002). If the proxy server cannot

find the requested object in its local cache, it has to

enlist help from other remote data sources (e.g.

collaborating nodes, proxies, or web servers over the

Internet). This enlisting process is cyber foraging,

which involves the Internet domain name server

(DNS) and thus a longer delay. Let us visualize this

delay in terms of a m-business setup, which normally

has two phases: mobile commerce (m-commerce)

and electronic commerce (e-commerce).

a) M-commerce focuses on ho

w to galvanize

customers effectively with attractive promotional

material. Via mobile devices (i.e. small-form-factor

(SFF) devices such as PDA and mobile phone) the

customers browse promotions to window-shop

electronically. Some customers may end up buying

goods from different e-shops and have their

transactions handled by the e-commerce phase. In m-

business, service RTT has two meanings: M-

commerce service RTT for promotional purposes:

This occurs between the customer and the “m-

commerce hub”, which is modeled as a proxy server

in Figure 1. This service RTT is the “first-leg” delay

in m-business.

K. Y. Wong A., H. K.Wong J., W. K. Lin W. and S. Dillon T. (2007).

A NOVEL DYNAMIC GREEDYDUAL-SIZE REPLACEMENT STRATEGY TO MAKE TIME-CRITICAL WEB APPLICATIONS SUCCESSFUL.

In Proceedings of the Second International Conference on e-Business, pages 17-22

DOI: 10.5220/0002106800170022

 SciTePress

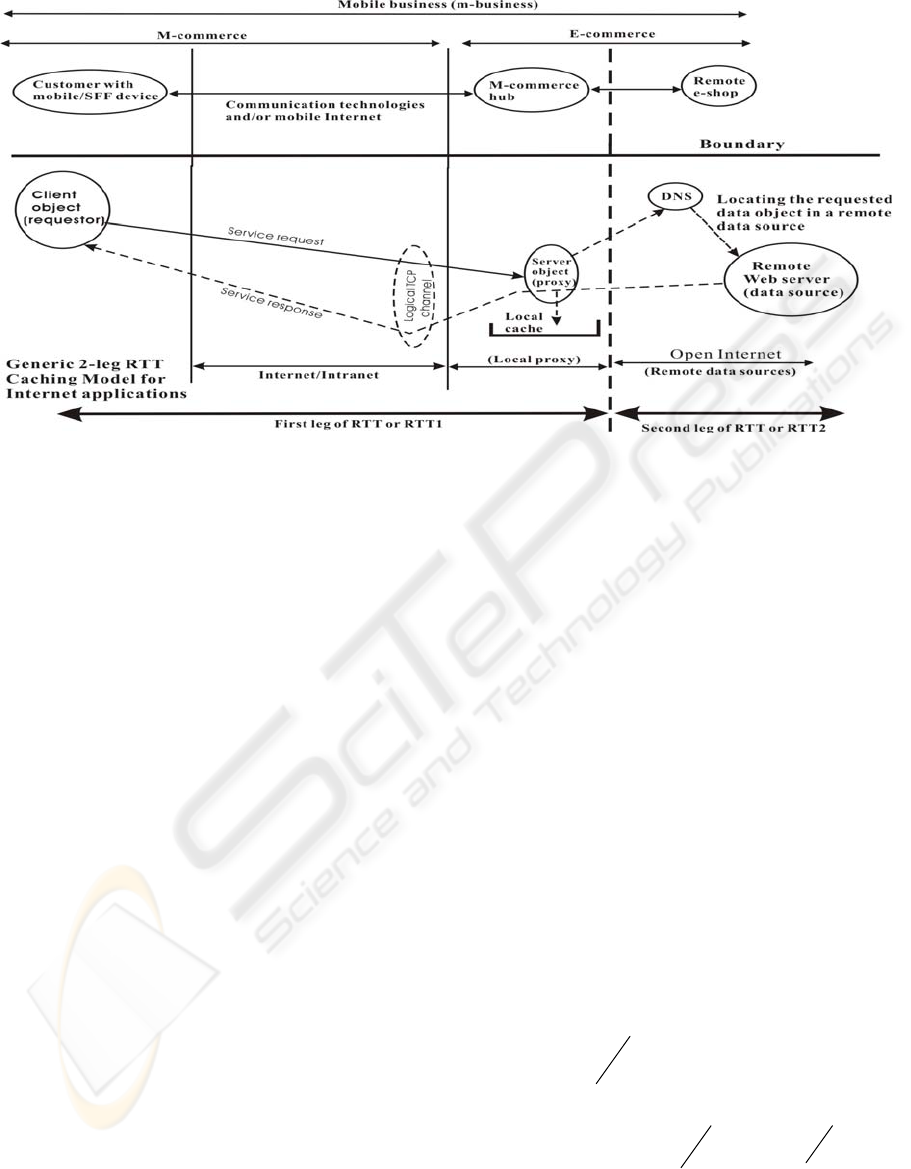
Figure 1: The two legs in the service RTT of a caching system.

b) E-commerce service RTT for transactional

purpose: This is the delay between the proxy server

and the e-shop, modeled as the remote e-shop in

Figure 1. This is the transaction-oriented “second-

leg” interaction in m-business.

To summarize, a complete m-business venture

should have two “legs” of service delays. If the

customer only window-shops electronically, solely

the first leg is involved. If an e-shop is involved (e.g.

checking details of the goods or paying

electronically), the second leg is also needed.

In reality, the m-commerce hub is an e-trading

(electronic trading) platform/firm, which charges a

fee for completing electronic transactions. For

effective promotional purposes the firm would

gather adverts of popular goods from different e-

shops and cache them to function like an electronic

catalogue. Then, the customers can browse these

adverts without the need to go directly to the e-

shops. Since only the first-leg delay is present, the

response is much faster. How the adverts are

selected, endorsed and organized is a matter of

business policy. For example, the successful

Japanese NTT DoCoMo i-mode (information mode)

m-business setup, which operates over the mobile

Internet by packet switching, maintains a list of e-

shops endorsed by the company with stringent

criteria.

The lower half (under the boundary) of Figure 1

models the generic 2-leg RTT for web applications.

The upper half describes how the m-business

operations fit into this generic model. The generic

proxy server represents the m-commerce hub, which

caches and manages the popular adverts

(descriptions of the goods including places of origin,

prices, and functions) as data objects. Customers

browse these data objects via mobile or SFF devices

(i.e. the first-leg RTT). When a customer buys goods

from the e-shops, it is the e-commerce phase (i.e. the

RTT second-leg in Figure 1) that handles the

electronic transactions of legal implications

2 RELATED WORK

Caching provides two main advantages as follows:

a) Shortening the service RTT between the client

and server: This is achieved because the cache hit

ratio

reduces the involvement of the “second leg”

or leg-2 operation (Figure 1). For illustration

purposes let us assume:

8.0

, T as the average

service RTT for the “first leg” or leg-1 operation,

10T as the average service RTT for leg-2 operation

(due to the remoteness of the external data sources

such as web servers), and as the speedup due to

caching. Then, the speedup is

]10*)1([

)10(

−+

= , where

)1(

−

is the miss ratio. With the assumption

above is equal to

S 7.3

)21(

≈=

+ T

fold. The speedup ratio increases with

and is

independent of T.

ICE-B 2007 - International Conference on e-Business

b) Reducing the physical RTT: Since the number

of data objects to be transferred across the network

is reduced by caching, more backbone bandwidth is

automatically freed for public sharing. As a result

less chance of network congestion reduces the T

value above as a fringe benefit.

Our literature search indicates that researchers

are incessantly trying to find effective caching

techniques to achieve the following:

a) Yielding a high

without deleterious effects:

The solution computation must be optimal in a real-

time sense. That is, this solution should be ready

before the problem has disappeared. Otherwise, the

solution would correct a spurious problem and

inadvertently lead to undesirable side effects (i.e.

deleterious effects) that cause system instability or

failure. The survey in (Wang 1999) presented the

various ways (deployed and experimental) whereby

can be enhanced. But, the most researched topic

is replacement algorithms, which decide which

objects in the cache should be evicted first to make

room for the newcomers.

b) Maintaining

on the fly: This school of thought

is called dynamic cache size tuning (Wu 2004), and

the only published model, which works with a

variable cache size, is the MACSC (Model for

Adaptive Cache Size Control (Wong 2003). In

contrast, other extant dynamic caching techniques

work with a static/fixed cache size; they may yield a

high hit ratio but do not maintain it.

2.1 Replacement Algorithm

Some researchers compared the hit ratios by

different replacement algorithms that work with a

static cache size by trace-driven simulations (Cao

1997, Wasf 1996, Asawf 1995); LRU (least

frequently used), LFU (least frequently used), Size

(Williams 1996), LRU-Threshold, Log(Size)+LRU,

Hyper-G, Pitkow/Recker, Lowest Latency First,

Hybrid (Wooster 1997), and LRV (lowest relative

value). The simulations showed that the following

five consistently produce the highest hit ratios: a)

LRU (least frequently used), b) Size, c) Hybrid, d)

LRV (lowest relative value) and (e) GreedyDual-

Size (or GD-Size). The GD-Size yielded the highest

hit ratio of them all, but its hit ratio can dip suddenly

because of the fixed-size cache, which cannot store

enough data objects to maintain a high hit ratio. So

far, the only known model for dynamic cache size

tuning from the literature is the MACSC [Wong

2003]. All the available MACSC performance data,

however, was produced together with the basic LRU

replacement algorithm as a component. In effect, the

MACSC makes the LRU mechanism adaptive for

MACSC adjusts the cache size on the fly; the cache

size is now a variable. Since the previous experience

(Cao 1997) had confirmed that the GD-Size

algorithm yields a higher hit ratio than LRU, it is

logical to combine MACSC and GD-Size to create

an even more efficient caching framework. This

combination, which is proposed in this paper, creates

the novel dynamic GD-Size (DGD-Size)

replacement strategy. The DGD-Size should be able

to maintain a higher hit ratio than the previous LRU-

based MACSC’s.

2.2 The MACSC Concept

Figure 2 shows the popularity profile over time for

the same set of data objects. The A, B and C curves

represent the three instances of the profile changes.

These instances were caused by changes in user

preference towards certain data objects. Any such

change is reflected by the current profile standard

deviation, for example, SD

, SD

and SDB

. From

the perspective of a changeable popularity spread,

any replacement algorithm designed to gain a high

hit ratio with a fixed-size cache

works well only

for

≤

∇

. That is, the cache size

∇L

accommodates the given hit ratio equal to L

times the standard deviation

∇

of the data object

popularity profile. If the expected hit ratio is for

(i.e. 68.3%), then the cache size is

initialized accordingly. In the MACSC case,

S is

continuously adjusted with respect to the current

relative data object popularity profile on the fly.

Conceptually,

CL∇

always holds;

is the

adjusted cache size at time t. From two successive

measured standard deviation values the MACSC

computes the popularity ratio (PR) for tuning the

cache size. The PR is also called the standard

deviation ratio (SR) as shown by equation (2.1),

where

is the new cache size adjustment and

the current SR is inside the brackets.

SS ≤ S

Figure 2: Spread changes of the relative data object

popularity profile over time.

)1.2...(*

⎟

⎠

⎞

⎜

⎝

⎛

∇

−−

profilepopularityLast

profilepopularityThis

SROldSR

CSCS

A NOVEL DYNAMIC GREEDYDUAL-SIZE REPLACEMENT STRATEGY TO MAKE TIME-CRITICAL WEB

APPLICATIONS SUCCESSFUL

Conceptually the MACSC should predict the

true/ideal mean

and the true/ideal standard

deviation

of the current popularity profile for

equation (2.2). In practice it is rare that the exact

values for

and

can be computed statistically.

To differentiate

and

from their estimated

values by the MACSC mechanism the following are

defined:

a) Estimated mean ( x ): This is calculated for a

sample of arbitrary size n, and the minimum value

for n should be greater than 10 or .

10≥n

b) Estimated standard deviation s

: This is

calculated from the same n data points above. In the

MACSC operation the finally settled s

is the

∇

value in equation (2.1) (i.e. accepted measurement

for the specified error tolerance).

is the measured standard deviation for the

curve plotted with a collection of

x values (i.e.

means of different

samples), by the central limit

theorem the relationship (2.2) holds, provided that n

is large enough and there is a sufficient number of

values. The estimated s

for every sample of size n

usually differs from

. Since estimating the

acceptable mean and the standard deviation of an

unknown distribution is a guessing game, it is

necessary to set a reasonable error tolerance. By

assuming the following tolerance parameters the

“

equationN − ” (2.3) can be derived [Chis92]:

a) Error tolerance E: It is the fractional/percentage

error about

(ideal/true mean) by the estimated

mean

x for a sample of n data points (i.e.

variables) collected on the fly.

b) The tolerance k: It is the number of standard

deviations that

x is away from the true mean

and

still be tolerated (E and k connote same error).

3 THE DYNAMIC

GREEDY-DUAL SIZE

FRAMEWORK

The dynamic GreedyDual-Size (DGD-Size)

conceptual framework has two basic parallel tasks:

a) P1 - the original static GreedyDual-Size (GDS)

mechanism, and b) P2 - the MACSC dynamic cache

size tuner. P1 computes the utility of every newly

cached/accessed data object. If there is not enough

space to cache a new object, the object(s) in the

cache with the lowest utility

min

U will be evicted

one by one until enough space is made available. In

every eviction cycle the utilities of all the extant

objects are reduced by the current

min

U , as shown

by “step 2” of P1. The utility of an object is

recomputed when it is accessed. The parallel task P2

samples data points on the fly to capture the current

relative object popularity profile for the cache

[Wong03]. With these data points MACSC

computes the popularity ratio and the current cache

size adjustment

CS to maintain the given hit ratio.

In fact, P1 works with the current by P2 in a

transparent manner.

Par (P1 and P2): /* P1 and P2 are 2 parallel

tasks of Dynamic GreedyDual-Size */

{ P1:

step 1:

zdcpodU )()(

;

/* To computes the utility U(d) of

every newly cached/accessed object */

step 2: While (not enough cache space)

do { /* Evict object of lowest utility

and the utilities of all cached

objects minus */

min

Evict ( );

min

)()( UdUdU −

}

} /* End P1 –DGS mechanism */

P2:

{

} /* End P2 - dynamic cache tuning */

} /* end of DGD-Size domain*/

Figure 3: DGD-Size pseudo-program.

)2.2...(

)3.2)..((

kkE

δμ

4 EXPERIMENTAL RESULTS

Many experiments were performed to verify that the

novel DGD-Size framework (also referred to as the

EMCGDS - our research code name for the

“MACSC + GreedyDual-Size” implementation) can

really achieve the following:

⎟

⎠

⎞

⎜

⎝

⎛

∇

−−

profilepopularityLast

profilepopularityThis

SROldSR

CSCS *

a) Produce and maintain a hit ratio higher than the

given one.

b) Outperform the conventional static GD-Size (or

simply GDS) approach.

c) Outperform the original dynamic “MACSC +

LRU” implementation (customarily called

EMCLRU).

These experiments were carried out on the IBM

Aglets mobile agent platform. The choice of the

platform was intentional because it is designed for

open Internet applications [Aglets], and this makes

the experimental results scalable. The preliminary

ICE-B 2007 - International Conference on e-Business

Caching Comparison

40.00%

45.00%

50.00%

55.00%

60.00%

65.00%

70.00%

75.00%

80.00%

85.00%

90.00%

95.00%

100.00%

b19

BU2 72

Clar knetSep(5)

Cla

rkn

et Aug( 2)

rknet

Se p (

Cla

rkn

et Aug( 4)

Clar

et Aug( 1)

Clar knetSep(1)

rknet

Se p (

ar kn

ug(

Cla

rkn

et Aug( 5)

rknet

Se p (

lgar

ug95(

EMCGDS

results from the experiments collectively indicate

that EMCGDS outperforms EMCLRU even though

the latter never ceased to maintain the given hit ratio

as the minimum. In contrast, the hit ratios produced

by the conventional GDS fluctuated drastically. The

Intel’s VTune Performance Analyzer measures the

execution times of EMCGDS, EMCLRU and GDS

for comparison purposes.

Figure 4 compares the average hit ratios by the

three different caching strategies: EMCDGS,

EMCLRU and GDS. Every point on a curve is the

average hit ratio for the whole data trace or trace

segment. The traces used were downloaded from the

web site [Trace]. A concise explanation of the

different traces marked on the axis is in the sequel:

a) BU-Web-Client: This trace contains records of

the HTTP requests and clients’ behaviour in the

Boston University Computer Science Department.

The time span was from 21 November 1994 to 8

May 1995. Two segments of this trace, namely,

BUb19 and BU272 were used to drive two separate

simulations.

b) Calgary-HTTP: This trace is from the

University of Calgary's Department of Computer

Science WWW server in Alberta, Canada. It covers

the period from 24 October1994 to 11 October 1995.

c) ClarkNet-HTTP: ClarkNet is an Internet service

provider in the Metro Baltimore Washington D.C.

area. This trace was divided into 10 segments as

shown in Figure 6.

d) NASA-HTTP: This trace covers the months of

July and August 1995 and contains the HTTP

requests to the NASA Kennedy Space Center’s

WWW server in Florida. It was divided into 6

segments for different simulations.

e) Saskatchewan-HTTP: This trace contains all

the HTTP requests to thee University of

Saskatchewan's WWW server in Canada.

The conclusion that can be drawn from Figure 4

is that EMCGDS consistently produces and

maintains a higher hit ratio than the given one

standard deviation (i.e. one

∇ or 68.3%). In fact, for

the selected traces (marked on the X-axis) the hit

ratio never fell below 87% for EMCGDS. This is

much better than the EMCLRU for which the hit

ratio oscillates seriously even though it never fell

below 70%. The worst performance is the

conventional static GDS because it works with a

static cache size. In the experiments all the cache

sizes were initialized to 500000 bytes for

comparison purposes.

Time-critical web applications usually need

fast client/server response for success. As indicated

by the results in Figure 4, EMCGDS undoubtedly

shortens the client/server service RTT more

dramatically than EMCLRU. For the same

assumptions made in the “Related Work” section,

the minimum speedup by EMCGDS for the data

]10*)9.01([

)10(

−+

)

NASAAug95(4

)

NA S

Aug95( 3

)

ug95(2

)

NA S

Aug95( 1

)

NA S AJ u l

Data Set

Hit Ratio

EMCLRU

GDS

Figure 4: Average hit ratios by EMCGDS, EMCLRU and GDS (e.g. reference is 68.3%).

A NOVEL DYNAMIC GREEDYDUAL-SIZE REPLACEMENT STRATEGY TO MAKE TIME-CRITICAL WEB

APPLICATIONS SUCCESSFUL

traces used in Figure 4 is 5.5 fold (as shown by the

calculation below) for the minimum hit ratio by

EMCGDS is 90%,

The on-line timing analyses by the Intel’s VTune

Performance Analyzer show the following:

a) The average execution time for the

conventional GDS Java implementation in the

experiments is 980 clock cycles.

b) The intrinsic part of the average execution

time for the MACSC implemented in Java is 23425

clock cycles.

VTune had also confirmed that the average

execution time for the basic LRU’s Java

implementation is 627 clock cycles. For the

EMCGDS and EMCLRU mechanisms the

computation delay mainly comes from MACSC

component, which has to sample the time series for

its operation. The inter-arrival times among data

points in the aggregate determines the delay because

enough data has to be sampled for the current

MSCSC control cycle. The MACSC mechanism

actually runs in parallel with GDS or LRU unit.

5 CONCLUSIONS

The preliminary results in the EMCGDS research

confirm that caching indeed makes time-critical web

applications such as m-business setups successful. In

particular, the dynamic caching size tuning

technique contributes to maintain the given cache hit

ratio as the minimum. This shortens the data

retrieval roundtrip time over the Internet in a

consistent fashion. As a result fast system response

makes m-business customers happy and return for

more business. In this light, the DGD-Size

contribution is significant. The next step in the

research is to validate EMCGDS in more open m-

business environments over the mobile Internet.

ACKNOWLEDGEMENTS

The authors thank the Hong Kong Polytechnic

University for the ZW93 research grant and Mr.

Frank Chan’s help in the data collection process.

REFERENCES

M. Abrams, C.R. Standbridge, G. Abdulla, S. Williams

and E.A. Fox, Caching Proxies: Limitations and

Potentials, www-4 Boston Conference, December

1995

C. Aggarwal, J.L. Wolf and Philip S. Yu, Caching on the

Word Wide Web, IEEE Transactions on Knowledge

and Data Engineering, 11(1), 1999

P. Cao and S. Irani, Cost-Aware WWW Proxy Caching

Algorithms, Proc. of the 1997 USENIX Symposium

on Internet Technology and Systems, 1997

J.A. Chisman, Introduction to Simulation and Modeling

Using GPSS/PC, Prentice Hall, 1992

D. Garlan, D.P. Siewiorek, A. Smailagic and P. Steenkiste,

Project Aura: Toward Distraction-free Pervasive

Computing, IEEE Pervasive Computing, 1(2), April

2002, 22-31

O. Mitsuru and K. Guenter, IBM Aglets Specification,

www.trl.ibm.com/aglets/spec11.htm

[Trace] http://ita.ee.lbl.gov/html/traces.html

V. Venkatesh, V. Ramesh and A.P. Massey,

Understanding Usability in Mobile Commerce,

Communications of the ACM, 46(12), December 2003,

53-56

Wang, A Survey of Web Caching Schemes for the Internet,

ASM SIGCOMM, 29(5), 1999

Richard S. L. Wu, Allan K. Y. Wong and Tharam S.

Dillon, RDCT: A Novel Reconfigurable Dynamic

Cache Tuner to Shorten Information Retrieval Time

over the Internet, International Journal of Computer

Systems Science & Engineering, 19(6), 2004

R. Wooster and M. Abrams, Proxy Caching the Estimates

of Page Load Delays, the 6th International World

Wide Web Conference, 1997

S. Williams, M. Abrams, C.R. Standridge, G. Abdulla and

E.A. Fox, Removal Policies in Network Caches for

World-Wide Web Documents, Proc. of the ACM

Sigcomm96, 1996

Allan K. Y. Wong, May T. W. Ip, Richard S. L. Wu, A

Novel Dynamic Cache Size Adjustment Approach for

Better Data Retrieval Performance over the Internet,

Journal of Computer Communications, 26(14), 2003.

ICE-B 2007 - International Conference on e-Business