AN ADAPTIVE SHILL BIDDING AGENT

Jarrod Trevathan, Alan McCabe and Wayne Read

School of Maths, Physics and Information Technology

James Cook University

Keywords:

Online auction fraud, extrema avoidence, prediction, software bidding agent, artiﬁcial intelligence.

Abstract:

This paper presents a software bidding agent that inserts fake bids on the seller’s behalf to inﬂate an auction’s

price. This behaviour is referred to as shill bidding. Shill bidding is strictly prohibited by online auctioneers,

as it defrauds unsuspecting buyers by forcing them to pay more for the item. The malicious bidding agent

was constructed to aid in developing shill detection techniques. We have previously documented a simple

shill bidding agent that incrementally increases the auction price until it reaches the desired proﬁt target, or it

becomes too risky to continue bidding. This paper presents an adaptive shill bidding agent which when used

over a series of auctions with substitutable items, can revise its strategy based on bidding behaviour in past

auctions. The adaptive agent applies a novel prediction technique referred to as the Extremum Consistency

(EC) algorithm, to determine the optimal price to aspire for. The EC algorithm has successfully been used

in handwritten signature veriﬁcation for determining the maximum and minimum values in an input stream.

The agent’s ability to inﬂate the price has been tested in a simulated marketplace and experimental results are

presented.

1 INTRODUCTION

Agent based negotiation is now an integral part of on-

line auctions and online share trading. An ever in-

creasing number of transactions are being performed

by automated bidding agents. However, limited at-

tention has been paid to the security implications of

using bidding agents, or the damage such agents can

inﬂict when operating in an undesirable or fraudulent

manner. Similar to a virus or worm, a malicious bid-

ding agent can behave with an intent to do an auc-

tion harm. This might be in the form of inﬂating the

auction’s price with fake bids (i.e., shilling), attacking

the cryptographic protocols of a “secure” auction sys-

tem, or launching a denial of service attack against the

Auctioneer. In an extreme example, terrorists might

unleash a malicious agent to trade in, and hinder the

world’s stock exchanges, in an attempt to undermine

the ﬁnancial system. Alternately, they may attempt

to obtain funds through fraudulent activities in auc-

tions. Therefore the threat posed by malicious bid-

ding agents to electronic commerce is very serious.

The Research Auction Server (RAS)

at James

Cook University, is an online server for conducting

research into security issues regarding online auctions

http://auction.math.jcu.edu.au

(see (Trevathan and Read, 2006)). We are developing

methods to detect shill bidding behaviour. Both real

and simulated auctions are performed to test the effec-

tiveness of the detection methods. To aid in testing,

we developed a software bidding agent which bids in

a manner consistent with a shill. All bidding agents

created thus far operate in a controlled and near per-

fect environment. In contrast, human agents can be

devious, which is reﬂected in real-world markets. As

it is not permitted to use malicious agents on com-

mercial online auctions, or in academic agent compe-

titions (see (Wellman and Wurman, 2003)), we have

created an agent interface for RAS. RAS allows the

agents to be tested in a controlled (and legal) manner.

Note that we do not condone the use of these agents in

any manner outside the scope of this research. By de-

veloping malicious bidding agents as in this paper, we

hope to better understand the characteristics of such

agents, and how to protect against the damage they

inﬂict.

We have previously documented a software bid-

ding agent that follows a simple shill bidding strategy

(see (Trevathan and Read, 2007)). The agent incre-

mentally increases the price during an auction, forc-

ing legitimate bidders to submit higher bids in order

to win an item. The agent ceases bidding when the

Trevathan J., McCabe A. and Read W. (2007).

AN ADAPTIVE SHILL BIDDING AGENT.

In Proceedings of the Second International Conference on e-Business, pages 5-14

DOI: 10.5220/0002110600050014

 SciTePress

desired proﬁt from shilling has been attained, or in

the case that it is too risky to continue bidding with-

out winning the auction (e.g., during slow bidding or

near the auction’s end). Experimental results showed

that the agent was able to inﬂate an auction’s average

price by up to 25%, depending the level of risk the

agent was prepared to have.

This paper presents an adaptive shill bidding

agent. When used over a series of auctions with sub-

stitutable items, the adaptive agent is able to revise

its strategy based on bidding behaviour in past auc-

tions. The adaptive agent applies a novel prediction

technique referred to as the Extremum Consistency

(EC) algorithm, to determine the optimal price to as-

pire to. The EC algorithm has successfully been used

in handwritten signature veriﬁcation for determining

an input stream’s maximum and minimum values in

real-time (see (McCabe and Trevathan, 2006)). The

agent’s ability to inﬂate the price has been tested in

a simulated marketplace and experimental results are

presented. We show that the EC algorithm is supe-

rior to other valley and peak detection algorithms in

an auctioning application.

This paper is organised as follows: Section 2

presents a simple shill bidding agent that shills in a

single auction. Section 3 presents an adaptive shill

bidding agent that uses the past history of auctions to

predict and revise its strategy. Section 4 evaluates the

adaptive agent’s performance in terms of its ability to

manipulate the auction in a manner that beneﬁts the

seller. Section 5 provides some concluding remarks.

2 A SIMPLE SHILL BIDDING

AGENT

This section presents a simple shill bidding agent that

uses bogus bids to inﬂate an auction’s price. This sec-

tion provides an insight into general shill behaviour.

We brieﬂy describe the agent’s goals, how it interacts

in the auction, and its strategic directives governing

shilling (see (Trevathan and Read, 2007) for a full de-

scription).

The main goal for shilling is to artiﬁcially inﬂate

the price for the seller beyond what legitimate bidders

would otherwise require to win the item. The seller’s

pay-off is the difference between the ﬁnal price and

the uninﬂated price. A shill’s goal is to lose each auc-

tion. A shill is not constrained by a budget, but rather

a proﬁt margin. If the shill wins, the item is resold

in a subsequent auction. However, there is a limit on

how many times this can be done. For each auction

a shill wins, the seller incurs auction listing fees and

is required to invest more time. Continual wins erode

the proﬁt from shilling on the item.

The shill faces a dilemma for each bid they sub-

mit. Increasing a bid could marginally increase the

seller’s revenue. However, raising the price might

also result in failure if it is not outbid before the auc-

tion terminates. The shill must decide whether to

‘take the deal’, or attempt to increase the pay-off.

On the contrary, a bidder’s goal is to win. A bidder

has a ﬁnite budget and is after the lowest price possi-

ble. Increasing a bid for a legitimate bidder decreases

the money saved, but increases the likelihood of win-

ning. The following outlines typical shill behaviour

and characteristics:

• A shill tends to bid exclusively in auctions only

held by one (or a few) particular seller(s).

• A shill generally has a high bid frequency. An

aggressive shill will continually outbid legitimate

bids to inﬂate the ﬁnal price. A shill typically will

bid until the seller’s expected pay-off for shilling

has been reached. Or until the shill risks winning

the auction (e.g., near the termination time or dur-

ing slow bidding).

• A shill has few or no winnings for the auctions

participated in.

• It is advantageous for a shill to bid within a small

time period after a legitimate bid. Generally a

shill wants to give legitimate bidders as much time

as possible to submit a new bid before the closing

time of the auction.

• A shill usually bids the minimum amount required

to outbid a legitimate bidder. If the shill bids an

amount that is much higher than the current high-

est bid, it is unlikely that a legitimate bidder will

submit any more bids and the shill will win the

auction.

• A shill’s goal is to try and stimulate bidding. As a

result, a shill will tend to bid more near the begin-

ning of an auction. This means a shill can inﬂu-

ence the entire auction process compared to a sub-

set of it. Furthermore, bidding towards the end of

an auction is risky as the shill could accidentally

win.

2.1 The Auction Process and the

Agent’s Interaction

This paper restricts its attention to online English auc-

tions resembling those commonly used online. How-

ever, many of the principles can be extended to Con-

tinuous Double Auctions which are used in online

share trading applications.

ICE-B 2007 - International Conference on e-Business

In order to participate in an auction, a bidder must

, which they use to submit bids. During the ini-

tialisation stage, the Auctioneer sets up the auction

and advertises it (i.e., item description, starting time,

etc). An auction is given a unique number, a

, for

identiﬁcation purposes. In the bidding stage, a bidder

computes his/her bid and submits it to the Auctioneer.

The agent can place a bid in auction a

, for price p

′

by invoking the submit bid(a

, p

′

) function.

The Auctioneer must supply intermediate infor-

mation to the agent pertinent to the auction’s current

state. The agent can request a price quote for a par-

ticular auction by invoking the obtain price quote(a

)

function. This includes the start, end and current

time for the auction, and the starting bid (if one ex-

ists). It is assumed that the agent has access to the

entire bid history up to the current time in the auc-

tion. The history can be considered as an ordered

set

H = {h

,...,h

}, |H | = n, that contains price

quote triples h

= (time, price,b

), where 1 ≤ i ≤ n.

The last element is the latest price quote for the auc-

tion (i.e., h

is the current highest bid).

Finally, during the winner determination stage,

the Auctioneer chooses the winner according to the

auction rules (e.g., who has the highest bid, whether

the reserve has been met, etc.).

2.2 Operation of the Simple Shill

Bidding Agent

The agent’s goal is to maximise the proﬁt from

shilling, while avoiding winning the auction. A shill

that wins the auction is deemed to have failed. The

shill agent bids according a strategy deﬁned by a set

of directives depending on the current auction state.

Each directive plugs into the agent interface which

dictates its bidding behaviour. The directives are as

follows:

- Only bid the minimum amount required. As

part of the price quote, the Auctioneer also provides

the minimum amount required to out bid the highest

bid. This is usually calculated as a percentage of

the current high bid, or determined according to

a scalable amount depending on the value of the

current high bid. D

(p) is a function that takes the

current price, p, and returns the minimum amount the

shill should bid.

- Bid quickly after a rival bid. The agent

must bid immediately in order to inﬂuence the other

bidders for the maximum time.

- Don’t bid too close to the end of an auction.

If the shill bids too close to the end of an auction,

it risks winning. To avoid this, the agent has a risk

limit, θ. The agent is prohibited from bidding if the

auction is more than θ% complete. This is referred

to as the shill time limit. Larger values of θ increase

the risk that a shill might win an auction. D

(θ) is a

function that takes the risk limit θ, and returns true or

false regarding whether the agent should continue to

bid.

- Bid until the target price has been reached.

(α) is a function that takes the current price p,

the shill’s target price α, and returns true or false

regarding whether the agent should continue to bid.

The agent will only bid when the current price p, is

less than or equal to α.

- Only bid when the current bidding volume is

high. The agent should preferably bid more towards

the beginning of an auction and slow down towards

the shill time limit, unless the bidding activity is

high. That is, the volume of bidding must increase

throughout the auction for the shill to maintain the

same frequency of bidding. The agent uses the bid

history

H , to analyse the current bid volume and

decide whether to submit a bid. The agent observes

the previous number of bids for a time interval. If the

number of bids for the period is below a threshold,

then the agent does not submit a bid. When no bids

have been submitted for an auction, the shill agent

will attempt to stimulate bidding by submitting the

ﬁrst bid. This is a common practice in auctions. It

is intended that psychologically the presence of an

initial bid raises the item’s worth, as competitors see

that it is in demand. D

(µ) is a function that takes

the risk limit µ, and returns true or false regarding

whether the agent should continue to bid.

The following pseudocode illustrates the agent’s

behaviour:

shill agent(

aid

)

{

obtain price quote(

aid

)

if (

(θ)

AND

(p,α)

AND

(µ)

)

submit bid(

aid

(p)

)

}

while (

(θ)

AND

(p,α)

)

}

The agent initially requests a price quote. If no

bids have been submitted, then D

returns true and

the agent submits a bid for the amount returned by

. The agent then repeatedly requests price quotes

to ensure that it is able to bid quickly if there is a

rival bid (i.e., D

). When a rival bid is submitted,

the agent will bid only if the remaining directives D

and D

are satisﬁed. The agent executes in this

AN ADAPTIVE SHILL BIDDING AGENT

manner (i.e., requesting and evaluating price quotes),

until either D

or D

becomes false.

3 AN ADAPTIVE SHILL BIDDING

AGENT

In the case where there are multiple auctions for sub-

stitutable items (i.e., all items are the same), a shill

agent can learn information that may help it be more

successful over time. For example, if the ﬁnal price

for a series of auctions is constantly above the shill

target price, then the agent can revise its target price

upward. Alternately if the shill fails by not meeting

its target, then it can revise the target price down. We

refer to this as an adaptive shill bidding agent.

The adaptive agent is based on the simple shill

agent and follows the same strategy. However, the

adaptive agent supplies the simple agent with differ-

ing risk values based on previous experience. This

allows the simple shill agent to alter its strategy for

each auction. This section describes the adaptive shill

bidding agent’s lifecycle, as well as the underlying

prediction and revision techniques.

3.1 Approach

The adaptive shill agent operates in four phases:

preparation, planning, execution and revision. Each

of these stages are described in turn.

In the preparation phase, the agent is given a set

of target auctions in which it will participate. The

user provides the agent with the reserve price r, and a

risk factor φ, 0 ≤ φ ≤1, which will dictate how much

proﬁt the shill can aspire to obtain. The agent is also

supplied with bidding histories from similar past auc-

tions. The prediction method uses the bidding his-

tories to build a function, that given a bidding price,

returns the probability that the price will win.

In the planning phase, the bidding agent sets the

target price α, equal to the corresponding price with a

probability indicated by the risk factor φ, according to

the historical winning bid distribution. If α < r, then

the agent requests the user to lower r and/or increase

φ. It is assumed that all auctions are held by one seller

at the same auction house. If two auctions overlap

(i.e., execute simultaneously), concurrently executing

agents do not affect each other’s operation.

In the execution phase, the adaptive agent executes

the bidding plan by successively placing bids in each

of the selected auctions (via the simple agent). The

adaptive agent executes in a particular auction until

the simple agent terminates (i.e., it reaches α or the

time limit).

In the revision phase, the predictive bid function

is updated with the auction’s results depending on the

agent’s performance. Let φ

′

be the revised agent’s risk

factor, where r ≤ φ

′

≤ φ. φ

′

is raised or lowered de-

pending on the shill’s success. The agent selects the

next auction from the set of target auctions and re-

enters the execution phase with α corresponding to

′

3.2 Prediction Methods

The adaptive agent constructs a probability function

from the bidding histories of past auctions. In an En-

glish auction, the ﬁnal price reﬂects the valuation of

the second highest bidder. That is, the winner does

not disclose the true highest amount they were will-

ing to pay. Contrast this with First Price Sealed Bid

(FPSB) and Vickrey auctions. In these auctions, bids

are sealed so that a bidder does not know the value

of anyone else’s bid. The winner is the bidder with

the highest bid. A FPSB auction requires the winner

to pay an amount equal to the highest bid, whereas in

a Vickrey auction, the winner pays an amount equal

to the second highest bid. Constructing a probability

function from a FPSB auction would yield an accu-

rate depiction of the bidders’ true valuation of an item.

However, the Vickrey auction’s probability function is

the same as an English auction, in that only the win-

ner’s second highest valuation is possibly known.

Extrapolation techniques have been proposed to

approximate the winner’s true valuation from a set

of past English auctions (see (Dumas et al, 2002)).

However, this information is not required by the shill

agent. The shill’s goal is to force the bidder into bid-

ding their true valuation. Knowledge of the second

highest price is satisfactory, as the shill can assume

that by bidding somewhere within the range of the

second highest price, that the buyer will be forced into

inﬂating their bid nearer to his/her true valuation. It is

too risky for the shill to try bid up to, or at the bidder’s

true valuation. Bidding at the second highest price is

a much safer strategy, and should capture the majority

of the desired proﬁt from shilling.

(Dumas et al, 2002) propose two methods that a

bidding agent can use to construct a probability func-

tion. The ﬁrst uses a histogram of the ﬁnal auction

prices, to be the function that maps a real number x,

to the number of past auctions whose ﬁnal price was

exactly x. The ﬁnal price of an auction a with no bids

and zero reserve price, is then modeled as a random

variable f p

, whose probability distribution, written

P( f p

= x), is equal to the histogram of ﬁnal prices,

scaled down so that its total mass is 1. The probability

of winning an auction with a bid of z assuming no re-

ICE-B 2007 - International Conference on e-Business

serve price, is given by the cumulative version of this

distribution, that is P( f p

≤z) =

∑

0≤x≤z

P( f p

= x),

for an appropriate discretisation of the interval [0,z].

For example, if the sequence of observed ﬁnal prices

is [20, 18, 23], the cumulative distribution at the be-

ginning of an auction is:

(z) = P( f p

≤ z) =











1 for z ≥ 23

0.66 for 20 ≤ z < 23

0.33 for 18 ≤ z < 20

0 for z < 18

In the case of an auction a with quote q > 0 (which

is determined by the reserve price and the public bids)

the probability of winning with a bid of z is:

(z) = P( f p

≤ z| f p

≥ q)

P( f p

≤z ∧ f p

≥q)

P( f p

≥z)

∑

q≤x≤z

P( f p

=x)

∑

x≥q

P( f p

=x)

In particular, p

(x) = 0 if z < q.

(Dumas et al, 2002) identify two drawbacks with

the histogram method. First, the computation of the

value of the cumulative distribution at a given point,

depends on the size of the set of past auctions. Given

that the shill agent heavily uses this function, this can

create an overhead for large sets of past auctions. Sec-

ond, the histogram method is inapplicable if the cur-

rent quote of an auction is greater than the ﬁnal price

of all the past auctions, since the denominator of the

above formula is then equal to zero. Intuitively, the

histogram method is unable to extrapolate the proba-

bility of winning in an auction if the current quote has

never been observed in the past.

The normal method addresses these two draw-

backs, although it is not applicable in all cases. As-

suming that the number of past auctions is large

enough (more than 50), if the ﬁnal prices of these auc-

tions follow a normal distribution with mean µ and

standard deviation σ, then the random variable f p

can be given a normal distribution N(µ,σ). The prob-

ability of winning with a bid z in an auction a with no

bids and zero reserve price, is then given by the value

at z of the corresponding cumulative normal distribu-

tion:

(z) = P( f p

≤ z) =

√

2πσ

z−µ

−∞

−x

If the current quote q of an auction a is greater than

zero, the probability of winning this auction with a

bid of z is:

(z) = P( f p

≤ z| f p

≥ q)

P( f p

≤z ∧ f p

≥q)

P( f p

≥q)

z−µ

q−µ

−x

∞

q−µ

−x

The complexity of these algorithms is only depen-

dent on the required precision, not on the size of the

dataset from which µ and σ are derived. Hence the

normal method can scale up to large sets of past auc-

tions. The normal method is able to compute a prob-

ability of winning an auction with a given bid, even if

the value of the current quote in that auction is greater

than all the ﬁnal prices of past auctions. The do-

main of the normal distribution is the whole set of real

numbers, unlike discrete distributions such as those

derived from histograms. (Dumas et al, 2002) per-

formed an analysis of datasets from eBay and Yahoo

and showed that the ﬁnal prices of a set of auctions

for a given item are likely to follow a normal distribu-

tion. This is due to a given item having a more or less

well-known value, around which most of the auctions

should ﬁnish.

Figure 1 A illustrates how the adaptive agent per-

forms on an example auction dataset using the afore-

mentioned approach. The auction data is ordered ac-

cording to time. A histogram is given showing the bid

frequency. From this a cumulative probability distri-

bution is derived. The adaptive agent is initially sup-

plied with the risk parameter φ, 0 ≤ φ ≤ 1. The price

corresponding to φ in the cumulative distribution is

the maximum price the agent is willing to bid. α can

be set to any price in the probability range up to φ. In

this example, the agent’s risk factor φ is 0.75, there-

fore the agent can set α up to $6.85.

If the history of past auctions covers a large pe-

riod of time, data aging must be taken into account.

The normal method can be adapted to consider time-

weighted averages and standard deviations of prices.

In this way, recent observations are given more impor-

tance than older ones. Figure 1 B illustrates a time-

weighted curve. In this example, the average time

for a price observation is multiplied by its cumulative

distribution and cumulatively summed. This value

is then normalised against the maximum and mini-

mum observations to give the time weighted cumula-

tive distribution. The agent’s risk factor φ remains the

same 0.75, but α increases to $8.48.

However, a time-weighted approach alone may

not give the best results. Permanent price increases do

occur over time due to inﬂation and other economic

factors. As a result, past bids are no longer valid.

Furthermore, temporary extreme price skews can

also affect the process thus resulting in erroneous

predictions. To address these problems, we propose

that a valley/peak detection algorithm be used in

determining the optimum target price.

www.yahoo.com/auction

AN ADAPTIVE SHILL BIDDING AGENT

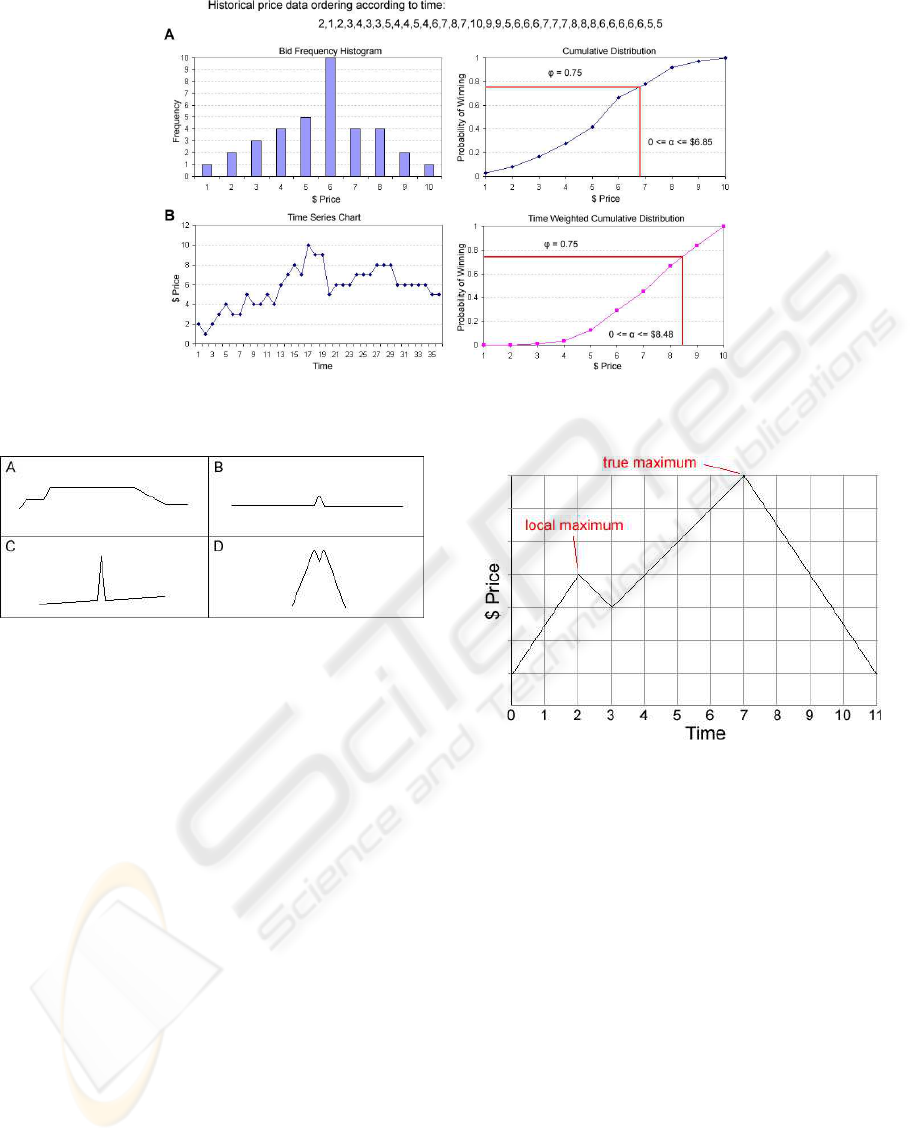
Figure 1: Example illustrating how the adaptive agent basically plans and revises its strategy.

Figure 2: Example maximum situations encountered in an

auction dataset.

Finding the true maximum/minimum price in

real-time

The adaptive agent uses a novel approach for de-

termining the correct price to set α in the presence

of data aging and extreme price skews. This is re-

ferred to as the Extremum Consistency (EC) algo-

rithm (see (McCabe and Trevathan, 2006)). The EC

Algorithm is used to ﬁnd the true maxima or minima

in a noisy input stream. The algorithm was initially

developed for use in Handwritten Signature Veriﬁ-

cation. The problem arose when trying to detect a

signature’s turning points, and changes in other dy-

namic characteristics such as velocity and pressure in

real-time. Noise is common in this environment due

to hardware inaccuracies, which makes choosing the

correct extrema difﬁcult. The EC algorithm is able to

avoid false extrema based on a tolerance parameter.

The adaptive agent uses the EC algorithm to deter-

mine the true maximum and minimum winning prices

over a series of auctions. This allows the agent to

set α according to the risk between these two ex-

tremes. As auction closing prices tend to oscillate

around about a trend line, the agent needs the abil-

Figure 3: Example showing a local maximum and a true

maximum.

ity to distinguish meaningless price ﬂuctuations from

true extrema. The agent can update α between auc-

tions when a new maximum or minimum is encoun-

tered (in real-time). For example, when the price in-

creases over time due to inﬂation.

Figure 2 presents several examples of maximum

situations encountered in auction datasets. Figure 2 A

clearly has a single valid maximum. However B and

C are most likely due to noise and should be ignored.

D contains only a single valid maximum, where the

dip between the two peaks is probably also due to

noise (i.e., insigniﬁcant price ﬂuctuations). The EC

algorithm’s goals in the auction application are:

1. Ignore meaningless price skews (noise).

2. Find the true maximum and minimum price in

real-time.

The EC algorithm takes a different approach to other

ICE-B 2007 - International Conference on e-Business

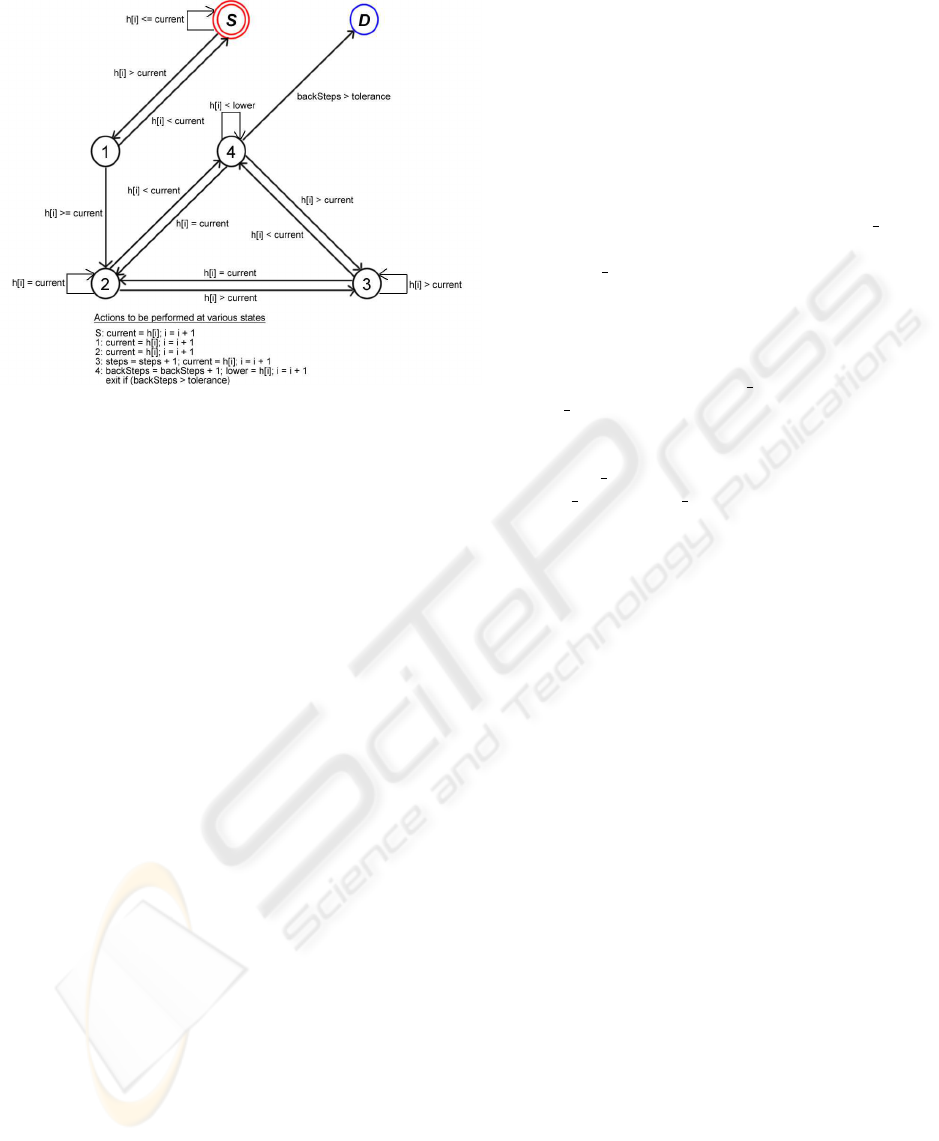
Figure 4: A ﬁnite state machine expressing the

EC.

algo-

rithm for ﬁnding the “width” of, or number of “steps” in,

the initial upslope of a peak. The movements between ver-

tices (states) are deﬁned by the comparison between points

in the input stream and the comparisons are included on

the edges in the diagram. Additionally there are actions to

be performed when some vertices are reached - these are

also included in the diagram. Note that in this table, h[i]

refers to the i

element in the list of stream values h. Once

the

backSteps

parameter exceeds the

tolerance

, the al-

gorithm enters the dead state D and we have the width of

the slope in the

steps

parameter. The width of the downs-

lope is similarly calculable, with the inversion of various

state transition conditions and the width of the valley itself

is then the minimum of the downslope width and upslope

width. Likewise, the width of peaks can be found with min-

imal modiﬁcations to the algorithm.

techniques such as hill climbing or convolution, in

that it examines the width (or consistency) of an ex-

tremum rather than just its depth or height. This al-

lows it to compensate for noise. In an auctioning ap-

plication, noise to due to abnormal observations in the

dataset such as an extreme price skew. Extreme price

skews can occur for various economic factors. For ex-

ample, supply of an item dramatically drops, whereas

demand remains the same. This can occur when crops

are destroyed by a storm, or war breaks out in the

Middle East which restricts oil supply. Furthermore,

an extreme price skew may occur when conﬁdence in

a particular item is momentarily low, such as an ex-

tortion threat to poison chocolate bars.

Figure 3 illustrates a dataset which contains two

maximums, only one of which is valid. A local incor-

rect maximum is at Time = 2. In this case the peak

itself is actually very short and using the maximum

or mean slope size would make the peak appear er-

roneously large – the use of the minimum slope size

is much more accurate. By placing a threshold on

the width, this peak will ideally be ignored and that

at Time = 7 would be taken as the more appropriate

maximum. Figure 4 illustrates how the EC algorithm

operates.

In shill application, the EC algorithm is used to

determine which values should be included in the

probability distribution. Initially, the known maxi-

mum and minimum are set equal to the ﬁrst item in

the dataset. Two instances of the EC algorithm are

run concurrently. The ﬁrst is referred to as EC

Max,

and is tasked with searching for the latest maximum.

Likewise EC Min searches for the latest minimum.

Once one of these algorithms terminates, this value

is used as the current extremum and then the cor-

responding EC algorithm is executed. This process

continues until the end of the dataset. For example,

at the start of a dataset, if EC

Min terminates ﬁrst,

then EC

Max is prematurely terminated, its results

discarded, and then run from the newly found mini-

mum until a new max is found. Once the new max

is found, EC

Min is executed starting from the new

max. EC

Max and EC Min alternate in this manner

throughout the dataset.

Figure 5 illustrates the process of how the agent

uses extrema to aid its predictions. In this exam-

ple, the EC algorithm with a tolerance parameter of

3, reveals that there are three minima ($1, $5, $5)

and three maxima ($8, $10, $8). The probability dis-

tribution only includes the values between a maxi-

mum/minimum pair. As the extremum are updated

in real-time, this yields four different distributions for

this example. We refer each maximum/minimum pair

as an epoch. Once a new extremum has been deter-

mined, the agent uses the most recent epoch and ig-

nores all other past values. Each new value encoun-

tered in the yet undetermined epoch is also incorpo-

rated into the current epoch’s probability distribution.

On discovery of the next extremum, the epoch cur-

rently in use is discarded and the newly discovered

epoch used.

The tolerance parameter is altered according to the

outlook. A small tolerance is used for short term pre-

dictions and high tolerance for long term predictions.

In the ongoing example, increasing the tolerance re-

sults in the minimum and maximum being determined

as $1 and $10 respectively.

3.3 Revision Strategies

In the revision phase, the agent assesses its perfor-

mance and revises its strategy. If the agent is success-

ful in that it did not win the auction and achieved its

target, the value of the winning bid h

, is incorporated

into the current epoch. φ

′

is revised upwards by a fac-

AN ADAPTIVE SHILL BIDDING AGENT

Figure 5: Example illustrating how the EC algorithm inﬂuences the agent’s probability function. Epochs are created between

max/min pairs in the time series chart (top). Prices further in past are discarded. The agent uses the price corresponding to φ

for the current epoch in use.

tor ε, where φ

′

+ ε ≤ φ.

If the agent has failed by winning the auction,

then φ

′

is revised downward by a factor ε, where

r ≤ φ

′

−ε. When the shill fails in this manner, the

second highest bid (i.e., h

n−1

), is added to the current

epoch and the shill’s winning price is discarded. If

the agent did not win, and failed to achieve its target,

′

remains the same. The value of the winning bid h

is still incorporated into the current epoch.

Determining the agent’s risk proﬁle

A riskier shill can achieve more proﬁt, but at the

increased likelihood of winning an auction. Direc-

tives D

and D

determine whether the agent should

bid based on the current auction time and bid volume.

The agent can also revise other risk factors in re-

sponse to historical bidding patterns. θ can be in-

creased if bidding in previous auctions has tended to

occur closer to the end of an auction. Likewise, µ can

be increased if the bid frequency in previous auctions

is low.

4 PERFORMANCE

This section describes the performance of the adaptive

shill bidding agent. Claims regarding the simple shill

agent can be found in (Trevathan and Read, 2007).

The adaptive agent is implemented on RAS and has

been tested with other types of bidding agents in a

simulated auction market. The adaptive shill agent

is assessed on its ability to inﬂate an auction’s ﬁnal

price. A shill bidding agent is considered successful

if the ﬁnal price equals or exceeds the shill’s target

price. The shill agent is considered unsuccessful if it

won the auction, or failed to reach the target price.

4.1 Elements of the Experimental Setup

Seed data a dataset was obtained from a series of

simulated auctions. This was used as a “seed” to

initialise the shill agent (i.e., provide it with an initial

epoch).

Zero Intelligence (ZI) Bidder This bidding agent

is designed to simulate an ordinary bidder in an

auction. It is assigned a random amount which it tries

to submit as a proxy bid at a random time throughout

the auction. A ZI bidder’s limit price is generated

randomly based on the a trend factor. Speciﬁcally,

a predetermined trend was programmed which

randomly assigns the agent’s limit price between

a given maximum and minimum. The extremum

were increased and decreased over time to give the

appearance of natural price trends (compared to

ICE-B 2007 - International Conference on e-Business

completely random prices).

Shill Bidder This is an implementation of the

adaptive shill bidding agent proposed in this paper.

The shill agent has a reserve price r, and a proﬁt risk

factor φ. The agent’s target price α, is determined

according to the current epoch, and its strategy is

adjusted using the aforementioned revision technique.

Auction A software simulated auction. The auction

has a start and end time. The bidding agents can sub-

mit bids during this time, where the auction outcome

depends on the auctions of the agents. All auctions

are English auctions with proxy bidding.

4.2 Claims, Experiments, and Results

Claim 1 The adaptive shill agent achieved a higher

success rate than the simple shill agent. To validate

this claim, we pitted the adaptive agent against

the simple agent using the same dataset and risk

parameters. On average (for the speciﬁc dataset),

the adaptive agent achieved an 82% success rate,

whereas the simple agent achieved a 43% success

rate. The amount of proﬁt acquired by the adaptive

agent was 36% greater than the simple agent. This

seems to indicate that it is worthwhile employing the

adaptive agent.

Claim 2 A riskier agent achieved a higher average

ﬁnal price than an agent following a safer strategy.

The agent was run on the same dataset with increas-

ing values of φ. The riskier agent was able to achieve

a 15% increase in the average ﬁnal price compared

to a risk-adverse agent. However, this came at the

expense of an increased failure rate due to winning.

Claim 3 EC produced better results than simple gra-

dient descent, thresholding and convolution. To im-

prove the agent’s proﬁt, two alternate algorithms were

implemented: simple removal of small valleys or

peaks (called “thresholding”) and basic convolution

of the data prior to gradient-descent/hill-climbing.

Thresholding involved determining the distance be-

tween the peak’s location and the preceding valley’s

location (that is, the depth of a valley or height of a

peak). If this distance was below a speciﬁed threshold

then that peak was ignored and the traversal continued

in the same direction.

Examples of situations where thresholding was

successful can be seen in Figure 2 B and C. However,

the agent’s overall performance (in terms of proﬁt

acquired) was quite poor. The reason it seems, is

that a peak’s height alone, while obviously containing

Table 1: Proﬁt acquired by shilling.

Technique Avg Final Price

Simple Hill Climbing $ 4.80

Thresholding $ 5.11

Convolution and Hill Climbing $ 6.20

$ 6.90

useful information, is not the best validity indicator

(at least in this environment), but rather the consis-

tency/duration is more important.

Convolution is a method for “smoothing out” or

“averaging” one-off “bumps” or random noise while

attempting to preserve those extrema which are truly

indicative of the price trend direction. The basic

idea behind convolution is that a window of some

ﬁnite length is scanned across the stream of val-

ues (Hirschman et al, 2005). The output price is the

weighted sum of the input prices within the window

where the weights can be adjusted to perform vari-

ous ﬁltering tasks - when smoothing is performed the

weights are generally all equal. After the input stream

was convoluted the hill-climbing/gradient-descent ap-

proach was used to obtain the extrema.

Table 1 summarises the error rates of the imple-

mented approaches used by the adaptive shill agent.

The

algorithm clearly achieves more signiﬁcant re-

sults.

The

algorithm’s main advantage over convo-

lution is execution speed. In a real-time application

such a continuous double auction, execution speed

can become a serious issue. In order to perform con-

volution an entire extra layer of computation is re-

quired, as convolution of the raw data must be done

prior to obtaining the extrema, whereas with the

algorithm the checking is done at the same time as

the search for extrema. Additionally, convolution can

become quite expensive using a large window or with

a large raw data size.

Empirical experimentation with the adaptive shill

bidding agent has found that convolution causes an

average slowdown of 20-25% (depending on system

parameters). The number of extra calculations

required in the

algorithm compared to naive

hill-climbing is almost negligible with the slowdown

of the shill agent experimentally found to be less than

3%.

Claim 4 The adaptive agent’s prediction method can

be reasonably applied to share market prediction.

The prediction method was run on a data obtained

from the Australian Stock Exchange. As previously

mentioned, shares are traded in an auction type re-

ferred to as a Continuous Double Auction. A Con-

AN ADAPTIVE SHILL BIDDING AGENT

tinuous Double Auction has many buyers and sell-

ers continually trading a commodity. Rather than

shilling, the prediction method was used to deter-

mine maximum and minimum cycles in the closing

prices for several listed companies. While the predic-

tion method can not exactly determine when a new

extremum will be encountered, it deﬁnitely can tell

when an extremum has occurred and which direction

the current price is moving. In this case, we pro-

grammed the agent to purchase shares immediately

after a minimum had been determined, and sell these

once the corresponding maximum had been found.

We also reversed this process. Depending on the its

risk, for most datasets the agent was able to make a

proﬁt (i.e., ﬁnish with a greater value than initially

provided). It is interesting to note that the latter ap-

proach (i.e., purchasing shares after the maximum

and selling upon determining the minimum) produced

better results.

5 CONCLUSIONS

This paper presents an adaptive shill bidding agent.

When used over a series of auctions with substitutable

items, the adaptive agent is able to revise its strat-

egy based on bidding behaviour in past auctions. The

adaptive agent applies a novel prediction technique

referred to as the Extremum Consistency (EC) algo-

rithm, to determine the optimal price to aspire for.

The EC algorithm has successfully been used in hand-

written signature veriﬁcation for determining an input

stream’s maximum and minimum values in real-time.

The agent’s ability to inﬂate the price has been tested

in a simulated marketplace and experimental results

are presented. We show the superiority of the EC

algorithm over other valley and peak detection algo-

rithms.

In future work it would be useful to investigate

agents that attack security protocols or launch denial

of service attacks against the Auctioneer. Further-

more, we plan to devise a shill bidding agent that

proﬁles other bidders based on their bidder id. The

agent alters its strategy in response to the bidder’s an-

ticipated strategy based on previous observations. Fi-

nally, similar problems to shilling occur in Continu-

ous Double Auctions such as “ramping the market”.

It would be intuitive to investigate agents that conduct

this kind of fraud.

REFERENCES

Hirschman, I. and Widder, D. (2005). The Convolution

Transform. Dover Publications.

Cliff, D. (1997). Minimal-intelligence agents for bargaining

behaviours in market-based environments, Hewlett

Packard Labs, Technical Report HPL-97-91.

Dumas, M., Aldred, L. and Governatori, G. (2002). A prob-

abilistic approach to automated bidding in alterna-

tive auctions, In Proceedings of the 11

International

Conference on World Wide Web, 99–108. ACM Press.

Gjerstad, S. and Dickhaut, J.(1998). Price formation in dou-

ble auctions, Games and Economic Behavior, 22, 1–

29.

Gode, D. and Sunder, S. (1993). Allocative efﬁciency of

markets with zero intelligence traders: Market as a

partial substitute for individual rationality, Journal of

Political Economy, 101, 119–137.

McCabe, A. and Trevathan, J. (2006). A new approach to

avoiding the local extrema trap, In Proceedings of the

International Computational Techniques and Ap-

plications Conference.

Rust, J., Miller, J. and Palmer, R. (1992). Behaviour of trad-

ing automata in a computerized double auction mar-

ket, In The Double Auction Market: Institutions, The-

ories, and Evidence. Addison-Wesley.

Schwartz, J. and Dobrzynski, J. (2002). 3 men are charged

with fraud in 1 100 art auctions on eBay, The New

York Times.

Trevathan, J. and Read, W. (2006). RAS: a system for sup-

porting research in online auctions, ACM Crossroads,

12.4, 23–30.

Trevathan, J. and Read, W. (2007). A simple shill bidding

agent, In Proceedings of the 4

International Confer-

ence on Information Technology - New Generations,

933–937.

Wellman, M. and Wurman, P. (2003). The 2001 trading

agent competition, Electronic Markets, 13.1, 4–12.

ICE-B 2007 - International Conference on e-Business