APPROXIMATE ANALYSIS OF A CALL CENTER WITH
SKILL-BASED ROUTING
Chul Geun Park
Department of Information and Communications Engineering, Sunmoon University, Kalsan 100, Asan-si, Korea
Dong Hwan Han
Department of Mathematics, Sunmoon University, Kalsan 100, Asan-si, Korea
Keywords:
Call center, N-design, Skill-based, Queueing analysis, Performance.
Abstract:
Call centers have become the prevalent contact points between many companies and their customers. By
virtue of recent advances in information and communication technology, the number and size of call centers
has grown dramatically. As a large portion of the operating costs are related to the labor costs, efficient design
and workforce staffing are crucial for the economic success of call centers. In this context, the workforce
staffing level can be modeled as mathematical optimization problem using queueing theory. In this paper,
we deal with an approximate analysis of the so-called N-design call center with two types of customers, two
different finite queues and two different exponential patient times. We also represent some numerical examples
and show the impact of the system parameters on the performance measures.
1 INTRODUCTION
Contact centers are service organizations for cus-
tomers who need service via the phone, facsimile, e-
mail or other telecommunication channels. A particu-
larly important type of contact center is the call center.
By virtue of recent advances in information and com-
munication technology, the number and size of call
centers as well as the number of customers and agents
grow explosively(Mand,2005). For example, in Eu-
rope, the number of call center employees in 2000
was estimated by 600,000 in the UK and 200,000 in
Netherlands and 280,000 in Germany. Indeed, some
call center statistics assess that 70% of all customer-
business information in the U.S. occur in call centers
which employ about 3% of the U.S. workforce and
1.5 million agents(Bors,2004; Stol,2004).
In the most simple design of call centers, only one
type of customers is served by one type of agents. The
prevalent model for performance analysis of these call
centers is the M/M/N queue, frequently referred as
Erlang-C. Though Erlang-C model has non-realistic
assumption of infinite lines and customer’s infinite pa-
tient times, the performance measures are easily cal-
culated. Customer’s patient times have a considerable
effect on the performance of the system(Shim,2004;
Mand,2004). This basic queueing model can be ex-
tended to the M/M/N+M queue(Erlang-A model) and
the M/M/N+G queue with patient times(Mand,2005;
Mand,2004).
The skill set of agents describes for which kind
of service the agent is skilled and how well he pro-
vides service. The customer’s requests can be routed
to different agent groups and the agents can serve
customers of different types, which is commonly re-
ferred to as skill based routing(Stol,2004). As ex-
amples of skill-based routing, we have the so-called
N-design, X-design, W-design and M-design mod-
els(Gans,2003; Stol,2003). In the N-design model,
one of two agent groups serves both types of cus-
tomers and other agents are specialists for a particular
customer type. Approximate analysis of the N-design
model with infinite waiting queue and priority service
discipline has been done(Shum,2004).
In this paper, we use an approximate analysis
method of the so-called decomposition algorithm to
reduce computational burdens. The considered N-
design model with finite waiting queues and exponen-
tial patient times is different to the previously studied
model(Shum,2004). As we know well, the approxi-
mation provides sufficient accuracy reducing the nec-
essary completion time.
45
Geun Park C. and Hwan Han D. (2007).
APPROXIMATE ANALYSIS OF A CALL CENTER WITH SKILL-BASED ROUTING.
In Proceedings of the Second International Conference on e-Business, pages 45-50
DOI: 10.5220/0002111000450050
Copyright
c
 SciTePress

-
-
Type B
Type A
λ
2
λ
1
Blocking
Blocking
?
6
?
6
Reneging(θ
1
)
Reneging(θ
2
)
Queue A
Queue B
-
-
S
S
S
Sw
Priority








Specialists
Generalists
-
-
.
.
.
µ
2
µ
2
-
-
.
.
.
µ
1
µ
1
N
2
N
1
Figure 1: N-design model with two groups of agents.
2 SYSTEM MODEL
In this section, we describe the system configuration
and routing procedure of our N-design model. As we
show Figure 1, we have an N-design model with two
types of customers A and B and two different groups
of agents, the specialists and generalists.
Both A and B customers arrive at the respective
waiting queues A and B according to Poisson pro-
cesses with respective rates λ
1
and λ
2
. Both types
of customers are patient. The type A(B) customer re-
neges his waiting in his own queue after an exponen-
tially distributed patient time with mean θ
−1
1
(θ
−1
2
), if
the service has not begun. We assume that the reneg-
ing customers are lost and so there are no retrials.
Both groups of agents are assume to have dif-
ferent skills. The first group of N
1
agents serves
only type A customers(Specialist). The other group
of N
2
agents serves both types of A and B cus-
tomers(Generalist). Service times are exponentially
distributed with means µ
−1
1
and µ
−1
2
for specialists and
generalists, respectively regardless of the customer
type. We assume that the number K
1
of A customers
waiting or being served in the system is finite. The
number K
2
of B customers in the system is finite as
well. These limitations of two waiting rooms reflect
the cases of given numbers of telephone lines for two
types of customers respectively. In this way, when K
1
A customers are in the system, an arriving A customer
receives a busy signal and lost. In the same way, the
number of B customers in the system does not exceed
the limitation K
2
.
If possible, an arriving A customer will be served
immediately by the specialist. Otherwise, if all spe-
cialists are busy, when a generalist is available, this
generalist serves the arriving A customer. If all spe-
cialists and generalists are busy, the arriving cus-
tomers join their corresponding waiting queues. The
customer selection rule of generalists depends on the
type of the customer. The specialists serve A cus-
tomers according to FCFS(First Come First Service)
rule within its own customer type. The generalist
looks at B queue first and serves a waiting B customer,
if possible. Otherwise, the generalist looks at A queue
and serves an A customer. If there is no customer in
the two queues, the generalist becomes idle. Thus the
generalist has N-design routing policy with priority
service discipline and gives non-preemptive priority
to B customers.
Now we describe an overview of the approxima-
tion procedure. The system can be represented by a
two-dimensional Markov process. Since K
1
and K
2
are finite in our N-design model, the state space of
the process is finite. So the resulting two-dimensional
Markov process has a stationary probability distribu-
tion. Let X
1
be the number of A customers in A queue
and in service with specialists in steady state. Let X
2
be the sum of the number of B customers in B queue
and the number of customers of either type in service
with generalists.
We introduce a decomposition algorithm for ap-
proximate performance analysis(Shum,2004). We
first divide the state space into four regions
S
1
= {X
1
≤ N
1
}
{X
2
< N
2
}, S
2
= {N
1
< X
1
≤
K
∗
1
}
{X
2
< N
2
}, S
3
= {X
1
≤ N
1
} {N
2
≤ X
2
≤ K
∗
2
},
and S
4
= {N
1
< X
1
≤ K
∗
1
}
{N
2
≤ X
2
≤ K
∗
2
}. Here
K
∗
1
and K
∗
2
are random variables, which will be de-
scribed in the next section. In the numerical approxi-
mation, we take the respective means K
A
= E[K
∗
1
] and
K
B
= E[K
∗
2
]. Thus, for simplicity, we think of these
variables as the numbers. Clearly, the region S
2
is
forbidden. The core of the approximation algorithm
is to find the following probabilities.
P(X
1
= i|X
2
= j) ≈ P(X
1
= i|X
2
< N
2
), (1)
P(X
1
= i|X
2
= j) ≈ P(X
1
= i|N
2
≤ X
2
≤ K
∗
2
), (2)
P(X
2
= j|X
1
= i) ≈ P(X
2
= j|X
1
≤ N
1
), (3)
P(X
2
= j|X
1
= i) ≈ P(X
2
= j| N
1
< X
1
≤ K
∗
1
). (4)
3 THE SUBMODEL ANALYSIS
Given that the system occupies in one of the regions
S
1
, S
3
and S
4
, we can easily find the system per-
formance along one-dimension by using conventional
queueing models.
3.1 To Get p
1,i
≡ P(X
1
= i|X
2
< N
2
)
Given that {X
2
< N
2
}, there is no the case {N
1
<
X
1
≤ K
∗
1
}. Under the condition {X
2
< N
2
}, A queue
ICE-B 2007 - International Conference on e-Business
46

is empty and all arriving A customers are served by
specialist until {X
1
≤ N
1
}. Thus we can model this
case as the M/M/N
1
/N
1
(Erlang-B) queue. The num-
ber of busy servers forms a Markov Birth-and-Death
process(Gross,1985).
3.2 To Get
q
2, j
≡ P(X
2
= j|N
1
< X
1
≤ K
∗
1
)
Given that {N
1
< X
1
≤ K
∗
1
}, all generalists are busy.
There is no the case {X
2
< N
2
}. In case of N
2
< j <
K
∗
2
, the state transition from X
2
= j to j − 1 occurs
with rate N
2
µ
2
. But the state transition X
2
= j to
j + 1 occurs with rate λ
2
. The waiting B customers
in B queue renege after an exponentially distributed
patient time with mean θ
−1
2
, if the service does not
begin. Thus, in this region, the submodel is well de-
scribed as the M/M/1/K
∗
2
+ M queue. Here K
∗
2
is
a random variable, which varies from the minimum
K
2
− N
2
+ 1 (all generalists serve B customers) to the
maximum K
2
+ 1 (all generalists serve A customers).
The mean B queue length can be easily calculated by
the distribution of the number of A customers served
by the generalists(Garn,2002).
3.3 To Get q
1, j
≡ P(X
2
= j|X
1
≤ N
1
)
Given that {X
1
≤ N
1
}, B customers are served by N
2
generalists with service rate µ
2
. There is no wait-
ing A customer in A queue. A customers are routed
to a generalist when all specialists are busy(X
1
=
N
1
) and there is an available generalist(X
2
< N
2
).
That is, A customers overflow to the generalist from
the M/M/N
1
/N
1
queue. We can easily model this
overflow traffic as an IPP(Interrupted Poisson Pro-
cess)(Kukz,1973).
The IPP is a Poisson process which is alterna-
tively turn on for an exponentially distributed pe-
riod(Active) and turn off for another exponentially
distributed period(Silent). During Active period, the
interarrival times of customers are exponentially dis-
tributed, while no customers are arrived during Silent
period(Onvu,1995). Let γ
−1
A
and γ
−1
S
be the mean du-
rations of the Active and Silent periods, respectively
and let λ be the customer’s arrival rate during Active
period. Let Q
I
be the infinitesimal generator of the
underlying Markov chain of the IPP and let Λ
I
be the
arrival rate matrix of the IPP. Then the IPP is com-
pletely characterized by Q
I
and Λ
I
as follows
Q
I
=

−γ
A
γ
A
γ
S
−γ
S

, Λ
I
=

λ 0
0 0

. (5)
Note that the traffic intensity offered to the
M/M/N
1
/N
1
queue is ρ
1
= λ
1
/µ
1
. Then the over-
flow traffic is easily modeled as the IPP(Kukz,1973).
Given that the overflow process is modeled as an IPP
process, we have two independent input processes to
the generalist. One of these process is the overflow
IPP process of A customers and the other is a Poisson
process of B customers with service priority against A
customers. It is well known that the superposition of
IPP and Poisson processes makes an MMPP(Markov
Modulated Poisson Process)(Heff,1986). Then the
superposed process MMPP is completely represented
by the infinitesimal generator Q and the arrival rate
matrix Λ as follows
Q = Q
I
, Λ = Λ
I
+ Λ
2
, (6)
where Q
I
and Λ
I
are given in (5) and Λ
2
=diag(λ
2
,λ
2
)
is a diagonal matrix.
Let’s return to finding the probability q
1, j
in the
condition {X
1
≤ N
1
}. Clearly, both A and B cus-
tomers are served in FCFS order until all generalists
are busy. When all generalists are busy, B customer in
B queue is served by an available generalist just com-
pleting service according to the priority rule. Then the
required probability q
1, j
is the steady state probabil-
ity that the sum of busy generalists and B customers
in B queue is j at customer’s arrival epoch to the
MMPP/M/N
2
/K
∗
2
queue. Here K
∗
2
is a random vari-
able, which varies from the minimum K
2
to the max-
imum K
2
+ N
2
. Let {(X
2
,Z)} = {( j,k)| j ≤ K
∗
2
,k =
1,2} be the Markov chain, where Z indicates the state
of the underlying Markov process of the MMPP and
X
2
indicates the number of both A and B customers in
the submodel. Let Q
∗
be the infinitesimal generator
of the chain {(X
2
,Z)}, then we have
Q
∗
=

Q
1
Q
2
O Q
3

,
where
Q
1
=










Q
1
(1) Λ ··· 0 0
µ
2
I Q
1
(2) ··· 0 0
0 2µ
2
I ··· 0 0
··· ·· ·
.
.
.
··· ···
0 0 ··· Q
1
(N
2
) Λ
0 0 ··· N
2
µ
2
I Q
1
(N
2
+ 1)
0 0 ··· 0 c
1
I










,
Q
2
=










0 0 ··· 0 0
0 0 ··· 0 0
0 0 ··· 0 0
··· ···
.
.
.
··· ···
0 0 ··· 0 0
Λ
2
0 ··· 0 0
Q
3
(1) Λ
2
··· 0 0










, Q
3
=
APPROXIMATE ANALYSIS OF A CALL CENTER WITH SKILL-BASED ROUTING
47








Q
3
(2) Λ
2
··· 0 0
c
3
I Q
3
(3) ··· 0 0
··· ·· ·
.
.
.
··· ···
0 0 ··· Q
3
(E) Λ
2
0 0 ··· c
K
∗
2
−N
2
I Q− c
K
∗
2
−N
2
I







,
where Q
1
(i) = Q − Λ − (i − 1)µ
2
I, c
k
= N
2
µ
2
+ kθ
2
,
k = 1,2,·· · , K
∗
2
−N
2
, Q
3
(i) = Q− Λ
2
−c
i
I, Q
3
(E) =
Q
3
(K
∗
2
− N
2
− 1) and Q, Λ and Λ
2
are given in (6)
and O is (K
∗
2
− N
2
− 1) × (N
2
+ 1)-dimensional zero
matrix.
To find the probability q
1, j
, let π be the station-
ary distribution of Q
∗
satisfying πQ
∗
= 0 with πe = 1
(Stol,2004) by, for j = 0,1,2,··· ,K
∗
2
,
π = (π
0
,π
1
,π
2
,··· ,π
K
∗
2
) with π
j
= (π
j1
,π
j2
).
Then the required probability q
1, j
is given by
q
1, j
=
(
π
j
Λe/C, j = 0, 1, ··· ,N
2
− 1,
π
j
Λ
2
e/C, j = N
2
,N
2
+ 1,··· ,K
∗
2
,
where C =
N
2
−1
∑
l=0
π
l
Λe+
K
∗
2
∑
l=N
2
π
l
Λ
2
e. Moreover let r
j
be
the ratio that the number of A customers served by
generalists is j, then we have
r
j
= π
j
Λ
I
e/C, j = 0, 1, 2, · ·· ,N
2
. (7)
3.4 To Get p
2,i
≡ P(X
1
= i|N
2
≤ X
2
≤ K
∗
2
)
Given that {N
2
≤ X
2
≤ K
∗
2
}, all generalists are busy,
the generalists are either serving B customers or are
serving A customers only when B queue is empty. A
customers are served by the N
1
specialists with each
service rate µ
1
. When all specialists are busy, A cus-
tomers only see a generalist if there is no B customer
in B queue(X
2
= N
2
). In this case, a service comple-
tion by a generalist diverts a customer from A queue
to the generalist.
On the other hand, An arriving B customer is first
served by the N
2
generalists with each service rate
µ
2
. When all generalists are busy B customers are
waiting in B queue. In addition, when A customers
are waiting in A queue, a single server is sometimes
available with service rate N
2
µ
2
. This server expe-
riences random periods of unavailability and these
breakdowns correspond to the busy periods of the
M/M/1/K
∗
2
+ M queue. Here K
∗
2
is a random vari-
able, which depends on the number of generalists
occupied by A customers. The busy periods of the
M/M/1/K
∗
2
+ M queue with the parameters λ
2
, N
2
µ
2
and θ
2
are approximated by a hyperexponential distri-
bution with parameters that match the first three mo-
ments of the busy periods(Shum,2004).
Let L(t) be the number of customers at time t in
the submodel and let τ be the length of the busy pe-
riod. Then we have to find the following Laplace
transform, on |x| ≤ 1, s > 0,
φ
n
(s) = E[e
−st
|L(0) = n], n = 1,2,··· ,K, (8)
where the boundary conditions are φ
K
∗
2
+1
(s) = φ
K
∗
2
(s)
and φ
0
(s) = 1. After all, φ
1
(s) is the required Laplace
transform. Conditioning on the epoch of customer’s
first arrival, departure or reneging(whichever occurs
first), we can easily find φ
1
(s).
Now to approximate the busy period distribution,
define h(τ) as follows
h(τ) = αγ
1
e
−γ
1
τ
+ (1− α)γ
2
e
−γ
2
τ
, (9)
where τ,α,γ
1
and γ
2
are non-negative. The follow-
ing parameters match the first three moments of the
hyperexponential distribution with the three moments
m
1
, m
2
and m
3
of φ
1
(s) (Shum,2004).
γ
1
,γ
2
=
v
1
±
q
v
2
1
− 4v
2
2
, α =
γ
1
(1− γ
2
m
1
)
γ
1
− γ
2
, (10)
where v
1
and v
2
are given by
v
2
=
6m
2
1
− 3m
2
(3/2)m
2
2
− m
1
m
3
, v
1
=
1
m
1
+
m
2
v
2
2m
1
.
Let’s return to finding p
2,i
. 1) First, when
there are A customers in A queue(X
1
> N
1
), only if
X
2
= N
2
, the corresponding queueing system is gov-
erned by both M/M/1/(K
∗
2
− N
1
+ 1) + M queue and
M/G
1
/1/(K
∗
2
− N
1
+ 1) + M queue with the arrival
rate λ
1
and the hyperexponential service time given in
(9). 2) Secondly, given that {X
1
≤ N
1
}, A customers
are served by the N
1
specialists. The correspond-
ing queueing system is modeled as the M/M/N
1
/N
1
queue with the arrival rate λ
1
and the service rate µ
1
.
At first, we consider the case 1). Given that X
1
=
i > N
1
, the specialist serves A customers with expo-
nential service time with mean (N
1
µ
1
)
−1
. If we con-
sider reneging, then we can conceive that the result-
ing service time distribution is B ∼ Exp(N
1
µ
1
+ θ
1
).
Furthermore, the generalist serves A customers with
the hyperexponential service time (H ∼ h(x)) given
in (9). Consequently, A customers complete their
service with the minimum time of B and H. So
the corresponding queueing system is modeled as the
M/G
2
/1/(K
∗
2
− N
1
+ 1) + M queue.
Note that by PASTA, the number of customers in
the system at an arbitrary time is equal to the number
of customers at an arrival epoch(Taga,1993). Then we
have, for 0 ≤ i ≤ K
∗
2
− N
1
− 1,
p
2,i+N
1
=
π
i+1
π
0
+ λ
1
/(γ+ θ
1
+ N
1
µ
1
)
,
p
2,K
∗
2
= 1−
1
π
0
+ λ
1
/(γ+ θ
1
+ N
1
µ
1
)
,
ICE-B 2007 - International Conference on e-Business
48

where γ = αγ
1
+ (1− α)γ
2
is given by (10).
For the case 2), the corresponding queueing sys-
tem is the M/M/N
1
/N
1
queue. By the normalization
condition including the above equations, we have
p
2,i
=
1
i!

λ
1
µ
1

i
1−
K
∗
2
∑
i=N
1
+1
p
2,i
!

N
1
∑
j=0
1
j!

λ
1
µ
1

j
.
3.5 Performance Measures
When we know the probabilities {p
1,i
}, {p
2,i
}, {q
1, j
}
and {q
2, j
}, by the conditional probability, we can eas-
ily get the probabilities P(X
1
= i), i = 0,1,··· ,K
∗
1
and
P(X
2
= j), j = 0,1,··· ,K
∗
2
. By the probability (7), the
mean queue lengths of queues A and B are given by
K
A
= K
1
− N
1
−
N
2
∑
j=1
jr
j
, K
B
= K
2
− N
2
+
N
2
∑
j=1
jr
j
.
The blocking probabilities for the mean queue lengths
K
A
and K
B
are given by
P
A
= P(X
1
= K
A
+ N
1
), P
B
= P(X
2
= K
B
+ N
2
).
Given that the mean queue lengths are K
A
and K
B
, the
mean waiting times are given by
W
qA
=
1
λ
1
(1− P
A
)
K
A
+N
1
∑
i=N
1
+1
(i− N
1
)P(X
1
= i),
W
qB
=
1
λ
2
(1− P
B
)
K
B
+N
2
∑
j=N
2
+1
(i− N
2
)P(X
2
= j).
4 NUMERICAL RESULTS
In this section, we present some numerical results to
show the effect of the system parameters in our N-
design call center on the performance measures such
as the mean waiting time and the blocking probabil-
ity. We let K
1
= 70 and K
2
= 50 be two fixed numbers
of telephone lines for two types of customers respec-
tively. We choose N
1
= 30 agents and N
2
= 40 agents
as the fixed numbers of the specialists and general-
ists, respectively. We vary customers’ arrival rates
per minute λ
1
and λ
2
in order to get the proper uti-
lizations(traffic intensities).
We assume that the generalist needs more time
to serve a particular customer than the specialist.
In general, customer’s mean service time varies be-
tween 60 and 180 seconds(Mand,2005; Stol,2004).
Hence agents’s service rates µ
1
and µ
2
vary between
1 and 1/3. We can usually select θ
−1
1
and θ
−1
2
be-
tween 120 and 240 seconds as the mean values of the
exponentially distributed patient times(Mand,2004;
Gans,2003). We take the fixed values µ
−1
1
= 2, µ
−1
2
=
3, θ
−1
1
= 2 and θ
−1
2
= 4 minutes as some system pa-
rameters in Figs. 2 and 3.
5 10 15 20 25
−0.05
0
0.05
0.1
0.15
0.2
Arrival rate of A−customer (calls/min))
Blocking probability of A−customer
Arrival rate of B−customer:10, 15, 20, 25 calls/min
lam2=10
lam2=15
lam2=20
lam2=25
Figure 2: A customer’s P
A
vs. A customer’s arrival rate.
5 10 15 20 25
0
5
10
15
20
25
30
35
Arrival rate of A−customer (calls/min)
Mean waiting time in B−queue
Arrival rate of B−customer:10, 15, 20, 25 calls/min
lam2=10
lam2=15
lam2=20
lam2=25
Figure 3: W
qB
in B queue vs. A customer’s arrival rate.
Fig. 2 shows the blocking probability(P
A
) of A
customer’s calls when A customer’s arrival rate varies
from 4 to 28 per minutes. The blocking probability is
well calculated in Section 3.5. We can see that when
A customer’s arrival rate increases, the blocking prob-
ability of A customer’s calls increases exponentially
in case that A customer’s arriving rate is fixed. When
B customer’s arrival rate is high(lam2=20, 25), the
blocking probability of A customer’s calls decreases
according to B customer’s arrival rate. The reason is
as follows. While B customer’s arrival rate is high,
if the number of A customers holding the general-
ists decreases, the mean length of A queue increases.
Thus the blocking probability of A customer’s calls
decreases.
Fig. 3 shows B customer’s mean waiting time
(W
qB
) in B queue when A customer’s arrival rate
varies. The waiting time is well derived in Section
3.5. We can see that when A customer’s arrival rate
APPROXIMATE ANALYSIS OF A CALL CENTER WITH SKILL-BASED ROUTING
49

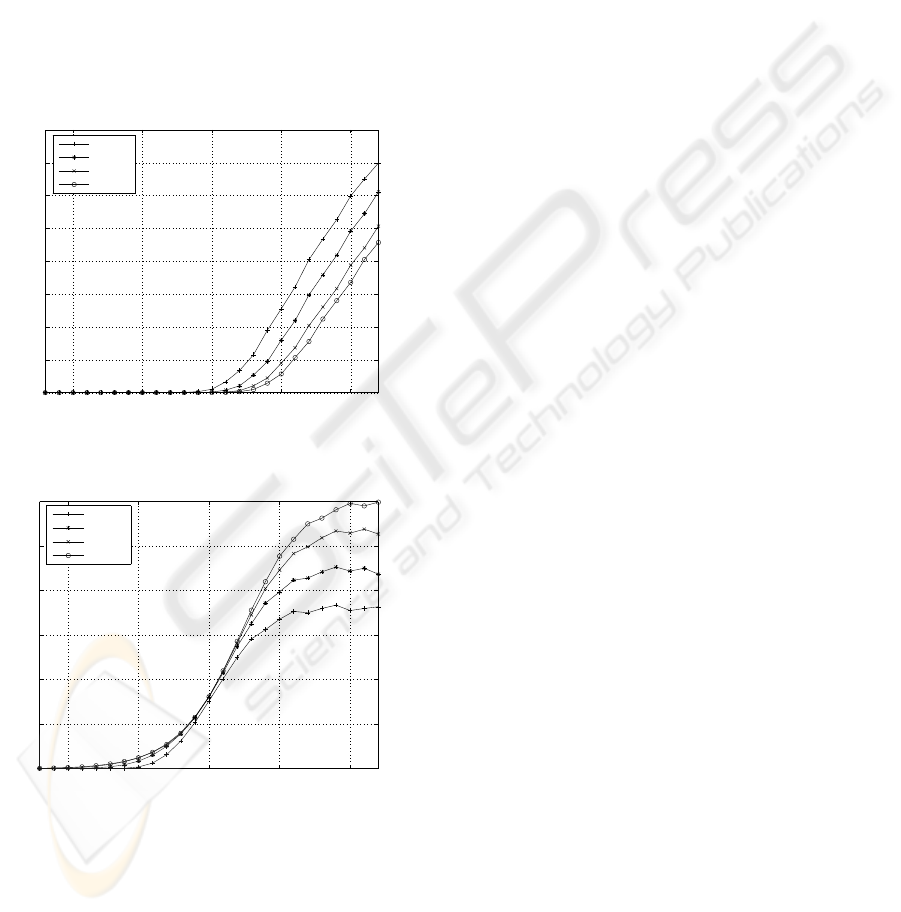
increases, the mean waiting time of B customer con-
tinues to increase.
From now on, we investigate the performance
measures when B customer’s arrival rate λ
2
varies but
A customer’s arrival rate λ
1
is fixed. The 5 cases of
A customer’s arrival rates are considered. We take the
fixed values µ
−1
1
= 2, µ
−1
2
= 3, θ
−1
1
= 2 and θ
−1
2
= 4
minutes as some system parameters in Figs. 4 and 5.
Fig. 4 shows the blocking probability(P
B
) of B cus-
tomer’s calls when B customer’s arrival rate varies.
We can see that when B customer’s arrival rate in-
creases, the blocking probability of B customer’s calls
increases in case that A customer’s arriving rate is
fixed.
5 10 15 20 25
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Arrival rate of B−customer (calls/min)
Blocking probability of B−customer
Arrival rate of A−customer:10, 15, 20, 25 calls/min
lam1=10
lam1=15
lam1=20
lam1=25
Figure 4: B customer’s P
B
vs. B customer’s arrival rate.
5 10 15 20 25
0
5
10
15
20
25
30
Arrival rate of B−customer (calls/min)
Mean waiting time in B−queue
Arrival rate of A−customer:10, 15, 20, 25 calls/min
lam1=10
lam1=15
lam1=20
lam1=25
Figure 5: W
qB
in B queue vs. B customer’s arrival rate.
Fig. 5 shows B customer’s mean waiting time
(W
qB
) in B queue when B customer’s arrival rate
varies. We can see that when B customer’s arrival
rate increases, the mean waiting time of B customer
continues to increase. We also see that the behavior of
the mean waiting time is similar to that of the ordinary
queueing systems, when the arrival rate is low.
ACKNOWLEDGEMENTS
This research was supported by the MIC, Korea, un-
der the ITRC support program supervised by the IITA.
REFERENCES
Mandelbaum, A., & Zeltyn, S. (2005). Service Engineer-
ing in Action: The Palm/ Erlang-A Queue, with Ap-
plications to Call Centers. Israeli Science Foundation
Research Report.
Borst, S., Mandelbaum, A., & Reiman, M.I. (2004). Dimen-
sioning Large Call Centers. Operations Research, 52,
17-34.
Stolletz, R., & Helber, S. (2004). Performance analysis of
an inbound call center with skills-based routing. OR
Spectrum, 26, 331-352.
Shimkin, M., & Mandelbaum, A. (2004). Rational Aban-
donment from Tele-Queues: Nonlinear Waiting Costs
with Heterogeneous Preferences. Queueing Systems,
47, 117-146.
Mandelbaum, A., & Zeltyn, S. (2004). The impact of cus-
tomer’s patience on delay and abandon ment: some
empirically-driven experiments with the M/M/n+G
queue. OR Spectrum, 26, 377-411.
Gans, N., Koole, G., & Mandelbaum, A. (2003). Commis-
sioned Paper, Telephone Call Centers: Tutorial, Re-
view, and Research Prospect. Manufacturing & Sci-
ence Operations Management, 5, 79-141.
Stolletz, R. (2003). Performance analysis and optimization
of inbound call centers. Lecture Notes in Economics
and Mathematical systems, 528.
Shumsky, R.A. (2004). Appoximation and analysis of a call
center with flexible and specialized servers. OR Spec-
trum, 26, 307-330.
Gross, D., & Harris, C.H. (1985). Fundamentals of Queue-
ing Theory. John Wiley & Sons, Inc.
Garnett, O., Mandelbaum, A., & Reiman, M. (2002). De-
signing a Call Center with Impatient Customers. Man-
ufacturing and Science Operations Research, 4, 208-
227.
Kukzura, A. (1973). The interrupted poisson process as an
overflow process. Bell System Technical Journal, 52,
437-448.
Onvural, R.O. (1975). Asychronous Transfer Mode Net-
works: Performance Issues. Second edition, Artech
House.
Heffes, H., & Lucantony, D.M. (1986). A Markov modu-
lated characterization of packetized voice, data traffic
and related statistical multiplexer performance. IEEE
J. Selected Areas Comm., 4, 856-868.
Tagaki, H. (1993). Queueing Analysis, Vol. 2: Finite Sys-
tems. IBM Japan, Ltd., North-Holland.
ICE-B 2007 - International Conference on e-Business
50