OPTIMIZING REVENUE
Service Provisioning Systems with QoS Contracts
J. Palmer, I. Mitrani, M. Mazzucco
School of Computing Science, Newcastle University, NE1 7RU, UK
P. McKee, M. Fisher
BT Group, Adastral Park, Ipswich, IP5 3RE, UK
Keywords:
Quality of service, Revenue maximization, Server allocation, Admission policies, M/M/N/K queue.
Abstract:
We consider the problem of how best to structure and control a distributed computer system containing many
processors, subject to Quality of Service contracts. Services of different types are offered, with different
charges for running jobs and penalties for failing to meet the QoS requirements. The aim is to choose the
number of servers allocated to each service type, and the admission criteria for jobs of that type, so as to
maximize the total average revenue per unit time. The performance of a fast allocation heuristic is evaluated.
1 INTRODUCTION
The context for this work is a service provisioning
system where a cluster of resources (servers) is em-
ployed to offer different services to a community
of users. The immediate motivation came from the
world of web services, but other multi-class hosting
environments would fall in the same framework. With
each service type is associated a service level agree-
ment (SLA), formalizing the obligations of the users
and the provider. In particular, a user agrees to pay a
certain amount for each accepted and completed job,
while the provider agrees to pay a penalty whenever
the response time (or waiting time) of a job exceeds a
certain bound. It is then the provider’s responsibility
to decide how to allocate the available resources, and
when to accept jobs, in order to make the system as
profitable as possible. That, in general terms, is the
problem that we wish to address.
In order to do that, it is necessary to have a quan-
titative model of user demand, service provision and
admission policy. We use, as a basic building block,
the M/M/N/K queueing model, augmented with the
economic parameters of charges and penalties. The
aim of this paper is to propose and evaluate efficient
and easily implementable policies for resource allo-
cation and job admission.
The approach we have adopted includes mathe-
matical analysis, numerical solutions and also experi-
mentation with a real hosting environment where dif-
ferent web services are requested and deployed.
The economic issues arising in multi-server,
multi-class systems with QoS contracts based on re-
sponse times or waiting times do not appear to have
been studied before. Huberman et al (Huberman
et al., 2005) describe a pricing structure for service
provision which ensures truthful reporting of QoS by
providers. However, that paper assumes that the prob-
ability of providing a particular level of QoS is fixed
and known, without being specific about how QoS is
measured. The distribution of response or waiting
times is not considered. Rajkumar et al (Rajkumar
et al., 1997) consider a resource allocation model for
QoS management, where application needs may in-
clude timeliness, reliability, security and other appli-
cation specific requirements. The model is described
in terms of a utility function to be maximised. This
model is extended in (Ghosh et al., 2003) and (Hansen
et al., 2004). Such multi-dimensional QoS is beyond
the scope of this paper. However, although the model
described by Rajkumar et al allows for variation in
job computation time and frequency of application
requests, once again the distribution of the response
times and/or waiting times is not considered.
The model assumptions are described in section
2. The revenue analysis is carried out in section 3.
Numerical results and observations gathered from a
working web service hosting system are presented in
187
Palmer J., Mitrani I., Mazzucco M., McKee P. and Fisher M. (2007).
OPTIMIZING REVENUE - Service Provisioning Systems with QoS Contracts.
In Proceedings of the Second International Conference on e-Business, pages 187-191
DOI: 10.5220/0002111501870191
Copyright
c
 SciTePress

section 4. Section 5 contains a summary and conclu-
sions.
2 THE MODEL
The system consists of N identical servers, which may
be used to serve jobs belonging to m different types.
However, once allocated to a type of service, a server
remains dedicated to jobs of that type only. In other
words, a static and non-sharing server allocation pol-
icy is employed: n
i
servers are assigned to jobs of type
i (n
1
+n
2
+... +n
m
= N). Such a policy may deliber-
ately take the decision to deny service to one or more
job types (this will certainly happen if the number of
services exceeds the number of servers).
Jobs of type i arrive according to an indepen-
dent Poisson process with rate λ
i
, and join a separate
queue. Their required service times are distributed
exponentially with mean 1/µ
i
. An admission policy
controlled by a set of thresholds is in operation: if
there are K
i
jobs of type i present in the system (wait-
ing and in service), then incoming type i jobs are not
accepted and are lost (i = 1,2, ...,m).
For the purposes of this model, the quality of
service experienced by an accepted job is measured
either in terms of its response time, W (the inter-
val between the job’s arrival and completion), or in
terms of its waiting time, w (excluding the service
time). Whichever the chosen measure, it is mentioned
explicitly in a service level agreement between the
provider and the users. We assume that each such
contract would include the following three clauses:
1. Charge: For each accepted and completed job of
type i a user shall pay a charge of c
i
(in practice
this may be proportional to the average length of
type i jobs).
2. Obligation: The response time, W
i
(or waiting
time, w
i
), of an accepted job of type i shall not
exceed q
i
.
3. Penalty: For each accepted job of type i whose
response time (or waiting time) exceeds q
i
, the
provider shall pay to the user a penalty of r
i
.
Thus, in this model, service type i is characterized
by its ‘demand parameters’ (λ
i
,µ
i
), and its ‘economic
parameters’, namely the triple
(c
i
,q
i
,r
i
) = (charge,obligation, penalty) (1)
Within the control of the provider are the server
allocations, n
i
, and the admission thresholds, K
i
. The
objective is to choose those allocations and thresholds
so as to maximize the total average revenue earned per
unit time in the steady state. A stationary regime al-
ways exists for a bounded queue, but if K
i
= ∞ for
some i, then the corresponding demand parameters
must satisfy λ
i
< n
i
µ
i
in order that the queue be stable.
Note that, although we make no assumptions
about the relative magnitudes of the charge and
penalty parameters, the more interesting case is where
the latter is at least as large as the former: c
i
≤ r
i
.
Otherwise one could guarantee a positive revenue by
accepting all jobs of type i, regardless of the load and
of the obligation made.
3 REVENUE EVALUATION
We concentrate first on the subsystem associated with
service i, for a given set of demand and economic
parameters, and fixed allocation n
i
and threshold K
i
.
That subsystem behaves like an M/M/n
i
/K
i
queue
(see, for example, (Mitrani, 1998)).
Denote by V
i
the average revenue earned from
type i jobs per unit time in the steady state. If the
QoS measure is the response time, then V
i
is given by
V
i
= λ
i
K
i
−1
∑
j=0
p
i, j
[c
i
− r
i
P(W
i, j
> q
i
)] , (2)
where p
i, j
is the stationary probability that there are j
jobs of type i in the M/M/n
i
/K
i
queue, andW
i, j
is the
response time of a type i job which finds, on arrival, j
other type i jobs present.
If the QoS measure is the waiting time, then V
i
is
given by a similar expression, with P(W
i, j
> q
i
) be-
ing replaced by P(w
i, j
> q
i
) (where w
i, j
is the waiting
time of a type i job which finds, on arrival, j other
type i jobs present).
The stationary distribution of the number of type
i jobs present is found by solving the balance and
normalizing equations. Similarly, the probabilities
P(W
i, j
> q
i
) can be evaluated by computing the dis-
tribution function of a convolution of the right num-
ber of exponential distributions. This can be done in
closed form.
When the computation of V
i
is done for different
sets of parameter values, it becomes clear that it is
a unimodal function of K
i
. That is, it has a single
maximum, which may be at K
i
= ∞ for lightly loaded
systems. We do not have a mathematical proof of
this proposition, but have verified it in numerous nu-
merical experiments. That observation implies that
one can search for the optimal admission threshold
by evaluating V
i
for consecutive values of K
i
, stop-
ping either when V
i
starts decreasing or, if that does
not happen, when the increase becomes smaller than
some ε. Such searches are typically very fast.
ICE-B 2007 - International Conference on e-Business
188

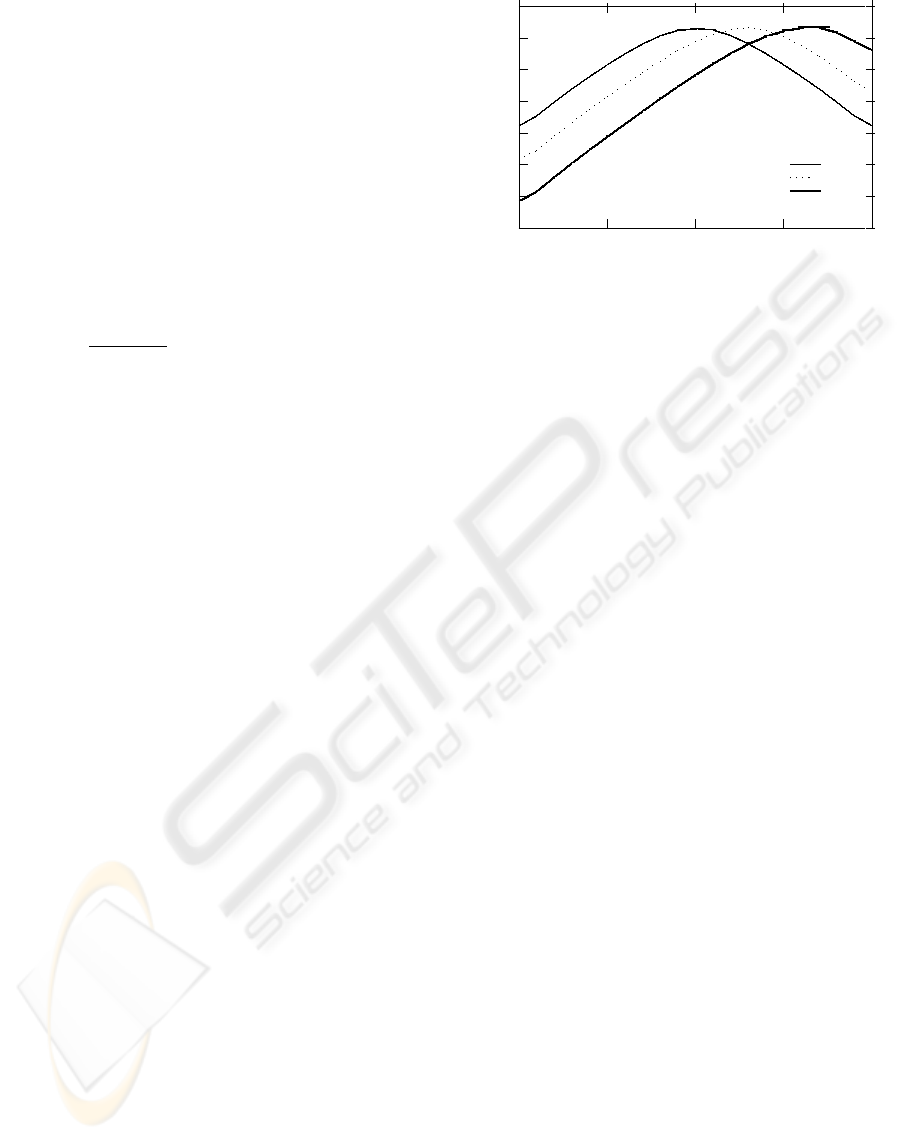
The second problem under consideration is to
maximize the total average profit per unit time, V,
earned from all the m different service types:
V = V
1
+V
2
+ ... +V
m
(3)
The server allocations vector, (n
1
,n
2
,. ..,n
m
) (satisfy-
ing n
1
+n
2
++n
m
= N), and the admission thresholds
vector, (K
1
,K
2
,. ..,K
m
), must be chosen so as to max-
imize V.
A simple and intuitively sensible policy is to al-
locate the servers roughly in proportion to the offered
load, ρ
i
= λ
i
/µ
i
, and to the service charge, c
i
, for each
type. In other words, set
n
i
=
$
N
ρ
i
c
i
∑
m
j=1
ρ
j
c
j
+ 0.5
%
(i = 1,..., m− 1) ;
n
m
= N −
m−1
∑
i=1
n
i
(4)
(adding 0.5 and truncating is the round-off operation).
The corresponding vector of optimal admission
thresholds is determined as described above, at a com-
putational cost on the order of O(m). This will be re-
ferred to as the ‘heuristic’ policy. Note that it may
yield an allocation of n
i
= 0 and an admission thresh-
old K
i
= 0 for some service types. If that is unde-
sirable for reasons other than revenue, the allocations
can be adjusted appropriately.
4 NUMERICAL AND EMPIRICAL
RESULTS
Several experiments were carried out, aiming to eval-
uate the benefits of determining the optimal system
configuration. To reduce the number of variables, the
following features were held fixed:
• The QoS measure is the response time, W.
• The obligations undertaken by the provider are
that jobs will complete within twice their average
required service times, i.e. q
i
= 2/µ
i
.
• All penalties are equal to the corresponding
charges: r
i
= c
i
(i.e., if the response time exceeds
the obligation, users get their money back).
The first experiment concerns a 20-server system
offering two services (N = 20, m = 2). The 21 possi-
ble server allocations (n
1
,n
2
) are evaluated and com-
pared, for three different pairs of arrival rates. In each
case, the total offered load is ρ
1
+ ρ
2
= 15.0, which
means that the 20-server system is 75% loaded.
The average service times and job charges are
1/µ
1
= 1/µ
2
= 1.0 and c
1
= c
2
= 100.0, respectively.
0
20
40
60
80
100
120
140
0 5 10 15 20
revenue, V
servers allocated to job type 2
λ
1
= 0.75, λ
2
= 0.75
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
⋄
λ
1
= 0.5, λ
2
= 1.0
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
λ
1
= 0.2, λ
2
= 1.3
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
Figure 1: Maximum revenue earned for different server al-
locations: N = 20, m = 2, c
i
= r
i
= 100, µ
i
= 0.1.
For each server allocation, the optimal pair of admis-
sion thresholds is determined and used.
Figure 1 shows the total revenue earned, V =
V
1
+ V
2
, as a function of n
2
. When the two arrival
rates are equal, λ
1
= λ
2
= 7.5, the demand is symmet-
ric and so the optimal allocation is n
1
= n
2
= 10. The
optimal admission thresholds are K
1
= K
2
= 19. For
asymmetric demands, as one might expect, it is bet-
ter to allocate more servers to the more heavily loaded
service. Thus, if λ
1
= 5 and λ
2
= 10, the optimal allo-
cation is n
1
= 7, n
2
= 13, with admission thresholds
K
1
= 14, K
2
= 24. Lastly, when λ
1
= 2 and λ
2
= 13,
the optimal allocation is n
1
= 4, n
2
= 16, with admis-
sion thresholds K
1
= 9, K
2
= 28.
It is worth noting that the optimal server alloca-
tions are quite close to those suggested by the heuris-
tic described in the last section.
The aim of the next experiment is to evaluate the
quality of the heuristic allocation policy. A 20-server
system with 2 types of service was subjected to fluc-
tuating demand controlled by a single parameter, λ.
During a period of time of length 1000, jobs of type
1 and 2 arrive at rates λ
1
= λ and λ
2
= 10λ, respec-
tively. Then, during the next period of length 1000,
the arrival rates are λ
1
= 10λ and λ
2
= λ, respectively;
and so on. The average service times for the two
types are equal, 1/µ
1
= 1/µ
2
= 0.8, as are the charges,
c
1
= c
2
= 100. In addition, a third policy which uses
the same server allocations as the heuristic, but does
not restrict admissions (i.e., K
1
= K
2
= ∞), is included
in the comparison. In all cases, it is assumed that, at
the beginning of every new period, the demand pa-
rameters become known instantaneously, so that the
server allocations and admission thresholds can be
computed and applied during that period. In order
to avoid the question of whether the system reaches
steady state during each period, the comparisons were
done by simulation.
In figure 2, the total revenue earned per unit time
by the three policies is plotted against the offered load
OPTIMIZING REVENUE - Service Provisioning Systems with QoS Contracts
189

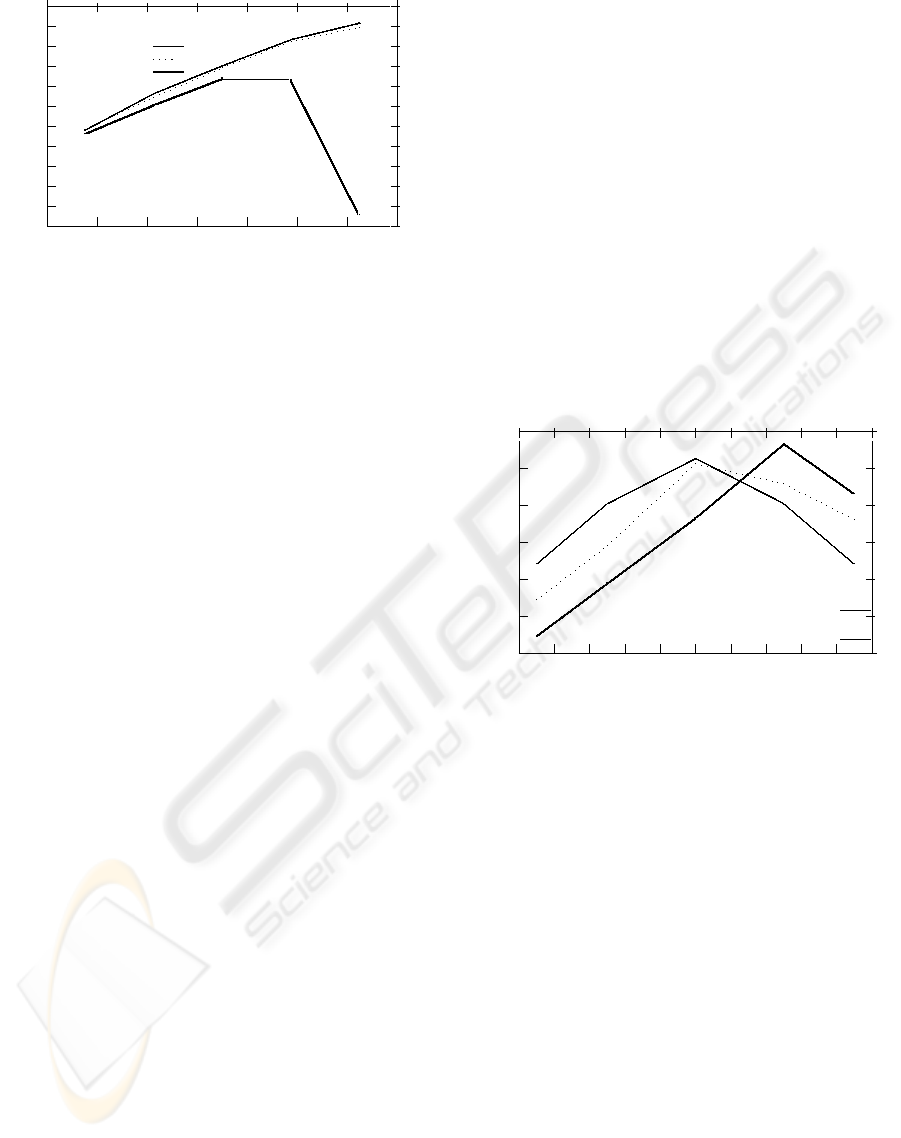
700
750
800
850
900
950
1000
1050
1100
1150
1200
1250
65 70 75 80 85 90 95 100
revenue, V
load
optimal
⋄
⋄
⋄
⋄
⋄
⋄
heuristic
+
+
+
+
+
+
admit all
c
c
c
c
c
c
Figure 2: Policy comparisons: revenue as function of load:
N = 20,µ
i
= 0.8, c
i
= r
i
= 100.
(which is equal to 11λ/µ
1
). The near-optimality of
the heuristic is rather remarkable. In contrast, the rev-
enues earned by the unrestricted admission policy in-
crease more slowly, and then drop sharply as the load
becomes heavy. This example demonstrates that, by
itself, a sensible server allocation is not enough; to
yield good results, it should be accompanied by a sen-
sible admission policy.
Realization of a Hosting System
A middleware platform for the deployment and use
of web services was designed and implemented, with
the aim of providing a real-life environment in which
to study various QoS policies. The architecture is
message-based and asynchronous.
Client requests for services arrive at a controller
which collects statistics, estimates parameters and im-
plements the server allocation and job admission poli-
cies. The controller makes reconfiguration decisions
(e.g., server reallocations or changes of admission
thresholds) at intervals of specified length. There is
a handler associated with each service type, whose
responsibilities include (a) deployment of the service
(fetched from the code store) if not already deployed,
(b) queueing of accepted jobs, if necessary, and (c)
passing to the controller all necessary statistics.
An experiment similar to the one illustrated in fig-
ure 1 was carried out using a cluster of 20 comput-
ers. Two service types were deployed, and streams
of requests were generated. Note that this was not an
emulation of the model, but a real implementation. In
the real system, messages passed between client, con-
troller, handler and server are subject to network de-
lays and processing overheads, which cannot be con-
trolled. Also, it could not be guaranteed that the com-
puters were dedicated to these tasks; there could be
random demands from other users.
The three pairs of arrival rates used in this exper-
iment were the same as in figure 1: λ
1
= λ
2
= 0.75;
λ
1
= 0.5, λ
2
= 1.0; and λ
1
= 0.2, λ
2
= 1.3. The aver-
age service times were also the same: 1/µ
1
= 1/µ
2
=
10. However, because of the factors mentioned above,
one should not expect a precise match between the
numerical predictions and the observations of the real
system. In figure 3, the total revenues earned are plot-
ted against n
2
, the number of servers allocated to ser-
vice 2. Each point in the figure corresponds to a sepa-
rate run of the system, during which about 1000 jobs
of each type arrived and were completed. These plots
have the same general characteristics as the ones in
figure 1. The maximum achievable revenue is again
about 120 per unit time, and the server allocations that
achieve it are the same, with one exception. In the
case of λ
1
= 0.5, λ
2
= 1.0, the real system earned its
highest revenue for n
1
= 10, n
2
= 10, whereas the nu-
merical calculations suggested n
1
= 7, n
2
= 13. How-
ever, the differences in revenues are not large.
20
40
60
80
100
120
140
0 2 4 6 8 10 12 14 16 18 20
revenue, V
servers allocated to type 2
λ
1
= 0.75, λ
2
= 0.75
⋄
⋄
⋄
⋄
⋄
⋄
λ
1
= 0.5, λ
2
= 1.0
+
+
+
+
+
+
λ
1
= 0.2, λ
2
= 1.3
c
c
c
c
c
c
Figure 3: Observed revenues for different server alloca-
tions: N = 20, m = 2, c
i
= r
i
= 100.
5 CONCLUSIONS
The contribution of this paper is to introduce quantita-
tive methods to a previously unexplored area, namely
the market in computer services. We have demon-
strated that policy decisions such as server allocations
and admission thresholds can have a significant ef-
fect on the revenue earned. Moreover, those decisions
are affected by the contractual obligations between
clients and provider in relation to quality of service.
When the numbers of services offered and servers
available are too large for an exhaustive search of the
optimal policy, a simple heuristic is proposed. Exper-
imentation suggests that it is close to optimal.
ACKNOWLEDGEMENTS
This work was carried out as part of the research
project QOSP (Quality Of Service Provisioning),
ICE-B 2007 - International Conference on e-Business
190

funded by British Telecom. It was also supported by
the European Union Network of Excellence EuroNGI
(Next Generation Internet).
REFERENCES
Ghosh, S. et al. (2003). Scalable resource allocation for
multi-processor qos optimization. In The Interna-
tional Conference on Distributed Computing Systems.
Hansen, J. et al. (2004). Resource management of highly
configurable tasks. In IPDPS ’04, The 18th Inter-
national Parallel and Distributed Processing Sympo-
sium, pages 116–123.
Huberman, B. A. et al. (2005). Ensuring trust in one
time exchanges: solving the qos problem. Netnomics,
7:27–37.
Mitrani, I. (1998). Probabilistic Modelling. Cambridge
University Press.
Rajkumar, R. et al. (1997). A resource allocation model for
qos management. In RTSS ’97, The 18th IEEE Real-
Time Systems Symposium, pages 298–307.
OPTIMIZING REVENUE - Service Provisioning Systems with QoS Contracts
191