CUSTOMER BEHAVIOR MODELING UNDER SEVERAL

DECISION-MAKING PROCESSES BY USING EM ALGORITHM

Takeshi Kurosawa, Ken Nishimatsu, Motoi Iwashita

NTT Service Integration Laboratories, 3-9-11 Midori-Cho, Musashino, Tokyo, Japan

Akiya Inoue

Department of Management Information Science, Chiba Institute of Technology,2-17-1 Tsudanuma,Narashino ,Chiba, Japan

Keywords:

Discrete Choice Analysis, EM-Algorithm, Decision Making Process, Consumer Behavior, Data and Knowl-

edge Engineering.

Abstract:

This paper gives a model of customer choice behavior modeling based on a combination of decision-making

processes by applying latent class model based on EM algorithm. This model can apply for the choice prob-

lems of multi services and multi brands under various decision-making processes. In addition to the model

based on EM algorithm, we tried some conventional models and compared them. The model based on EM

algorithm enables us to know what kinds of customers are classiﬁed into a certain class. Moreover, we could

construct more accuracy model than conventional model and found the existence of two decision-making

processes.

1 INTRODUCTION

The amount of the trafﬁc ﬂowing in the network de-

pends on the number of customers. Therefore the

estimation of the number of customers is very im-

portant factor in the network design. Generally cus-

tomer choice behavior modeling is very complicated.

These days, customers are faced with a wide range of

choice for telecommunications services. This arises

from the rapid progress of information and communi-

cation technology and the competitive environment.

Therefore, customers use various different decision-

making processes to select a service that provides

the features they want. Here, the decision-making

process means the order of selection when the cus-

tomer chooses the service. However, we generally

cannot know what kind of decision-making process

they are using. In such a situation, we cannot fully

express customer choice behavior by using model

whose structure is based on a single decision-making

process. Therefore, a model that takes into consider-

ation a customer’s complicated decision-making pro-

cesses is needed. Main purpose of this paper is to

give customer choice behavior modeling under sev-

eral decision-making processes because the accuracy

of the customer choice behavior modeling gives us

more accuracy trafﬁc estimation and service demand

estimation.

For this purpose, we use a latent class model using

the EM algorithm. We regard a decision-making pro-

cess as one latent class of EM algorithm. One class

model is expressed by the hierarchy structure. In this

paper, we explain our model and present results that

verify it.

2 RELATED WORK

The telephone service market is ﬁercely competitive.

Both the telephone service and Internet service mar-

kets are changing rapidly as technology progresses.

Therefore, it is not always appropriate to forecast ser-

vice demand by using conventional time series anal-

ysis based on measurement data obtained in network

management systems. Some researchers have studied

markets such as Internet service (Savage and Wald-

man, 2004; Loomis and Taylor, 2001) and telephone

services (Fildes and Kumar, 2002; Loomis and Tay-

lor, 1999). These described to only one service model.

We have proposed the technique of Scenario Sim-

ulation (Inoue et al., 2003a; Inoue et al., 2003b;

Nishimatsu et al., 2004; Takahashi et al., 2004; Nishi-

339

Kurosawa T., Nishimatsu K., Iwashita M. and Inoue A. (2007).

CUSTOMER BEHAVIOR MODELING UNDER SEVERAL DECISION-MAKING PROCESSES BY USING EM ALGORITHM.

In Proceedings of the Second International Conference on e-Business, pages 339-346

DOI: 10.5220/0002115703390346

 SciTePress

matsu et al., 2005; Nishimatsu et al., 2006), which

uses customer choice behavior modeling. This mod-

eling (See the appendix A.1) is used to estimate the

demand for a service and the amount of trafﬁc that

will ﬂow through the network. Therefore, enhancing

the accuracy of customer choice behavior modeling is

the most important factor in Scenario Simulation.

Usually, we use Discrete Choice Analysis (Ben-

Akiva and Lerman, 1985; Train, 2003)(DCA) to con-

struct a customer choice behavior model. DCA (See

the appendix A.2) is the technique derived from the

ﬁeld of trafﬁc engineering and it is applied in vari-

ous ﬁelds. Customer choice behavior modeling for

a telecommunications service has been analyzed us-

ing DCA (Kurosawa et al., 2005; Kurosawa et al.,

2006). One reason for the complexity of the tele-

phone market is that a customer can get the features

he/she wants by combining multiple services. For ex-

ample, a customer who wants to use IP telephony may

make separate contracts with an Internet access line

provider, an Internet service provider (ISP), and an IP

telephony provider. This combination of services can

more economical for Internet users than using POTS

(plain old telephone service). A nested structure can

express the priority or the order of selecting. We can

consider the priority or the order of selecting as a

decision-making process. To solve the problem, cus-

tomer choice behavior modeling using a nested struc-

ture was examined (Kurosawa et al., 2006). That ex-

amination showed the existence of a decision-making

process with a nested structure. The paper concluded

that one decision-making process is more appropri-

ate than other models. The research (Ben-Akiva and

Gershenfeld, 1998) focused on the combination of op-

tional services. However, customers do not always all

use the same decision-making process. Namely, two

or more decision-making processes may exist. How-

ever, we cannot know which decision-making process

a given customer will use. To handle this characteris-

tic, we focused on the EM algorithm. This algorithm

complements imperfect data by using expected val-

ues obtained through the application of Bayes’ the-

ory. That is, posterior probability is used as the ex-

pected value. This framework is used for the latent

class model. Generally, we cannot know which kind

of latent class the customer belongs to. So the EM al-

gorithm obtains the probability of belonging to a class

by using an expected value.

In this case study, we veriﬁed the accuracy of our

model. And we focused on what kinds of customers

are classiﬁed into a certain class (decision-making

process) because the class model has individual vari-

ables.

3 CHOICE MODEL UNDER

VARIOUS DECISION-MAKING

PROCESSES

We use DCA models in each step of the EM al-

gorithm. There are two types of model. As-

sume that S decision-making processes exist. There-

fore, we consider S decision-making process models

(i|C;β

;x),. ..,P

(i|C;β

;x). These models repre-

sent the probability of service i being chosen from the

universal choice set C under decision-making process

s (s = 1,...,S). Here, x and β

are an explanatory

variable vector and a coefﬁcient vector, respectively.

Suppose that the number of elements in the universal

choice set C is G. That is, there are G combination

of the services in the market. One decision-making

process corresponds to one nested logit (NL) model

(Ben-Akiva and Lerman, 1985; Train, 2003) which

is a type of DCA model. This model can capture

one decision-making process. This is explained in de-

tail in section 3.2. The other model is a class model

π(s;γ;x), where x and γ are the explanatory variable

vector and the coefﬁcient vector, respectively. This

model gives the probability that a customer belongs to

certain decision-making process (class). In this way,

we get the probability of service i being chosen from

universal choice set C as

P(i|C;γ,β;x) =

∑

s=1

π(s;γ;x)P

(i|C;β

;x). (1)

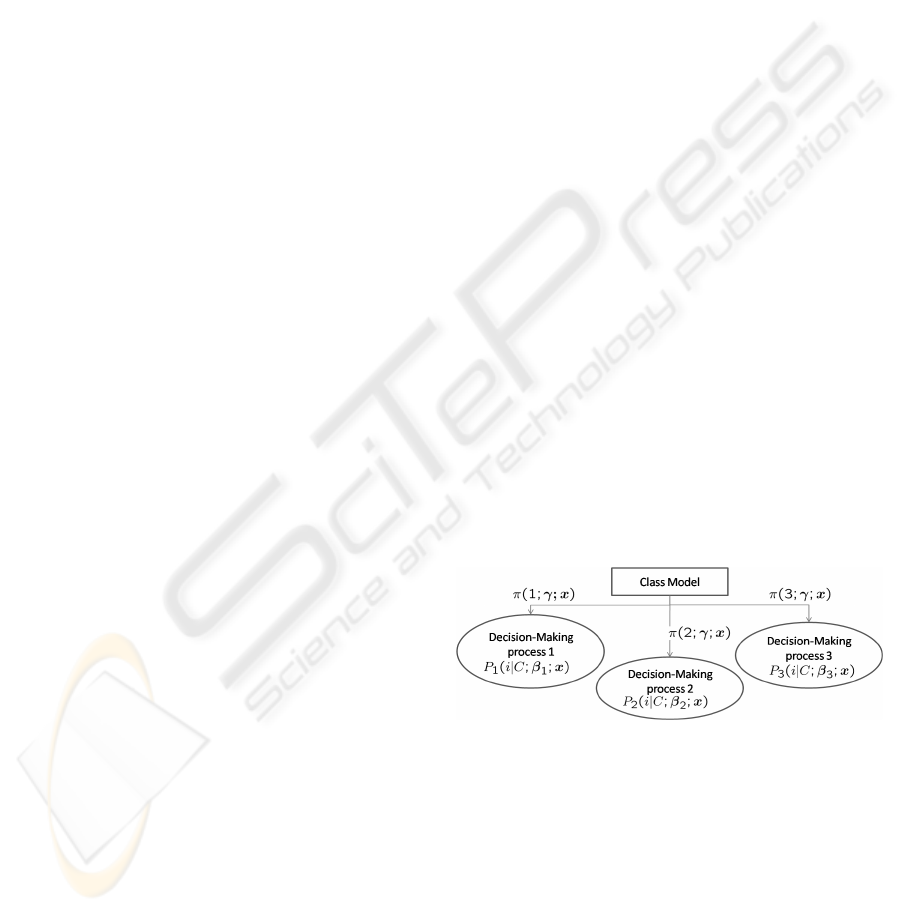
The structure of our model is shown in Fig. 1. This

ﬁgure assumes that there are three types of decision-

making processes.

Figure 1: Choice Model under Various Decision-Making

Processes.

3.1 Class Model

In this section, we deﬁne a class model π(s;γ;x) (0 ≤

π(s;γ;x) ≤ 1 and

∑

s=1

π(s;γ;x) = 1) by using MNL

in DCA (See the appendix A.2). The probability

(s;γ) of customer n using decision-making process

s is given by

(s;γ) = π(s;γ;x

), (2)

ICE-B 2007 - International Conference on e-Business

340

where x

mean attribute values of customer n.

We need the systematic term of utility functions

,.. . ,R

(corresponding to V

in the appendix

A.2). By using these utility functions, we get

(s;γ) =

exp(µR

)

∑

j=1

exp(µR

)

. (3)

Since R

include individual attributes, we can deter-

mine what kind of customers belong to what kind of

decision-making process.

3.2 Decision-Making Process

This section shows how to construct decision-making

process models. We use customer choice results to

construct them. That is, customer n chooses a service

from choice set C

, t (1 ≤ t ≤ T

) times. Then, we

deﬁned these explanatory data as x

(t = 1, ... , T

Here, the probability P

stn

(i|C

;β

) of service i being

chosen by customer n through decision-making pro-

cess s is deﬁned as

stn

(i|C

;β

) = P

(i|C;β

). (4)

To express a decision-making process, we need a hier-

archal structure like a decision tree because a decision

tree can capture the selection order and the correlation

among alternatives. Since this NL model has a hierar-

chical structure representing the decision-making pro-

cess, it is possible to express the model according to

the sequence of selections. Let D

be the depth of the

layered structure. A decision-making structure with a

depth of 2 is shown in Fig. 2 as an example.

Figure 2: Nested logit model (depth=2).

A structure with a depth of 3 is shown in Fig. 3.

The service i is included in a certain alternative

subsets sequence i ∈ C

(1)

stn

⊂ ··· ⊂ C

−1)

−1

stn

⊂ C

The systematic terms of utility function V

(d)

stn

(d)

stn

(1 ≤ k

≤ M

) is deﬁned. For example, as seen

in Fig. 2, when the depth of the decision-making

structure is 2 level hierarchy and the error term is

EV1, the probability of subset C

(1)

stn

being chosen

from all alternative sets C

is given by

stn

(1)

stn

) =

exp(µ

(1)

stn

)

∑

=1,...,M

exp(µ

(1)

stn

)

, (5)

Figure 3: Nested logit model (depth=3).

whereV

(1)

stn

∑

i∈C

(1)

stn

exp(µ

(2)

istn

) (1 ≤ k

≤

). Here, the nesting coefﬁcients µ

and µ

are unknown parameters which are greater than 0.

These nesting coefﬁcients represent the relationship

between a high-level nest and a low-level nest. It is

desirable for the relationship between the nesting co-

efﬁcient and the top nesting coefﬁcient µ

to be like

1 = µ

≤ µ

, (6)

for 1 ≤ k

≤ M

). Generally, it is required that 1 =

≤ µ

≤ ··· ≤ µ

···k

−1

(1 ≤ k

≤ M

,1 ≤ d ≤

− 1). At the second layer, the probability that al-

ternative i is chosen from subset C

(1)

stn

is given by

stn

(i|C

(1)

stn

) =

exp(µ

(2)

istn

)

∑

j∈C

(1)

stn

exp(µ

(2)

jstn

)

. (7)

Therefore, the probability that alternative i is chosen

from all alternative sets C

is expressed as

stn

(i|C

;β

) = P

stn

(i|C

(1)

stn

(1)

stn

), (8)

where β

is an unknown parameter vector that appears

in all utility functions in the decision-making process

s. All nesting coefﬁcients are also contained in un-

known parameter vector β

. Moreover, equation (8) is

generalized to

stn

(i|C

;β

) = P

stn

(i|C

(1)

stn

)

−2

∏

d=1

stn

(d)

stn

(d+1)

d+1

stn

)

stn

−1)

−1

stn

(9)

In this way, we can substitute (8) or (9) into (4).

3.3 Likelihood Function

We can get π

(s;γ) and P

stn

(i|C

;β

) from (3) and (9),

respectively. Therefore, after determining the follow-

ing probability

(i|C

;γ,β) =

∑

s=1

(s;γ)P

stn

(i|C

;β

), (10)

CUSTOMER BEHAVIOR MODELING UNDER SEVERAL DECISION-MAKING PROCESSES BY USING EM

ALGORITHM

341

we can get equation (1) by using (2) and (4). Then,

the maximum likelihood function is deﬁned by

L(γ,β;y, z) =

∏

n=1

∏

s=1

( f

;β

)π

(s;γ))

, (11)

where

;β

) =

∏

t=1

∏

i∈C

stn

(i|C

;β

)

(i)

Here, z

is a dummy variable that takes the value 1

or 0. It is 1 when customer n belongs to a given class

s and 0 when he/she does not. This value is not an

observable variable because we cannot know which

kind of decision-making process a customer will use

to choose a service. Hence, we solve this problem by

using the EM algorithm method. The probability of

belonging to this class (decision-making process) is

given in section 3.4.

3.4 E-Step

Since we do not know what kind of decision-making

process a customer uses when he/she selects a service,

we replace z

by an expectation value obtained using

Bayes’ theory in this E-step (expectation-step). The

posterior probability Q

(s) is deﬁned by

(s) =

(s;γ) f

;β

)

∑

j=1

( j;γ) f

;β

)

. (12)

Namely, π

( j;γ) is given as a prior probability while

(s) is given as a posterior probability. In the ﬁrst

step, since γ and β are unknown parameter vectors,

(s), which is randomly assigned a value between 0

an 1 since it is a probability, is given to every user n.

Hence, by replacing z

by E

] = Q

(s), we get the

likelihood function as

[logL(γ,β;y,z)]

∑

n=1

∑

s=1

(s)log f

;β

)

∑

n=1

∑

s=1

(s)logπ

(s;γ)

∑

s=1

∑

n=1

∑

t=1

(s)log

∏

i∈C

stn

(i|C

;β

)

(i)

∑

n=1

∑

s=1

(s)logπ

(s;γ)

∑

s=1

(β

) +

∗

(γ). (13)

3.5 M-Step

For given log-likelihood function (13), we ﬁnd val-

ues of γ and β that maximize it. From equation (13),

the log-likelihood function is composed of S+ 1 log-

likelihood functions. Since unknown parameters in

γ and β are separated for each log-likelihood func-

tion, we may maximize these S + 1 log-likelihood

functions independently. In this way, we ﬁnd the

maximum solution of the log-likelihood function

[logL(γ,β;y,z)]. Let

β and

γ be the maximum solu-

tions of the log-likelihood function. When we substi-

tuting the obtained

β and

γ into (12), the ﬂow returns

to the E-step. In this way, the E-step and M-step are

executed repeatedly until the log-likelihood function

converges.

4 CASE STUDY

4.1 Menu and Sample

To verify our model, we tested the model with choice

data. We used an online questionnaire system to col-

lect choice data, which were related to the choice

of telephone company. In February 2005, we asked

people which company they would choose and what

kind of optional telephone services they would like

to use The choices included some basic service at-

tributes such as the monthly telephone service charge,

the charge for local calls, and ﬁve optional services

such as a multiple number service. Optional ser-

vice charges were presented for each company, and

optional services could be selected independently of

company choice. Moreover, the choices included two

kinds of discounts (Bundle 1 and 2) for combined op-

tional services. There were four representative com-

panies (Companies A, B, C, and D) and ﬁve optional

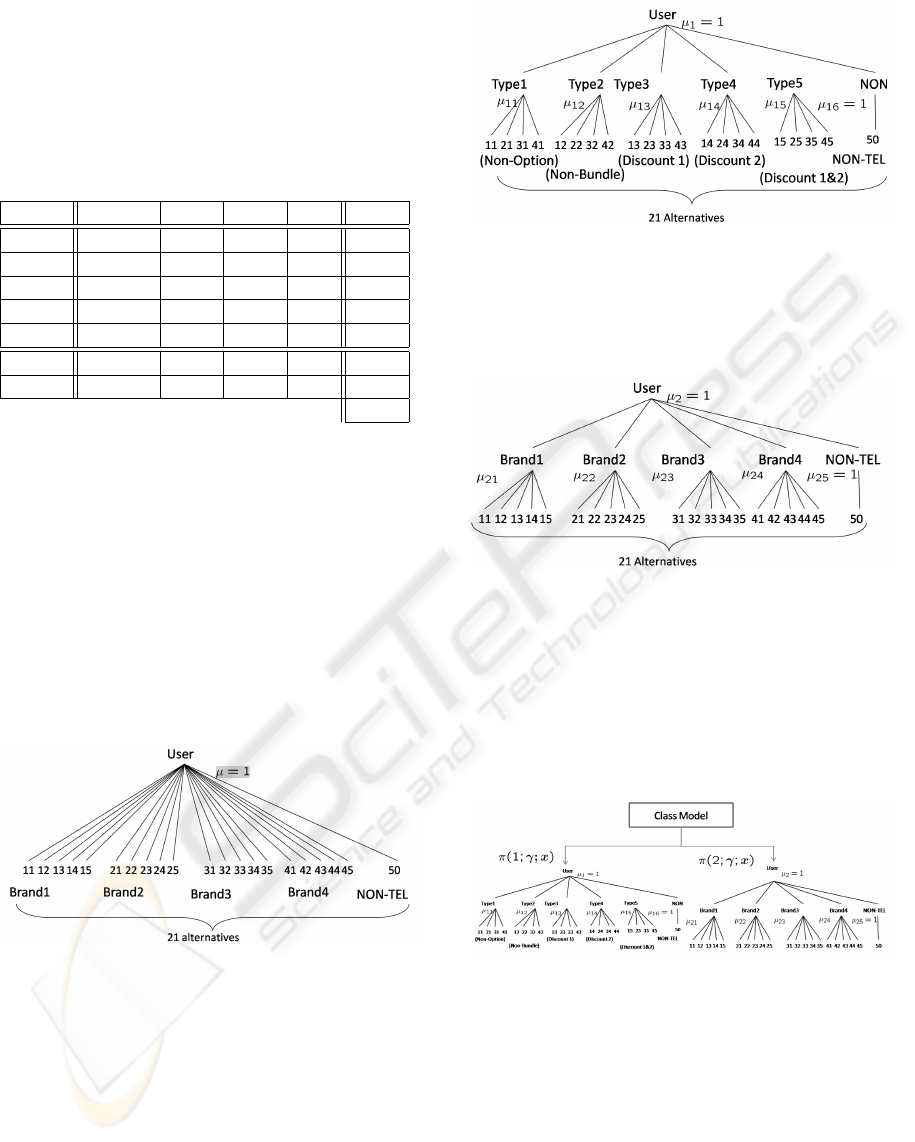
services (OP1, .. . , OP5). We classiﬁed the types of

optional services as follows.

Type 1 No optional services included

Type 2 Non bundling with at least one optional ser-

vice included

Type 3 Bundle 1 discount included

Type 4 Bundle 2 discount included

Type 5 Bundle 1 and 2 discounts included

Thus, there were 4 brands and 5 types of optional ser-

vice. That is, a customer had a choice of 4× 5 + 1 =

21 different alternatives. Here, +1 means not using

any telephone service. This alternative was named 50.

For example, alternative 31 means company C (brand

3) and option type 1 (see Fig. 4). Our questionnaire

ICE-B 2007 - International Conference on e-Business

342

survey received responses from N = 3450 people. Be-

cause they answered the questionnaire 2 or 3 times for

different conditions, we got

∑

n=1

= 7971 observa-

tions. Table 1 shows how many users selected each

brand and option type. ‘None’ means that the cus-

tomer doesn’t select a telephone service.

Table 1: Customer choice distribution.

Brand1 2 3 4 Sum

Type1 666 399 232 122 1419

Type2 1000 592 417 223 2232

Type3 98 60 31 27 216

Type4 1318 748 527 271 2864

Type5 435 253 174 109 971

Sum 3517 2052 1381 752 7702

None - - - - 269

7971

4.2 Implementation

We performed three types of modeling: MNL, NL,

and our EM-algorithm-based model. NL captures a

decision-making process such as a sequence of choos-

ing alternatives and a choice criterion by expressing a

hierarchical structure. In our case study, we simulated

two kinds of NL models. Therefore, we regarded the

total number of models as being 4.

1. MNL model

Figure 4: MNL model.

In the MNL model, the alternatives are at the same

level in the hierarchy. That is, there are 21 alter-

natives at the same level (see Fig. 4).

2. NL model 1: choosing optional services ﬁrst

In this choice model, we assume that a customer

chooses an optional service type at level 1 in Fig.

5. Finally, the customer compares companies. We

call this model NL1. The key feature of this model

is the nodes for the six types.

Figure 5: NL model 1.

3. NL model 2: choosing a company ﬁrst

Figure 6: NL model 2.

In this choice model, we assume that a customer

chooses a company at level 1 and then chooses

the type of optional services at level 2. We call

this model NL2.

4. Model based on the EM algorithm

Figure 7: Model based on the EM algorithm.

This model is based on the EM algorithm. There

are two decision-making processes, that is, this

model includes the two above-mentioned nested

logit models NL1 and NL2.

We used BIOGEME to estimate the MNL, NL1, and

NL2 models. This software is an estimator devel-

oped for DCA models(Bierlaire, 2005). It is splen-

did software for analyzing DCA models. Moreover,

we implemented EM algorithm software to verify our

CUSTOMER BEHAVIOR MODELING UNDER SEVERAL DECISION-MAKING PROCESSES BY USING EM

ALGORITHM

343

model. This EM algorithm software uses BIOGEME

as a core engine for estimation.

4.3 Results

The simulation results for the four models are brieﬂy

presented below. We mainly used adjusted rho

squared

to show the validity of each model (see

the appendix A.2) and nesting coefﬁcients µ.

4.3.1 Results for MNL Model

In the MNL model, we estimated all 21 alternatives

simultaneously. Table 2 shows some of the estima-

tion results obtained with the MNL model. Here,

Table 2: Results for MNL model.

Value t-value Robust t-value

b Bundle1 -42.956 -50.41 -53.51

b Bundle2 -13.403 -51.81 -46.98

b OP1Ch -2.4219 -15.50 -12.63

b OP2Ch -4.6167 -10.45 -9.13

b OP3Ch -5.8008 -15.56 -11.08

b OP4Ch -4.8205 -21.69 -16.95

b OP5Ch -1.6230 -5.51 -4.44

b monthCh -3.5199 -44.31 -38.22

b Bundle1Ch and b Bundle2Ch mean the discount

for bundling optional services. b

OP1Ch and so on

are the charges for optional services, and b

monthCh

is the monthly charge for telephone service. All co-

efﬁcients of explanatory variables have good signs,

where a good sign means, for example, that the utility

goes down in value when the monthly charge goes up.

Moreover, these coefﬁcients have high t-values.

4.3.2 Results for NL Models

NL1 and NL2 obtained good signs, the same as those

in Table 2 for the MNL model. The difference be-

tween the MNL model and the NL models is the nest-

ing coefﬁcient. Tables 3 and 4 show estimated nesting

coefﬁcients.

Table 3: Nesting coefﬁ-

cients of NL1.

Name Value

1.0000

1 (Fix)

Table 4: Nesting coefﬁ-

cients of NL2.

Name Value

6.1707

6.9078

5.9584

6.5349

1 (Fix)

The nesting coefﬁcients of NL1 were estimated

to be 1 in Table 3. By the equation (6), we can see

that µ

= µ

(1 ≤ k

≤ 6). This means NL1 model

does not have the nodes in Fig. 5. That is, the NL1

model is regarded as the MNL model. We can also

see evidence of this in Table 9 because the

NL1 and MNL are nearly equal. On the other hand,

(1 ≤ k

≤ 5) are greater than 1. This means the

NL2 has the nesting structure. NL1 and NL2 have in

inverse relationship, so these results are not strange.

Namely, NL2 is more appropriate than NL1.

4.3.3 Results for Model Based on EM Algorithm

The iteration stopped the maximization after 84 EM-

steps. The model based on the EM algorithm also

obtained good signs, the same as those in Table 2 for

the MNL model. This model includes NL1 and NL2

as two decision-making processes. Tables 5 and 6 are

the nesting coefﬁcients for the EM algorithm model.

Comparing these with the nesting coefﬁcients in Ta-

bles 3 and 5, we ﬁnd that the nesting coefﬁcients of

NL1 in the EM algorithm model (Table 5) have val-

ues exceeding 1. Although these are not always high

values, the EM algorithm model could conﬁrm the ex-

istence of the segment of NL1 type decision-making

process.

Table 5: Nesting coefﬁcient of

NL1 in the EM algorithm.

Name Value

1.3721

1.2128

1.3068

1.0000

1 (Fix)

Table 6: Nesting coefﬁ-

cient of NL2 in the EM

algorithm.

Name Value

7.5094

7.0008

7.0550

6.1438

1 (Fix)

This table 7 shows the class shares. Those class

(decision-making process) shares are obtained from

∑

n=1

(s;

γ)/N for each decision-making process s.

We can see that the share of NL1 is very small. Al-

Table 7: Class share.

NL1 NL2

Class share 7.1% 92.9%

though we could extract NL1, this was not the dom-

inant decision-making process. The reason why µ

of NL1 are close to 1 is derived from same reason.

Those who belong to NL1 class are married female,

live in condominium, and under some conditions. In

addition, the table 8 shows the estimated adjusted rho

ICE-B 2007 - International Conference on e-Business

344

squared ρ

. We can see that ρ

in NL1 (0.4448) is

higher than

(0.6145) in the EM model. This is re-

lated to the results in Table 5. Table 9 summarizes the

Table 8: Adjusted rho squared.

NL model EM model

NL1 0.4448 0.6145

NL2 0.5757 0.5954

results for the four models. It conﬁrms that the EM

model is the most appropriate of these models.

Table 9: Nesting coefﬁcient of NL2 in the EM algorithm.

Model Number of

parameters

Rho-

squared

Adjusted

rho-squared

MNL 26 0.4460 0.4450

NL1 31 0.4460 0.4448

NL2 30 0.5770 0.5757

EM 61 0.5895 0.5870

5 CONCLUSION AND FUTURE

WORK

We tested our model and conﬁrmed that there exist

some decision-making processes. As the result, we

were able to conﬁrm the class NL1 by using EM al-

gorithm. The class model was constructed with the

model including individual variables. Therefore we

could ﬁnd that what kinds of customers are classiﬁed

into certain class. The model is expected to be more

appropriate model when we construct the model with

the larger number of the classes. We think that the ad-

justed rho squared of the model with EM algorithm

did not show much improvement when we assume

there are two decision-making processes, because the

class model could not classify the customers well.

Moreover, the reason why the adjusted rho squared

did not take the higher value is that the number of

customers using an NL1 type decision-making pro-

cess could be small. These are future works. We

would like to consider a more appropriate model by

extracting the dominant decision-making process.

REFERENCES

Ben-Akiva, M. and Gershenfeld, S. (1998). Multi-featured

products and services : analysing pricing and bundling

strategies. Journal of Forecasting, 17:175–196.

Ben-Akiva, M. and Lerman, S. R. (1985). Discrete Choice

Analysis:Theory and Application to Travel Demand.

The MIT Press, Cambridge Massachusetts.

Bierlaire, M. (2005). Biogeme. http://roso.epﬂ.ch/biogeme.

Copeland, T. and Antikarov, V. (2001). Real Options : A

Practitioner’s Guide. Thomson Texere.

Fildes, R. and Kumar, V. (2002). Telecommunications de-

mand forecasting –a review. International Journal of

Forecasting, 18:489–522.

Inoue, A., Nishimatsu, K., and Takahashi, S. (2003a).

Multi-attribute learning mechanism for customer sat-

isfaction assessment. Intelligent Engineering Systems

Through Artiﬁcial Neural Networks, 13:793–800.

Inoue, A., Takahashi, S., Nishimatsu, K., and Kawano,

H. (2003b). Service demand analysis using multi-

attribute learning mechanisms. In KIMAS 2003, pages

634–639, MA Cambridge. IEEE.

Kurosawa, T., Inoue, A., and Nishimatsu, K. (2006). Tele-

phone service choice-behavior modeling using menu

choice data under competitive conditions. Intelligent

Engineering Systems Through Artiﬁcial Neural Net-

works, 16:711–720.

Kurosawa, T., Inoue, A., Nishimatsu, K., Ben-Akiva, M.,

and Bolduc, D. (2005). Customer-choice behavior

modeling with latent perceptual variables. Intelligent

Engineering Systems Through Artiﬁcial Neural Net-

works, 15:419–426.

Loomis, D. G. and Taylor, L. D., editors (1999). THE FU-

TURE OF THE TELECOMMUNICATIONS INDUS-

TRY : Forecasting and Demand Analysis. Kruwer

Academic publishers.

Loomis, D. G. and Taylor, L. D., editors (2001). FORE-

CASTING THE INTERNET : Understanding the Ex-

plosive Growth of Data Communications. Kruwer

Academic publishers.

Manski, C. F. (1977). The structure of random utility mod-

els. Theroy and Decision, 8:229–254.

Nishimatsu, K., Inoue, A., and Kurosawa, T. (2004). Trafﬁc

proﬁling method for service demand analysis. Intelli-

gent Engineering Systems Through Artiﬁcial Neural

Networks, 14:647–652.

Nishimatsu, K., Inoue, A., and Kurosawa, T. (2006).

Service-demand-forecasting method using multiple

data sources. In Networks.

Nishimatsu, K., Inoue, A., Kurosawa, T., Ben-Akiva, M.,

and Bolduc, D. (2005). Service demand analysis : Im-

proved forecasting using model updating. Intelligent

Engineering Systems Through Artiﬁcial Neural Net-

works, 15:691–698.

Savage, S. J. and Waldman, D. (2004). United States de-

mand for internet access. Review of Network Eco-

nomics, 3(3).

Takahashi, S., Inoue, A., Kawano, H., and Nishimatsu, K.

(2004). Scenario simulation based on stated prefer-

ence model. In Simulation Workshop, pages 199–205.

Operational Research Society.

CUSTOMER BEHAVIOR MODELING UNDER SEVERAL DECISION-MAKING PROCESSES BY USING EM

ALGORITHM

345

Train, K. E. (2003). Discrete Choice Methods with Simula-

tion. Cambridge University Press, Cambridge, Mas-

sachusetts.

van der Heijden, K. (1996). SCENARIOS – The Art of

Strategic Conversation. John Wiley & Sons.

A APPENDIX

A.1 Scenario Simulation

Scenario Simulation is a technique for analyzing the

structure of a market. It is a macro model whereas

customer choice behavior modeling is a micro model.

The feature of Scenario Simulation is that it captures

changes in the market by using scenarios. Here, a

scenario means a predetermined future behavior of

the market. By combining some future scenarios,

we can identify the trend of a market depending on

changes to other services, changes in customer tastes,

and changes in customer circumstances. This tech-

nique is similar to the scenario planning approach

(van der Heijden, 1996) or the real options approach

(Copeland and Antikarov, 2001). Its objective is to

analyze service demand by simulating scenarios for

an assumed market structure. The market structure

is divided into a customer behavior layer, a service

layer, and an environment layer. A customer chooses

a service from many alternatives by considering his

or her preferences, the available services, and his/her

circumstances. Each layer requires its own modeling.

The ﬂow of Scenario Simulation is described below.

These steps simulate service demand or trafﬁc vol-

ume by scenarios. A more appropriate simulation is

created by considering the changes in some factors.

1. Deﬁnition : In the ﬁrst step, the conditions related

to the three layers are deﬁned based on predeter-

mined scenarios and collected data.

2. Model construction : In the second step, models

are constructed based on the conditions of each

layer. This step is customer choice behavior mod-

eling.

3. Aggregation : Simulation evaluations are carried

out according to predetermined scenarios. That

is, this step estimates demand by aggregating cus-

tomer choice behaviors.

4. Updating : The scenario is updated based on

changes in each layer.

A.2 Discrete Choice Analysis (DCA)

This section gives an overview of DCA. In DCA, each

alternative has a utility function. The RUM (random

utility maximization) (Manski, 1977) model assumes

that a customer chooses the alternative that has the

highest utility. Let U

be a utility function of alter-

native i of customer n. These explanatory variables

are individual attributes, service attributes, and envi-

ronmental attributes. The utility function U

consists

of a systematic term V

and error term ε

. A cus-

tomer choice set C

, which is a subset of universal

choice set C differs from person to person. A univer-

sal set means a set of all alternatives. Generally, cus-

tomer decision-making processes are complex. That

is, the decision-making process has a multidimen-

sional structure. The structure is expressed like a de-

cision tree (Fig. 2 and Fig. 3).

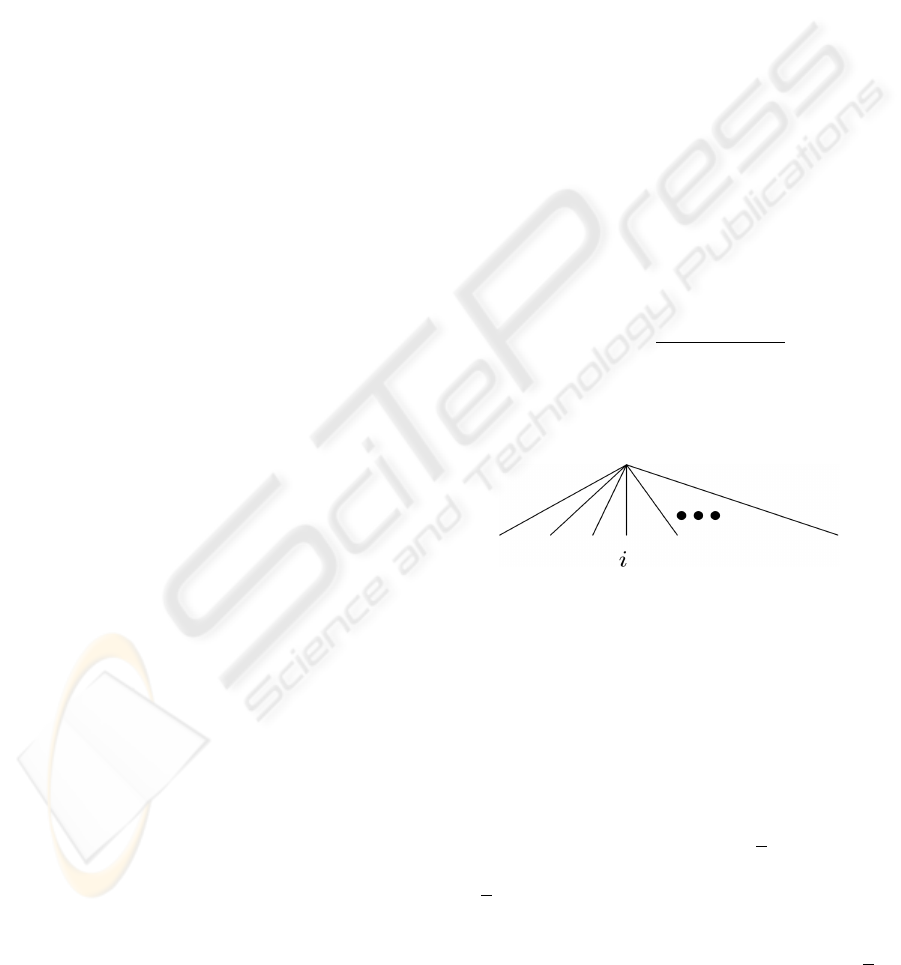
The most popular and simplest model of DCA is

the MNL (multinomial logit) model. This model as-

sumes that alternatives are on the same level in a hi-

erarchy. That is, customer n compares all the alterna-

tives contained inC

, and chooses one alternative (see

Fig. 8). In the case of a simple multinomial choice

problem, if we take extreme value type I (EV1) as a

random error term ε

, then the probability P

(i|C

;β)

of alternative i being chosen is expressed by

(i|C

;β) =

exp(µV

)

∑

k∈C

exp(µV

)

, (14)

where µ is a scale parameter in EV1 that is usually

normalized by 1 and β is an unknown parameter vec-

tor that appears in V

(k ∈ C

). Then, we determine

Figure 8: Multinomial logit model.

the value of β by using maximum likelihood estima-

tion. This function is deﬁned by

L(β;y) =

∏

n=1

∏

i∈C

(i|C

;β)

where N is the number of samples and y

is a dummy

variable that is 1 when a customer n chooses alterna-

tive i and 0 otherwise. Let vector

β be the estimated

vector value of β. In the DCA model,

which shows

the goodness of an index is often used. This is deﬁned

= 1−(L(

β)−K)/L(0), where L(β) = logL(β)

and K is the number of variables. The value lies be-

tween 0 and 1. The model becomes better model if

the value is higher. Generally, the model is good if

takes the value 0.3 or so although this value depends

on the data.

ICE-B 2007 - International Conference on e-Business

346