CLOCK CONTROL SEQUENCE RECONSTRUCTION IN THE

GENERALIZED SHRINKING GENERATOR

Slobodan Petrovi

NISlab, Department of Computer Science and Media Technology, Gjøvik University College, P.O. box 191, 2802 Gjøvik, Norway

Keywords:

Cryptanalysis, Shrinking generator, Edit distance, Correlation attack.

Abstract:

An algorithm is presented that reconstructs the clock control sequence in the generalized shrinking generator

in the presence of noise. The shrinking generator is ﬁrst reduced to a step 1/step E generator, where E depends

on the maximum length of runs of zeros in the output sequence of its clocking part. Then a directed depth-

ﬁrst like search for optimal and suboptimal paths in the edit distance matrix corresponding to the generator

is performed. The permitted path weight deviation from the optimum is determined by the noise level in the

statistical model of the generator. Since the algorithm is deterministic, the correct clock control sequence

is guaranteed to be found, unlike many known algorithms of this kind. Experimental results show that the

algorithm converges to the correct solution relatively fast even if the noise level is high.

1 INTRODUCTION

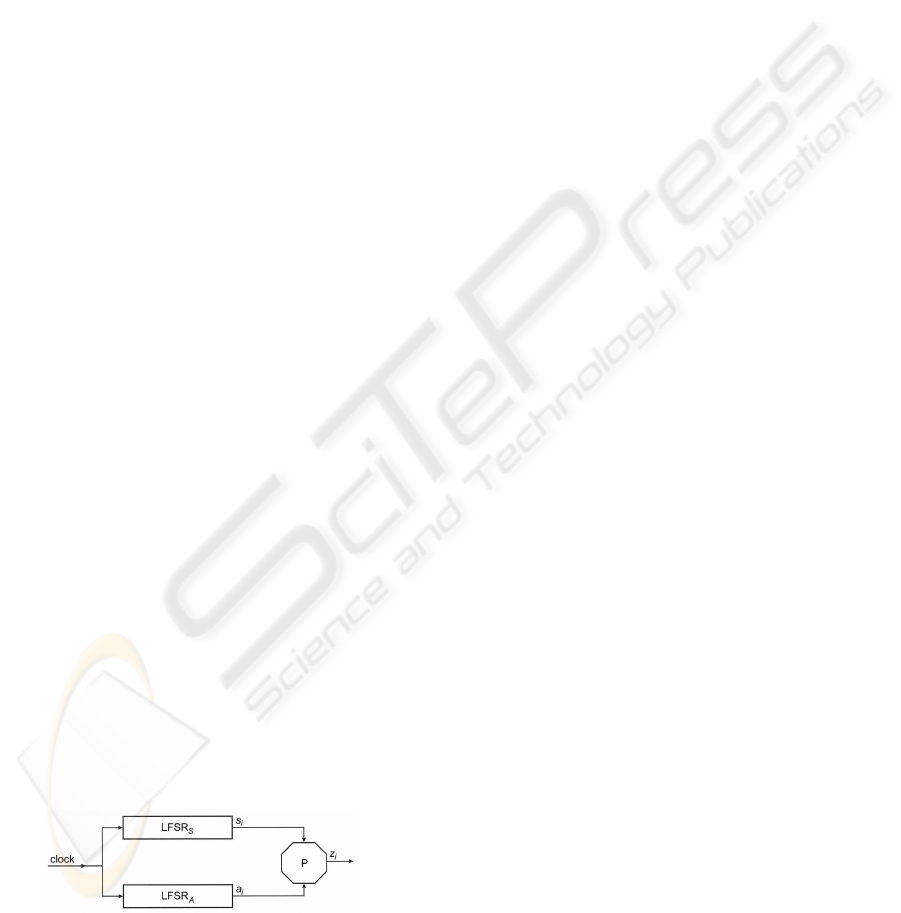
The shrinking generator (Coppersmith et al., 1994) is

a well known pseudorandom sequence generator with

irregular clocking that consists of two linear feedback

shift registers, LFSR

and LFSR

(Fig. 1). If the out-

put sequence from LFSR

is a = a

, a

, . . ., and the

output sequence from LFSR

is s = s

, s

, . . ., then the

output sequence z = z

, z

, . . . of the shrinking gen-

erator is the sequence obtained from a by removing

all a

’s for which s

= 0. The basic scheme of the

shrinking generator can obviously be generalized in

that LFSR

and LFSR

can be replaced by general

type subgenerators.

In (Goli

c and Mihaljevi

c, 1991), it was shown

for a general type pseudorandom generator with ir-

regular clocking that, by making use of a statistical

model employing constrained edit distance, it is pos-

sible to determine a set of candidate initial states of

the clocked LFSR (in this case LFSR

) which could

generate the intercepted output sequence.

Figure 1: The shrinking generator.

Once the set of candidate initial states is known,

the attack continues by determining the clock control

sequence that, together with one of the candidate ini-

tial states of the clocked LFSR, could generate the in-

tercepted sequence.

In this paper, we develop a deterministic method

of reconstruction of clock control sequence in the

generalized shrinking generator for the ciphertext

only attack scenario. Such a generator is ﬁrst re-

duced to a step 1/step E generator, where E depends

on the maximum length of runs of zeros in the output

sequence of its clocking part. Then a ”depth-ﬁrst”-

like search through the constrained edit distance ma-

trix associated with every candidate initial state of the

LFSR

is used. The paths in this matrix that corre-

spond to the candidate clock control sequences are re-

constructed. Inﬂuence of noise is taken into account

by relating the noise level with the permitted weight

deviation from the optimum path weight used in the

search process. By starting with the reconstruction

of paths whose weight deviation from the optimum is

0 (the optimal paths - without noise) and then by in-

creasing this weight deviation according to the noise

level (the suboptimal paths), we make our search a

directed one.

2 REDUCTION TO THE STEP

1/STEP E GENERATOR

Consider the shrinking generator from the Fig. 1, with

LFSR

eventually replaced with a general type sub-

generator. In the rest of the article we call this block

the clocking part of the generator. Each run of zeros

259

Petrovi

c S. (2007).

CLOCK CONTROL SEQUENCE RECONSTRUCTION IN THE GENERALIZED SHRINKING GENERATOR.

In Proceedings of the Second International Conference on Security and Cryptography, pages 259-262

DOI: 10.5220/0002118402590262

 SciTePress

in the output sequence s of the clocking part of the

generator produces a run of deletions in the output se-

quence a of the LFSR

. The maximum length of runs

of deletions is equal to the maximum length E of runs

of zeros in the sequence s. Thus, instead of the shrink-

ing generator from Fig. 1, it is possible to analyze the

equivalent step 1/step E generator presented in Fig. 2.

Figure 2: The step 1/step E generator equivalent to the gen-

eralized shrinking generator.

In the reconstruction of the clock control sequence

in the generalized shrinking generator, it is possible to

use the statistical model of the step 1/step E generator

(Fig. 3). The register R in this model corresponds to

the LFSR

from the Figs. 1 and 2, without decima-

tion.

Figure 3: The statistical model of the step 1/step E genera-

tor.

Let {x

} be the binary sequence produced by the

shift register R. Let {d

} be a sequence of integers,

named decimation sequence, 0 ≤ d

≤ E, where E

is given in advance. In the decimation process, the

sequence {z

} is obtained in the following way:

= x

f(n)

, f(n) = n+

∑

i=0

, n = 0, 1, 2, . . . (1)

The correlation attack described in (Goli

c and Mi-

haljevi

c, 1991) is based on the edit distance measure

with the constraint on the maximum length of runs

of deletions. This edit distance can be determined in

an iterative way, by ﬁlling the matrix of partial con-

strained edit distances. For the rest of the paper, we

use the term edit distance matrix, for simplicity. In

the edit transformation, if e represents the number of

deletions and s represents the number of substitutions,

then the edit distance between the preﬁx X

e+s

of the

sequence X and the preﬁx Y

of the sequence Y is

given by the following expression:

W[e, s] = min{W[e− e

, s− 1] + e

+ d(x

e+s

, y

) |

max{0, e−min{N−M, (s−1)E}} ≤ e

≤ min{e, E}}

s = 1, . . . , M e = 1, . . . , min{N − M, sE}, (2)

where d

represents the elementary edit distance as-

sociated with a deletion (we assume that this value is

constant), d(x, y) represents the elementary edit dis-

tance associated with the substitution of the symbol

x by the symbol y and E is the maximum number of

consecutive deletions. From now on, we assume that

d(x, y) = 0 iff x = y. The constrained edit distance

between X and Y is obtained at W[N − M, M].

In the ﬁrst phase of the attack (see (Goli

c and Mi-

haljevi

c, 1991)), the length N of the output sequence

of the LFSR R without decimation is estimated. In or-

der to reduce additional noise generated by estimation

of N, we use the mathematical expectation of N cal-

culated on the basis of the mathematical expectation

of E. It is also necessary to determine the threshold T

needed for the classiﬁcation of the initial states of R.

This is done by using the probability of ”false alarm”

as well as the probability of ”missing the event”

, which are selected in advance. For every pos-

sible initial state of R, the constrained edit distance

between its corresponding output sequence of length

N and the intercepted sequence of length M is com-

puted. All the initial states that produce the output

sequences from R, whose edit distance from the inter-

cepted output sequence is less than the threshold T,

are included in the set of candidate initial states.

3 CLOCK CONTROL SEQUENCE

RECONSTRUCTION

We call the optimal paths the paths through the edit

distance matrix that begin at W[N − M, M]. Let pl ≤

M be the length of the clock control sequence needed

to reconstruct the initial state of the subgenerator

mentioned above. The optimal paths pass through

the cells W[e

, pl], . . . ,W[e

, pl] in the column pl

of the matrix W, where n depends on the particular

sequences.

To determine the points in the column pl, through

which the optimal paths pass, every cell W[e, s] has,

besides the value c of the edit distance, four associated

vectors:

1. The vector of ’primary’ pointers

vp to the cells W[vp[1], s − 1], . . . ,

W[vp[k], s − 1] from which it is possible to

arrive to the cellW[e, s] with the minimum weight

increment, k ≤ E + 2.

2. The vector of ’updated’ point-

ers vu to the cells W[vu[1], pl], . . . ,

W[vu[l], pl], through which it is possible to

arrive to the cellW[e, s] with the minimum weight

increment, l ≤ min{N − M + 1, E(1+ pl)}.

SECRYPT 2007 - International Conference on Security and Cryptography

260

3. The vector of pointers ve to the cells W[ve[1], s −

1], . . . , W[ve[ j], s− 1] from which it is possible to

arrive to the cell W[e, s] regardless of the weight

increment, j ≤ E +2.

4. The vector of values v j of the edit distances cor-

responding to the elements of the vector ve. The

cardinality of this vector is also j.

The actual values of k, l, and j depend on the par-

ticular sequences. The matrix W is ﬁlled by means of

the algorithm, which implements the equation (2) to-

gether with the updating of the four vectors mentioned

above. The complete algorithm is given below:

Algorithm 1

Input:

• The sequences X and Y of lengths N and M, re-

spectively.

• The necessary length pl of the optimal/suboptimal

path to be reconstructed.

• The maximum length E of runs of deletions (note

that we use the mathematical expectation of E).

• The elementary distance d

associated with the

deletion of a symbol.

• The elementary edit distance d[x, y] associated

with the substitution of the symbol x with the sym-

bol y, ∀(x, y).

Output:

• The array W of edit distances with the vectors vp,

vu, vj, and ve associated with every cell.

comment Initialization

max

←− min{N, M} ;

max

←− max{min{N − s, s∗ E}}, s = 1, . . . , s

max

;

W[e, s].c ←− ∞ , e = 0, . . . , e

max

, s = 0, . . . , s

max

; the

vectors vp, vu, v j, and ve associated with every cell

W[e, s] are empty.

W[0, 0].c ←− 0 ;

comment Main loop

for s ←− 1 until s

max

begin

for e ←− 1 until min{N − s, s∗ E} do

begin

Let q be the minimum value of the expression

W[e− e

, s− 1].c+ e

∗ d

+ d[X[e+ s],Y[s]],

= max{0, e− min{N − s, (s− 1) ∗E}}, . . . ,

min{e, E}, (3)

Let n

be the number of values of e

for which the

expression (3) takes the value q. Then

W[e, s].c ←− q ; W[e, s].k ←− n

;

W[e, s].vp is ﬁlled with n

values of the expression

(e− e

) corresponding to the values e

for which

the expression (3) takes the value q. W[e, s].vj

is ﬁlled with all the values of the expression (3).

W[e, s].ve is ﬁlled with the values (e − e

) corre-

sponding to the values of W[e, s].v j.

end ;

comment Determining updated pointers vu.

if s = pl + 1 then

W[e, s].vu ←− W[e, s].vp,

e = 0, . . . , min{N − s, s∗ E} ;

else if s > pl + 1 then

For every element of W[e, s].vp, e =

0, . . . , min{N − s, s ∗ F}, the elements of

W[W[e, s].vp[i], s − 1].vu, i = 1, . . . ,W[e, s].k

are placed into W[e, s].vu, deleting the repeated

ones.

end.

From now on, by paths we mean fragments of

paths that start in the column pl of the matrix W.

There are three sets of paths to be reconstructed. The

ﬁrst one consists of optimal paths that start at the

points e

= W[N − M, M].vu[i], i = 1, . . . ,W[e, s].l.

The second one consists of suboptimal paths, whose

weight-difference from the optimal ones is ≤

D ,

a threshold given in advance that depends on the

noise level, that start at e

= W[N − M, M].vu[i], i =

1, . . . ,W[e, s].l. The third set consists of suboptimal

paths, whose weight-difference from the optimal ones

is ≤

D , that start at other points in the column pl.

The coordinates of the vector W[N − M, M].vu at

the end of the execution of the Algorithm 1 repre-

sent the initial points of the search for the elements

of the ﬁrst and second set mentioned above. As

for the third set, if | W[e

, pl].c − W[e, pl].c |≤

D ,

e = 0, . . . , min{N − M, sE}, e 6= e

, for at least one i,

then the point W[e, pl] is an initial point of the search

for the paths of the third set.

In order to determine the optimal and suboptimal

paths that start at every initial point

E of any set, a

special depth-ﬁrst like search algorithm was devised.

In this algorithm, every branching point is processed

by enumerating systematically all the paths that start

in it. In this search, a special kind of stack is used.

A reconstructed path is rejected if at some point its

weight becomes greater than the optimal weight plus

D . The complete algorithm is given below:

Algorithm 2:

Input:

• The array W of edit distances, obtained by means

of the Algorithm 1.

• The values of pl,

E and D .

Output:

CLOCK CONTROL SEQUENCE RECONSTRUCTION IN THE GENERALIZED SHRINKING GENERATOR

261

• All the paths that start at the point W[E , pl] that

belong to the corresponding set(s) (see text).

repeat

Starting from the cell W[E , pl], reconstruct in the

depth-ﬁrst manner all the paths, whose weight-

differences from the optimal paths are ≤

D . On

each examined path, the cells of the array W to be

processed after the current cell W[e, s] are deter-

mined by the pointer vector W[e, s].ve (see Algo-

rithm 1).

until all the paths have been examined.

4 EXPERIMENTAL RESULTS

The number of paths necessary to ﬁnd the clock con-

trol sequence increases with

D . Because of that, given

certain level of noise in the statistical model of the

generator, the behaviour of the maximum value of D ,

denoted by

max

, was analysed experimentally.

The experiment was carried out in the following

way: 1000 initial states of the shrinking generator

were chosen at random. For each of them, the out-

put sequence corrupted by the random noise sequence

was produced. The noise level p (i.e. the probability

of 1 in the noise sequence) was the control variable of

the experiment. The set of candidates for the initial

state of LFSR

was determined. Once the candidates

were obtained, for a ﬁxed value of

D , the optimal

and suboptimal paths were determined from the edit

distance matrix corresponding to each of them. This

process was repeated starting from

D = 0 and incre-

menting the value of

D until the correct clock control

sequence generated by LFSR

was found. The maxi-

mum value D

max

obtained in this process was stored.

At the end of the experiment, the mean value

max

over the values of

max

obtained in every case was

computed. The dependence of

max

on p for two dif-

ferent values of pl is depicted in the Fig. 4.

It can be observed from the Fig. 4 that even for

high levels of noise, the obtained values of

max

were

relatively small for the chosen values of pl, which

means relatively fast convergence of the clock control

sequence reconstruction algorithm.

5 CONCLUSION

In this paper, a deterministic method of clock control

sequence reconstruction in the shrinking generator in

the presence of noise is described. The inﬂuence of

noise is taken into account by relating the noise level

with the permitted deviation from the noiseless-case

Figure 4: Dependence of D

max

on p.

path weight in the clock control sequence reconstruc-

tion process. The shrinking generator is ﬁrst reduced

to a general step 1 / step E generator, where E is the

maximum length of runs of zeros in the clock control

sequence. Then, the statistical model of the step 1 /

step E generator that employs the constrained edit dis-

tance is used to obtain the edit distance matrix associ-

ated with every candidate initial state of the LFSR

The clock control reconstruction is performed by a di-

rected depth-ﬁrst like search through the edit distance

matrix. The search starts with the reconstruction of

the paths with zero deviation from the noiseless case

path weight and then this deviation is iteratively in-

cremented. The maximum value of weight deviation

necessary for the reconstruction of the actual clock

control sequence depends on the noise level. Exper-

imental results show that the average deviation from

the noiseless case increases moderately with the noise

level, which means that the clock control sequence

reconstruction procedure converges relatively rapidly

even for higher levels of noise.

REFERENCES

Coppersmith, D., Krawczyk, H., and Mansour, Y. (1994).

The shrinking generator. In Procceings of Crypto 93,

Lecture Notes in Computer Science 773, pages 22–39.

Springer-Verlag.

Goli

c, J. and Mihaljevi

c, M. (1991). A generalized cor-

relation attack on a class of stream ciphers based

on the levenshtein distance. Journal of Cryptology,

3(3):201–212.

SECRYPT 2007 - International Conference on Security and Cryptography

262