IMPROVING SECURITY IN CHAOTIC SPREAD SPECTRUM
COMMUNICATION SYSTEMS WITH A NOVEL ‘BIT POWER
PARAMETER SPECTRUM’ MEASURE
Branislav Jovic
Department of Electrical and Computer Engineering, University of Auckland, 38 Princes street, Auckland, New Zealand
Charles Unsworth
Department of Engineering Science, Univesity of Auckland, 70 Symonds street, Auckland, New Zealand
Keywords: Security, Spread Spectrum, Communications, Chaos, PC Synchronization, Bit Power Parameter Spectrum.
Abstract: Due to the broadband nature and the high sensitivity to parameter and initial conditions in chaotic signals,
chaotic spread spectrum (SS) communication systems have been regarded as highly secure. However, it is
often easier to decrypt chaotic parameter modulation (CPM) based SS systems than was originally thought.
In this paper, a single user CPM based chaotic communication system implementing Pecora-Carroll (PC)
synchronization is described. Following this, the CPM based communication system, employing the chaotic
carrier generated by the Burger’s map is proposed. To highlight the security aspect a new measure called
‘Bit Power Parameter Spectrum’ (BPPS) is introduced. The BPPS is then used to identify parameters that
provide high secure and insecure regions for the chaotic map. Furthermore, it is demonstrated how a binary
message can be decrypted easily if the parameters of the map exist in the insecure region of the BPPS and
how security is optimised if the parameters exist in the secure region of the BPPS. The results are contrasted
with those of the standard Lorenz CPM based system. The BPPS measure shows that the Lorenz CPM
based system is easily decrypted for nearly all parameter values thus rendering the carrier insecure.
1 INTRODUCTION
In 1990 Pecora and Carroll (PC) discovered that
chaotic systems can be synchronized. Along with the
broadband nature and the high sensitivity of chaotic
systems to parameter and initial condition
perturbations, chaotic synchronization allowed
researchers to design SS chaotic communication
systems. These systems were primarily designed
with the aim of the increased security over the
existing SS systems. However, as will be discussed
shortly, chaotic communications are often insecure.
A PC synchronization scheme can be viewed as
a master-slave synchronization system (Jovic et al.,
2006a). The master system provides at least one of
its chaotic outputs to the slave system. The slave
system uses the given master output (driving signal),
to elegantly synchronize itself to the master system,
regardless of its initial conditions. The master-slave
system can also be viewed as the transmitter-
receiver communication system. Since the
introduction of the PC synchronization method a
number of communication schemes based on this
method have been proposed, (Wu and Chua, 1994;
Oppenheim et al., 1992; Cuomo and Oppenheim,
1993; Jovic et al., 2006a). These include such
methods as the chaotic masking (CS) (Oppenheim et
al., 1992), the chaotic parameter modulation (CPM)
(Cuomo and Oppenheim, 1993) and the initial
condition modulation (ICM) (Jovic et al., 2006a).
Other chaotic SS communication systems, such as
those based on DS-CDMA synchronization also
exist and have been studied in (Jovic et al. 2007a).
In contrast to PC synchronization where the
master-slave system either synchronizes or does not,
it is also possible to design controllers which enforce
synchronization. Such design techniques have been
investigated for both chaotic flows (Jovic and
Unsworth, 2007b) and chaotic maps (Millerioux and
Mira, 1998, 2001; Yan, 2005). In a number of cases
it has been shown that these techniques can be
273
Jovic B. and Unsworth C. (2007).
IMPROVING SECURITY IN CHAOTIC SPREAD SPECTRUM COMMUNICATION SYSTEMS WITH A NOVEL ‘BIT POWER PARAMETER SPECTRUM’
MEASURE.
In Proceedings of the Second International Conference on Security and Cryptography, pages 273-280
DOI: 10.5220/0002125302730280
Copyright
c
 SciTePress

applied to chaotic communications (Millerioux,
1998; Nan, 2000). In (Millerioux and Mira, 1998,
2001) synchronization of piecewise linear chaotic
maps in a master-slave configuration is investigated.
In particular, finite time synchronization is
considered and the conditions for it discussed. It is
shown that finite time synchronization requires the
eigenvalues of the error system matrix to be equal to
zero. The significance of the results in relation to
secure chaotic communications is also discussed.
A similar method to that of the master-slave map
synchronization of (Millerioux and Mira, 2001) is
proposed here. In our method the general approach
to master-slave synchronization of chaotic maps is
presented and the requirements for synchronization
outlined. It is shown that the synchronization is
achieved by keeping the eigenvalues of the error
system matrix within the unit circle in the z domain.
Furthermore, the method of implementing the
synchronized master-slave system within a CPM
based secure SS chaotic system is demonstrated.
With the development of secure communication
techniques based on the concept of chaotic
synchronization, eavesdropping techniques have also
been developed in parallel, highlighting the lack of
security in many of the proposed systems. The
eavesdropping techniques include those based on the
prediction attacks (Short, 1994), short-time zero-
crossing rate (STZCR) attacks (Yang, 1995),
generalized synchronization attacks (
Álvarez et al.,
2004c), return map attacks (Pérez and Cerdeira,
1995), spectral analysis attacks (
Álvarez et al.,
2004b), and parameter estimation attacks (Álvarez et
al., 2004a), among other.
In perhaps the broadest of terms the chaotic
communication eavesdropping techniques, in the
literature today, can be divided into those which
directly extract the transmitted message without the
knowledge of the dynamics of the transmitter (Short,
1994; Yang, 1995;
Álvarez et al., 2004b), and those
which make certain assumptions about the dynamics
of the transmitter before attempting the extraction of
the message (
Álvarez et al., 2004a, 2004c).
In this paper, it is demonstrated how one can
decrypt a binary message from a CPM based SS
communication system with no prior knowledge of
the dynamics of the transmitter. The message
extraction technique is based on the average power
of the received signal which for a secure system
must be equal for both bits 0 and 1. The carrier
powers of bits 0 and 1 must be equal, or very nearly
equal, to each other to eliminate the possibility of
recognising the message from these (
Álvarez et al.,
2004c). It is shown that in terms of the bit power
security, the Burgers’ map CPM system can be
optimized and outperforms the Lorenz CPM system.
2 SS CHAOTIC
SYNCHRONIZATION BASED
COMMUNICATION SYSTEMS
In this section, the chaotic communication system
with the receiver based on the PC chaotic
synchronization, namely chaotic parameter
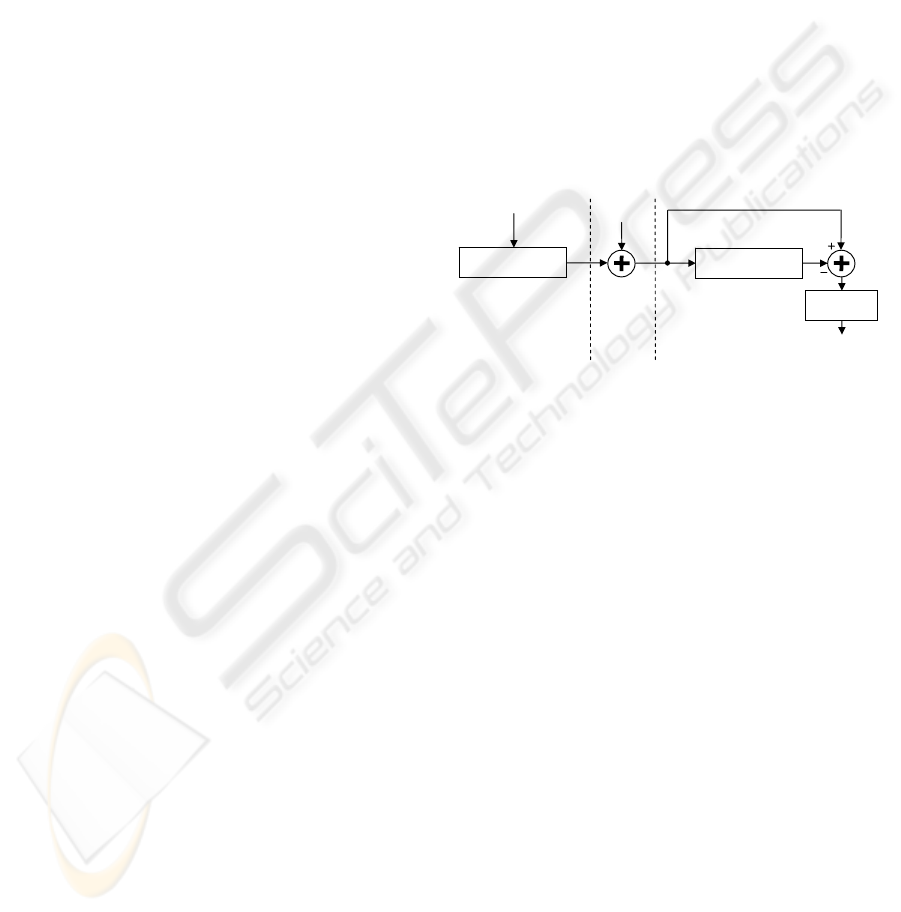
modulation (CPM) is briefly described.
A block
diagram of a SS chaotic communication system
based on the CPM concept is shown in Figure 1. A
requirement for the CPM scheme is for the master-
slave system to synchronize for a given driving
signal (Jovic and Unsworth, 2007b).
Slave system
n
Transmitter Channel Receiver
∧
m
∧
x
r
x
x
Master system
m
Detector
Figure 1: A block diagram of the chaotic communication
system based on the parameter modulation concept.
In Figure 1, the message signal m varies between
the two particular values, depending on whether a
binary 0 or a binary 1 is to be transmitted. The
message is incorporated into a certain modulating
parameter of the master system causing it to change
its value with the change in the message. The
parameters of the slave system are fixed at all time.
When the master-slave parameters are identical
synchronization occurs. This forces the
synchronization error to zero, indicating that bit 0
has been transmitted. Alternatively, with the master-
slave parameter mismatch the system does not
synchronize, indicating that bit 1 has been
transmitted. Assuming that the additive white
Gaussian noise (AWGN) component n is near zero,
and that sufficient amount of time has passed for
r
x
and
∧
x
to synchronize, the transmitted message m is
recovered in the form of
∧
m
. The choice of the
modulating parameter of the master chaotic system
must be chosen with care to ensure chaotic
properties of the system at all time. This ensures the
increased security within the communication system.
SECRYPT 2007 - International Conference on Security and Cryptography
274

3 GENERAL APPROACH TO
THE DESIGN OF THE
SS CHAOTIC
SYNCHRONIZATION BASED
COMMUNICATION SYSTEMS
In this section, the general approach to the design of
the synchronized chaotic maps is proposed and
applied to the design of the CPM based SS
communication systems.
3.1 Synchronization of Chaotic Maps
In (Pecora and Carroll, 1990), the chaotic
synchronization concept with a single signal of the
master system supplied to the slave system is
considered. The general result of this is that the
master-slave system either synchronizes or does not
(Pecora and Carroll, 1990; Jovic et al, 2006a). In this
subsection, the design of nonlinear controllers for
the chaotic map master-slave systems is proposed. In
particular, the method is demonstrated on the two
dimensional Burgers’ chaotic map. These controllers
then ensure the synchronization among the master-
slave systems. The design of the nonlinear control
laws is via the following theorem:
Theorem 1:
Suppose:
nnnnn
eUeAe +=
+1
,
∀
0≥n
,
1)()( <=+ BeigUAeig
nn
.
Then:
0→
n
e
, as
∞→n
,
∀
n
Re ∈
0
.
The theorem states that the equilibrium 0, of the
error system
1+n
e , is globally asymptotically stable
if and only if all eigenvalues of
nn
UAB +=
have
magnitude less than one.
Special case: If the matrix B is a function of n,
then the condition that
nn
BB −
+1
remains
bounded must also be satisfied.
In the above theorem the brackets | | denote the
magnitude of the eigenvalues of a matrix, and the
brackets || || denote the Euclidian norm. In the
following sections theorem 1 is used for the purpose
of synchronizing one, two and three dimensional
master-slave chaotic maps.
3.2 SS Communication System based
on the Synchronization of Burgers’
Map Master-Slave Chaotic System
In this subsection, the master-slave synchronization
of the Burgers’ map master-slave system is
considered and the CPM based SS communication
system proposed.
The Burgers’ map (Whitehead and MacDonald,
1984) is given by equation 1:
nnnn
nnn
YXbYY
YaXX
+=
−=
+
+
1
2
1
(1)
With the parameters a = 0.75 and b = 1.75 the
system is chaotic.
The design procedure of the synchronizing
nonlinear control laws of the Burgers’ map CPM
based SS chaotic communication system of Figure 2
is now explained. Let the error be defined by
equation 2:
n
n
n
XXe −=
∧
1
(2a)
n
n
n
YYe −=
∧
2
(2b)
In order to demonstrate the design of the controller
of Figure 2 assume no noise in the system. It follows
then that:
nnr
YY
=
. The difference error, (the error
system), can then be represented by equation 3:
n
nn
nn
n
n
n
n
n
n
n
n
n
n
n
n
n
uYXYXbYYb
YYe
uYYaXXa
XXe
2
1
1
1
2
1
2
2
1
1
1
1
+−+−=
−=
++−−=
−=
∧∧∧
+
+
∧
+
∧∧
+
+
∧
+
(3)
Equation 3 can also be represented by equation 5,
keeping in mind the identities of equation 4:
n
n
n
nnn
nn
n
n
n
n
n
n
eXeYYXYX
eYeYYY
21
22
2
2
∧∧∧
∧∧
+=−
−−=+−
(4)
n
n
nn
n
n
n
n
n
nnn
uXbeeYe
uYYeaee
221
1
2
121
1
1
)(
)(
+++=
+−−+=
∧
+
∧
+
(5)
With theorem 1 in mind matrix equation 6 is
formed:
nnnnn
eUeAe +
=
+1
(6)
IMPROVING SECURITY IN CHAOTIC SPREAD SPECTRUM COMMUNICATION SYSTEMS WITH A NOVEL
‘BIT POWER PARAMETER SPECTRUM’ MEASURE
275

Transmitter
(Master system)
nnnn
n
nn
YXbYY
Y
XmaX
+=
−
+
=
+
+
1
2
1
)19.0(
0
Y
0
0
YY ≠
∧
Receiver
(Slave system)
n
nnnn
n
nnn
uYXYbY
uYXaX
2
1
1
2
1
++=
+−=
∧∧∧
+
∧
∧∧
+
∧
n
m
n
Y
nr
Y
n
Y
∧
∫
dt
2
)(
∧
m
0
X
0
0
XX ≠
∧
nyn
ee =
2
Controller:
n
n
n
n
nr
n
n
eXbu
eYYu
22
21
)(
)(
∧
∧
+−=
+=
n
u
2
n
u
1
Figure 2: The Burgers’ map SS chaotic communication system based on the parameter modulation concept.
where:
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
n
n
n
nn
nn
n
nn
nn
n
e
e
e
uu
uu
U
aa
aa
A
2
1
2221
1211
2221
1211
,,
.
Therefore:
n
nn
nn
n
nn
nn
n
e
uu
uu
e
aa
aa
e
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
=
+
2221
1211
2221
1211
1
(7)
Modifying equation 5 to fit the matrix form of
equation 7, equation 8 is obtained:
n
n
n
nn
n
n
n
n
n
n
e
uu
uu
e
XbY
YYa
e
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−−
=
∧
∧
+
iviii
iii
1
(8)
where:
nnnnn
eueuu
2ii1i1
+=
,
n
n
nnn
eueuu
2iv1iii2
+=
.
Therefore:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+++
+−−+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−−
=+=
∧
∧
∧
∧
n
n
n
n
n
n
n
n
n
n
nn
n
n
n
n
nn
uXbuY
uYYua
uu
uu
XbY
YYa
UAB
iviii
iii
iviii
iii
(9)
Following theorem 1 the control laws can be
chosen in the following manner:
)(,0,,0
iviiiiii
n
n
n
n
n
nn
XbuuYYuu
∧∧
+−==+==
(10)
With the control laws of equation 10, the matrix
B of equation 9 takes the form of equation 11:
⎥
⎦
⎤
⎢
⎣
⎡
=
0
0
n
n
Y
a
B
(11)
It is then readily verifiable that the eigenvalues
of matrix
n
B of equation 11 are equal to 0 and a.
Furthermore, the theorem 1 above requires matrix
B
to be constant. As the matrix
B is a function of n, it
must also be ensured that
nn
BB −
+1
remains
bounded to guarantee global asymptotic stability
which is the requirement for synchronization. The
fact that
nn
BB −
+1
remains bounded is
demonstrated by equation 12:
0
0
0
0
0
0
0
0
0
1
)1(
)1(
→
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
+
−+
+
−++
n
i
i
n
in
in
nninin
Ya
a
Y
a
Y
a
Y
a
eBBB KK
∀
|a| < 1, and as ∞→i . (12)
Therefore, as stated in equation 12, in order for
the master and slave systems of Figure 2 to
synchronize, the parameter
a must be kept within the
unit circle in z domain.
The control laws
n
u
1
and
n
u
2
are therefore
given by equations 13 and 14, and incorporated into
Figure 2.
SECRYPT 2007 - International Conference on Security and Cryptography
276

n
n
n
nnnnn
eYYeueuu
22ii1i1
)( +=+=
∧
(13)
n
n
n
n
nnn
eXbeueuu
22iv1iii2
)(
∧
+−=+=
(14)
The important feature of the master-slave system of
Figure 2 is that it only requires the master signal
n
Y
to synchronize the master and slave systems. This
fact is of particular importance for communications
as only one signal needs to be transmitted thus
reducing the required bandwidth (Jovic et al.,
2006a,b).
In Figure 2, the master system parameter set of
015.0=a
and
75.1=b
has been chosen to represent
a bit 0. The master system parameter set of
205.0
=
a
and
75.1=b
has been chosen to represent a bit 1.
The reasoning behind such choice of parameters is
clarified in the next section. Note that the message
m
of Figure 2 takes on the values of 0 and 1 depending
on the polarity of a bit transmitted. The slave system
parameters are set for all time at
015.0=a
and
75.1=b
, so that synchronization at the receiver side
signals a bit 0 and de-synchronization signals a bit 1.
Both parameter sets,
015.0
=
a
and
75.1=b
, and
205.0=a
and
75.1=b
generate chaotic behaviour
within the system (Whitehead and MacDonald,
1984).
The transmitted signal
n
Y is shown in Figure 3
when the series of 10 bits is transmitted, that is,
when
m = [0 0 1 0 1 1 0 1 0 1]. Figure 3 also shows
the corresponding squared synchronization error,
2
ny
e
, under noiseless conditions.
0 500 1000 1500 2000 2500 3000 3500 4000
-1.5
-1
-0.5
0
0.5
1
1.5
Yn
Transmitted signal
n
0 500 1000 1500 2000 2500 3000 3500 4000
0
0.01
0.02
0.03
0.04
0.05
0.06
ey
2
n
n
Error squared
Transient
Bit 1
Bit 0
10
Figure 3: The transmitted signal
n
Y
and the squared
synchronization error
2
ny
e
.
The received bits are detected by squaring and
integrating the error
ny
e
. The output of the integrator
is then compared to the predetermined threshold and
the decision is made whether a bit 0 or a bit 1 was
sent. Note that the spreading factor of 400 has been
used to represent one bit. By definition, the
spreading factor denotes the number of discrete
points (chips) contained within one information bit.
It is the ratio of a bit period to a chip period (Jovic
and Unsworth, 2007b). A transient period of 10
chips has been allowed for the case of Figure 3.
During the transient period there is no data
transmission taking place.
4 BIT POWER SECURITY
ISSUES OF THE SS CHAOTIC
COMMUNICATION SYSTEMS
In this section, highly secure and insecure regions of
the Burgers’ map CPM based SS communication
system are identified using a new measure called the
‘Bit Power Parameter Spectrum’ (BPPS). The
analysis is also performed on a standard Lorenz
CPM based SS system. It is shown that an
eavesdropper can readily decode the message,
without any assumptions about the system, if the
system is operated outside the secure regions of the
BPPS.
4.1 Security Evaluation of the Burgers’
Map CPM based SS Chaotic
Communication System
For any secure chaotic communication system it is
imperative that the power of the chaotic carriers
representing bits 0 and 1 be approximately equal to
avoid the possibility of decoding information by a
third party simply based on the average powers of
the chaotic carriers (Álvarez et al., 2004c). In order
to perform the security analysis on the Burger’s map
communication system of Figure 2, and thus explain
the choice of the modulating parameters, the average
power of the chaotic carriers representing bits 0 and
1 is now analysed. To do so the average power of a
number of bits (1024) is first calculated and the
mean of those powers and the corresponding
standard deviation found. A number of points are
then obtained for a number of different sets of
chaotic parameters and the average power graph,
with the error bars, versus the varied parameter,
plotted. A pseudo random binary sequence (PRBS)
generator has been used to model the transmitted
bits. The plots have been produced with the concept
of security in mind. If the average power of the
IMPROVING SECURITY IN CHAOTIC SPREAD SPECTRUM COMMUNICATION SYSTEMS WITH A NOVEL
‘BIT POWER PARAMETER SPECTRUM’ MEASURE
277

chaotic carriers of bits 0 and 1 are different during
the same transmission, with the confidence intervals
which do not overlap, then the security of the system
based on those carriers is jeopardized.
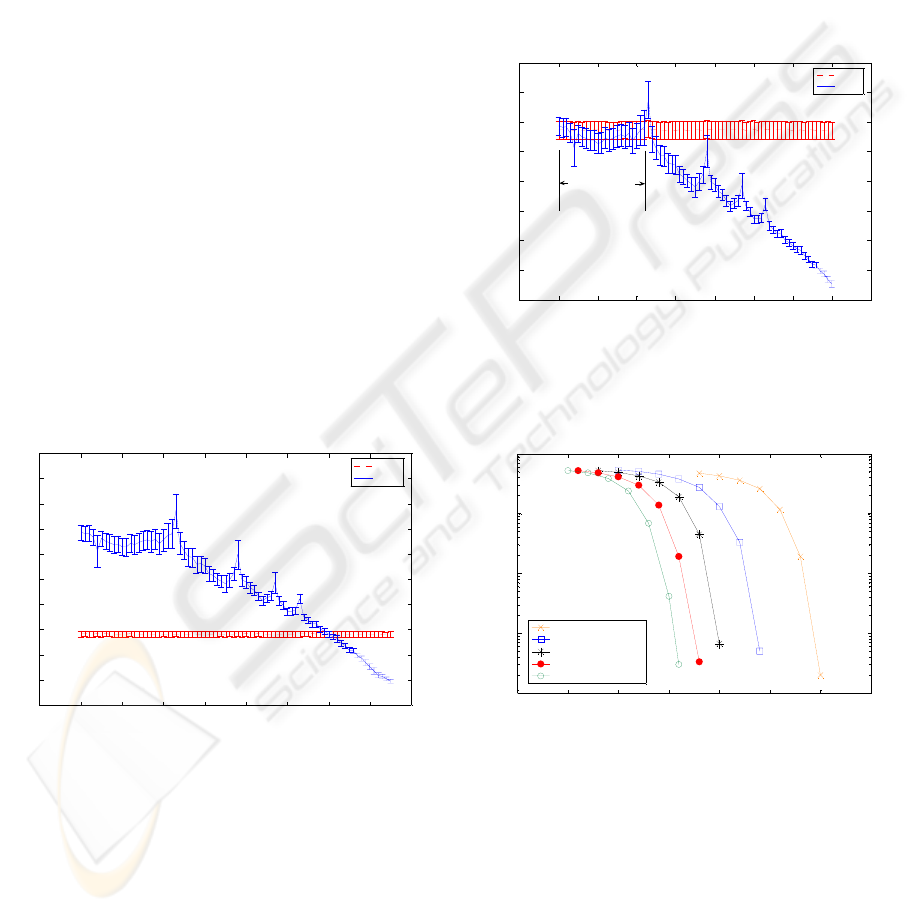
Figure 4 shows the BPPS of the chaotic carriers
representing the bits transmitted. For the bits 1 the
parameter
b is always kept constant at 1.75 with the
parameter a varied in steps of 0.01 from a = 0 to a =
0.75. For the case of Figure 4 bits 0 are represented
by the parameter values:
a = 0.6 and b = 1.75 at all
times. Bits 1 must then be represented by some other
parameter values in order to achieve successful
communication. From Figure 4 it can be observed
that the average power of the chaotic carriers is
approximately the same, (and the deviation of this
power), when the parameter
a is kept in the region: 0
< a < 0.22, whereas it differs drastically outside of
this region. Therefore, choosing the parameter sets
for bits 0 and 1 anywhere outside this region would
jeopardize the security of the system. Thus,
choosing the parameter values:
a = 0.6 and b = 1.75
to represent bits 0 is not suitable for the security
reasons. In order to remedy this let the parameter
values representing bits 0 be:
a = 0.015 and b = 1.75.
In this case Figure 5 is obtained. From Figure 5 it is
observed that the carrier powers of the bits 0 and 1
have approximately equal values thus offering
increased security over the choice of parameters of
Figure 4.
-0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
Bit powe
r
Parameter a representing bits 1
Bits 0
Bits 1
Figure 4: The BPPS within the Burgers’ CPM based SS
chaotic communication system when the bits 0 are
represented by the parameter set: a = 0.6, b = 1.75.
Based on the findings of Figure 5, it is now
shown that choosing the parameter set: a = 0.015
and b = 1.75, to represent bits 0, and the parameter
set,
a = 0.205 and b = 1.75, to represent bits 1,
produces the best performance in terms of the bit
error rate (BER). In Figure 6, the BER vs. the bit
energy to noise power spectral density ratio (E
b/No)
curves have been plotted. Figure 6 demonstrates the
progressive improvement represented by the BER
curves with the parameter
a varied in the secure
region of Figure 5 from
a = 0.0625 up to a = 0.205
in steps of 0.0475. The parameter b has been set to
1.75 for both bits 0 and 1. The parameter a
representing bit 0 has been set to:
a = 0.015. Note
that the best BER performance is achieved by
choosing the parameter sets, representing bits 0 and
1, to be as far apart as possible from each other
within the secure region of Figure 5. Also note
further improvement in the BER curve, marked by
the open circles, as one exits the secure region.
-0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
Bit power
Parameter a representing bits 1
Bits 0
Bits 1
Secure region
Figure 5: The BPPS within the Burgers’ CPM based SS
chaotic communication system when the bits 0 are
represented by the parameter set: a = 0.015, b = 1.75.
30 35 40 45 50 55 60 65
10
-4
10
-3
10
-2
10
-1
10
0
BER
Eb/No (dB)
Bits 1 par. a = 0.0625
Bits 1 par. a = 0.11
Bits 1 par. a = 0.1575
Bits 1 par. a = 0.205
Bits 1 par. a = 0.26
Figure 6: The secure region BER curves of the SS chaotic
communication system based on the parameter modulation
of the Burgers’ chaotic map with the progressively
increasing bits 1 parameter a.
Figure 7 illustrates the effect on security caused by
choosing inappropriate parameter sets which
produce chaotic carriers of different power. In case
of Figure 7 bits 0 have been represented by the
parameter set of
a = 0.6 and b = 1.75, while bits 1
have been represented by the parameter set of
a =
0.205 and b = 1.75. The average power of the
SECRYPT 2007 - International Conference on Security and Cryptography
278

transmitted signal of Figure 7 has been evaluated
using the sliding window of 400 chips in length (the
spreading factor of a single bit). The sliding
window is then shifted one chip in time and the
average power evaluated again. This process is
repeated until the end of the transmitted signal. It
can be observed from Figure 7 that the average
power of the chaotic carriers of the transmitted bits
oscillates periodically with the change of the binary
message. In contrast to Figure 7, Figure 8 illustrates
the effect on security caused by choosing the
appropriate parameter sets which produce chaotic
carriers of approximately equal power. In case of
Figure 8 bits 0 have been represented by the
parameter set of
a = 0.015 and b = 1.75, while bits 1
have been represented by the parameter set of a =
0.205 and b = 1.75.
0 500 1000 1500 2000 2500 3000 3500 4000
-0.5
0
0.5
1
1.5
Bits
Binary message
0 500 1000 1500 2000 2500 3000 3500 4000
-2
0
2
Yn
Transmitted signal
0 500 1000 1500 2000 2500 3000 3500 4000
0.2
0.3
0.4
0.5
Power
Time
Average Power
Figure 7: The binary message, the transmitted signal
n
Y
and the average power of the transmitted signal. Bits 0
parameter set: a = 0.6 and b = 1.75. Bits 1 parameter set:
a = 0.205 and b = 1.75.
0 500 1000 1500 2000 2500 3000 3500 4000
-0.5
0
0.5
1
1.5
Bits
Binary message
0 500 1000 1500 2000 2500 3000 3500 4000
-2
0
2
Yn
Transmitted signal
0 500 1000 1500 2000 2500 3000 3500 4000
0.2
0.3
0.4
0.5
Power
Time
Average Power
Figure 8: The binary message, the transmitted signal
n
Y
and the average power of the transmitted signal. Bits 0
parameter set: a = 0.015 and b = 1.75. Bits 1 parameter
set: a = 0.205 and b = 1.75.
4.2 Security Evaluation of the Lorenz
CPM based SS Chaotic
Communication System
In (Cuomo and Oppenheim, 1993), the Lorenz CPM
based SS chaotic communication system has been
presented. In this scheme the binary message is used
to alter the parameter
b of the master (transmitter)
between 4 and 4.4 depending on whether a bit 0 or
bit 1 is to be transmitted. However, at the slave
(receiver) side the parameter
b is fixed at 4 for all
time. Thus, the synchronization either occurs or does
not, depending on the state of the parameter
b at the
transmitter (master) side. The other Lorenz
parameters, namely
σ and r, are fixed at 16 and 45.6,
respectively. A BPPS as that of Figures 4 and 5 is
plotted in Figure 9 but for the Lorenz CPM based
chaotic communication system of (Cuomo and
Oppenheim, 1993). In this case the parameter
b of
the bits 1 is varied from 0.1 to 10 in steps of 0.1 with
the other parameters being fixed at the constant
values specified above. From Figure 9 one can see
that there are no secure regions where one can
operate the system as the power of the bits 1
increases, almost linearly, with the parameter
b.
Therefore, to minimise the impact on the security,
the parameters
b representing bits 0 and 1, must be
kept as close to each other as possible.
0 2 4 6 8 10
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
Bit power
Parameter b representing bits 1
Bits 0 power
Bits 1 power
Figure 9: The BPPS within the Lorenz CPM based SS
chaotic communication system. The close up is shown in
the upper left hand corner.
5 CONCLUSIONS
In this paper, a method of synchronizing chaotic
maps and its implementation within a CPM based
SS chaotic communication system has been
proposed. The security of the proposed, as well as of
the existing SS chaotic communication systems, has
3 3.5 4 4.5 5
1.2
1.4
1.6
1.8
IMPROVING SECURITY IN CHAOTIC SPREAD SPECTRUM COMMUNICATION SYSTEMS WITH A NOVEL
‘BIT POWER PARAMETER SPECTRUM’ MEASURE
279

then been evaluated in terms of the average power of
the chaotic carriers of the bits transmitted. In order
to do so, a novel analysis technique, termed the ‘Bit
Power Parameter Spectrum’ (BPPS), has been
proposed. Without any assumptions about the
system architecture or its characteristics, the BPPS
has been used to show that the CPM based SS
systems are not as secure as often thought.
The design of the nonlinear control laws for the
synchronization of the chaotic map master-slave
systems has been proposed and demonstrated on the
two dimensional Burgers’ map master-slave system.
Following this, the method of implementing the
synchronized master-slave system within a CPM
based secure SS communication system has been
demonstrated on the two dimensional Burgers’ map.
The nonlinear control laws were designed in such a
way to force the synchronization among the master
and slave systems using only one signal of the
master system. This is of particular importance for
communications as only one signal needs to be
transmitted thus reducing the required bandwidth.
Finally, the Lorenz CPM based SS chaotic
communication system has been presented. The
security of the proposed and the existing CPM SS
chaotic communication systems has been evaluated
in terms of the average power of the chaotic carriers
of the bits transmitted using the newly proposed
technique of BPPS. It has then been shown that due
to the largest BPPS overlap region, the Burgers’ map
CPM based SS chaotic communication system can
be optimized and is thus more secure than the
Lorenz CPM based SS system. As the BPPS relies
on the evaluation of average power, the security
optimization is thus achieved by assuming that an
eavesdropper has no knowledge of the system
architecture or its dynamics. Furthermore, it has
been shown that the BER performance of the
Burgers’ map CPM based SS chaotic
communication system can also be optimized. The
optimization is achieved by choosing the parameter
sets, representing bits 0 and 1, to be as far apart as
possible within the secure operating region of the
BPPS.
REFERENCES
Álvarez, G., Montoya, F., Pastor, G., Romera, M., 2004a.
Breaking a secure communication scheme based on
the phase synchronization of chaotic systems. Chaos,
14 (2), 274-278.
Álvarez, G., Montoya, F., Romera, M., Pastor, G., 2004b.
Breaking Two Secure Communication Systems Based
on Chaotic Masking. IEEE Trans. Circuits Systems:
Express Briefs, 51 (10), 505-506.
Álvarez, G., Montoya, F., Romera, M., Pastor, G., 2004c.
Breaking parameter modulated chaotic secure
communication system. Chaos, Solit. Fract., 21 (4),
783-787.
Cuomo, K.M., Oppenheim, A.V., 1993. Circuit
Implementation of Synchronized Chaos with
Applications to Communications. Phys. Rev. Lett., 71
(1), 65-68.
Jovic, B., Berber, S., Unsworth, C.P., 2006a. A novel
mathematical analysis for predicting master – slave
synchronization for the simplest quadratic chaotic flow
and Ueda chaotic system with application to
communications, Physica D, 213 (1), 31-50.
Jovic, B., Unsworth, C.P., Berber S., 2006b. De-noising
‘Initial Condition Modulation’ Wideband Chaotic
Communication Systems with Linear & Wavelet
Filters. In AUS Wireless‘06, 1st IEEE Internat. Conf.
on Wireless Broadband and Ultra Wideband
Communications.
Jovic, B., Unsworth, C.P., Sandhu, G.S., Berber, S.M.,
2007a. A robust sequence synchronization unit for
multi-user DS-CDMA chaos-based communication
systems, Signal Processing, 87 (7), 1692-1708.
Jovic, B., Unsworth, C.P., 2007b. Synchronization of
Chaotic Communication Systems. In C.W. Wang
(Ed.), Nonlinear Phenomena Research Perspectives,
Nova Publishers, New York, In Press.
Millerioux, G., Mira, C., 1998. Communicating via Chaos
Synchronization Generated by Noninvertible Maps. In
ISCAS’98,Internat. Symp. Circuits and Systems.
Millerioux, G., Mira, C., 2001. Finite-Time Global Chaos
Synchronization for Piecewise Linear Maps, IEEE
Trans. Circuits Systems, 48 (1), 111-116.
Nan, M., Wong, C-n., Tsang, K-f., Shi, X., 2000. Secure
digital communication based on linearly synchronized
chaotic maps, Phys. Lett. A, 268 (1-2), 61-68.
Oppenheim, A.V., Wornell, G.W., Isabelle, S.H., Cuomo,
K.M., 1992. Signal processing in the context of
chaotic signals. In Proc. IEEE ICASSP’92.
Pecora, L.M., Carroll, T.L., 1990. Synchronization in
chaotic systems, Phys. Rev. Lett., 64 (8), 821-824.
Pérez, G., Cerdeira, H.A., 1995. Extracting Messages
Masked by Chaos, Phys. Rev. Lett, 74 (11), 1970-1973.
Short, K.M., 1994. Steps Toward Unmasking Secure
Communications, Internat. J. Bifur. Chaos, 4 (4), 959-
977.
Whitehead, R.R., MacDonald, N., 1984. A chaotic
mapping that displays its own homoclinic structure,
Physica D, 13 (3), 401-407.
Wu, C.W., Chua, L.O., 1994. A unified framework for
synchronization and control of dynamical systems,
Internat. J. Bifur. Chaos, 4 (4), 979-998.
Yan, Z., 2005. Q-S synchronization in 3D Henon-like map
and generalized Henon map via a scalar controller,
Phys. Lett. A, 342 (4), 309-317.
Yang, T., 1995. Recovery of Digital Signals from Chaotic
Switching, Internat. J. Circuit Theory Applic., 23 (6),
611-615.
SECRYPT 2007 - International Conference on Security and Cryptography
280