SUBQUADRATIC BINARY FIELD MULTIPLIER IN DOUBLE

POLYNOMIAL SYSTEM

Pascal Giorgi

, Christophe Nègre

Équipe DALI, LP2A, Unversité de Perpignan

avenue P. Alduy, F66860 Perpignan, France

Thomas Plantard

Centre for Computer and Information Security Research

School of Computer Science & Software Engineering

University of Wollongong, Australia

Keywords:

Binary Field Multiplication, Subquadratic Complexity, Double Polynomial System, Lagrange Representation,

FFT, Montgomery reduction.

Abstract:

We propose a new space efﬁcient operator to multiply elements lying in a binary ﬁeld F

. Our approach is

based on a novel system of representation called Double Polynomial System which set elements as a bivariate

polynomials over F

. Thanks to this system of representation, we are able to use a Lagrange representation

of the polynomials and then get a logarithmic time multiplier with a space complexity of O(k

1.31

) improving

previous best known method.

1 INTRODUCTION

Efﬁcient hardware implementation of ﬁnite ﬁeld

arithmetic, and speciﬁcally of binary ﬁeld F

, is

often required in cryptography and in coding the-

ory (Berlekamp, 1982). For example in elliptic curve

cryptosystem (Koblitz, 1987; Miller, 1986), the main

operation is the scalar multiplication on the curve,

which necessitates thousands of multiplications and

additions over a ﬁnite ﬁeld. Similarly, hundreds of

multiplications over a binary ﬁeld are required for

the Difﬁe-Hellman Key exchange protocol (Difﬁe and

Hellman, 1976).

Previously to this work, several architectures have

already been proposed to efﬁciently implement the

arithmetic in F

. These architectures are mostly ded-

icated to the multiplication since this operation is ex-

tensively used and is often the most expensive. Each

of them takes advantage of a special representation of

the ﬁeld. In particular, one of them uses polynomial

basis or shifted polynomial basis (Mastrovito, 1991;

Fan and Dai, 2005) while another uses normal ba-

sis (Gao, 1993; Hasan et al., 1993). The latter pro-

viding a really efﬁcient squaring in the ﬁeld since in

this basis the squaring is just a cyclic shift of the co-

efﬁcients.

In these representations the main approach to per-

form the multiplication consists to express the oper-

ation as a matrix-vector product with binary entries.

Parallel architectures are thus capable to perform this

product within logarithmic time. However, these ar-

chitectures still achieve a space complexity of k

. Ac-

cording to the recent improvements proposed in (Fan

and Hasan, 2007), one can still perform the matrix-

vector product in logarithmic time but with a space

complexity of k

1.56

or k

1.63

. This has been made pos-

sible thanks to structured matrices such as Toeplitz

ones and a divide-and-conquer approach for the prod-

ucts.

In this paper we propose a new approach which

reduces the exponent in the space complexity to 1.31

while keeping a logarithmic time complexity. First,

we introduce a novel system of representation, the

Double Polynomial System. In this representation,

elements of F

are polynomials in two variables

A(t,Y) =

∑

n−1

i=0

(t)Y

where a

(t) have degree strictly

less than r.

Therefore, as in classical polynomial represen-

tation, the multiplication can be performed in two

steps: a polynomial multiplication, and then a reduc-

tion phase to reduce the degrees in Y and in t.

The reduction in Y is simple due to the deﬁnition

of DPS. The same is not true for the reduction in t.

Here, we use a Montgomery-like reduction approach

in order to perform this reduction with few polyno-

mial multiplications, this enabling us to easily use

229

Giorgi P., Nègre C. and Plantard T. (2007).

SUBQUADRATIC BINARY FIELD MULTIPLIER IN DOUBLE POLYNOMIAL SYSTEM.

In Proceedings of the Second International Conference on Security and Cryptography, pages 229-236

DOI: 10.5220/0002126102290236

 SciTePress

the Fast Fourier Transform. Therefore, our multiplier

fully beneﬁts from the FFT process which is highly

parallelizable and provides a subquadratic space com-

plexity.

Hence, we propose a binary ﬁeld multiplier which

has a delay of (16 log

(k) + 20)T

+ 8T

and a space

complexity of O(k

1.31

), where T

and T

correspond

respectively to the delay of one XOR gate and one

AND gate.

Let us brieﬂy give the outline of the paper. We

ﬁrst introduce the DPS representation for binary ﬁelds

(Section 2). We present the DPS multiplication in

Section 3 and discuss the problem of ﬁnding a suit-

able polynomial to achieve our Montgomery-like co-

efﬁcient reduction in Section 4. Then, we present

in Section 5 a modiﬁed version of our multiplica-

tion introducing Lagrange basis. We recall in Sec-

tion 6 some basic facts on the architecture design of a

ternary FFT. We ﬁnally conclude this paper by a de-

tailed explanation of the complete architecture for our

DPS-Lagrange multiplier and its complexity analysis

and comparison (Section 7).

2 DPS REPRESENTATION

A binary ﬁeld F

is generally constructed as the set

of polynomials modulo an irreducible polynomial P ∈

[t] of degree k

= F

[t]/(P(t))

= {A(t) ∈ F

[t] s.t. degA(t) < k}

We introduce a novel binary ﬁeld representation,

the Double Polynomial System (DPS), inspired from

AMNS number system of Bajard et al. (J.-C. Bajard,

2005).

Deﬁnition 1 (DPS representation). A Double Poly-

nomial System (DPS) is a quintuplet B = (P,γ,n,r,λ)

such that

• P(t) ∈F

[t] is an irreducible polynomial of degree

• γ(t),λ(t) ∈ F

[t]/(P(t)) satisfy

γ(t)

≡ λ(t) mod P,

and λ(t) has a low degree in t.

A DPS representation of an element A(t) ∈ F

[t]/(P)

is a polynomial A

(t,Y ) ∈ F

[t,Y ] such that

(t,Y ) =

n−1

∑

i=0

(t)Y

with deg

(t) < r

and A

(t,γ(t)) ≡A(t) mod P

In the sequel we will often omit the subscript B to

denote the DPS form of an element A. In some cases,

when it is clear from the context, we may discard the

variables t,Y to deﬁne the DPS representation of an

element. We will also denote by E the polynomial

E = Y

−λ.

Example 1. Let us consider the ﬁeld F

, then the

quintuplet B = (P = t

+t + 1,γ = t

t,n = 3,r = 2,λ = t) is a DPS for this ﬁeld. We can

check this with Table 1 which gives the DPS expres-

sion of each element in F

Table 1: Elements of F

in B.

A(t) 0 t

+t + 1 t

0 (t + 1)Y

Y +1 Y

+t + 1

A(t) 1 t

+ 1 t

+t t

+t + 1

1 (t + 1)Y

+ 1 Y Y

A(t) t t

+t t

+ 1

t Y

+Y +1 Y +t Y

A(t) t + 1 t

+t + 1 t

+ 1 t

t + 1 Y

+Y Y + t + 1 Y

+ 1

In particular, we can verify that if we evaluate (t +

1)Y

+ 1 in γ, we get (t + 1)γ

+ 1 = (t + 1)(t

+1 = t

+1 mod P, as expected. One can also see

that deg

((t + 1)Y

+ 1) = 2 < 3 = n and deg

((t +

1)Y

+ 1) = 1 < 2 = r. ♦

Remark 1. The DPS can be seen as a generalization

of the polynomial representation of double extensions

. Such extensions are usually constructed ﬁrst as

= F

[t]/(P(t)) and then as F

= F

[Y ]/(Y

−λ)

with λ ∈ F

, see (Guajardjo and Paar, 1997). How-

ever, this construction is not possible when the degree

k of the ﬁeld F

is prime. DPS provides an alternative

for double extension in this situation.

Remark 2. As in classical polynomial representa-

tion, the addition in DPS is just a parallel bitwise

XOR on the coefﬁcients.

We proceed now by considering the problem of

the multiplication of two elements expressed in a

DPS. This can be done in two steps as described in

Algorithm 1.

The ﬁrst step of the algorithm consists of a clas-

sical polynomial multiplication modulo the binomial

E(Y ) = (Y

−λ). The resulting polynomial C(t,Y)

satisﬁes C(t, γ) = A(t, γ)B(t, γ) mod P(t) since E(γ) ≡

0 mod P(t) by deﬁnition of the DPS.

The second step computes an element R(t,Y) such

that it becomes a valid DPS representation of A ×B:

R(t,γ) = A(t,γ)B(t, γ) mod P(t) and deg

(R) < r.

SECRYPT 2007 - International Conference on Security and Cryptography

230

Algorithm 1: DPS multiplication scheme.

Input : A,B ∈ B = (P,γ,n,r,λ)

Output: C = A×B ∈ B

1. Polynomial multiplication in Y :

C = AB mod (Y

−λ).

2. Coefﬁcients reduction :

R = RedCoe f f (C).

It is clear from the DPS system and from the multi-

plication modulo a binomial Y

−λ that C has coef-

ﬁcients c

(t) with degree in t bounded by 2(r −2) +

deg

λ. Therefore, these coefﬁcients must be reduced

to get the result of the multiplication expressed in the

DPS representation.

3 MULTIPLICATION IN DPS

A straightforward method for the reduction phase in

t of Algorithm 1 is to perform an Euclidean division

C = Q ×M + R where deg

R < r. This reduction is

only valid if M(t,Y ) is monic in t and satisﬁes

M(t,γ) ≡0 mod P(t) with deg

(M) = r. (1)

Generally, one can easily compute a polynomial M

satisfying equation (1), e.g. Section 4, but ensuring

monicity is difﬁcult.

Algorithm 2: DPS Multiplication.

Input : A, B ∈ B = (P,γ,n,r,λ)

with E = Y

−λ

Data : M such that M(γ) ≡ 0 mod P,

a polynomial m ∈ F

[t] and

= −M

−1

mod (E, m)

Output: R such that

R(t,γ) = A(t,γ)B(t, γ)m

−1

mod P

begin

C ← A ×B mod E;

Q ←C ×M

mod (E, m);

R ← (C + Q ×M mod E)/m;

end

In order to avoid monicity attached to a divi-

sion strategy, we adapt the Montgomery trick (Mont-

gomery, 1985) to our DPS system. The idea is to re-

place the Euclidean division by few multiplications

and one exact division. This corresponds to annihi-

lating the lower part of the c

(t) instead of the higher

ones. This method is given in Algorithm 2 assuming

a polynomial M(t,Y ) satisfying M(t, γ) ≡0 mod P(t)

is given.

Example 2. We consider the ﬁeld F

, with the DPS

B = (P = t

+t + 1, γ = t

+t, n = 3,r =

2,λ = t). In Table 2, we give an example of trace of

DPS multiplication.

Table 2: DPS multiplication trace.

Operations Resul ts

A tY

+tY

B (t + 1)Y +t

M tY

+Y + t + 1

(1 + t)Y

+ (1 +t)Y + 1

m t

C tY

Y +t

Q tY

Q ×M (t

+t)Y

Y +t

C + Q ×M t

+ (t

)Y + t

R Y

+ (t + 1)Y +t

We can check that R(t, γ) ≡t

+t mod P is equal

to A(t,γ)B(t, γ)t

−2

mod P. ♦

Lemma 1. Algorithm 2 is correct.

Proof. We need to demonstrate that the output R of

the algorithm satisﬁes the following equation

R(t,γ) = A(t,γ)B(t, γ)m

−1

mod P. (2)

From the deﬁnition 1 of DPS representation, we

know that E(γ) ≡ 0 mod P. Thus, we have

C(t, γ) ≡ A(t,γ)B(t,γ) mod P.

By deﬁnition of M, we have M(t,γ) ≡ 0 mod P and

consequently

C(t, γ) + Q(t, γ)M(t, γ) ≡ C(t, γ)

≡ A(t,γ)B(t, γ) mod P

We now need to prove that the division by m is ex-

act. This is equivalent to prove the following equiva-

lence C + Q ×M mod E ≡ 0 mod m. By deﬁnition,

we have Q = C ×M

mod E and M

= −M

−1

mod

(E,m). We consider R

= C + Q ×M mod (E, m),

then the following equivalences hold

≡ C +C ×(−M

−1

×M) mod (E,m)

≡ (C −C) mod (E,m)

≡ 0 mod (E,m).

Thus, division by m is exact. Hence, the algorithm

is correct since an exact division (the division by m)

is equal to the multiplication by an inverse modulo

SUBQUADRATIC BINARY FIELD MULTIPLIER IN DOUBLE POLYNOMIAL SYSTEM

231

At this level, we know that the resulting polyno-

mial R of the previous algorithm satisﬁes the equation

R(t,γ) = A(t,γ)B(t,γ)m

−1

mod P but we do not know

whether it is expressed in the DPS, i.e., if the coefﬁ-

cients of R have degree in t smaller than r. This is the

goal of the following theorem.

Theorem 1. Let B = (P,γ,n,r,λ) a Double Poly-

nomial System, M be a polynomial of B such that

M(γ) ≡ 0 mod P and σ = deg

(M). Let A,B be two

elements expressed in the DPS B. If r and the poly-

nomial m satisfy

r > σ+deg

(λ) and deg

(m) > deg

(λ)+r (3)

then the polynomial R output by the Algorithm 2 is

expressed in the DPS B.

Proof. From the Deﬁnition 1, the polynomial R be-

longs to the DPS B = (P,γ,n,r,λ) if deg

R < n and

if deg

(R) < r. The fact that deg

R < n is easy to see

since all the computation in the Algorithm 2 are done

modulo E = Y

−λ.

Hence, we have only to prove that deg

R < r.

Since by deﬁnition deg

A,deg

B < r we have the fol-

lowing inequalities

deg

R = deg

((A ×B + Q ×M) mod E)/m

≤ max(deg

A + deg

B,deg

Q + deg

+deg

λ −deg

≤ max(2r,σ + deg

m) + deg

λ −deg

According to our hypothesis in the equation (3), we

have both 2r + deg

λ −deg

m < r and σ + deg

m +

deg

λ −deg

m < r. Hence, we get deg

(R) < r as

required.

4 CONSTRUCTION OF THE

POLYNOMIAL M

The result of this section uses mathematical structures

involving module over the polynomial ring F

[t] in

order to prove existence of a suitable polynomial M.

The remaining of the paper is independent from this

section and readers who are not familiar with such

mathematical structure can skip this section without

misunderstanding.

Our goal is to construct a polynomial M such that

M(t,γ) ≡ 0 mod P and deg

M is small. This polyno-

mial belongs to the set

M = {A(t,Y) ∈ F

[t,Y ] with deg

A < n}.

The set M has a natural structure of F

[t] module.

Recall that an F

[t]-module M is an (additive) abelian

group, with a scalar multiplication over F

[t]:

[t] ×M → M .

In order to calculate the element M with low de-

gree in t, we will use a sub-module M

of M spanned

by the following linearly independent vectors.

Ω =







P 0 0 ... 0

−γ 1 0 . .. 0

−γ

0 1 ... 0

−γ

n−1

0 0 ... 1







← P

←Y −γ

←Y

−γ

←Y

n−1

−γ

n−1

Each of the polynomials V(t,Y ) deﬁned by the rows

of Ω satisfy V (t,γ) ≡0, and any F

[t]-linear combina-

tion of these polynomials satisﬁes also this property.

Therefore, one way to construct M consists to com-

pute a minimal basis of M

and deﬁne M as the basis

element with the smaller degree in t. The notion of

minimality is related to the degree in t of the basis

elements.

According to polynomial matrix properties, one

can ﬁnd a minimal basis of Ω by computing its ma-

trix reduced form called the Popov form (Mulders and

Storjohann, 2003). In particular, the properties of the

Popov form (Villard, 1996, §1.2) tell us that there ex-

ists a minimal basis ( f

, f

,..., f

) of M

which sat-

isﬁes the following degree properties:

∑

i=1

deg

= deg

(det(Ω)) (4)

deg

≤ deg

≤ ... ≤ deg

(5)

If we set M = f

then the degree in t of M is min-

imal and satisﬁes the degree bound

deg

M ≤ (deg

P)/n (6)

Indeed, according to equations (4) and (5), we

have n ×deg

M <

∑

i=1

deg

and since det(Ω) =

P(t) we get the announced bound.

Beside the fact that the calculation of M is only

needed once at the construction of the DPS rep-

resentation, one would need to efﬁciently compute

such polynomial. This can be achieve within a com-

plexity of O(n

) binary operations with Algorithm

WeakPopovForm of (Mulders and Storjohann, 2003)

or with an asymptotic complexity of O(n

klog k) bi-

nary operations with Algorithm ColumnReduction of

(Giorgi et al., 2003).

5 DPS-LAGRANGE

MULTIPLICATION

In this section, we present a version of Algorithm 2

using a Lagrange representation of the DPS elements.

SECRYPT 2007 - International Conference on Security and Cryptography

232

5.1 Lagrange Representation

Let R a ring, and R [Y ] the polynomial ring over R .

The Lagrange representation of a polynomial of de-

gree n −1 in R [Y] is given by its values at n dis-

tinct points. For us, these n points will be the roots

of a polynomial E =

∏

i=1

(Y −α

) ∈ R [Y ]. From an

arithmetic point of view, this is related to the Chinese

Remainder Theorem which asserts that the following

application is an isomorphism

R [Y ]/(E(Y ))

−→

∏

i=1

R [Y ]/(Y −α

) (7)

A 7−→ (A mod (Y −α

))

i∈{1,...,n}

The computation of A mod (Y −α

) is simply the

computation of A(α

). In other words, the image of

A(Y ) by the isomorphism (7) is nothing else than the

multi-points evaluation of A at the roots of E. This

fact motivates the following Lagrange representation

of the polynomials.

Deﬁnition 2 (Lagrange representation). Let A ∈R [Y ]

with degA < n, and α

,..., α

be the n distinct roots

of a polynomial E(Y).

E(Y ) =

∏

i=1

(Y −α

) mod m

If a

= A(α

) for 1 ≤ i ≤ n, the Lagrange repre-

sentation (LR) of A(Y) is deﬁned by LR(A(Y )) =

,..., a

Lagrange representation is advantageous to per-

form operations modulo E: this is a consequence of

the Chinese Remainder Theorem. Speciﬁcally the

arithmetic modulo E in classical polynomial repre-

sentation can be costly if E has a high degree. In

LR representation this arithmetic is decomposed into

n independent arithmetic units, each does arithmetic

modulo a very simple polynomial (X −α

). Further-

more, arithmetic modulo (X −α

) is the arithmetic in

R since the product of two zero degree polynomials

is just the product of the two constant coefﬁcients.

5.2 Multiplication Algorithm

Let us go back to the Algorithm 2 and see how to use

Lagrange representation to perform polynomial arith-

metic in each step. The ﬁrst two steps can be done

in Lagrange representation modulo m

(t) such that E

split modulo m

(t):

E =

∏

i=1

(Y −α

) mod m

(t),

The third step must be done modulo a second

polynomial m

(t), which also splits E =

∏

i=1

(Y −

) mod m

(t), since the division by m

cannot be

performed modulo the polynomial m

(t).

We then need to represent the polynomials A and

B in Algorithm 2 with both their Lagrange represen-

tations modulo m

(t) and m

(t).

Notation 1. We will use in the sequel the following

notation. For a polynomial A of degree n −1 in Y we

will denote

• A the Lagrange representation in α

modulo m

(t)

• A the Lagrange representation in α

modulo m

(t).

Hence, we can do the following modiﬁcations to

the Algorithm 2:

Algorithm 3: DPS-LR Multiplication.

Input : A, A,B,B

Data : M such that M(t,γ) ≡ 0 mod P, M

such that M

= −M

−1

(mod E,m

Output:

R,R such that R ∈ B and R(t,γ) =

A(t,γ)B(t, γ)m

−1

mod P(t)

begin

Q ← A×B ×M

;

Q ←Convert

→m

(Q);

R ← (A×B) + Q ×M) ×m

−1

;

R ←Convert

→m

(R);

end

The operations to compute Q and R are performed

in Lagrange representation and then can be easily par-

allelized. It consists of n independent multiplications

in F

[t]/(m

(t)) and F

[t]/(m

(t)).

The major drawback of this algorithm is the con-

versions between Lagrange representations modulo

and m

. It is necessary to perform these opera-

tions efﬁciently in order to get a multiplier yielding

our announced space complexity.

5.3 Conversion

In order to provide an efﬁcient implementation of

conversions between Lagrange representations mod-

ulo m

and m

, we rely on the binomial form of

E = Y

−λ. Indeed, if µ

= α

is a root of E mod-

ulo m

then all others roots can be written

= µ

mod m

where ω

is a n-th primitive root of unity in

[t]/(m

). This property comes from the fact that

(α

/µ

)

= 1 mod m

and thus there exists an inte-

ger i such that α

/µ

= ω

mod m

. This is still true

SUBQUADRATIC BINARY FIELD MULTIPLIER IN DOUBLE POLYNOMIAL SYSTEM

233

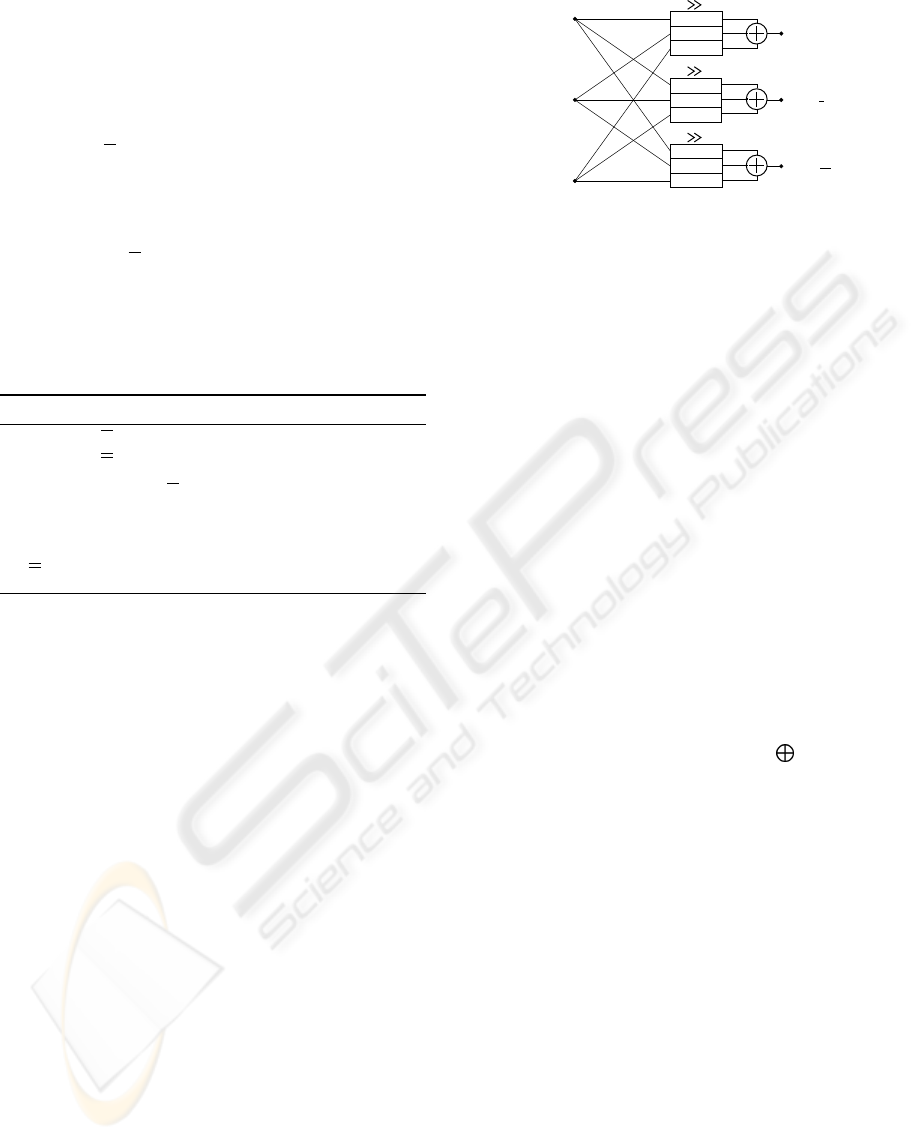
modulo m

. Thus, the multi-point evaluation of the

polynomial A(Y) in α

modulo m

can be done as fol-

low :

1. set

A(Y ) = A(µ

−1

Y) =

n−1

∑

i=0

−i

2. compute A = DFT

(

A,n,ω

where DFT

(

A,n,ω

) is the evaluations of the poly-

nomial

A in the n-th roots of unity ω

Similarly the Lagrange interpolation which com-

pute A(Y ) from A can be done by reversing the previ-

ous process.

By gluing together this two processes we get the

following algorithm to perform conversion between

Lagrange representations.

Algorithm 4: Convert

→m

Input : A

Output: A

A(Y ) ←DFT

−1

(A,n,ω

) ;

A(Y ) ←

A(µ

−1

Y) mod m

;

A(Y ) ←A(µ

Y) mod m

;

A ← DFT

(

A(Y ),n,ω

);

As a consequence, the conversion has a cost of

two Discrete Fourier Transforms. This can be done

efﬁciently by using FFT algorithm (Gathen and Ger-

hard, 1999, §8.2).

6 ARCHITECTURE FOR FFT

COMPUTATION

We present an architecture to perform the FFT calcu-

lation of a polynomial A(Y) ∈ R [Y] of degree n −1,

keeping in mind our targeted Lagrange conversion

algorithm. We consider the ring R = F

[t]/(m(t))

where m(t) = t

2n/3

n/3

+1 and n = 3

. Note that the

FFT process needs to be performed using the ternary

method since the binary one is not feasible over char-

acteristic 2 rings (Schonhage, 1977).

Let us denote ω a primitive n-th root of unity mod-

ulo m(t) and θ = ω

n/3

a 3rd root of unity. The ternary

FFT process is based on the following three-way split-

ting of A

∑

n/3−1

j=0

3 j

∑

n/3−1

j=0

3 j+1

3 j

∑

n/3−1

i=0

3 j+2

3 j

such that A = A

+YA

2(i + n/3)

i + n/3

2i + n/3

i + 2n/3

A[i +

]

A[i +

]

A[i]

[i]

Figure 1: Ternary butterﬂy operator.

Let

A[i] = A(ω

) be the i-th coefﬁcient of

DFT

(A,n,ω). Let us also denote by

[i],

[i] and

[i] the coefﬁcients of the DFT of order n/3 of re-

spectively A

and A

The following relations can be obtained by evalu-

ating A = A

+YA

in ω

,ω

i+n/3

and ω

i+2n/3

A[i] =

[i] + ω

[i],

A[i + n/3] =

[i] + θω

[i] + θ

[i], (8)

A[i + 2n/3] =

[i] + θ

[i] + θω

[i].

This operation is frequently called the butterﬂy

operation. It can be performed efﬁciently if we com-

pute modulo m(t)(t

n/3

+ 1) = t

+ 1 instead of m(t).

Indeed, in this case ω = t and a multiplication a(t) ×

modulo t

+1 is a simple cyclic shift. The butterﬂy

circuit (Figure 1) is a consequence of this remark and

the relations given in (8).

In Figure 1, the  blocks refer to a simple shift

operations by the given value and the blocks refer

to XOR operator. When no value is given, then shift

operation is not performed.

Within the FFT, the computations of

and

are done in the same way. These polynomials are

split in three parts and butterﬂy operations are applied

again. This process is done recursively until constant

polynomial are reached.

If we entirely develop this recursive process we

obtain the schematized architecture in Figure 2.

Let us now evaluate the complexity of this archi-

tecture. It is composed of log

(n) stages where each

stage consists of n/3 butterﬂy operations. Each of

these butterﬂy operations requires 6n XOR gates, and

has a delay of 2T

, where T

is the delay of one XOR

gate. Consequently, this architecture has a space com-

plexity of

S(FFT

m(t)

) = (2nlog

(n) + n) XOR (9)

and a delay of

D(FFT

m(t)

) = (2log

(n) + 1)T

. (10)

SECRYPT 2007 - International Conference on Security and Cryptography

234

reverse bit ordering

... ... ... ... ... ... ... ... ...

coefficients reduction

s stages FFT

s−1

butterﬂies

s−2

butterﬂies 3

s−2

butterﬂies 3

s−2

butterﬂies

A[0] , A[1] , A[2] , . .. , A[3

−3] , A[3

−2] , A[3

−1]

A[0] ,

A[1] ,

A[2] , ... ,

A[3

−3] ,

A[3

−2] ,

A[3

−1]

Figure 2: Ternary FFT circuit.

7 ARCHITECTURE AND

COMPLEXITY

We now present a hardware architecture associated to

Algorithm 3 in the special case where m

= t

1 and m

= t

2n/3

n/3

+ 1. This choice enables us to

use the FFT circuit presented in the previous section.

The architecture of our binary ﬁeld multiplier is given

in Figure 3. It is constituted of FFT blocks and multi-

pliers modulo m

(t) and m

(t).

Table 3: Complexity of multipliers modulo m

and m

Mul

Space Time

#AND 3n

log

(6)

#XOR

log

(6)

−9n −7/5 3 log

(n) + 3

Mul

Space Time

#AND

log

(6)

#XOR

log

(6)

−n/5 + n −1 3 log

(n)

These multipliers are referenced by blocks Mul

and Mul

in our architecture. Because of the special

form of m

(t) and m

(t) we can use the multiplier of

Fan and Hasan (Fan and Hasan, 2007) to perform this

operation. Therefore, the complexity (cf. Table 3) of

these blocks are easily deduced from (Fan and Hasan,

2007, Table 1).

The FFT blocks are designed using the ternary

method presented in previous section. Therefore,

their complexity are those given in (9) and (10). The

complexity of our multiplier can be evaluated with re-

spect to the numbers of each blocks and their cor-

responding space complexity denoted S , and time

complexity denoted D. For the space complex-

ity this gives 4nS (Mul

) + 5nS (Mul

) + 2S (FFT

) +

−1

−(n−1)

n−1

−(n−1)

n−1

FFT

n−1

−1

Mul

−1

Mul

A ×B ×M

convert

→m

FFT

n−1

FFT

Mul

n−1

−1

(A ×B + Q ×M)m

−1

convert

→m

Figure 3: DPS-Lagrange Multiplier.

2S(FFT

) + 2n

/3 XOR. Similarly, the critical path

of this architecture gives the delay 4D(Mul

) +

4D(Mul

) + 2D(FFT

) + T

Using these expressions, (9),(10) and Table 3, we

can compute the complexity with respect to the num-

ber of XOR and AND gates and their corresponding

delay T

and T

Let r be the degree in t of the coefﬁcients in

the DPS representation then deg

) must satisfy

deg

) ≥ r. Therefore, this implies that k ≤ r×n =

/3 and thus leads to use n ≈

√

k, where k is the

degree of the ﬁeld F

Finally, we obtain the complexity of the DPS-

Lagrange multiplier stated in Table 4. We also give in

this table the complexity of the best known method,

regarding space and time complexity, to perform bi-

nary ﬁeld multiplication. One can remark that our ap-

proach decrease the space complexity from k

1.58

1.31

, while it is slower by a factor roughly equals to

5.3.

SUBQUADRATIC BINARY FIELD MULTIPLIER IN DOUBLE POLYNOMIAL SYSTEM

235

Table 4: Complexity comparison.

Space Complexity Time Complexity

Method # AND # XOR T

This paper 14.5k

1.31

69.6k

1.31

−31k + k

0.5

(8log

(k) + 39) 8 16log

(k) + 20

∗

binary k

1.58

5.5k

1.58

−5k −0.5 1 2log

(k) + 1

∗

ternary k

1.63

4.8k

1.63

−4k −0.8 1 3log

(k) + 1

∗

= (Fan and Hasan, 2007);

8 CONCLUSION

In this paper we have presented a novel algorithm to

perform multiplication in binary ﬁeld, using a Dou-

ble Polynomial System of representation. This system

enables the use of Fast Fourier Transform in the mul-

tiplication according to Lagrange representation. The

resulting multiplier still achieves a logarithmic time

complexity, but asymptotically improves the space

complexity from O(k

1.58

) to O(k

1.31

Our method is a ﬁrst approach to reduce the space

complexity of binary ﬁeld multiplier. In particular,

some optimizations can be done to reduce the con-

stant factors in the complexity. For example, a lot of

multiplications by a constant are counted as full mul-

tiplication in the current complexity evaluation.

Furthermore, one can also reduce the exponent

in the space complexity by replacing Fan and Hasan

multipliers with a quasi-linear approach (e.g. Schön-

hage’s technique (Schonhage, 1977)).

REFERENCES

Berlekamp, E. (1982). Bit-serial Reed-Solomon encoder.

IEEE Transactions on Inf. Th., IT-28.

Difﬁe, W. and Hellman, M. (1976). New directions in cryp-

tography. IEEE Transactions on Information Theory,

24:644–654.

Fan, H. and Dai, Y. (2005). Fast bit-parallel GF(2

) mul-

tiplier for all trinomials. IEEE Trans. on Comp.,

54(4):485–490.

Fan, H. and Hasan, A. (2007). A new approach to

subquadratic space complexity parallel multipliers

for extended binary ﬁelds. IEEE Trans. Comput.,

56(2):224–233.

Gao, S. (1993). Normal Bases over Finite Fields. Phd the-

sis, Waterloo University, Canada.

Gathen, J. v. and Gerhard, J. (1999). Modern Computer

Algebra. Cambridge University Press, New York, NY,

USA.

Giorgi, P., Jeannerod, C.-P., and Villard, G. (2003). On

the complexity of polynomial matrix computations.

In Proceedings of ISSAC’03, Philadelphia, Pennsyl-

vania, USA, pages 135–142. ACM Press.

Guajardjo, J. and Paar, C. (1997). Efﬁcient algorithms for

elliptic curve cryptosystems. In Advances in Cryp-

tology, Proceedings of Eurocrypt’97, volume 1233 of

LNCS, pages 342–356. Springer-Verlag.

Hasan, M., Wang, M., and Bhargava, V. (1993). A Mod-

iﬁed Massey-Omura Parallel Multiplier for a Class

of Finite Fields. IEEE Transactions on Computeurs,

42(10):1278–1280.

J.-C. Bajard, L.Imbert, T. P. (2005). Modular num-

ber systems: Beyong the mersenne family. In

SAC’04,Waterloo, Canada, volume 3357 of LNCS,

pages 159–169. Springer-Verlag.

Koblitz, N. (1987). Elliptic curve cryptosystems. Mathe-

matics of Computation, 48:203–209.

Mastrovito, E. (1991). VLSI architectures for computations

in Galois ﬁelds. PhD thesis, Dep.Elec.Eng.,Linkoping

Univ.

Miller, V. (1986). Use of elliptic curves in cryptogra-

phy. In Advances in Cryptology, proceeding’s of

CRYPTO’85, volume 218 of LNCS, pages 417–426.

Springer-Verlag.

Montgomery, P. L. (1985). Modular multiplication with-

out trial division. Mathematics of Computation,

44(170):519–521.

Mulders, T. and Storjohann, A. (2003). On lattice reduction

for polynomial matrices. Journal of Symbolic Compu-

tation, 35(4):377–401.

Schonhage, A. (1977). Schnelle multiplikation von poly-

nomen uber korpern der charakteristik 2. Acta Infor-

matica, 7:395–398.

Villard, G. (1996). Computing Popov and Hermite forms

of polynomial matrices. In Proceedings of ISSAC’96,

Zurich, Suisse, pages 250–258. ACM Press.

SECRYPT 2007 - International Conference on Security and Cryptography

236