MOBILE SECRET KEY DISTRIBUTION

WITH NETWORK CODING

∗

Paulo F. Oliveira, Rui A. Costa and Jo

ao Barros

Instituto de Telecomunicac¸

oes

Departamento de Ci

encia de Computadores, Faculdade de Ci

encias da Universidade do Porto

Rua Campo Alegre, 1021/1055, 4169-007 Porto, Portugal

Keywords:

Sensor networks, secret key distribution, network coding, one-time pad.

Abstract:

We consider the problem of secret key distribution in a sensor network with multiple scattered sensor nodes

and a mobile device that can be used to bootstrap the network. Our main contribution is a practical scheme that

relies on network coding to provide a robust and low-complexity solution for sharing secret keys among sensor

nodes. In spite of its role as a key enabler for this approach, the mobile node only has access to encrypted

version of the keys. In contrast with probabilistic key pre-distribution schemes our method assures secure

connectivity with probability one, requiring only a modest amount of memory — initially each sensor node

stores only one key per secured link.

1 INTRODUCTION

Among the many security challenges posed by wire-

less sensor networks (WSNs), i.e. self-organizing col-

lections of sensing devices with processing and com-

munication capabilities, the generation and distribu-

tion of private keys for authentication and conﬁden-

tiality in pairwise or group communication is ar-

guably one of the most fundamental problems.

Currently available proposals can be divided into

at least three basic types of secret key distribution

schemes (Du et al., 2005): (a) trusted third party, (b)

public-key infrastructure and (c) key pre-distribution.

Trusted party schemes, e.g. SPINS (Perrig et al.,

2002), assume that a base station provides the sensor

nodes with secret keys that are encrypted with one in-

dividual key per sensor node. Although public-key in-

frastructure schemes have been implemented success-

fully in some sensor networks (Malan et al., 2004),

their demands in terms of processing and communi-

cation overhead are arguably too high, in particular

with respect to the power constraints imposed on this

type of devices. Key pre-distribution thus emerges as

a strong candidate, mainly because it requires consid-

∗

This work was partly supported by the Fundac¸

ao para

a Ci

encia e Tecnologia (Portuguese Foundation for Science

and Technology) under grant POSC/EIA/62199/2004.

erably less resources. The concept is elaborated in

(Eschenauer and Gligor, 2002), where a random pool

of keys P is selected from the key space prior to sen-

sor node deployment. Then, each node receives a key

ring, consisting of randomly chosen k keys from P. A

secure link is said to exist between two neighboring

sensor nodes, if they share a key with which commu-

nication may be initiated. A random graph analysis

in (Eschenauer and Gligor, 2002) shows that shared-

key connectivity can be achieved almost surely, pro-

vided that each sensor node is loaded with 250 keys

drawn out of a pool of roughly 100.000 sequences.

Using a different scheme with pre-installed key

rings, LEAP (Zhu et al., 2003) erases the network key

immediately after the pairwise keys are established.

Since nodes in that situation can no longer establish

pairwise keys, this protocol is only suitable for static

WSNs.

In the spirit of the Resurrecting Duckling

paradigm in ubiquitous computing (Stajano and An-

derson, 1999; Stajano, 2002), we consider the sce-

nario in which a mobile node, e.g. a handheld de-

vice or a laptop computer, is used to activate the net-

work and help establish secure connections between

the sensor nodes. We shall show that by exploiting the

beneﬁts of network coding (Fragouli et al., 2006; Deb

et al., 2005), as illustrated in Fig. 1, it is possible to

171

F. Oliveira P., A. Costa R. and Barros J. (2007).

MOBILE SECRET KEY DISTRIBUTION WITH NETWORK CODING.

In Proceedings of the Second International Conference on Security and Cryptography, pages 171-174

DOI: 10.5220/0002126801710174

 SciTePress

SA B

a⊕ ba⊕ b

Figure 1: A typical wireless network coding example. To

exchange messages a and b, nodes A and B must route their

packets through node S. Clearly, a traditional scheme would

require four transmissions. However, if S is allowed to per-

form network coding with simple XOR operations, a ⊕ b

can be sent in one single broadcast transmission (instead

one transmission with a followed by another one with b).

By combining the received data with the stored message, A

which possesses a can recover b and B can recover a using

b. Thus, network coding saves one transmission.

design power-efﬁcient key distribution schemes that

are not probabilistic, while ensuring that the afore-

mentioned mobile node does not constitute a single

point of attack — its capture does not compromise

the whole network.

Our main contribution is a practical secret key dis-

tribution scheme with efﬁcient use of resources —

in addition to a small number of transmissions and

low-complexity processing (mainly XOR operations),

each node is only required to pre-store a small num-

ber of keys (as many as its expected number of links).

Another feature of our approach is a “blind” key dis-

tribution — although the mobile node only has access

to encrypted versions of the secret keys, it is capable

of using network coding to ensure that each pair of

sensor nodes receives enough data to agree on a pair

of secret keys.

The rest of the paper is organized as follows. Sec-

tion 2 provides a detailed description of our secret key

distribution scheme. Section 3 then elaborates the at-

tacker model and proves that the mobile node is in-

deed ignorant about the pre-stored keys. The paper

concludes with Section 4.

2 MOBILE SECRET KEY

DISTRIBUTION

2.1 Key Distribution Scheme

Suppose that sensor nodes A and B want to establish

a secure link via a mobile node S. Although A and B

own different keys that are unknown to S, the latter

is capable of providing A and B with enough infor-

mation for them to recover each other’s keys based

on their own pre-stored keys. The basic scheme for

multiple nodes, which is illustrated in Fig. 2, can be

summarized in the following tasks:

(i) Prior to sensor node deployment:

– Generate a large pool

P of statistically in-

dependent keys K

and their identiﬁers i ∈

{0,...,|

P | − 1}; for simplicity, each global key

identiﬁer i is assumed to result from the con-

catenation of a node identiﬁer n and a local key

identiﬁer j (e.g. |n| = 24 bit and | j| = 8 bit);

– Produce a one-time pad R, i.e. a binary se-

quence of size equal to the key size and con-

sisting of bits drawn randomly according to a

Bernoulli (

) distribution;

– Store in the memory of S a list with all iden-

tiﬁers i and an encrypted version of the corre-

sponding key K

⊕ R (it shall be argued in Sec-

tion 3 that in this case it is perfectly safe to use

the same one-time pad R for all the keys, be-

cause they are drawn uniformly at random);

– Let C ≪ |

P | be the expected number of links

that each node intends to use during its lifetime;

load C keys into the memory of each sensor;

each sensor node knows both its own identiﬁer

n and the local key identiﬁers j.

(ii) After sensor node deployment:

1. The sensor nodes perform standard neighbor-

hood discovery by broadcasting their identiﬁers

n and storing in a list L

the identiﬁers an-

nounced by their neighbors;

2. S broadcasts HELLO messages that are re-

ceived by any sensor node within wireless

transmission range. Each sensor node sends a

reply message containing {n,L

};

3. Upon receiving {n(A), L

n(A)

} from a node A

and {n(B),L

n(B)

} from a node B, the mobile

node S checks whether n(A) ∈ L

n(B)

and n(B) ∈

n(A)

. If this is the case, S performs a simple

table look-up and runs a XOR network cod-

ing operation over the corresponding protected

keys, i.e. K

i(A)

⊕ R ⊕ K

i(B)

⊕ R. Since R

cancels out, S sends back {n(A) ∗ j(A), n(B) ∗

j(B),K

n(A)∗ j(A)

⊕ K

n(B)∗ j(B)

}, where (n(·) ∗

j(·)) denotes the concatenation of node and lo-

cal key identiﬁers; the local key identiﬁer j (for

each node) is initially set at 0 and increases with

the number of established links;

4. Based on the received XOR combination

n(A)∗ j(A)

⊕ K

n(B)∗ j(B)

, A and B can eas-

ily recover each other’s key by perform-

ing an XOR operation using the lowest lo-

cal key identiﬁer that corresponds to an un-

used key (A knows K

n(A)∗ j(A)

and computes

n(A)∗ j(A)

⊕ K

n(A)∗ j(A)

⊕ K

n(B)∗ j(B)

, thus obtain-

ing K

n(B)∗ j(B)

; B proceeds similarly).

Thus, each pair of nodes shares a pair of keys

which is kept secret from S.

SECRYPT 2007 - International Conference on Security and Cryptography

172

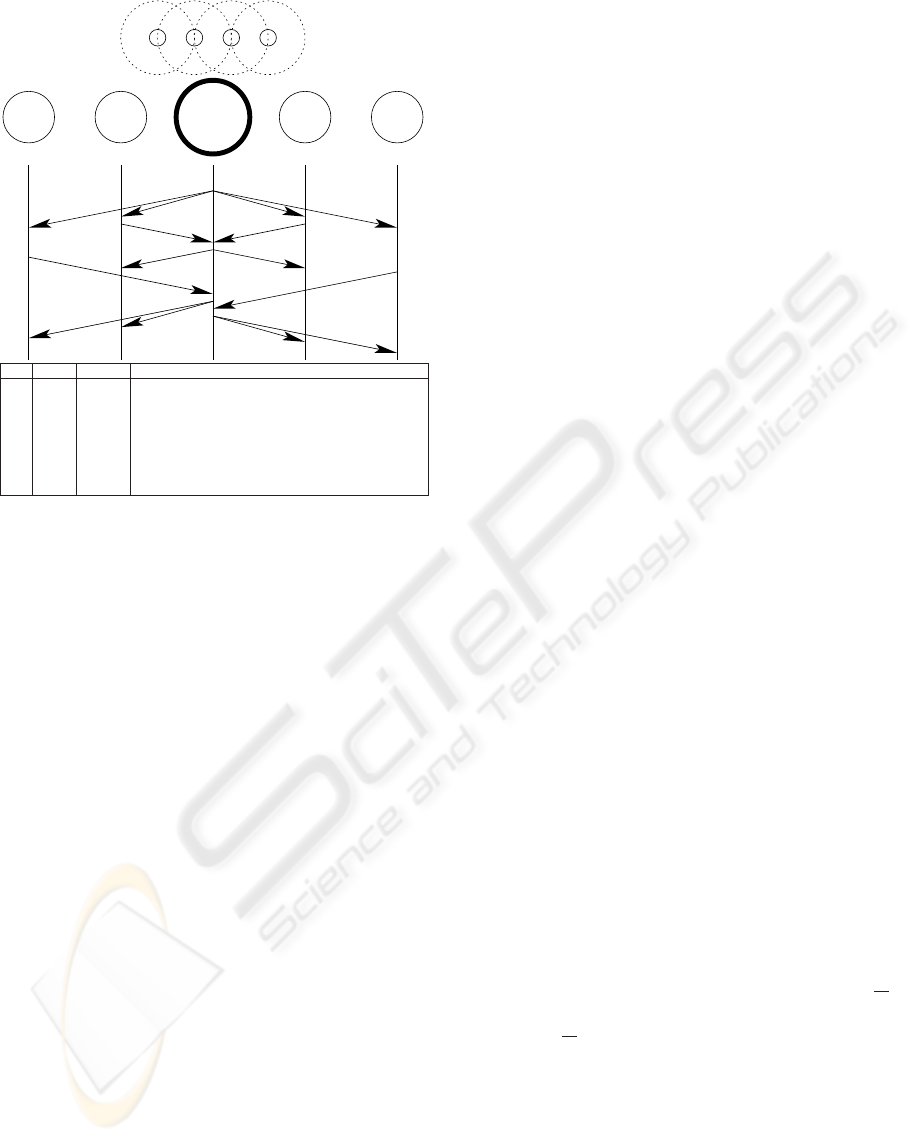
A B C D

SA B

msg sender receiver content

1 S A,B,C,D HELLO

2 B S {n(B),[n(A),n(C)]}

3 C S {n(C), [n(B), n(D)]}

4 S B,C {n(B) ∗ j(B), n(C) ∗ j(C), K

n(B)∗ j(B)

⊕ K

n(C)∗ j(C)

}

5 A S {n(A),[n(B)]}

6 S A,B {n(A) ∗ j(A),n(B) ∗ ( j(B) + 1),K

n(A)∗ j(A)

⊕ K

n(B)∗( j(B)+1)

}

7 D S {n(D),[n(C)]}

8 S C,D {n(C) ∗( j(C) +1),n(D) ∗ j(D), K

n(C)∗( j(C)+1)

⊕ K

n(D)∗ j(D)

}

Figure 2: Example of the general key distribution scheme

for the topology shown above. Sensor nodes A, B, C and

D want to exchange keys with their neighbors via a mobile

node S. Initially, the nodes exchange their identiﬁers and

wait for an HELLO message from S (transmission 1). After

this step, each node sends a key request message to the mo-

bile node (transmissions 2,3,5,7) and waits for the latter to

send back a key reply message (transmissions 4,6,8).

2.2 Usage of Keys

There are several ways to make use of the established

pair of keys. One alternative to the solution in which

each node encrypts messages with its own pre-stored

key and decrypts received messages with the neigh-

bor’s key, is to combine the two keys into a single key

through a boolean operation (e.g. or, and). Another

solution would be to encrypt the messages in a dou-

ble cypher using both keys, but this option requires

higher processing capability.

Perhaps the most effective option would be for the

nodes to use the two shared keys (one in each direc-

tion) to agree on a session key (e.g., node A generates

a random value a, encrypts it using one of the shared

keys and sends it to node B, which generates a ran-

dom value b and sends it back to A, encrypted with

the other key). The main advantage is that the sensor

nodes can secure their communications using the con-

catenation of the exchanged random values (ordered

by the key identiﬁers by which they were encrypted),

resulting in a shared key with double the size and a

considerable improvement in terms of security. Natu-

rally, the availability of suitable random number gen-

erators is a relevant issue to be taken under consider-

ation.

3 SECURITY PERFORMANCE

EVALUATION

3.1 Attacker Model

We assume two types of threats in our scheme: (1)

a passive attacker that listens to all the trafﬁc over

the wireless medium and (2) an active attacker who is

able to inject bogus data in the network. We assume

that the attacker can gain access to the memory of the

mobile node or to the memory of a limited number of

sensor nodes, but never to both. We consider that the

adversary computational resources are limited (poly-

nomial in the security parameter).

The ﬁrst type of attacker does not constitute a

threat because the keys cannot be decoded from the

XOR messages in the ether. The second type of attack

can be detected by the legitimate nodes, who ignore

any messages that are corrupted by an invalid key.

3.2 One-Time Pad Security

The keys stored in the mobile node are protected by

a one-time pad. It is well-known that the one-time

pad can be proven to be perfectly secure for any mes-

sage statistics if the key is (a) truly random, (b) never

reused and (c) kept secret. In our case, the messages

correspond to keys drawn from a uniform distribution

and, consequently, the requirement that the one-time

pad is never re-used can be dropped, as stated in the

following theorem.

Theorem 3.1 The knowledge of {K

⊕ R, K

⊕

R,...,K

⊕ R} does not increase the information that

the attacker has about any key, i.e., ∀i ∈ {1,...,m},

P(K

= x|K

⊕ R = y

,...,K

⊕ R = y

) = P(K

= x).

Sketch of proof First, notice that P(K

= x) =

We shall prove that P(K

= x|K

⊕ R = y

,...,K

⊕

R = y

) =

,∀i ∈ {1, ..., m}, which yields the result.

P(K

= x|K

⊕ R = y

,..., K

⊕ R = y

)

= P(K

= x|K

⊕ K

= y

⊕ y

,..., K

⊕ K

= y

⊕ y

where the event K

⊕ K

= y

⊕ y

is not present, be-

cause it is redundant. Let z

= y

⊕ y

, for 1 ≤ j ≤ m

and j 6= i. Let A denote the event {K

= x} and B de-

note the event {K

⊕K

= z

,...,K

⊕K

= z

}. Then,

P(K

= x|K

⊕ K

= z

,...,K

⊕ K

= z

) = P(A|B).

MOBILE SECRET KEY DISTRIBUTION WITH NETWORK CODING

173

We already have seen that P(A) = P(K

= x) =

1/2

. We have that:

P(B|A) = P(K

⊕ K

= z

,...,K

⊕ K

= z

= x)

∏

j=1

P(K

= z

⊕ x) =

n(m−1)

P(B) = P(K

⊕ K

= z

,...,K

⊕ K

= Z

)

∏

j=1

P(K

⊕ K

= z

) =

n(m−1)

Therefore, we have that P(A|B) =

n(m−1)

3.3 Memory Requirements

We recall that each node n has C keys K

in memory,

each one identiﬁed by |i| = |n| + | j| bits, where | · | de-

notes the size of the argument. To store the protocol

data, each node requires |n| + C ∗ (| j| + |K

|) bits of

memory space and the mobile node needs 2

|i|

∗ (|i| +

|) = |

P | ∗ (⌈log

(|P |)⌉ + |K

|) bits. For example, if

we assign n = 24 there is space for 16.777.216 differ-

ent node identiﬁers. For j = 8, each sensor node can

obtain 256 keys (e.g. if each node initially has C = 20

keys in its memory, there is space for 246 extra keys).

Table 1 illustrates the required resources, which we

deem very reasonable under current technology.

Table 1: Required memory for each sensor node (SN) and

required memory for the mobile node (MN), for ﬁxed values

of n = 24, j = 8 and C = 20.

| Size on SN Size on MN

128 bit 343 Bytes 80.0 GB

64 bit 183 Bytes 48.0 GB

32 bit 103 Bytes 32.0 GB

We omit the details of our implementation on

TelosB motes due to lack of space.

4 CONCLUSIONS

We presented a secret key distribution scheme for

large sensor networks. Unlike (Eschenauer and

Gligor, 2002) and (Du et al., 2005), this is not a prob-

abilistic scheme, i.e. any two nodes that can reach

each other can communicate securely with probabil-

ity one, using a small number of pre-stored keys and

without the need for establishing path-keys albeit at

the expense of a mobile node for bootstrapping. Since

our protocol and its extensions can easily accommo-

date for additional nodes, new keys and secured links,

we deem the proposed network coding approach to be

well suited for dynamic sensor networks with strin-

gent memory and processing restrictions. Extensions

for group keys, extra keys request and revocation can

be implemented and will be reported elsewhere.

Although our use of network coding was limited

to XOR operations, more powerful schemes are likely

to result from using linear combinations of the stored

keys. Investigating the potential of random linear net-

work coding (Lima et al., 2007) in the context of se-

cret key distribution is one of the main objectives of

our ongoing work.

REFERENCES

Deb, S., Effros, M., Ho, T., Karger, D., Koetter, R., Lun, D.,

Medard, M., and Ratnakar, N. (2005). Network cod-

ing for wireless applications: A brief tutorial. Proc. of

IWWAN, London, UK, May.

Du, W., Deng, J., Han, Y. S., Varshney, P. K., Katz, J.,

and Khalili, A. (2005). A pairwise key predistribution

scheme for wireless sensor networks. ACM Trans. Inf.

Syst. Secur., 8(2):228–258.

Eschenauer, L. and Gligor, V. D. (2002). A key-

management scheme for distributed sensor networks.

In CCS ’02: Proceedings of the 9th ACM conference

on Computer and communications security, pages 41–

47, New York, NY, USA. ACM Press.

Fragouli, C., Boudec, J.-Y. L., and Widmer, J. (2006). Net-

work coding: an instant primer. SIGCOMM Comput.

Commun. Rev., 36(1):63–68.

Lima, L., M

edard, M., and Barros, J. (2007). Random Lin-

ear Network Coding: A Free Cipher? In Proc. of the

IEEE International Symposium on Information The-

ory (ISIT).

Malan, D., Welsh, M., and Smith, M. (2004). A public-

key infrastructure for key distribution in tinyos based

on elliptic curve cryptography. In First IEEE Interna-

tional Conference on Sensor and Ad Hoc Communi-

cations and Network, Santa Clara, California.

Perrig, A., Szewczyk, R., Tygar, J. D., Wen, V., and Culler,

D. E. (2002). SPINS: Security protocols for sensor

networks. Wireless Networks, 8(5):521–534.

Stajano, F. (2002). Security for Ubiquitous Computing.

John Wiley and Sons.

Stajano, F. and Anderson, R. J. (1999). The resurrect-

ing duckling: Security issues for ad-hoc wireless net-

works. In Christianson, B., Crispo, B., Malcolm, J. A.,

and Roe, M., editors, Security Protocols Workshop,

volume 1796 of Lecture Notes in Computer Science,

pages 172–194. Springer.

Zhu, S., Setia, S., and Jajodia, S. (2003). LEAP: efﬁcient

security mechanisms for large-scale distributed sensor

networks. In CCS ’03: Proceedings of the 10th ACM

conference on Computer and communications secu-

rity, pages 62–72, New York, NY, USA. ACM Press.

SECRYPT 2007 - International Conference on Security and Cryptography

174