ON THE EFFECT OF SCORE EQUALIZATION

IN SVM MULTIMODAL BIOMETRIC SYSTEMS

Pascual Ejarque and Javier Hernando

TALP Research Center, Department of Signal Theory and Communications

Technical University of Catalonia, Barcelona, Spain

Keywords: Normalization, Equalization, Histogram, Bi-Gaussian, Support Vector Machines, Multimodal.

Abstract: Most Support Vector Machine (SVM) based systems make use of conventional methods for the

normalization of

the features or the scores previously to the fusion stage. In this work, in addition to the

conventional methods, two equalization methods, histogram equalization, which was recently introduced in

multimodal systems, and Bi-Gaussian equalization, which is presented in this paper, are applied upon the

scores in a multimodal person verification system composed by prosodic, speech spectrum, and face

information. The equalization techniques have obtained the best results; concretely, Bi-Gaussian

equalization outperforms in more than a 22.19 % the results obtained by Min-Max normalization, the most

used normalization technique in SVM fusion systems. The prosodic and speech spectrum scores have been

provided by speech experts using records of the Switchboard I database and the face scores have been

obtained by a face recognition system upon XM2VTS database.

1 INTRODUCTION

Multimodal score fusion can be performed in two

main approaches: the arithmetical or logical

combination of the scores and the classification of

the score vectors by mean of classificatory

techniques (Bolle et al., 2004). In the combinatory

approach the scores provided by every monomodal

system must be normalized before the fusion process

due to, without this process, the contribution of a

biometric could eliminate the contribution of the rest

of the experts (Jain et al., 2005). In the classificatory

approach, not much importance has been given to

score normalization because the same classificatory

techniques can adapt themselves to the biometrical

scores characteristics.

Concretely, for the SVM based classificatory

techniques

, the usage of kernels permits the non

linear transformation of the input scores in a higher

dimensional subspace where the recognition

decision can be taken by means of a separator

hyperplane (Cristianini and Shawe-Taylor, 2000).

Some efforts have been made for the development of

particular kernels for each application, as in the case

of spherical normalization developed by Wan et al.

(Wan and Renals, 2005). However, most

investigators and developers use well-known kernels

as radio basis function (RBF) or polynomial kernels

for their systems and adapt them by the modification

of the kernel parameters. In this case, the number of

non linear transformations is limited by the kernel

and the chosen parameters.

The aim of this work is to demonstrate the

portance of the normalization of the monomodal

scores in an SVM fusion system and, more

concretely, the application of two equalization

techniques, histogram equalization and Bi-Gaussian

equalization, which have outperformed the results

obtained by the conventional normalization

methods. Histogram equalization consists in the

equalization of the probability density function

(PDF) to a reference signal and has recently been

introduced in multimodal systems (Farrús et al.,

2006; Ejarque et al., 2007). Bi-Gaussian

equalization, which has obtained the best results, is

presented in this work and equalizes the PDF to a

double gaussian with the same EER than the original

modality.

The multimodal system is composed by three

score s

ources: the first score is obtained by the SVM

fusion of 9 voice prosodic features (Wolf, 1972;

Farrús et al., 2006), the second one is obtained by a

voice spectrum expert based in the Frequency

Ejarque P. and Hernando J. (2007).

ON THE EFFECT OF SCORE EQUALIZATION IN SVM MULTIMODAL BIOMETRIC SYSTEMS.

In Proceedings of the Second International Conference on Security and Cryptography, pages 33-38

DOI: 10.5220/0002130000330038

 SciTePress

Filtering front-end and GMM (Nadeu et al., 1996),

and the last one is provided by an NMFFaces

algorithm (Tefas et al., 2005) face recognition

system. A chimerical database has been created from

the prosodic and spectrum scores obtained from

voice signals of the Switchboard-I database and

from the scores obtained from the face still images

of the XM2VTS database.

The results obtained in the SVM fusion system

with the equalization techniques outperform that

obtained with the conventional methods with RBF

kernel.

The paper is organized as follows: in section 2,

the normalization techniques that have been tested in

this work are presented; in section 3 the equalization

methods are presented; in section 4 the SVM

classificatory technique is reviewed and finally; in

sections 5 and 6, the results and conclusions are

presented.

2 NORMALIZATION METHODS

The normalization process transforms the

monomodal scores of all the biometrics in a

comparable range of values and is an essential step

in multimodal fusion. The most conventional

normalization techniques are Min-Max, Z-Score,

and Tanh, which have been widely used in previous

works (Bolle et al., 2004; Jain et al., 2005).

2.1 Min-Max Normalization (MM)

Min-Max normalization maps the scores in the [0, 1]

range by means of an affine transformation. The

calculation in equation 1 must be applied upon the

multimodal scores a, where min(a) and max(a) are

the minimum and maximum values of the

monomodal scores.

2.2 Z-Score Normalization (ZS)

By means of Z-Score normalization the mean of all

the biometric scores is set to 0 and its variance is set

to 1 in a non affine transformation. In this case, the

normalization affects to the global statistics of the

scores. Equation 2 demonstrates the application of

this normalization:

where mean(a) and std(a) are respectively the

statistical mean and variance of a monomodal set of

scores.

2.3 Hyperbolic Tangent Normalization

(TANH)

Tanh normalization maps the scores in the [-1, 1]

range in a non linear transformation. By the

application of this technique the values around the

mean of the scores are transformed by a linear

mapping and a compression of the data is performed

for the high and low values of the scores. This

normalization is performed by means of the formula

in equation 3

where μ

and σ

are, respectively, the mean and

standard deviation estimates, of the genuine score

distribution introduced by Hampel (Jain et al., 2005)

and k is a suitable constant. The main advantage of

this normalization is the suppression of the effect of

outliers, which is absorbed by the compression of

the extreme values.

3 EQUALIZATION

In this section, two equalization techniques are

presented: histogram equalization, which has

recently been integrated in multimodal person

recognition systems (Farrús et al., 2006; Ejarque et

al., 2007), and Bi-Gaussian equalization, which is

presented in this paper. These techniques have been

used as normalization methods in this work.

3.1 Histogram Equalization (HEQ)

By means of histogram equalization, the cumulative

distribution function of the monomodal biometrics is

equalized to a distribution of reference. This non-

linear technique has been widely used in image

treatment (Jain, 1986) and has been applied to

speech treatment in order to reduce non linear

effects introduced by speech systems such as:

microphones, amplifiers, etc. (Balchandran and

Mammone, 1998).

()

() ()

min

max min

−

(1)

()

ameana

std a

−

(2)

tanh 1

TANH

⎧

⎫

⎛⎞

−

⎪

⎨

⎬

⎜⎟

⎪

⎝⎠

⎩⎭

(3)

SECRYPT 2007 - International Conference on Security and Cryptography

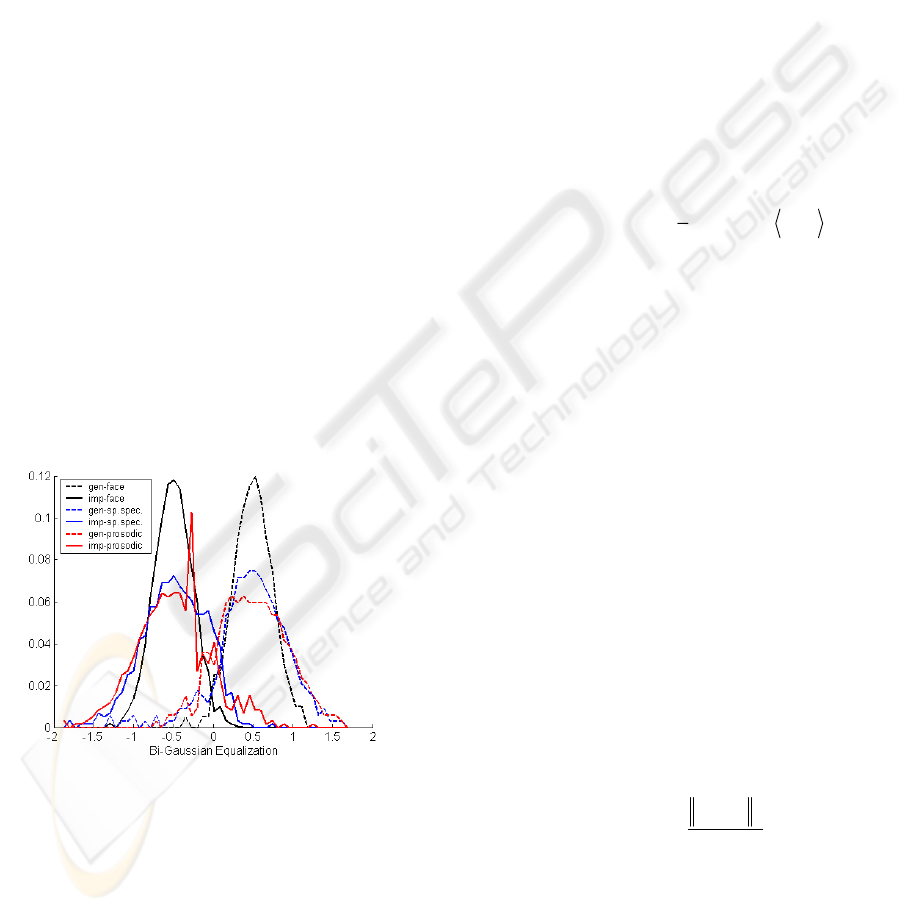
The authors have used histogram equalization as

a normalization technique in combinatory score

fusion systems in several works (Farrús et al., 2006;

Ejarque et al., 2007) with good results. In the

experiments presented, all the biometrics have been

referenced to that with the best monomodal

recognition result, the face system.

3.2 Bi-Gaussian Equalization (BGEQ)

With this normalization technique the scores of each

monomodal biometric are equalized to a double

Gaussian distribution that would obtain the same

EER (Equal Error Rate) than the original scores. In

fact, histogram equalization is applied upon the

monomodal scores where the reference distribution

is artificially built by the combination of two

Gaussians with the same variance, one for the client

scores and another one for the impostor scores. The

mean of the client Gaussian is set to a half and the

impostor one is set to minus a half.

As in the case of histogram equalization, this

technique equalizes the whole monomodal

distributions. However, in this case, the elimination

of the effect of outliers is granted. Furthermore, the

mean of the genuine and impostor scores have the

same value as it can be seen in figure 1 where

histogram of the scores for Bi-Gaussian equalization

is plotted.

Figure 1: Histogram of the scores for BGEQ.

4 SVM SCORE FUSION

Support Vector Machines (SVM) are learning

classificatory kernel-based methods: learning

because the whole training data and not only some

statistical information is used for the training of the

SVM models, classificatory because a SVM system

performs a two-class classification of the data by

means of a hyperplane, and kernel-based because the

addition of a kernel in the system permits to make

the classification of the data in a higher dimensional

space (Cristianini and Shawe-Taylor, 2000).

In a multimodal fusion verification system, SVM

techniques aim to decide in the genuine-impostor

disjuncture. Multimodal score vectors are created

from the monomodal data which is used as the input

data of the SVM based system. During the training

phase, the normal vector w and the bias b of the

hyperplane are determined according to the

minimization of ||w||

subject to y

(<w, x

>+b)≥1

where x

are the training score vectors and y

are 1

for the genuine and -1 for the impostor training

vectors.

The dual representation of this problem is

presented in equation 4:

where α

are the Lagrangian multipliers, and the bias

can be found from y

(<w, x

>+b)=1 where α

≠ 0.

The extension to soft margin classifiers permits

the introduction of the regularization parameter C,

which controls the trade off between allowing

training errors and forcing rigid margins. The dual

representation restriction α

≥ 0 is converted in the

soft margin classification to 0 ≤ α

≤ C.

The dot product of the multimodal score vectors

in equation 4 can be replaced by a kernel, which

must accomplish Mercer’s conditions (Cristianini

and Shawe-Taylor, 2000). The use of a kernel

transports the data to a higher dimensional space

where the classificatory hyperplane is defined.

One of the most usually used kernel is radio

basis function (RBF), which is based in Gaussian

classificatory regions and correspond to the formula

in equation 5 where the parameter σ controls the

variance of the Gaussian functions, that is, the width

of the regions.

When an RBF kernel is used in the classificatory

process, the information used by the SVM system is

the distance between the score vectors. For this

reason, great differences in the range of values

covered by the different monomodal scores could

produce classificatory errors, due to the contribution

()

maximize ,

subject to 0, 0

iijiji

iij

ii i

αα αα

αα

=−

=≥

∑∑

∑

yxx

(4)

()

,exp

kxx

⎛⎞

−

⎜

=−

⎜

⎝⎠

⎟

(5)

ON THE EFFECT OF SCORE EQUALIZATION IN SVM MULTIMODAL BIOMETRIC SYSTEMS

of some of the monomodal systems can be

eliminated by other ones.

To avoid this type of problem, the use of a

normalization process can be useful and most SVM

based systems incorporate a Min-Max normalization

previous to the classificatory system. In this work,

the effect of several normalization techniques upon a

SVM multimodal system is explored.

5 EXPERIMENTS

In this section, the speaker and face recognition

systems used in the fusion experiments and the

experimental results obtained with the different

normalization methods in an SVM fusion system

will be presented.

5.1 Experimental Setup

The monomodal scores used in the experiments have

been provided by three experts: an SVM fusion of 9

speech prosodic features, a voice spectrum based

speaker recognition system and a facial recognition

expert based in the NMFFaces (Tefas et al., 2005)

algorithm.

In the prosody based recognition system a 9

prosodic feature vector was extracted for each

conversation side (Wolf, 1972). The system was

tested with 1 conversation-side, using the k-Nearest

Neighbour method. The prosodic vectors have been

fused by means of a SVM classificatory system with

RBF kernel to obtain a single monomodal score.

The spectrum based speaker recognition system

was a 32-component GMM system with diagonal

covariance matrices; 20 Frequency Filtering

parameters were generated (Nadeu et al., 1996), and

20 corresponding delta and acceleration coefficients

were included. The UBM was trained with 116

conversations.

The face recognition expert is based in the

NMFFaces algorithm (Tefas et al., 2005). Non-

negative matrix factorization is used in Tefas et al.

work to yield sparse representation of localized

features to represent the constituent facial parts over

the face images.

Prosodic and spectrum scores have been obtained

form speech records of the Switchboard-I database

(Godfrey et al., 1990) and the face scores have been

obtained from still images of the XM2VTS database

(Lüttin et Maître, 1998). The Switchboard-I is a

collection of 2,430 two-sided telephone

conversations among 543 speakers from the United

States. XM2VTS database is a multimodal database

consisting in face images, video sequences and

speech recordings of 295 subjects. A chimerical

database has been created by the combination of the

three expert scores. A total of 5,000 score vectors

have been generated for the training of the models

and 46,500 score vectors has been used in the test

phase.

5.2 Results

In the experiments, several normalization techniques

have been applied upon the monomodal scores.

Later, these scores have been fused by means of a

SVM system. The normalization methods are that

presented in previous sections: Min-Max (MM), Z-

Scores (ZS), a tanh based technique (TANH),

histogram equalization to the best monomodal

system (HEQ), and Bi-Gaussian equalization

(BGEQ).

To compare the effect of each normalization

method upon the SVM fusion system, an RBF kernel

based configuration has been tested. Concretely, for

the RBF kernel different values of the Gaussian

variance σ have been tested: 1/3, 1, and 3.

Furthermore, the regularization parameter C has

been set to 10, 100, and 200.

The minimum percentages of error provided by

the SVM verification system and the equal error rate

(EER) obtained by each normalization technique are

respectively presented in tables 1 and 2 for each

combination of the SVM parameters.

BGEQ obtains the best results and the rest of the

techniques obtain results with a difference of, at

least, a 10.51 % with respect to the best result.

Furthermore, the EER obtained by BGEQ is a 5.40

% better than that obtained by the non equalization

techniques. Concretely, Min-Max, the most used

normalization technique in SVM systems, is

outperformed by Bi-Gaussian equalization with a

relative error improvement of a 22.19 %.

The minimum results obtained with the

equalization techniques are from a 0.533 % to a

0.643 % while the best result obtained by the Min-

Max normalization is of a 0.826 %. In the same

way, the EER obtained by the equalization

techniques are from a 0.667 % to a 0.750 % and the

best result obtained by MM is a 0.815 %. That is, in

these experiments, the selection of an adequate

normalization method has been more decisive for

obtaining the best results than the choice of the

characteristics of the SVM system.

SECRYPT 2007 - International Conference on Security and Cryptography

Table 1: Multimodal results (minimum error).

C MM ZS TANH HEQ

BGE

1/3 10 0.854 0.632 0.619 0.613 0.600

100 0.729 0.791 0.632 0.611 0.611

200 0.714 0.830 0.613 0.617 0.641

1 10 0.940 0.615 0.729 0.622 0.587

100 0.849 0.617 0.652 0.611 0.533

200 0.826 0.589 0.660 0.602 0.540

3 10 0.976 0.628 0.770 0.643 0.611

100 0.946 0.742 0.710 0.613 0.602

200 0.905 0.754 0.703 0.617 0.578

Table 2: Multimodal results (EER).

C MM ZS TANH HEQ BGEQ

1/3 10 0.946 0.822 0.720 0.684 0.686

100 0.841 1.179 0.714 0.679 0.739

200 0.815 1.114 0.703 0.690 0.750

1 10 1.065 0.709 0.839 0.709 0.697

100 0.940 0.852 0.756 0.679 0.667

200 0.875 0.882 0.720 0.679 0.673

3 10 1.090 0.720 0.916 0.738 0.703

100 1.071 0.809 0.834 0.697 0.703

200 1.065 0.798 0.804 0.701 0.697

In figure 2, the DET curve for the comparison of the

normalization methods is shown.

Figure 2: DET curve for RBF kernel SVM.

For all the range of FAR and FRR, the best

results are obtained by HEQ and BGEQ that

outperforms the conventional normalizations for all

the FAR and FRR values. TANH obtains better

results than MM normalization and ZS

normalization only obtains similar results to TANH

for FAR lesser than 0.4 % due to the range of values

of the scores is not controlled by the Z-Score

normalization and this can produce unexpected

results.

6 CONCLUSIONS

Support Vector Machines fusion systems usually

make use of a Min-Max technique for the

normalization of the features or the scores. In this

work, several normalization methods have been

applied upon a multimodal score SVM fusion

system with RBF kernel.

The results obtained by the SVM system with the

MM normalization are improved by means of the

normalization of the scores with TANH

normalization and the equalization techniques.

Histogram equalization and Bi-Gaussian

equalization obtain the best results; concretely, Bi-

Gaussian equalization obtains a relative error

improvement of a 22.19 % with respect to MM

normalization and outperforms the normalization

techniques for all values of FAR and FRR.

In resume, in these experiments, the selection of

an adequate normalization method has been more

decisive for obtaining the best results than the choice

of the characteristics of the SVM system, as the

parameters of the kernel.

ACKNOWLEDGEMENTS

We want to thank Ms. Mireia Farrús for her help in

this work and Dr. A. Tefas who has provided us of

face recognition results.

REFERENCES

Bolle, R. M., Connell, J. H., Pankanti, S., Ratha, N. K.,

and Senior, A. W., 2004. Guide to Biometrics,

Springer-Verlag New York, Inc.

Jain, A. K., Nandakumar, K., and Ross, A., 2005. Score

normalization in multimodal biometric systems.

Pattern Recognition, vol. 38, no. 12, pp. 2270-2285.

Cristianini, N., and Shawe-Taylor, J., 2000. An

introduction to support vector machines (and other

kernel-based learning methods), Cambridge

University Press.

Wan, V., and Renals, S., 2005. Speaker verification using

sequence discriminant support vector machines. IEEE

Trans. on Speech and Audio Processing, 13:203-210.

Farrús, M., Garde, A., Ejarque, P., Luque, J., and

Hernando, J., 2006. On the Fusion of Prosody, Voice

Spectrum and Face Features for Multimodal Person

ON THE EFFECT OF SCORE EQUALIZATION IN SVM MULTIMODAL BIOMETRIC SYSTEMS

Verification. Proc. of Interspeech 2006, Pittsburgh,

USA.

Ejarque, P., Garde, A., Anguita, J., and Hernando, J.,

2007. On the use of genuine-impostor statistical

information for score fusion in multimodal biometrics.

Annals of Telecommunication, Multimodal Biometrics,

vol 62, nº 1-2.

Wolf, J. J., 1972. Efficient acoustic parameters for speaker

recognition. Journal of the Acoustical Society of

America, vol. 51, pp. 2044-2056.

Nadeu, C., Mariño, J. B., Hernando, J., and Nogueiras, A.,

1996. Frequency and time-filtering of filter-bank

energies for HMM speech recognition. ICSLP, pp.

430-433, Philadelphia, USA.

Tefas, A., Zafeiriou, S., and Pitas, I., 2005. Discriminant

NMFfaces for frontal face verification. Proc. of IEEE

International Workshop on Machine Learning for

Signal Processing (MLSP 2005), Mystic, Connecticut,

September 28-30.

Jain, A., 1986. Fundamentals of Digital Image Processing,

Prentice-Hall, pp 241 - 243.

Balchandran, R., and Mammone, R., 1998. Non

parametric estimation and correction of non-linear

distortion in speech systems. Proc. IEEE Int. Conf.

Acoust. Speech Signal Proc.

Godfrey, J. J., Holliman, E. C., and McDaniel, J., 1990.

Switchboard: Telephone speech corpus for research

and development. ICASSP.

Lüttin, J., and Maître, G., 1998. Evaluation Protocol for

the Extended M2VTS Database (XM2VTSDB).

IDIAP Communication 98-05, Martigny, Switzerland.

SECRYPT 2007 - International Conference on Security and Cryptography