DC MOTOR USING MULTI ACTIVATION WAVELET
NETWORK (MAWN) AS AN ALTERNATIVE TO
A PD CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
Walid Emar, Noora Khalaf, Maher Dababneh and Waleed Johar
Al-Isra Private University, Amman Jordan
Key words: Robotics, Control System, Wavelet Network, DC motor controller
.
Abstract: In this paper, a robust MAWN is proposed. An application that constructs Wavelet Network as an
alternative to a PD controller in the robotics control system with DC motor is fully investigated.
Experimental results not only show that the target performance can be achieved by the proposed Wavelet
Network, but also it outperforms the conventional PD controller. An literature survey was conducted to shed
some light into this research field shows a sparsity of work addressing this concept, and this what stimulated
the idea of this work.
1 INTRODUCTION
The design of intelligent, autonomous machines to
perform tasks that are dull, repetitive, hazardous, or
that require skill, strength, or dexterity beyond the
capability of humans is the ultimate goal of robotics
research. Examples of such tasks include
manufacturing, excavation, construction, undersea,
space, and planetary exploration, toxic waste
cleanup, and robotic assisted surgery. Robotics
research is highly interdisciplinary requiring the
integration of control theory with mechanics,
electronics, artificial intelligence and sensor
technology (Xiao, 2001).
The ever increasing technological demands of
to
day, call for very complex systems, which in turn
require highly sophisticated controllers to ensure
that high performance can be achieved and
maintained under adverse conditions. There are
needs in the control of these complex systems,
which cannot be met by conventional approaches to
control. For instance, there is a significant need to
achieve higher degrees of autonomous operation for
robotic systems, spacecraft, manufacturing systems,
automotive systems, underwater and land vehicles,
and others. To achieve such highly autonomous
behavior for complex systems, one can enhance
today's control methods using intelligent control
systems and techniques (Feitosa et al., 2000).
Intelligent control methodologies are being
appl
ied to robotics and automation, communications,
manufacturing, traffic control. To mention few
application areas: neural networks, fuzzy control,
genetic algorithms, planning systems, expert
systems, and hybrid systems are all related areas.
The term "intelligent control" has come to mean,
particularly to those outside the control area, some
form of control using fuzzy and/or neural network
methodologies (Sgarbiy et al., 1997).
Neural networks have been applied very
success
fully in the identification and control of
dynamic systems. The universal approximation
capabilities of the multilayer perceptron (the
backpropogation algorithm) make it a popular
choice for modeling nonlinear systems and for
implementing general-purpose nonlinear controllers
(Calise and Rysdyk, 1996). The combination of soft
computing and wavelet theory has lead to a number
of new techniques: MAWN, wavenets, and fuzzy-
wavelet (Yao, 1999).
It is difficult to model the environment to
p
rovide the controller with the relevant data and
program actions for all possible situations. Hence,
controllers with abilities to learn and to adapt are
needed to solve this problem. Soft computing
provides an attractive venue to deal with these
situations. Soft computing methods are based on
biological systems and can provide the following
features: generalization, adaptation and learning. As
more is realized about the use and properties of soft
computing methods, the development of controller is
341351
Emar W., Khalaf N., Dababneh M. and Johar W. (2007).
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD CONTROLLER IN THE ROBOTICS
CONTROL SYSTEM.
In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 341-347
DOI: 10.5220/0002131603410347
Copyright
c
 SciTePress

shifting towards using soft computing (Gu and Hu,
2002).
In this paper a robust Multi Activation Function
Wavelet Network Wavelet (MAFWN) is used as a
controller analogous to a PD controller in the control
of a robotic arm and a payload system with a DC
motor that is required for conducting a pick and
place operation to achieve the required performance.
2 THE MULTI MAFWN
An application of multi wavelet filters to neural
networks is investigated in this paper. This new
technique called MAFWN. It is an interesting
alternative to wavelet networks that absorbs the
advantage of high resolution of wavelets and the
advantages of learning feed-forward neural
networks.
The MAFWN is very similar to wavelet Network
(WN) but, has some important differences, whereas
wavelets have an associated scaling function φ(t)
and wavelet function ψ(t). MAWN has multi scaling
φ1(t), φ2(t) … φn(t), and multi wavelet functions
ψ1(t), ψ2(t) … ψn(t). However, Two AFWN
(TAFWN) has two scaling functions φ1(t), φ2(t) and
two wavelet functions ψ1(t), ψ2(t). Subsequently,
there are two scaling filters and two wavelet filters
for the case of TAFWN, and this will be considered
as a case study for this research.
3 WAVELET NETWORK
ALGORITHM
The two activation function wavelet network
(TAFWN) architecture approximates any desired
signal by generalizing a linear combination of
two set of daughter wavelets and
)(ty
)(
,,1
th
ba
)(
,,2
t
h
ba
,
where the daughter wavelets
)(
,,1
t
h
ba
and
)(
,,2
t
h
ba
are generated by dilation, a , and
translation, , from two mother wavelets
b
)()(
21
τ
τ
handh
, where
a
bt −
=
τ
.
)()(
1
,,1
a
bt
hth
ba
−
=
(1)
)()(
2
,,2
a
bt
hth
ba
−
=
(2)
Where:
a
: Dilation factor, with
a
> 0.
b
: Translation factor.
:
t
Signal time interval
The network architecture is shown in figure (1).
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
11
11
11
a
bt
h
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
21
21
21
a
bt
h
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
12
12
12
a
bt
h
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
22
22
22
a
bt
h
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
k
k
k
a
bt
h
1
1
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
k
k
k
a
bt
h
2
2
2
X
(
t
)
)(ty
∧
W
11
W
12
W
22
W
21
W
1k
W
2k
Figure 1: Structure of TAFWN.
A TAFWN is a 3-layers feed forward neural
network. First the TAFWN parameters, dilation a's,
translation b's, and weight w's should be initialized,
and the desired sets of data, the input signal x(t), the
desired output (target) y(t), the number of scaling
functions p (p=2 in this work) and the number of
wavelons k are given. The approximated signal of
the network can be represented by equation:
)(
ˆ
ty
TAFWN is trained by the gradient descent
algorithms like least mean squares (LMS) to
minimize the mean-squared error. During learning,
the parameters of the network are optimized.
∑∑
×=
==
k
i
ij
b
ij
aij
p
j
thwtxty
1
,
,
,
,
1
)()()(
ˆ
(3)
Where: x(t) is the input signal.
ij
w
,
is the weight coefficients between hidden
and output layers.
j=1,2,…, p. p=2: a number of scaling functions.
i=1,2,…, k. k is a number of wavelons.
ij
b
ij
a
h
,
,
,
is a two set of daughter wavelets generated
from two mother wavelets
)(),(
21
thth
as in
equations (1) and (2) respectively.
The TAFWN parameters
i
,
j
w
,
ij
a
,
, and
i
can
be optimized in the LMS algorithm by minimizing a
cost function or the energy function,
j
b
,
E
, over all
function interval. The energy function is defined by
equations (4) and (5), is the desired output
(target) and is the actual output signal of
TAFWN.
)(ty
)(
ˆ
ty
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
342
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
352

∑
=
=
T
t
teE
1
2
)(
2
1
(4)
∑
=
−=
T
t
tytyE
1
2
))(
ˆ
)((
2
1
(5)
Where,
T
is the total interval of function,
)(
t
y
is the desired output (target) and is the actual
output signal of WN.
)(
ˆ
ty
To minimize then the method of steepest
descent is used, which requires the gradients
E
ij
w
E
,
∂
∂
,
ij
a
E
,
∂
∂
, and
ij
b
E
,
∂
∂
for updating the incremental changes to each
particular parameter
ij
w
,
,
ij
a
,
, and
ij
b
,
,
respectively. The gradients of are given as
follows:
E
() ( ) ()
txhte
w
E
T
t
ij
τ
∑
−=
∂
∂
=1
,
(6)
() ()
()
ij
b
h
ij
T
t
ij
wtxte
b
E
,
,
1
,
∂
∂
=
∑
−=
∂
∂
τ
(7)
ij
T
t
ij
ij
ij
b
E
b
h
wtxte
a
E
,
1
,
,
,
)(
)()(
∂
∂
=
∑
∂
∂
−
=
∂
∂
=
τ
τ
τ
(8)
ij
ij
a
bt
,
,
−
=
τ
(9)
Derivatives of the various wavelet filters with
respect to its translation
ij
b
h
,
)(
∂
∂
τ
, are given in (Oussar
et al., 1996).
The incremental changes of each coefficient are
simply the negative of their gradients.
w
E
w
∂
∂
−=Δ
(10)
b
E
b
∂
∂
−=Δ
(11)
a
E
a
∂
∂
−=Δ
(12)
Thus, each coefficient , and of the
network is updated in accordance with the rule
given:
w
b
a
w
t
w
t
w
w
Δ+=+
μ
)()1(
(13)
b
t
b
t
b
b
Δ+
=
+
μ
)()1(
(14)
atata
a
Δ+
=
+
μ
)()1(
(15)
Where,
μ
is the fixed learning rate parameter
(Oussar et al., 1996).
2. Set: the number of trainings, iter =0, the
incremental changes of each coefficient,
0),,(
=
Δ
Δ
Δ
baw
, and the initial square error,
5.0
=
ite
r
E
3. Calculate the approximated signal of the
network using equation (3).
)(
ˆ
ty
4. Calculate the gradients of each coefficient
using equations (6), (7), (8) and calculate the
coefficients incremental changes which are the
negative of their gradients.
5. Choose a constant
μ
, such that 0.01 ≤
μ
≤1
and calculate the new coefficients ,
1+iter
w
1+ite
r
b
, and
1+iter
a
of the network in accordance
with the rules given in equations (13), (14) and (15).
6. Calculate the square error
1+ite
r
E
using
equation (5).
If
1+ite
r
E
is small enough, then the training is
good and the run of the algorithm is stopped.
Otherwise, set iter = iter + 1 and go to (3) again.
At every iteration, the network parameters are
modified using the gradient descent algorithm that
will result in minimizing the parameter E.
The training algorithm of the proposed TAFWN
consists of the following six steps:
1. Initialize TAFWN parameters, dilation a's,
translation b's, and weight w's, p=2, two mother
wavelets filters
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
i
a
i
bt
i
a
i
bt
hh
21
,
,
the desired sets of data, the input signal x(t), the
desired output (target) y(t), and the number of
wavelons k are given.
4 MAWN FOR CONTROLLING A
ROBOTIC ARM
An example-control of a robotic arm and a payload
system with a DC motor- is given in this paper to
illustrate the use of the proposed MAWN as a PD
controller and its performance.
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD
CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
343
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD
CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
353

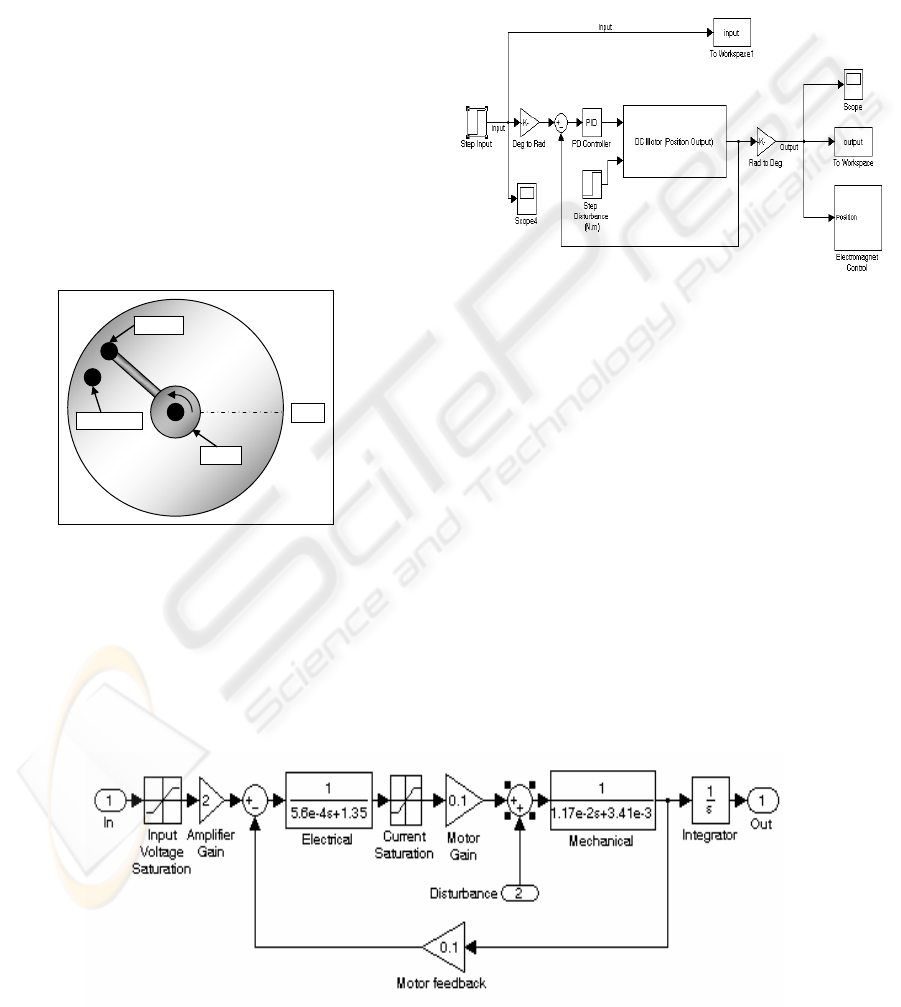
4.1 Robotic Arm Properties
The Robotic arm is depicted in Figure (2). It is
composed of a rigid beam which is connected to a
motor shaft to create a robotic system conducting a
pick and place operation. A solid disk is attached to
the end of the beam through a magnetic device (e.g.,
a solenoid). If the magnet is on, the disk will stick to
the beam, and when the magnet is turned off, the
disk is released. The objective of the robotic arm is
to drop the disk into a hole as fast as possible. The
hole is 1 inch (25.4 mm) below the disk as shown in
figure (3) (Oussar and Dreyfus, 1996). The robot
arm is required to move in one direction only, from
the initial position. Also, the hole location may be
anywhere within an angular range of 20° to 180°
from the initial position. It is in the angular position
of 150° for the sake of this example. The idea of this
control system is to move a metal object attached to
a robot arm by an electromagnet from position 0° to
the angular position 150° with a specified overshoot
and minimum overall time.
Star
Motor
Pa
y
l
o
a
d
Dro
p
off tar
g
e
t
Figure 2: Control of a robotic arm and payload.
A system simulink model of the system is shown
in figure (4) and the simulated DC Motor is
portrayed in Figure (5). This figure represents a
simple PD controller model with proportional gain
of 15 and derivative gain of 2.1. In the
Electromagnet Control block, drop-off payload
location and the time delay (in seconds) to turn the
magnet off after reaching the target parameters is
adjusted to 150° and 0.8 sec, respectively. So, the
"Drop position angle" is the angle where the
electromagnets turn off, thereby, dropping the
payload." However, start to wait for drop position at
time" refers to the time where the position triggers
starts to wait for the position specified by "Drop
position angle." An overall time response for the
system with PD controller is shown in Figure (6).
Figure 3: The robotic arm system simulink model.
4.2 TAFWN as PD Controller
Now, the PD controller shown in figure (5) is
replaced with the proposed TAFWN structure.
TAFWN of 40 [Morlet, Rasp2] filters and fixed
learning rate of 0.1 is trained first with the desired
input-output data set shown in figure (6- a and b).
Figure (7) however, shows the training performance
of the network.
After training to MSE value less than e-005, the
trained TAFWN is employed to control the robotic
arm system, the system simulink model with
TAFWN controller is shown in figure (8). It is clear
from the above results that the TAFWN is proved to
be a PD controller, and its position response per time
Figure 4: The simulated DC Motor.
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
344
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
354

Time (sec)
Figure 5: Position response (degree) per time (sec) with PD controller.
Time (sec)
(a) the input to TAFWN
Time (sec)
(b) the desired output of TAFWN
Figure 6: The desired input-output data set.
Figure 7: Mean-Square Error per learning iteration.
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD
CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
345
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD
CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
355

Figure 8: Robotic arm system simulink model with TAFWN controller.
Position (deg)
Time (sec)
Figure 9: Position response (degree) per time (sec) with TAFWN controller.
is illustrated in figure (9). As it is shown at the
specified time (0.8 sec), the angular position angle
150° and so the metal object attached to the robot
arm is gotten to be in the "Drop position angle"
(150°) at time (0.8 sec). Hence there is no significant
difference between the position responses for both
PD and TAFWN controllers.
5 CONCLUSIONS
In this paper, an advanced wavelet network, called
Two Activation Function Wavelet Network is
presented as an interesting alternative to wavelet
networks. This technique absorbs the advantage of
high resolution of wavelets and the advantages of
learning and feed-forward of neural networks. The
algorithm of function identification is designed and
implemented using Matlab 6.5 tool.
The Two Activation Function Wavelet Network
(TAFWN) structure is implemented and several
examples are carried out to verify this
implementation. It can be concluded that this
structure achieves an approximation assuming
reasonable choice of the number of wavelons and
mother wavelet basis functions. The Two Activation
Function Wavelet Network is proved to be a
controller analogous to PD controller. After the off-
line training of the TAFWN controller, it shows the
ability to get the specified position response exactly
at the specified time when it's embedded in the
control system. No significant difference between
the position responses for both PD and the proposed
TAFWN controllers, indicating further the validity
of the idea of this research.
REFERENCES
Panrong Xiao, "Image Compression by Wavelet
Transform", A Thesis presented to the faculty of
Computer and Information Sciences East Tennessee
State University, August 2001.
R. Q. Feitosa
1,2
, M. M. B. Vellasco
1,2
, D. T. Oliveira
1
, D.
V. Andrade
1
, and S. A. R. S. Maffra
1
, "Facial
Expression Classification Using RBF AND Back-
Propagation Neural Networks", Catholic University of
Rio de Janeiro, Brazil Department of Electric
Engineering, State University of Rio de Janeiro, Brazil
Department of Computer Engineering, 2000.
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
346
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
356

M. Sgarbiy, V. Colla, and L.M. Reyneri , "A Comparison
Between Weighted Radial Basis Functions and
Wavelet Networks", Department of Electronic,
University of Torino, C.so Duca degli Abruzzi 24,
10129 Torino, Italy, 1997.
Anthony J. Calise, and Rolf T. Rysdyk, "Nonlinear
Adaptive Flight Control using Neural Networks",
Georgia Institute of Technology School of Aerospace
Engineering Atlanta, GA, 30332, 1996.
Xin Yao, Senior member, IEEE, "Evolving Artificial
Neural Networks", Proceedings of the IEEE, Vol. 87,
No. 9, September, 1999.
Dongbing Gu and Huosheng Hu, "Neural Predictive
Control for a Car-like Mobile Robot", Department of
Computer Science, University of Essex Wivenhoe
Park, Colchester CO4 3SQ, UK, International Journal
of Robotics and Autonomous Systems, Vol. 39, No. 2-
3, May, 2002.
Y. Oussar, I. Rivals, L. Personnaz, and G. Dreyfus,
"Training Wavelet Networks for Nonlinear Dynamic
Input-Output Modeling", Laboratory of Electronic
Superior School of Physical and Chemistry Industrial
10, rue Vauquelin F - 75231 Paris Cedex 05, France,
1996.
Yacine Oussar, Gerard Dreyfus, "Initialization by
Selection for Wavelet Network Training", Laboratory
of Electronic Superior School of Physical and
Chemistry Industrial 10, rue Vauquelin F - 75231
Paris Cedex 05, France, 1996.
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD
CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
347
DC MOTOR USING MULTI ACTIVATION WAVELET NETWORK (MAWN) AS AN ALTERNATIVE TO A PD
CONTROLLER IN THE ROBOTICS CONTROL SYSTEM
357