
SPECTRUM WEIGHTED HRTF BASED SOUND LOCALIZATION
Sergio Cavaliere and Pietro Santangelo
Dipartimento di Scienze Fisiche, Universit
´
a Federico II, Naples, Italy
Keywords:
C.A.S.A, Binaural Sound Localization, HRTF, Robot Sensing Systems.
Abstract:
In the framework of humanoid robotics it’s of great importance studying and developing computational tech-
niques that enrich robot perception and its interaction with the surrounding environment. The most important
cues for the estimation of sound source azimuth are interaural phase differences (IPD), interaural time differ-
ences (ITD) and interaural level differences (ILD) between the binaural signals. In this paper we present a
method for the recognition of the direction of a sound located on the azimuthal plane (i.e. the plane containing
the interaural axis). The proposed method is based on a spectrum weighted comparison between ILD’s and
IPD’s extracted from microphones located at the ears and a set of stored cues; these cues where previously
measured and stored in a database in the form of a Data Lookup Table. While the direct lookup in the table
of the stored cues suffers from the presence of both ambient noise and reverberation, as usual in real envi-
ronments, the proposed method, exploiting the overall shape of the actual frequency spectrum of the signal,
both its phase and modulus, reduces dramatically errors in the localization. In the paper we give also the
experimental evidence that such method improves greatly the usual HRTF based identification methods.
1 INTRODUCTION
In humanoid robotics applications main sensory ap-
paratus are vision and hearing. While vision un-
doubtedly provides main spatial details of surround-
ing environment, it is the sense of hearing that en-
riches perception of new and invaluable information:
it gives, for example, precious information due to sud-
den changes in the scene. In few words it is for com-
munications purposes that the ability to produce and
localize sounds becomes mandatory.
The term CASA (Computational Auditory Scene
Analysis) denotes the group of techniques that try to
mimic the behaviour of human auditory system, or at
least some of its features which appear to be more rel-
evant for the identification of sound sources. Binau-
ral Localization denotes the task of estimating sound
source position based on the analysis of signals col-
lected at the ears; the role played by the head is es-
sentially that of filtering incoming sounds in order to
feed all necessary information to the brain so that both
azimuth and height localization of sound source posi-
tion may take place.
The modifications on the incoming signal as col-
lected at the ears can be successfully modeled by a
linear filter whose transfer function is called Head Re-
lated Transfer Function (HRTF); binaural information
(cues), mainly phase and intensity differences, can be
obtained from a measured set of HRTFs, yielding az-
imuth data lookup models(Algazi, D uda, Thompson
and Avendano 2001).
1.1 Earlier Works
In the last years several computational methods have
been developed for the extraction of sound source az-
imuth angles from binaural signals.
Some of them are based on the coincidence model
proposed by Jeffress in 1948 (see (Joris, Smith and
Yin, 1998)). This is a model of the neural system
where nerve impulses from each of the two ears prop-
agate along delay lines in opposite directions. At the
position where the impulse coincide a nerve cell is ex-
cited, effectively transforming time information into
169
Cavaliere S. and Santangelo P. (2007).
SPECTRUM WEIGHTED HRTF BASED SOUND LOCALIZATION.
In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 165-170
DOI: 10.5220/0002136001650170
Copyright
c
SciTePress

spatial information. A method to evaluate this ITD
delay over time is that of computing a running short-
time cross correlation between signals collected at the
ears (Knapp and Carter (1976)). In this method, if sig-
nals are previously filtered, we can successfully take
into account the actual spectrum of the incoming sig-
nal in order to reduce at some extent the effect of
noise and reverberation. However the failure rate of
the identification methods based on the Generalized
Cross Correlation, when used at practical values of
SNR results relatively high, thus preventing in many
cases real time applications.
Another method, proposed in (Viste, 2004) and
(Evangelista and Viste, 2004) is based on joint evalu-
ation of the ITD and ILD cues obtained by means of a
running Short Time Fourier Transform (STFT); here
the ILDs are used in order to resolve the ITD ambigu-
ity due, as is well known, to phase ambiguity: in this
method, gross identification is performed by means
of ILD, while ITD evaluation is used to improve az-
imuth estimate. This method, since it performs the
evaluation at each frequency bin, is suitable to take
into account bin per bin weights as in our proposal.
A third class consists in methods based on a very
strict sensory fusion as in Hokuno (see (Nakadai,
Okuno and Kitano 2001)). These also may take ad-
vantage of an improved calculation based on acousti-
cal cues, as in our proposal.
The last class to be taken into account is based
on the use of a neural network trained with cues ex-
tracted from binaural signals as discussed e.g. in (Irie
(1995)); even in this case the proposed method of
weighting cues may be invaluable.
Our proposed implementation may thus be em-
bodied in existent architectures, improving their per-
formance and robustness.
-20
-80
20
80
-20
-60
60
-80
20
80
-20
-60
60
Figure 1: HRIR measured for both left and right sides.
1.2 Contribution
The method here exposed belongs to the second class
of methods summarized in the previous section; his
starting point is (as in (Viste, 2004) and (Evangelista
and Viste, 2004)) the measure of the set of HRTFs
on a grid of positions corresponding to several dif-
ferent azimuth angles (in fig.1 we show their time
domain counterpart: the Head Related Impulse Re-
sponse HRIR); from these transfer functions we ob-
tain the ILD
h
(θ, ω) and the IPD
h
(θ, ω), functions of
azimuth θ and frequency ω, evaluated at discrete an-
gular positions and frequencies.
The IPD
m
(ω
k
) and ILD
m
(ω
k
) measured
1
time by
time from an observed signal pair at the robot ears us-
ing Short Time Fourier Transform (STFT), are com-
pared against the HRTF data set in order to obtain an
estimate of the source azimuth: the position yielding
minimum deviation from the stored table is selected
as true azimuth. This is referred to as HRTF Data
Lookup: azimuth estimates by use of this techniques
are based on ILD and IPD separately.
In our proposal estimate of the angle is obtained
by minimizing the error, properly weighted in fre-
quency (as shown in section 3), made by comparing
these cues with the ILD
h
(θ, ω) and IPD
h
(θ, ω) func-
tions stored in the Data Lookup Table; the effect of
weighting is clearly seen in fig.2 where the straight
deviation from a curve in the table at a specific az-
imuth is shown in the upper part of the figure. In
the lower part the same deviation is weighted by an
evaluation of the signal spectrum: only the bins in
the spectrum where signals is larger and than exhibit
higher SNR are taken into account.
The signal used in the figure shows narrowband
contents limited to a small part of the frequency axis.
The comparison is made all over the frequency
axis or, more successfully, in selected frequency
bands; in fact on the ground of Duplex Theory
((Blauert (1997))) the ITD and ILD cues are sig-
nificant in different and complementary frequency
ranges, mainly low range for ITD and high range for
ILD.
The position in the azimuth grid corresponding to
a minimum in the weighted error function is chosen
as the best estimate of sound source position,(see fig-
ure 3, where the successful estimate in weighted case
is -24, while unweighted method shows a clear error,
estimating -6 as azimuth sound position). Also, based
on the evaluation on the whole grid, a measure of the
reliability of the measurement may be given in form
of error ratio between neighbor azimuth positions.
1
The subscript h refers to the HRTF cue while subscript
m refers to the measured cue
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
170

Figure 2: Unweighted and weighted error as function of the
frequency for an arbitrary azimuth.
It is seen from the figure that the weighting
method, grants higher error margins and therefore ex-
hibits greater reliability and robustness.
Figure 3: Weighting the Error Function clearly sharpens its
minimum peak.
2 CUE ESTIMATION
2.1 ILD
The ILD cue is mostly due to sound shadowing by
the head, an effect which is highly frequency depen-
dent; outer structure of the ears (pinnae) also affect
this dependence. At low frequencies where wave-
length is comparable to the size of the head, shad-
owing may be neglected, while at higher frequencies
it becomes more consistent, delivering level differ-
ences up to tens dB. Theoretical formula for this de-
pendence is very complex (see (Nakadai, Matsuura,
Okuno and Kitano, 2003) for a version of it) while
it’s not hard to extract it from the binaural signals: if
p
r
and p
l
are the sound pressures at the ears, ILD in
dB is given by:
ILD = L
(r)
p
− L
(l)
p
= 10
log
10
p
2
r
− log
10
p
2
l
(1)
where the signal spectra are evaluated by means of
DFT, expression of the ILD for each frequency bin
simply becomes the ratio in dB of the different bin
amplitudes of right to left signals:
ILD[k] = 20log
10
Y
r
[k]
Y
l
[k]
2.2 ITD, IPD and Unwrap Problems
The difference in the path that a sound wave covers to
reach the two ears results in a time and phase differ-
ence between the waveforms collected at the ears. If
we consider a spherical head with radius r =
d
2
, where
d is interaural distance, neglecting the shadowing ef-
fect of the head and under the hypothesis that the dis-
tance R of the sound source is much greater than d,
time difference is given by :
∆T =
∆ρ
c
≃
2rsinθ
c
. (2)
where ∆ρ is the difference of path between the two
incoming waves and c is the speed of sound. If X
r
[k]
and X
l
[k] are the binaural signal spectra, the resulting
estimate of ITD for each bin is:
ITD[k] =
−IPD[k] ·L
2π·k
(3)
where IPD is given by
IPD[k] = arg
X
r
[k]
X
l
[k]
(4)
Here the usual problem of proper unwrapping, i.e.
correct choice of the 2πn offset to be added at wrap-
ping points, is met: this offset in fact depends on both
frequency and sound source angular position and can-
not be defined a priori; this problem furthermore is
increased by uncorrelated noise between the two sig-
nals.
We overcome this problem avoiding the calcula-
tion of ITD and simply using the rough wrapped IPD
cues. Actually in this way the comparison is made be-
tween the general shape of the phase (and its deriva-
tive) for each segment where this function may be
SPECTRUM WEIGHTED HRTF BASED SOUND LOCALIZATION
171

Figure 4: Close lookup of IPD function for both HRTF and
measured cues.
considered as continuous in frequency; this is clearly
shown in fig.4 where we show a close look-up of the
straight phase difference from the true azimuth in the
reference table and, superimposed, the same differ-
ence from the measured signals: their apparent simili-
tude, resulting in low values of the difference between
the measured values and their stored counterpart is the
basis of this table lookup method.
In fig. 5 we show the histogram of the derivative
of the phase function computed as the difference from
sample to sample; out of range values, due to disconti-
nuity at wrapping frequencies are easily discarded by
means of a simple statistical rejection criterion (Chau-
venet), discarding samples more than, say, twice the
standard deviation.
The histogram is reported for different values of
the azimuth: we may clearly observe the peaks at se-
lected values of the phase derivative or group delay,
showing the existence of a ”main value” for the slope
of the phase curve at each specified azimuth (the mean
values in the histograms of fig.5).
The proposed method instead than relaying on a
guess of the right wrapping values, relies on a global
fit against the shape of the phase response; it actually
reveals to be extremely efficient, yielding the satisfac-
tory results reported later.
3 EXTRACTION OF THE
AZIMUTH ANGLES
After the measurement of the cues, at each position
in the azimuth grid for which HRTFs were computed,
we evaluate the weighted error function:
Figure 5: Histogram of point-by-point IPD derivative.
S
IPD
(θ
i
, ω
k
) =
q
(IPD
h
(θ
i
, ω
k
) − IPD
m
(ω))
2
·W(ω
k
)
(5)
Same formula holds for the calculation of
S
ILD
(θ
i
, ω
k
). The weight W is obtained from the bin-
aural spectra and has the purpose to give larger weight
to those bins in the spectrum where energy is concen-
trated and where SNR is higher; on the opposite side,
in frequency ranges where the signal has low energy,
the collected information is to be ascribed mostly to
noise and reverberation yielding therefore erroneous
and random information on the phase and amplitude
content (see fig.2).
This choice, on the ground of the above consider-
ation, may be regarded as a counterpart of the weight
used in the GCC method for the evaluation of time
differences. In the case of the determination of the
Cross Correlation in a generalized way, in order to
select bins carrying uncorrupted information we per-
form proper filtering, say PHAT, ROTH, SCOT or
others (see (Knapp and Carter (1976)) for detailed
discussion); in our case, where mostly phase of the
bins is used, proper selection is performed just by
scaling errors in the ILD and IPD by means of weight-
ing with the amplitude of the source signal: best eval-
uation of this amplitude is just the amplitude of the
received signal (see lower part of fig.2). In our ex-
periment we use successfully the following analytical
expression for W computed at discrete bins:
W[k] =
1
2
|X
r
[k]|
max
j
|X
r
[ j]|
+
|X
l
[k]|
max
j
|X
l
[ j]|
but different weighting laws perform as well.
The azimuth angle is the angle that minimizes the
norm of weighted errors for both parameters in the
following way:
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
172
θ
IPD
=
θ
j
: kS
IPD
(θ
j
, ω
k
)k = min
i
{
kS
IPD
(θ
i
, ω
k
)k
}
θ
ILD
=
θ
j
: kS
ILD
(θ
j
, ω
k
)k = min
i
{
kS
ILD
(θ
i
, ω
k
)k
}
4 EXPERIMENTS AND RESULTS
Experiments previously conducted by means of a
software simulator (for experimental and software
code detail see (Santangelo (2006))) using HRTF
from the CIPIC Database ((Algazi, D uda, Thomp-
son and Avendano 2001)) have been also performed
by means of a platform consisting of a robotic head
on a rotating table (shown in fig.6) and related au-
dio hardware. As sensors at the ears we used two
TCM110 electret condenser Tie-Clip microphones by
AV-JEFE. The signals where acquired by means of
the FirePod, a 24bit 96KHz firewire recording inter-
face by PreSonus.
Figure 6: The platform used for the experiments.
The transfer functions of the robotic head were ac-
quired in a noisy environment (up to 35dB SNR) with
a purposely developed software based on a swept sine
technique (as shown in (Berkout, de Vries and Boone,
1980), (Farina, 2000) and (Santangelo (2006))).
By means of the rotating table we swept the whole
range of positions of the head acquiring measure-
ments for the verification. Results of this measure-
ments are reported in fig. 7 and fig. 8 in the form of
histograms of the detected position for one hundred
test at each of the angular position of the complete
turn; the performance of the proposed algorithm may
be easily evaluated.
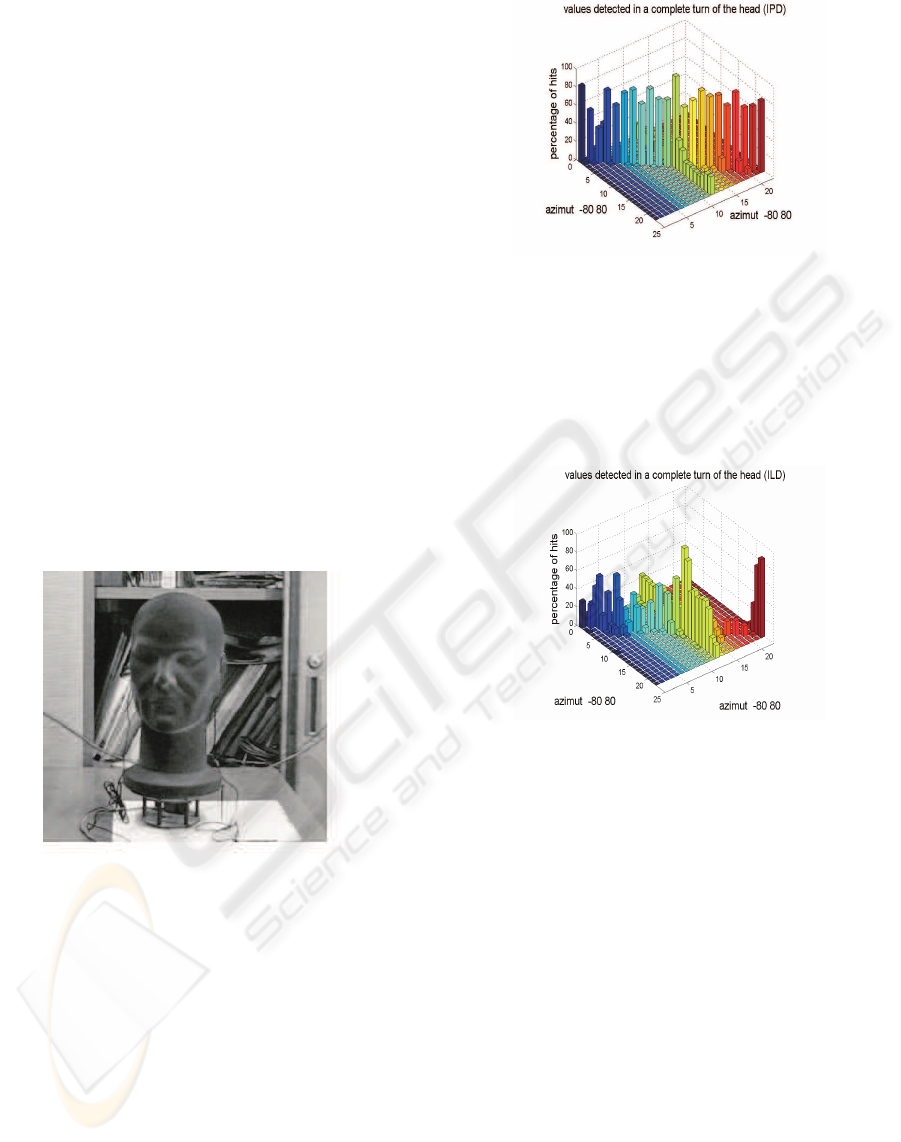
Figure 7: Hit rates for weighted IPD based localization
around all grid positions.
Figure 7 shows results in the evaluation of IPD
while the figure 8 uses ILD cues. In this latter case
results are less robust, especially at extreme positions,
where, as well known, angular resolution is poorer.
Figure 8: Hit rates for weighted ILD based localization
around all grid positions.
The histograms of both figures, show the azimuth
values proposed in a complete turn of the head (180).
These histograms normalized to 100, as far as regards
the bars related to the true positions taken during the
experiment (the positions on the -80 80 diagonal) pro-
vide also the probability of success in the identifica-
tion (hit rate); this figure in most cases is very close
to 100 percent; we must moreover take into account
the circumstance that information on angular position
taken by considering IPD only may be confirmed by
means of the evaluation based on ILD and finally in-
tegrated over time by means of a running evaluation,
based on STFT: the resulting figures appear therefore
to be very satisfactory.
Results, as expected, appear to be more precise at
positions close to zero (front positions) and provide
higher hit rates while using the IPD cue instead of
ILD. The experiments reported in the above figures
where conducted using 100 time slots for the duration
of 50ms each, taken from a collection of five differ-
SPECTRUM WEIGHTED HRTF BASED SOUND LOCALIZATION
173
ent kind of sounds: male voice, female voice, boys,
white noise and a telephone tone, thus providing both
wideband and narrowband features.
Figure 9: Localization of a narrowband signal. Results are
shown for weighted ILD (stars) weighted IPD (diamonds)
and unweighted IPD (crosses).
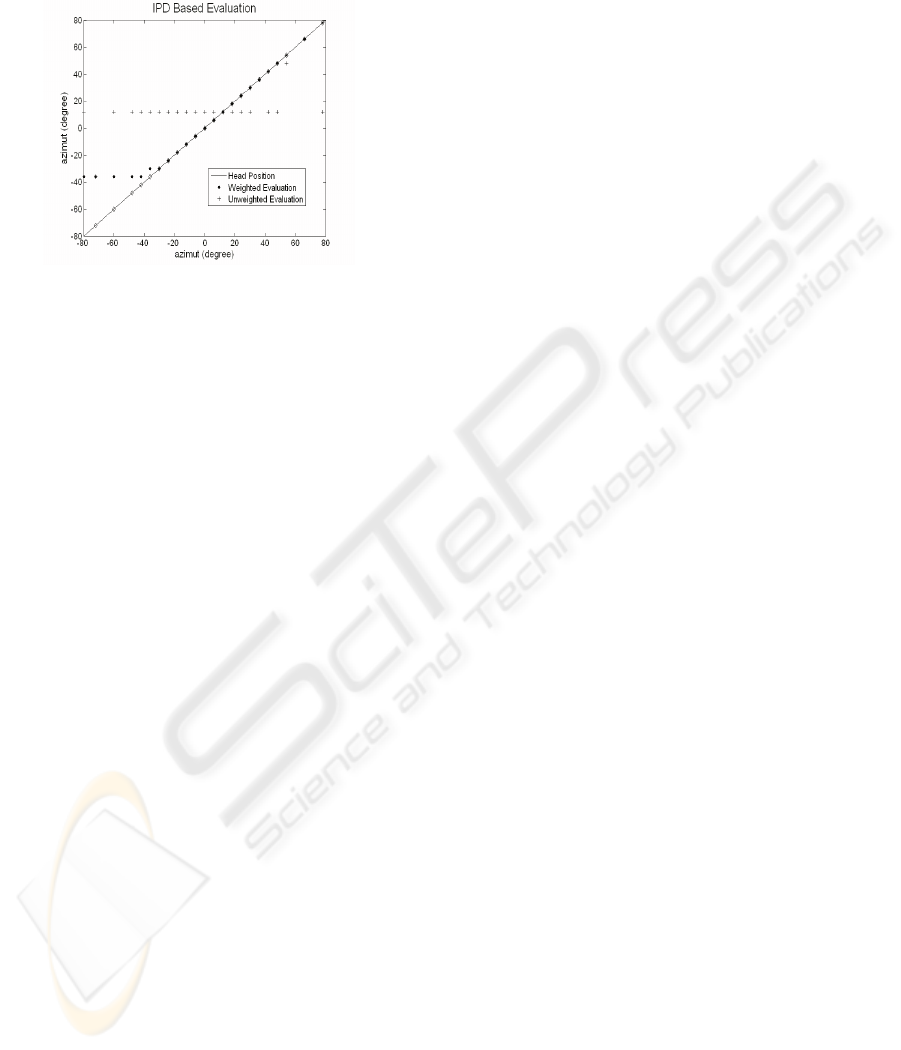
In fig. 9 finally we report results of a narrowband
sound localization obtained under the same noise and
reverberation conditions by means of the weighted
and non weighted table look up methds. It is clear
from the diagram that, for all azimuth positions the
proposed weighting outperforms the straight look-up
method which, while it works in a satisfactory way
in simulation by means for example of the CIPIC
database (Algazi, D uda, Thompson and Avendano
2001), actually delivers very poor results and high
miss rates in the real world conditions.
As expected and as clearly shown in this figure,
improvement in performance is greater in the case of
narrowband and monochromatic sounds. It is in these
cases that, using prevailingly information from bins
where the signal shows more energy, exhibiting there-
fore higher SNR, allows drastically improved perfor-
mance and provide the confidence that the proposed
method appear to be a good candidate for real world
performance.
5 CONCLUSIONS
The proposed method seems to outperform the basic
table lookup method of which it may be regarded as
an extension, compensating for noise and reverber-
ation in real world environments: in the paper we
reported the experimental evidence of this. For its
promising features the method was chosen for further
experiments on a real robot architecture (platform PI-
ONEER 3-DX8) on which we are porting the method
for real time operation together with an algorithm for
face recognition and identification in a multisensory
environment. On this we will report shortly.
REFERENCES
H.Viste (2004). Binaural Localization and Separation.
Ph.D. thesis Ecole Polytechnique Federale de Lausan-
nen. (EPFL), Switzerland.
G.Evangelista and H.Viste (2004). Binaural Localization.
In Proceedings of the 7th Int. Conference on Digita-
lAudio Effects. Naples, Italy.
P.X. Joris, P.H. Smith and T.C. Yin (1998) Coincidence
Detection in the Auditory Systems: 50 years after Jef-
fress In Neuron,Vol.21,December. Cell Press.
K. Nakadai, D. Matsuura H.G. Okuno and H. Kitano (2003)
Applying Scattering Theory to Robot Audition Sys-
tem: Robust Sound Source Localization and Extrac-
tion In In Proceedings of the 2003 IEEE Intl. Confer-
ence on Robots and Systems.
Berkout, de Vries and Boone (1980) A new method to ac-
quire impulse esponse in concert halls In J. Audio Eng.
Society 68(8).
A.Farina (2000) Simultaneous Measurement of Impulse
Response an Distorsion with a Swept-Sine Technique
In Proc. of the 108 AES Convention, 2000.
V.R. Algazi, R.O. Duda, D.M. Thompson and C. Avendano
(2001) The CIPIC HRTF Database In Proceedings of
IEEE Workshops on Application of Signal Processing
to Audio and Acoustics New York USA, 2001.
K. Nakadai, H.G. Okuno and H.Kitano (2001) Epipo-
lar Geometry Based Sound Localization and Ex-
traction for Humanoid Audition In Proceedings of
IEEE/RSJ Conference on Intelligent Robots and Sys-
tems. Maui,Hawaii,USA,2001.
J. Blauert (1997) In Spatial Hearing. MIT Press,USA.
C.H. Knapp and G.Clifford Carter (1976) The General-
ized Correlation Method for Time Delay Estimation
In IEEE Trans. Acoustic Speech and Signal Process-
ing, pp 320-327, Vol. 24.
P.Santangelo (2006) Sound Localization In Robotic Envi-
ronment Universit
`
a degli Studi di Napoli Federico II.
Thesis available by the author.
Irie, R. (1995) Robust sound localization: An application of
an auditory perception system for a humanoid robot”,
Master’s thesis, MIT Department of Electrical Engi-
neering and Computer Science
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
174
