
A ROBUST NON-LINEAR FACE DETECTOR
Antonio Rama, Francesc Tarrés
Dept. Teoria del Senyal i Comunicacions, Universitat Politècnica de Catalunya (UPC), Barcelona, Spain
Jacek Naruniec
Faculty of Electronics and Information Technology, Warsaw University of Technology (IPW), Warsaw, Poland
Keywords: Face detection, fuzzy integral, adaboost.
Abstract: A novel face detector using the non-linear Fuzzy
Integral operator is presented in this paper. The main
advantage of this method is that it has a much lower false detection rate with the same optimal set of
features as the state-of-the art Adaboost face detector. Furthermore, this novel face detector seems to have a
better generalization capability than the Adaboost method. Preliminary results show a positive face
detection rate higher than the 92% having a false detection rate lower than the 2% when using a four stage
cascade scheme.
1 INTRODUCTION
Face detection is a fundamental first-step in many
applications based on face processing, such as face
recognition, video coding, and intelligent human-
computer interfaces. The goal of this step consists in
detecting and localizing an unknown number of
faces in an image. Since human faces are rigid and
have high variability in size, shape, color, and
texture, face detection is still a difficult problem.
The proposed techniques can be broadly classified
into two main categories:
Kno
wledge-based methods. These algorithms
express the a priori information of the face in
terms of rules. Typically, these rules are based
on the relationships between the facial features
(Yang, 1994) (Yang, 2002).
A
ppearance-based methods. On the other hand,
this second group tries not to assume any prior
knowledge about the appearance of the face but
rather to extract some important features
directly from a representative training set of
faces. In other words, appearance-based
techniques incorporate the a priori information
of the face implicitly into the system through
training schemes (
Rowley, 1998), (Turk, 1991).
This category includes the state-of-the-art
AdaBoost face detector (Viola, 2001).
For a comprehensive review of face detection
m
ethods, the reader is referred to (Yang, 2002),
(Hjelmas 2001).
Face detection approaches should have two
im
portant properties: high performance and low
computational cost in the recognition stage. Usually,
face detection is the previous stage in a complete
face recognition system. Thus, the face should be
well localized, for a latter normalization step, and it
should also require a low percentage of the
processing time of the system since the recognition
stage demands usually a higher computational
burden, especially for huge databases. Adaboost face
detector fulfills the previous two requirements (fast
and robust); therefore it has been quite accepted for
real-time applications, like a control access point or
an intelligent cash machine.
In this paper we present a novel face detector
base
d on the non-linear Fuzzy Integral operator.
This technique, as preliminary results stated, could
be a good alternative to the Adaboost method.
The rest of the paper is organized as follows. In
sect
ion 2 and 3, the fundamentals of the Adaboost
method and the Fuzzy Integral operator are
reviewed. Section 4 describes the proposed Fuzzy
Integral face detector, whereas section 5 describes
the experiments performed so far and some
preliminary results. Finally, section 6 contains the
conclusions together with the future research.
421
Rama A., Tarrés F. and Naruniec J. (2007).
A ROBUST NON-LINEAR FACE DETECTOR.
In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 411-416
DOI: 10.5220/0002137704110416
Copyright
c
SciTePress
No
Face
Face
feature
θ
Decision
δ(O)
Sub-window
of the image
(24x24)
Compute
Feature
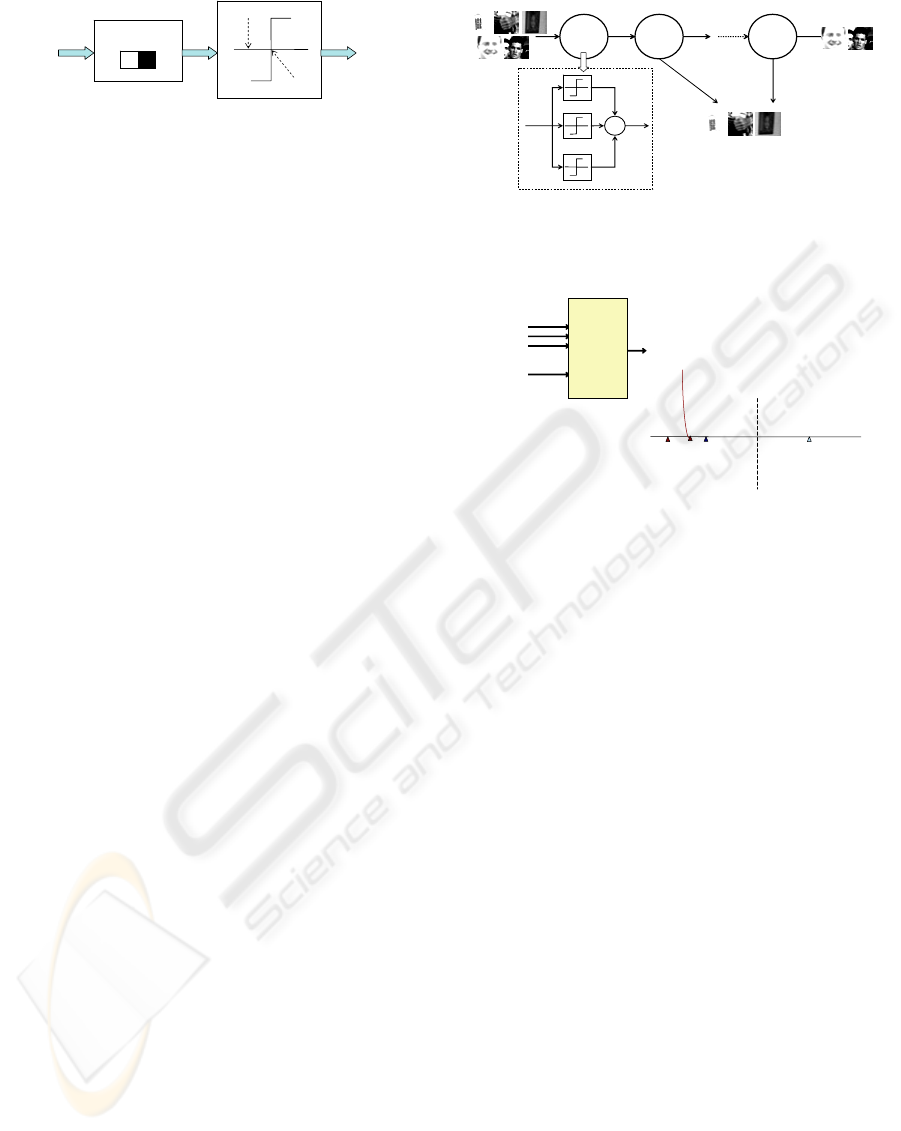
Figure 2: Adaboost cascade scheme.
Stage 1 Stage 2 Stage N
Face
.
.
+
STRONG
CLASSIFIER
Objects Rejected
(No face)
Figure 1: Adaboost weak classifier.
2 ADABOOST: A QUICK REVIEW
Object detection using AdaBoost classifier was
introduced by Viola and Jones (Viola, 2001). Their
face detection approach has shown how local
contrast features found in specific positions of the
object can be combined to create a strong face
detector. The main idea is that each feature (different
Haar filters at different positions of an image sub-
window) will be evaluated by a weak classifier in
order to decide if the sub-window corresponds to a
face (accept) or not (reject) as shown in Figure 1.
If the feature is above a certain threshold θ then the
sub-window will be classified as a face. Separately,
each weak classifier achieves a low performance but
when combining some of them into a strong
classifier the detection rate grows exponentially as
depicted in the dashed rectangle of Figure .
Non-Linear
Fuzzy
Integral
Face
Detector
Data Set
n features
(Haar Filters)
∫
⋅=
μ
dfY
ˆ
Nevertheless, although the detection rates of
a strong classifier can reach more than the 99%,
achieving very low false detection rate, computation
time of a very large set of features is very long. For
this reason, Viola and Jones proposed a cascade
scheme of strong classifiers like the one presented in
Figure . Each stage corresponds to a strong classifier
and is trained with all the examples that the previous
stage has misclassified plus some new ones. This
leads to an optimal selection of features in each
cascade which are able to detect always harder
examples. In other words, the first stages can discard
sub-windows which are very different from faces,
whereas the latter stages could reject more difficult
examples like balloons, soccer balls, etc… For more
details about the Adaboost face detection approach,
the reader is addressed to the original paper (Viola,
2001).
3 FUZZY INTEGRAL BASICS
The theory of Fuzzy Measures is based on the work
of Sugeno (Sugeno, 1974). The introduction of fuzzy
sets (Zadeh, 1965) encouraged the redefinition of set
measures. Sugeno achieved this
definition by introducing so-called fuzzy measures,
with respect to which fuzzy Integral can be defined.
Thus, fuzzy measures generalize classical measures,
i.e. probability measures. Here only a brief overview
of how fuzzy integral can be used for classification
problems is presented and the reader is addressed to
(Aureli, 2004) for more precise details. The main
idea is to use a fuzzy integral classifier with an
extended set of Haar features for face detection. The
fuzzy integral (Aureli, 2004) is a non-linear operator
that can be used as a classifier. Fuzzy Integrals are
generalizations of integral operators that include
non-linear operations on the data set. In the context
of classification, the most frequently used fuzzy
integrals are the Choquet integral and the Sugeno
integral. We propose to use a Choquet integral for
the data fusion process. The main ideas and the
process of computing the Choquet integral are given
hereafter:
Consider we have a vector of feature attributes
{
}
n
xxxX ,...,,
21
=
where x
i
may represent a pixel,
an audio sample or (as in our case) a haar feature at
a given position of the sub-window. Given this set of
features we collect a number of M samples for the
training stage. The attributes of the features at each
sample are represented by a vector:
(1)
Mapping from n features to real axis
threshold
NO FACE FACE
Figure 3: Fuzzy Integral face detector.
{
}
),...,,(),...,,(),...,(),(),(
32131321
xxxxxxxx
μ
μ
μ
μ
μ
μ
=
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
422
The Choquet integral consist in a two stage process:
Rearrangement of the feature values vector in
non decreasing order, such that
(2)
where is a certain permutation of
. And f(x
)',...,','(
21 n
xxx
),...,,(
21 n
xxx
i
’) can be any nonnegative
function on X.
The Choquet integral is then obtained by
computing:
(3)
The training of the classifier consists in selecting
the optimal fuzzy measures on the objective of
minimizing the misclassification rate. There are a
number of alternatives for estimating the fuzzy
measures but most of them are based on soft-
computing strategies. In this work, we are following
an approach based on neural networks for estimating
the set of fuzzy measures.
One of the interesting peculiarities of the Fuzzy
Integral as a classifier is that once the fuzzy
measures have been determined, the classification is
computationally very efficient. As depicted in
Figure the fuzzy integral maps the input set of
features to a unique scalar (real axis). Then
depending on a threshold, this mapped value is
classified as face (Class i) or no face (Class j).
Good performance of this method comes from
the use of the fuzzy measure and the relevant
nonlinear integral, since the nonadditivity of the
fuzzy measure reflects the importance of the feature
attributes, as well as their inherent interaction,
toward the discrimination of the points. In fact, each
feature attribute has a respective important index
reflecting its amount of contribution in the final
decision. Furthermore, the global contribution of
several feature attributes to the final classification is
not just the simple sum of the contribution of each
feature, but may vary nonlinearly. A combination of
the feature attributes may have a mutually
restraining or a complementary synergy effect on
their contributions toward the final decision. In fact,
this aspect of features being mutually restraining is
the explanation of why the fuzzy integral face
detector could reject the negative examples faster
than the state-of-the art Adaboost approach.
In the next section the proposed face detector
based on the Fuzzy Integral will be explained.
4 FACE DETECTOR BASED ON
THE FUZZY INTEGRAL
4.1 Feature Selection
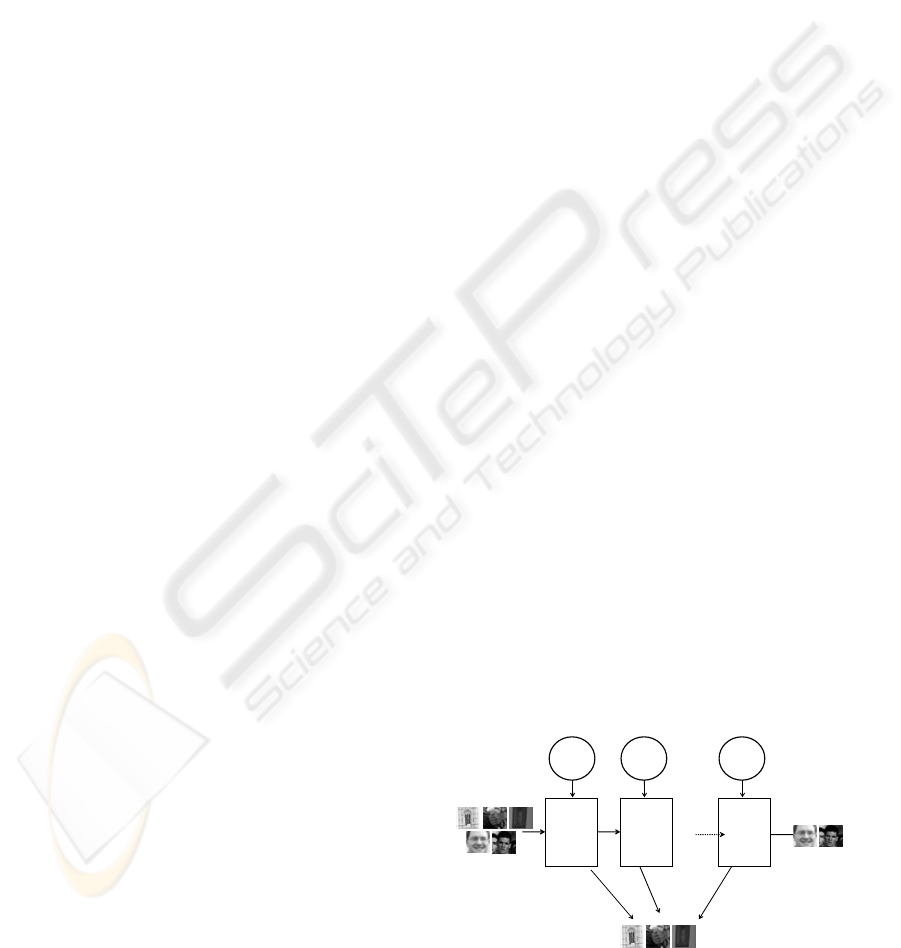
In this paper we propose a novel face detector based
on a cascade of Fuzzy Integral classifiers as depicted
in
Figure . One of the main drawbacks when using
the fuzzy integral is that the number of
computational operations grows exponentially with
the number of features used to train the system.
Thus, it will be impractical to train the system like in
(Viola, 2001) (Lienhart, 2002) considering all
possible positions of each Haar feature in each
image sub-window, i.e. 117,941 features for a 24x24
sub-window if we use the feature set depicted in
Figure (Lienhart, 2002). Thus, a Fuzzy Integral face
detector is proposed which uses the optimal subset
of features computed by the Adaboost approach. For
that, we have selected the following configuration of
the Adaboost approach after some exhaustive probes
(Braup, 2006):
11 stages of strong classifiers.
3325 face positive examples (the same set for
all stages) + 4500 negative examples in each
stage.
All set of features presented in
Figure .
Minimum face detection rate at each stage of
99.5%.
Maximum false detection rate at each stage of
30%.
Using this optimal configuration we train the system
and get the optimal subset of features for each stage.
For example, the first strong classifier (first stage) of
the Adaboost detector includes only 6 features:
Haar-Y2 at 3 different positions, Haar-X4 at 2
positions, and Haar-Y4 at one position. The same 6
features will be used to train the first stage fuzzy
integral classifier of the cascade scheme presented in
Figure .
Stage 1
Feature
Set 1
Face
Objects Rejected
(No face)
Fuzzy
Integral
FD
Stage 2
Fuzzy
Integral
FD
Feature
Set 2
Stage N
Fuzzy
Integral
FD
Feature
Set N
Figure 4: Fuzzy Integral Cascade Face detector.
'(f)'()'(
21 n
xxfxf
≤
⋅⋅≤≤
⋅
)
[]
{}()
∫
∑
=
+−
⋅−=⋅
n
i
niiii
xxxxfxfdf
1
11
',...,',')'()'(
μμ
A ROBUST NON-LINEAR FACE DETECTOR
423

Edge Features
Line
Features
Center Surround
Features
HaarX2
HaarX3
HaarX4
Tilted HaarX2
HaarY2
Tilted HaarY2
Tilted Point
Tilted
HaarX3
Tilted
HaarX4
Tilted
HaarY3
Tilted
HaarY4
HaarY3
HaarY4
Point
Figure 5: Feature Set used for training Adaboost.
4.2 Training Stage of the Fuzzy
Integral Face Detector
In (Aureli, 2004) and (Sugeno, 1974) genetic
algorithms have been proposed to train the system.
In our case, we use a learning algorithm based on the
following control equation:
(5)
where
)'(xf
are the feature values normalized by the
power of the features. This normalization function is
necessary to scale and balance the magnitudes of
diverse feature attributes such that an optimal match
of the feature attributes in the Choquet Integral
toward the classification can be found. These feature
values are then rearranged in non-decreasing order
as mentioned in Eq. 3, σ is the adaptive step size and
error is a parameter that can take the values -1, 0 or
1 depending on the decision of the classifier (0
means that the sample has been correctly classified).
And finally
)'(xfΔ
is the difference between all the
attributes involved in the fuzzy measure we are
updating.
5 EXPERIMENTS AND RESULTS
5.1 Face Database
All experiments have been carried out on a database
which is composed of 4000 face images which has
been previously normalized to a 24x24 pixel
resolution (see
Figure ). For the negative examples
more than 2000 images of different resolutions that
don’t contain any face have been downloaded from
the World Wide Web. Dividing these 2000 images
in 24x24 sub-windows leads to a total of more than
Figure 6: Positive examples of faces.
. The half of the positive examples and only 50000
of the 2M negative examples have been used to train
a 4-stage Fuzzy Integral Face Detector. The rest of
samples have been used as test samples.
5.2 Face Detection Results: 4-Stage
Classifier
A 4-stage fuzzy integral face detector has been
implemented. The 4 stages will use 6, 9, 11 and 21
different Haar features respectively. The positive
face detection rate is above the 92% but the most
impressive thing is that more than 99 % of the non-
faces have also been correctly discarded. The first
stage of the fuzzy integral cascade face detector
alone rejects more than the 95% of non-faces sub-
windows. Figure 8 and Figure 7 represents an
extreme example of this concept.
)'
Figure 8 represents the outputs of a one-, two-,
three-, and four-stages Adaboost cascade scheme,
whereas Figure represents a one-, two-, three-, and
four-stages Fuzzy Integral cascade scheme. For a
more fair comparison between both techniques, no
post-processing step for eliminating overlapped
windows has been used.
Results show that our method (Figure 7) detects
all faces and discard almost all negatives sub-
windows (only 7 positive negatives and 6
correspond to complete overlapped windows). On
the other hand, the Adaboost classifier detects also
all faces (one is not totally detected) but still more
than 25 non-faces are accepted (only half of them
are partially overlapped).
The fuzzy integral face detector shows a better
trade-off between detection rate and false detections.
This is especially remarkable in the first stages (top
pictures of Figures 7 and 8), where the Fuzzy
Integral face detector rejects more than the half of
false detections of the Adaboost approach.
Furthermore, continuing with this example, if more
stages are performed in the Adaboost classifier, the
(error ⋅⋅+
σ
))'(())'((
1
xfxfxf
ii
Δ=
+
μμ
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
424

Figure 7: Fuzzy Integral Results. (From Top to Bottom are
the outputs of the 1
st
, 2
nd
, 3
rd
and 4
th
stage Fuzzy Integral
face detector cascade scheme.).
best results are obtained for a 7-stages face detector
which rejects all non-faces but only detects 8 of the
10 faces of the image as illustrated in Figure . These
results are worse than the ones obtained for our 4-
stages Fuzzy Integral Face Detector. Nevertheless, it
should also be commented that if more stages of the
Fuzzy Integral Face Detector are implemented, the
two non-detected faces of Figure will be also
misclassified.
Figure 8: Adaboost Results. (From Top to Bottom are the
outputs of the 1
st
, 2
nd
, 3
rd
and 4
th
stage Adaboost cascade
scheme).
6 CONCLUSIONS AND FUTURE
WORK
In this paper a novel face detector approach based on
the non-linear Fuzzy Integral operator has been
presented. Preliminary results show a better trade-off
between positive detection and negatives detection
than state-of-the art Adaboost technique.
Nevertheless, the face detection rate is similar on
A ROBUST NON-LINEAR FACE DETECTOR
425

Figure 9: Best Results for Adaboost Face Detector (7
stages)
both approaches, so a more extended analysis of the
results should be done in order to determine under
which conditions or constraints one approach is
better than the other. This could lead to some hybrid
approach where both classifiers could be fused at
different levels (first stages using Fuzzy Integral,
and the latter ones Adaboost, or combining the
opinions of both classifiers).
Special attention should also be focused to the
training stage. One main drawback of the Fuzzy
Integral is that its computational cost during the
training stage grows up exponentially with the
number of features. Hence, it would not be possible
to train the system for all Haar-features in all
positions of the sub-window like explained in
Section 4.1. On the other hand, once the features
have been selected, the Fuzzy Integral face detector
needs fewer positive and negative samples than the
Adaboost approach. This could be foreseen as a
better generalization capability of the Fuzzy Integral
face detector.
Another important topic that should be also
analyzed is the values of the fuzzy measures. These
measures aim to evaluate the relative importance of
each feature in the final classification. So it would
be possible to reduce the set of features to an
optimal smaller subset by analyzing the fuzzy
measures. This would lead to a substantially
improvement of the computational cost required in
the detection stage since only the important ones
will be considered.
Finally, a complete study, of the computational
cost of each approach should be reported. In this
paper, no results of this aspect have been presented
since both techniques have been implemented under
different frameworks with different programming
languages.
Summarizing, the proposed novel technique not
only shows very promising results but also opens
some new issues that could be exploded in order to
get even better results.
ACKNOWLEDGEMENTS
The work presented was developed within VISNET
II, a European Network of Excellence funded under
the European Commission IST FP6 programme.
REFERENCES
Yang, G., and Huang, T. S., 1994. “Human Face
Detection in Complex Background” in Pattern
Recognition, vol. 27, no. 1, pp. 53-63.
Yang, M.-H., Kriegman, D. and Ahuja, N., 2002.
“Detecting Faces in images: a Survey”, in IEEE
Transactions on Pattern Analysis and Machine
Intelligence 24, nº1, pp.34-58.
Rowley, H. A., Baluja, H. A., and Kanade, T., 1998.
“Neural network-based face detection”, in IEEE
Transactions Pattern Analysis and Machine
Intelligence 20, 23–38.
Turk, M. A., Pentland, A. P., 1991. “Face recognition
using eigenfaces”, in Proceedings of the IEEE
Computer Society Conf. on Computer Vision and
Pattern Recognition, pp. 586-591, Maui, Hawaii.
Viola P., Jones M., 2001. “Rapid Object Detection using a
Boosted Cascade of Simple Features, in Computer
Vision and Pattern Recognition.
Hjelmas, E., and Low, B. K., 2001. “Face Detection: A
Survey”, in Computer Vision and Image
Understanding, vol. 83, no. 3, pp. 236-274.
Sugeno, M., 1974. “The Theory of Fuzzy Integrals and Its
Applications”, PhD thesis, Tokyo Institute of
Technology, Japan.
Zadeh, L. A., 1965. „ Fuzzy sets“, Information Control,
pp. 338–353.
Aureli Soria-Frisch, 2004. “Soft Data Fusion in Computer
Vision”, PdD thesis, Fraunhofer Institut fuer
Produktionsanlagen und Konstruktionstechnik, Berlin,
Germany.
Lienhart, R., and Maydt, J., 2002. “An Extended Set of
Haar-like Features for Rapid Object Detection”. in
IEEE International Conference on Image Processing
2002, Vol. 1, pp. 900-903, Sep. 2002.
Braup, J. M., Tarres, F., 2006. “Anàlisi de vídeo per la
detecció automàtica de cares”. Master Thesis in
Catalan at the Technical University of Catalonia –
Escola Politècnica Superior de Castelldefels.
SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications
426
