A NEW ADAPTIVE CLASSIFICATION SCHEME BASED ON

SKELETON INFORMATION

Catalina Cocianu

Dept. of Computer Science, Academy of Economic Studies, Bucharest, Romania

Calea Dorobantilor #15-17, Bucuresti –1, Romania

Luminita State

Dept. of Computer Science, University of Pitesti,Pitesti, Romania

Caderea Bastliei #45, Bucuresti – 1, Romania

Ion Roşca

Dept. of Computer Science, Academy of Economic Studies, Bucharest, Romania

Calea Dorobantilor #15-17, Bucuresti –1, Romania

Panayiotis Vlamos

Ionian University, Corfu, Greece

Keywords: Principal axes, supervised learning, pattern recognition, data mining, classification, skeleton.

Abstract: Large multivariate data sets can prove difficult to comprehend, and hardly allow the observer to figure out

the pattern structures, relationships and trends existing in samples and justifies the efforts of finding suitable

methods from extracting relevant information from data. In our approach, we consider a probabilistic class

model where each class

Hh ∈ is represented by a probability density function defined on

; where n is

the dimension of input data and H stands for a given finite set of classes. The classes are learned by the

algorithm using the information contained by samples randomly generated from them. The learning process

is based on the set of class skeletons, where the class skeleton is represented by the principal axes estimated

from data. Basically, for each new sample, the recognition algorithm classifies it in the class whose skeleton

is the “nearest” to this example. For each new sample allotted to a class, the class characteristics are re-

computed using a first order approximation technique. Experimentally derived conclusions concerning the

performance of the new proposed method are reported in the final section of the paper.

1 INTRODUCTION

Large multivariate data sets can prove difficult to

comprehend, and hardly allow the observer to figure

out the pattern structures, relationships and trends

existing in samples. Consequently, it is useful to find

out appropriate methods to summarize and extract

relevant information from data. This is becoming

increasingly important due to the size possibly

excessive large of high dimensional data.

Several authors refer to unsupervised

classification or data clustering as being the process

of investigating the relationships within data in order

to establish whether or not it is possible to compress

the information that is to validly summarize it in

terms of a relatively small number of classes

comprising similar objects in some sense (Gordon,

1999). In such a case, the whole collection given by

such a cluster can be represented by a small number

of class prototypes.

The word ‘classification’ is also used to define

the assignment process of objects to one of a set of

given classes. Thus, in pattern recognition or

discriminant analysis (Ripley, 1996; Hastie,

Cocianu C., State L., Ro ¸sca I. and Vlamos P. (2007).

A NEW ADAPTIVE CLASSIFICATION SCHEME BASED ON SKELETON INFORMATION.

In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 85-92

DOI: 10.5220/0002137900850092

 SciTePress

Tibshirani &al, 2001) each object is assumed to

come from one of a known set of classes, the

problem being to infer the true class for each data.

The test performed on data are based on a finite

feature set determined either by mathematical

techniques or empirically using a training set

containing data whose true classifications are

known.

During the past decade the classification and

assignment procedures have both found a large

series of applications related to information

extraction from large size data sets, this field being

referred as data mining and knowledge discovery in

databases. (Fayyad&al, 1996; Hastie, Tibshirani

&al, 2001)

Since similarity plays a key role for both

clustering and classification purposes, the problem

of finding a relevant indicators to measure the

similarity between two patterns drawn from the

same feature space became of major importance.

The most popular ways to express the

similarity/dissimilarity between two objects involve

distance measures on the feature space. (Jain, Murty,

Flynn, 1999). In case of high dimensional data, the

computation complexity could become prohibitive,

consequently the use of simplified schemes based on

principal components, respectively principal

coordinates, provides good approximations. (Chae,

Warde, 2006) Recently, alternative methods as

discriminant common vectors, neighborhood

components analysis and Laplacianfaces have been

proposed allowing the learning of linear projection

matrices for dimensionality reduction. (Liu, Chen,

2006; Goldberger, Roweis, Hinton, Salakhutdinov,

2004)

2 DISCRIMINANT ANALYSIS

There are several different ways in which linear

decision boundaries among classes can be stated. A

direct approach is to explicitly model the boundaries

between the classes as linear. For a two-class

problem in a n-dimensional input space, this

amounts to modeling the decision boundary as a

hyperplane that is a normal vector an a cut point.

One of the methods that explicitly looks for

separating hyperplanes is the well known perceptron

model of Rosenblatt (1958), that yielded to an

algorithm that finds a separating hyperplane in the

training data if one exists.

Another method, due to Vapnik (1996) finds an

optimally separating hyperplane if one exists, else

finds a hyperplane that minimizes some measures of

overlap in the training data.

In the particular case of linearly separable

classes, in discriminating between two classes, the

optimal separating hyperplane separates and

maximizes a distance to the closest point from either

class. Not only does this provide an unique solution

to the separating hyperplane problem, but by

maximizing the margin between the two classes on

the training data this leads to better classification

performance on test data and generalization

capacities.

When the data are not separable, there will be

now feasible solutions to this problem, and

alternative formulation is needed. The disadvantage

of enlarging the space using basis transformations is

that an artificial separation through over-fitting

usually results. A more attractive alternative seems

to be the support vector machine (SVM) approach,

which allows for overlap but minimizes a measures

of the extent of this overlap.

The basis expansion method represents the most

popular technique for moving beyond linearity. It is

based on the idea of augmenting/replacing the vector

of inputs with additional variables which are

transformations of it and the use of linear models in

the augmented new space of derived input features.

The use of the basis expansions allows the

achievement of more flexible representations of

data. Polynomials, also there are limited by their

global nature, piecewise-polynomials and splines

that allow for local polynomial representations,

wavelet basis, especially useful for modeling signals

and images are just few examples of sets of basis

functions. All of them produce a dictionary

consisting of typically a very large number of basis

functions, far more than one can afford to fit to data.

Along with the dictionary, a method is required for

controlling the complexity of the model using basis

functions from the dictionary. Some of the most

popular approaches are restriction methods, where

we decide before-hand to limit the class of functions,

selections methods, which adaptively scan the

dictionary and include only those basis functions

that contribute significantly to the fit of the model

and regularization methods (as, for instance, Ridge

regression), where the entire dictionary is used but

restrict the coefficients.

Support Vector Machines (SV) are an algorithm

introduced by Vapnik and coworkers theoretically

motivated by VC theory. (Cortes, Vapnik, 1995;

Friess, Cristianini & al., 1998) SVM algorithm

works by mapping training data for classification

tasks into a higher dimensional feature space. In this

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

new feature space the algorithm looks for a maximal

margin hyperplane which separates the data. This

hyperplane is usually found using a quadratic

programming routine which is computationally

intensive, and it is non trivial to implement. SVM

have a proven impressive performance on a number

of real world problems such as optical character

recognition and face detection. However, their

uptake has been limited in practice because of the

mentioned problems with the current training

algorithms. (Cortes, Vapnik, 1995; Friess,

Cristianini & al., 1998)

The support vector machine classifier is an

extension of this idea, where the dimension of the

enlarged space is allowed to get very large, infinite

in some cases. (Hastie, Tibshirani &al, 2001)

3 PRINCIPAL DIRECTIONS -

BASED ALGORITHM FOR

CLASSIFICATION PURPOSES

The developments are performed in the framework

of a probabilistic class model where each class

Hh ∈ is represented by a probability density

function defined on

; where n is the dimension

of input data and H stands for a given finite set of

classes. The classes are learned by the algorithm

using the information contained by samples

randomly generated from them. The learning process

is based on the set of class skeletons, where the class

skeleton is represented by the principal axes

estimated from data. Basically, for each new sample,

the recognition algorithm classifies it in the class

whose skeleton is the “nearest” to this example.

(State, Cocianu 2006).

Let X be a n-dimensional random vector and let

X(1), X(2),… ,X(N), be a Bernoullian sample on X .

We assume that the distribution of X is unknown,

except the first and second order statistics. More

generally, when this information is missing, the first

and second order statistics are estimated from the

samples.

Let Z be the centered version of X, Z = X -

E(X). Let

WWW ,...,,

be a set of linear

independent vectors and

()

WWWW ,...,,

= . We

denote by

y =

, nm ≤≤1 . The principal

axes of the distribution of X are

ψψψ ,...,,

such

that

()

y SWW

sup

∈

(1)

where S is the covariance matrix of Z.

According to the celebrated Karhunen-Loeve

theorem, the solution of (1) are unitary eigen vectors

of S,

ψψψ ,...,,

, corresponding to the eigen

values

≥≥≥ ...

Once a new sample is allotted to a class, the class

characteristics (the covariance matrix and the

principal axes) are modified accordingly using first

order approximations of the new set of principal

axes. In order to compensate the effect of the

cumulative errors coming from the first order

approximations, following to the classification of

each block of

PN samples, the class skeletons are re-

computed using an exact method.

Let

XXX ,...,,

be a sample from a certain

class

C. The sample covariance matrix is

()()

∑

−−

−

=Σ

NiNiN

ˆˆ

μμ

, (2)

where

∑

We denote by

λλλ

≥≥≥ ...

the eigen

values and by

ψψ

,...,

a set of orthonormal eigen

vectors of

N+1

is a new sample, then, for the series

121

,,...,,

+NN

XXXX , we get

()()

−−−

+Σ=Σ

+++

NNNNNN

μμ

ˆˆ

111

Σ−

(3)

Lemma

. In case the eigen values of

are

pairwise distinct, the following first order

approximations hold,

(

)()

ψΣψψΣψ

ˆˆ

=Δ+=

λλ

(4)

(

)

∑

≠

−

ψΣψ

ψψ

λλ

(5)

Proof

See (State, Cocianu , 2006 ).

The basis of the learning scheme can be described as

follows (State, Cocianu , 2006). The skeleton of C is

represented by the set of estimated principal axes

ψψ

,...,

When the example X

N+1

is included in C, then the

new skeleton is

,...,

++ N

ψψ

The skeleton disturbance induced by the decision

that X

N+1

has to be alloted to C is measured by

(

)

∑

ψψ

(6)

A NEW ADAPTIVE CLASSIFICATION SCHEME BASED ON SKELETON INFORMATION

The classification procedure identifies for each

example the nearest cluster in terms of the measure

(6). Let

{}

CCCH ,...,,

= . In order to protect

against misclassifications due to insufficient

“closeness” to any cluster, a threshold T>0 is

imposed, that is the example X

N+1

is alloted to one of

for which

()

∑

ψψ

()

∑

≤≤

min

ψψ

(7)

and D<T, where the skeleton of C

j ,,1

,...,

ψψ

The classification of samples for which the

resulted value of D is larger than T is postponed and

the samples are kept in a new possible class CR. The

reclassification of elements of CR is then performed

followed by the decision concerning to either

reconfigure the class system or to add CR as a new

class in H.

For each new sample allotted to a class, the class

characteristics (the covariance matrix and the

principal axes) are re-computed using (5) and (6).

The skeleton of each class is computed using an

exact method,

M, in case PN samples have been

already classified in

{}

CCCH ,...,,

= . The

adaptive classification scheme summarized as

follows.

Let

C , be the set of samples coming from the

i class, Mi ≤≤1 ;

{

}

CCCH ,...,,

is the set

of pre-specified classes.

Input:

{}

CCCH ,...,,

REPEAT

i←1

Step 1: Let X be a new sample. Classify X according

to (7)

Step 2: If

Mi ≤≤∃1 such that X is allotted to

C ,

then

2.1.re-compute the characteristics of

C using (3), (4)

and (5)

2.2. i++

Step 3: If i<PN goto Step 1

Else

3.1. For i=

M,1 , compute the characteristics of

class

C using M. 3.2. goto Step 1.

UNTIL THE LAST NEW SAMPLE HAS BEEN

CLASSIFIED

Output: The new set

{}

CRCCC

∪,...,,

4 EXPERIMENTAL ANALYSIS

A series of tests were performed on bidimensional

simulated data coming from 4 clases. We use a

probabilistic model, each class being represented by

a normal density function. The closeness between

each pair of classes is measured by the Mahalanobis

distance. The estimation of the principal directions is

based exclusively on data.

The classification criterion is: allote X

N+1

C if

()

∑

ψψ

()

∑

≤≤

min

ψψ

(8)

Because the size of the initial sample is relatively

small, we used small values of PN to compensate the

effect of the cumulative errors coming from the first

order approximations. Once a sufficient number of

new simulated examples correctly classified,

increasing values of PN are considered next.

The aims in performed tests were twofold. On

one hand it was aimed to point out the effects on the

performance of global/local closeness of the system

of classes and, on the other hand, the effects of the

geometric configurations of the principal directions

corresponding to the given classes. Some of the

results are presented in the following.

Test 1. In case the system of classes consists in four

classes, for each

≤

i , the class

C ~

()

N Σμ , ,

≤

i , where

μ = [10 -12],

⎥

⎦

⎤

⎢

⎣

⎡

2.50 1.65

1.65 3.49

μ = [1 1],

⎥

⎦

⎤

⎢

⎣

⎡

6.8066 5.6105

5.6105 6.6841

μ = [-10 0],

⎥

⎦

⎤

⎢

⎣

⎡

2.50 1.35

1.35 1.69

μ = [-8 24],

⎥

⎦

⎤

⎢

⎣

⎡

12.2789 1.02

1.02 6.2789

We assume that the initial sample contains 200

examples coming from each class.

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

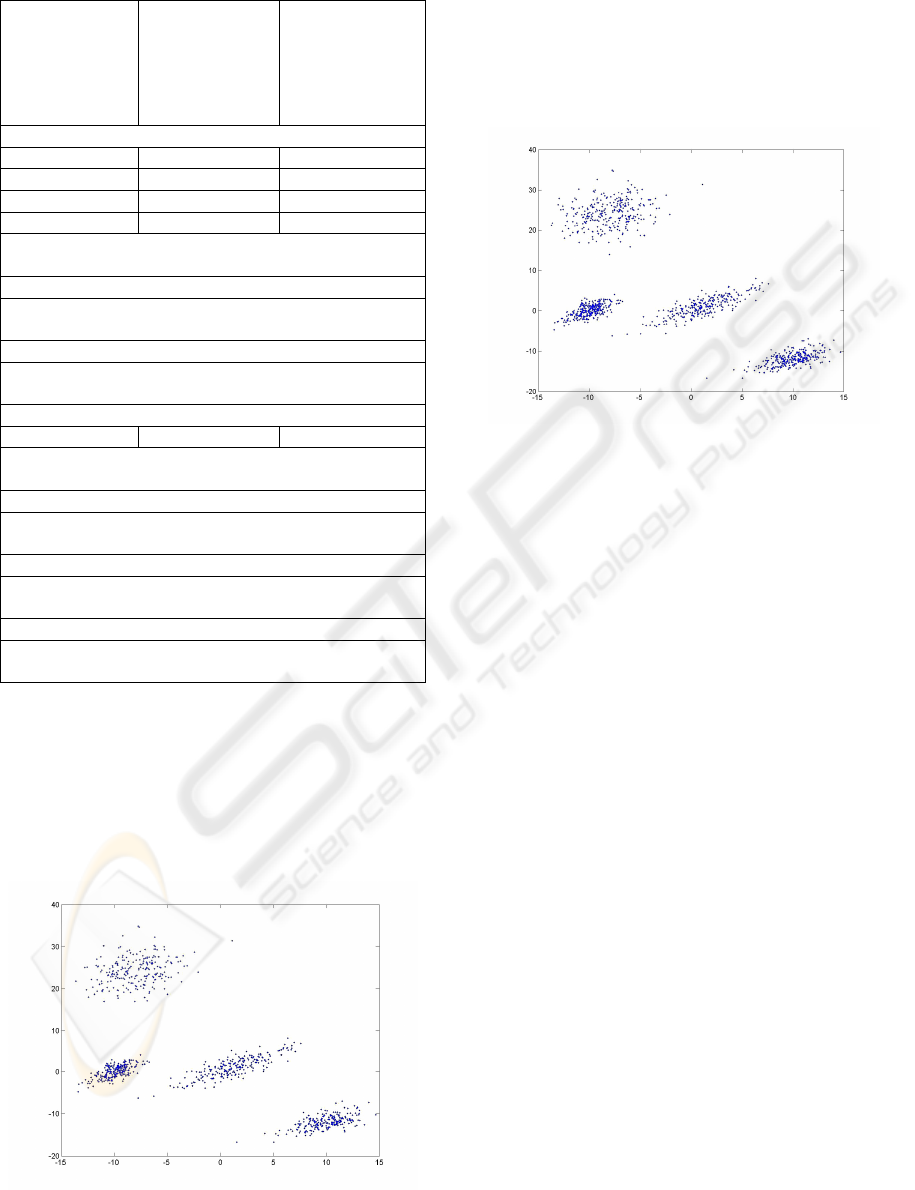
Table 1: Results on new simulated samples.

The index of

the sample in

the test set

The

misclassificatio

(the correct

class → the

alloted class)

Misclassified

examples

The first test set containing 20 new examples (PN=20)

2 3→2 (-7.02, 1.9)

5 4→2 (-10.06, 16.90)

14 3→2 (-7.11, 2.61)

20 4→2 (-6.38, 20.76)

4 misclassifications. For each class, compute the exact

values of its characteristics

The second test set containing 20 new examples

No misclassification. For each class, compute the exact

values of its characteristics

The third test set containing 50 new examples (PN=50)

No misclassification. For each class, compute the exact

values of its characteristics

The fourth test set containing 50 new examples

23 4→2 (-5.99, 15.88)

1 misclassified example. For each class, compute the

exact values of its characteristics

The fifth test set containing 50 new examples

No misclassification. For each class, compute the exact

values of its characteristics

The sixth test set containing 50 new examples

No misclassification. For each class, compute the exact

values of its characteristics

The seventh test set containing 50 new examples

No misclassification. For each class, compute the exact

values of its characteristics

The Mahalanobis distances between classes are

given by the entries of the matrix

⎥

⎦

⎤

⎢

⎣

⎡

0 39.4249 54.7989 152.3496

39.4249 0 33.2818 247.6876

54.7989 33.2818 0 99.4061

152.3496 247.6876 99.4061 0

Figure 1: The initial sample.

Note that in this example the system of classes is

relatively well separated. The tests on the

generalization capacities yielded the results

presented in table 1.

The initial sample is depicted in Figure 1. The

clusters resulted at the end of the tests are depicted

in Figure 2.

Figure 2: The clusters resulted at the end of the tests.

Test 2. In case the system of classes consists in four

classes, for each

≤

i , the class

C ~

()

N Σμ , ,

≤

i , where

μ = [10 -12],

⎥

⎦

⎤

⎢

⎣

⎡

2.50 1.65

1.65 3.49

μ = [1 10],

⎥

⎦

⎤

⎢

⎣

⎡

6.8066 5.6105

5.6105 6.6841

μ = [-10 0],

⎥

⎦

⎤

⎢

⎣

⎡

2.50 1.35

1.35 1.69

μ = [-8 4],

⎥

⎦

⎤

⎢

⎣

⎡

12.2789 1.02

1.02 6.2789

We assume that the initial sample contains 200

examples coming from each class.

The Mahalanobis distances between classes are

given by the entries of the matrix

⎥

⎦

⎤

⎢

⎣

⎡

0 1.3258 6.3728 64.3167

1.3258 0 14.6578 247.6876

6.3728 14.6578 0 203.7877

64.3167 247.6876 203.7877 0

Note that the system of classes is such that C

, C

are pretty “close” and C

is well separated

from the others. As it is expected, the

misclassifications occur mainly for samples coming

from C

, C

A NEW ADAPTIVE CLASSIFICATION SCHEME BASED ON SKELETON INFORMATION

The initial sample is depicted in Figure 3 and the

clusters resulted at the end of the classification steps

are presented in Figure 4.

The closest classes in the sense of Mahalanobis

distance are C

and C

. Note that correlations of the

components are almost the same in C

and C

, but

the variability along each of the axes are

considerably larger in case of C

than C

In order to evaluate the capacities of our method

we tested its classification performance in

discriminating between C

and C

against the

classical discriminant algorithm. The Kolmogorov-

Smirnoff and MANOVA tests were applied to each

test set in order to derived statistical conclusions

about the closeness degree of the set of misclassified

sample and each of the classes C

, C

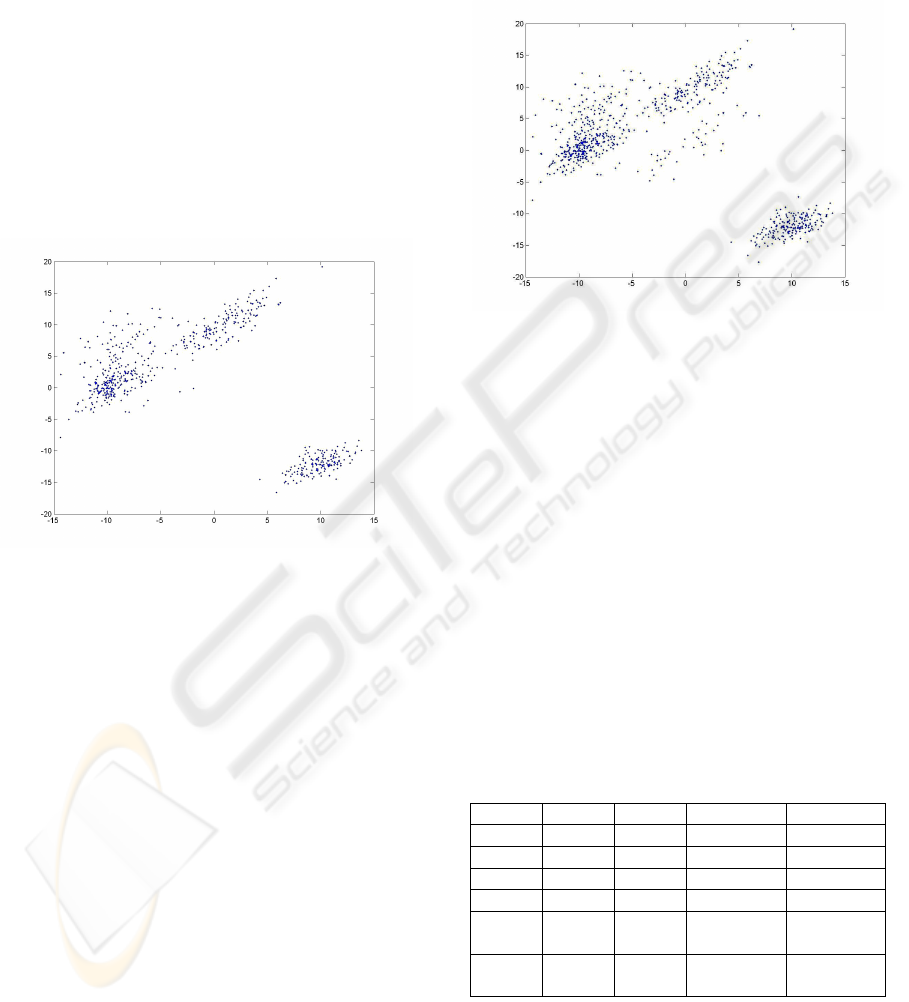
Figure 3: The initial sample.

The tests were performed on several randomly

generated samples of size 1000.

Some of the results obtained on samples coming

from C

and classified in C

are summarized in

Table 2. The entries of the table have the following

meaning. Each column corresponds to a test set. The

row entries are:

¾ the number of misclassified examples in case of

our method;

¾ the number of misclassified examples by

classical discriminant analysis method (CDA);

¾ the number of examples misclassified by our

method and misclassified by CDA;

¾ the results of Kolmogorov-Smirnoff test applied

for the group of misclassified examples against

the class identified by our classification

procedure.

¾ the results of Kolmogorov-Smirnoff test applied

for the group of misclassified examples against

the true class;

¾ the results of MANOVA applied for the group

of misclassified examples against the class

identified;

¾ the results of MANOVA applied for the group

of misclassified examples against the true class.

Figure 4: The clusters resulted at the end of the

classification steps

Each component of the results obtained by

Kolmogorov-Smirnoff test is either 0 or 1 indicating

for each coordinate the acceptance/rejection of the

null hypothesis using only this variable.

The test was applied on the transformed

examples such that the variables are decorrelated

using the features extracted from the misclassified

samples. The information computed by MANOVA

is summarized by retaining two indicators; the

former is either 0 or 1 and represents non-

rejection/rejection of the hypothesis that the means

are the same, but non rejection of the hypothesis

they lie on a line, the latter being the value of

Mahalanobis distance between the considered

groups.

Table 2: Some of the results obtained on samples coming

from C

and classified in C

Note that the performances proved by our

method are far better as compared to the classical

discriminant analysis in this case. Similar results

were obtained in a long series of tests performed in

76 67 65 76 78

132 116 122 135 132

76 67 65 76 78

1,1 1,1 1,1 1,1 1,1

0,1 0,1 0,1 0,1 1,1

0.095

0.101

0.125

0.105

0.095

4.50

4.199

3.898

4.408

4.790

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

discriminating between two classes almost

undistinguishable, where the variability in the

second class (in our case C

) is significant larger

than in the first class (in our case C

In Table 3 and Table 4 are summarized the

results obtained in applying the same method to the

samples coming from C

and misclassified in C

The entries of the Table 3 and Table 4 have the same

meaning as in Table 2.

In this case, our method and the classical

discriminant analysis method have close behaviors.

Table 3: Some of the results obtained on samples coming

from C

and misclassified in C

208 213 185 231 207

246 248 217 275 248

206 210 181 230 206

1,0 1,0 1,0 1,0 1,0

0,1 0,1 0,1 0,1 0,1

0.147

0.163

0.242

0.132

0.202

2.792

2.64

2.461

3.001

2.697

Table 4: Some of the results obtained on samples coming

from C

and misclassified in C

328 293 334 317 319

266 256 276 264 271

258 244 266 253 264

1,0 1,0 1,0 1,0 1,0

0,1 0,1 0,1 0,1 0,1

0.349

0.175

0.228

0.2932

0.232

2.616

2.555

2.624

2.435

2.577

Test 3

. The system of classes is well separated

and principal directions are pairwise orthogonal. For

each

41 ≤≤ i , the class

C ~

()

N Σμ , , 41

≤

i ,

where

μ = [1 19], =

⎥

⎦

⎤

⎢

⎣

⎡

2.5000 1.6500

1.6500 3.4900

μ = [4 8], =

⎥

⎦

⎤

⎢

⎣

⎡

−

0.5814 0.2749-

0.2749- 0.4165

μ = [-7 3], =

⎥

⎦

⎤

⎢

⎣

⎡

2.5000 1.3500

1.3500 1.6900

μ = [11 -12], =

⎥

⎦

⎤

⎢

⎣

⎡

−

0.7034 0.5619-

0.5619- 1.0406

We assume that the initial sample contains 200

examples coming from each class.

The Mahalanobis distances between classes are

given by the entries of the matrix

⎥

⎦

⎤

⎢

⎣

⎡

0 255.7000 112.8035 378.9131

255.7000 0 86.7399 45.2959

112.8035 86.7399 0 142.1112

378.9131 45.2959 142.1112 0

We used the values PN=50 for the first 2 steps

and PN=100 for the next steps. The performed tests

reported no misclassification.

The initial sample is depicted in Figure 5 and the

clusters resulted at the end of for classification steps

are presented in Figure 6.

Figure 5: The initial sample.

Figure 6: The clusters resulted at the end of the

classification procedure.

REFERENCES

Cortes, C., Vapnik, V., 1995. Support Vector networks. In

Machine Learning 20: 273-297

Diamantaras, K.I., Kung, S.Y., 1996. Principal

Component Neural Networks: theory and applications,

John Wiley &Sons

A NEW ADAPTIVE CLASSIFICATION SCHEME BASED ON SKELETON INFORMATION

Everitt, B. S., 1978. Graphical Techniques for

Multivariate Data, North Holland, NY

Fayyad, U.M., Piatetsky-Shapiro, G., Smyth, P., and

Uthurusamy, R., 1996. Advances in Knowledge

Discovery and Data Mining, AAAI Press/MIT Press,

Menlo Park, CA.

Frieß, T., Cristianini, N., and Campbell, C., 1998. The

kernel adatron algorithm: A fast and simple learning

procedure for support vector machines. In 15th Intl.

Conf. Machine Learning. Morgan Kaufmann

Publishers

Goldberger, J., Roweis, S., Hinton, G., Salakhutdinov, R.,

2004. Neighbourhood Component Analysis. In

Proceedings of the Conference on Advances in Neural

Information Processing Systems

Gordon, A.D. 1999. Classification, Chapman&Hall/CRC,

Edition

Hastie, T., Tibshirani, R., Friedman, J. 2001. The Elements

of Statistical Learning Data Mining, Inference, and

Prediction. Springer-Verlag

Hyvarinen, A., Karhunen, J., Oja, E., 2001. Independent

Component Analysis, John Wiley &Sons

Jain,A.K., Dubes,R., 1988. Algorithms for Clustering

Data, Prentice Hall,Englewood Cliffs, NJ.

Jain, A.K., Murty, M.N., Flynn, P.J. 1999. Data clustering:

a review. ACM Computing Surveys, Vol. 31, No. 3,

September 1999

Krishnapuram, R., Keller,J.M., 1993. A possibilistic

approach to clustering. IEEE Trans. Fuzzy Syst., 1(2)

Liu, J., and Chen, S. 2006. Discriminant common vectors

versus neighbourhood components analysis and

Laplacianfaces: A comparative study in small sample

size problem. Image and Vision Computing 24 (2006)

249-262

Panayirci,E., Dubes,R.C., 1983. A test for

multidimensional clustering tendency. Pattern

Recognition,16, 433-444

Smith,S.P., Jain,A.K., 1984. Testing for uniformity in

multidimensional data, In IEEE Trans.`Patt. Anal.`

and Machine Intell., 6(1),73-81

State, L., Cocianu, C., Vlamos, P, Stefanescu, V., 2006.

PCA-Based Data Mining Probabilistic and Fuzzy

Approaches with Applications in Pattern Recognition.

In Proceedings of ICSOFT 2006, Portugal, pp. 55-60.

Ripley, B.D. 1996. Pattern Recognition and Neural

Networks, Cambridge University Press, Cambridge

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications