LOCAL DISSONANCE MINIMIZATION IN REALTIME

Juli

an Villegas and Michael Cohen

University of Aizu - Spatial Media Group; Aizu-Wakamatsu, Fukushima-ken, 965-8580, Japan

Keywords:

Adaptive microtuning, local consonance, SPSA, Pd, tonotopic dissonance.

Abstract:

This article discusses the challenges of applying the tonotopic consonance theory to minimize the dissonance

of concurrent sounds in real-time. It reviews previous solutions, proposes an alternative model, and presents a

prototype programmed in Pd that aims to surmount the difﬁculties of prior solutions.

1 INTRODUCTION

Perfect consonance can be achieved naturally using

non-ﬁxed tuning instruments such as the trombone.

However, for ﬁxed tuning instruments such as key-

boards, there is no practical way to change tunings

during a performance. Therefore, when ﬁxed and

non-ﬁxed tuning instruments play together, the or-

chestral temperament is necessarily the one used for

ﬁxed-tuning instruments. This fact limits the ability

of the ensemble to achieve perfect consonance.

Minimizing dissonance has been a topic of inter-

est for about six centuries. Some early approaches

tried to adjust the number of steps in the musical scale

so that combinations of different steps produced more

consonant chords in a given context. Scales with

fewer notes – e.g., pentatonic scales – didn’t work

well with western preferences of harmony. Scales

with more than twelve steps, like 36-noted scales used

in the Renaissance, incurred unwanted performance

difﬁculty. Recent developments use DSP techniques

to adjust incoming sounds to the nearest tone in a

scale template. This adjustment is done in real-time

and is widely used in software and recording studios.

Contemporaneous with these approaches is adap-

tive tuning, or adjustment of local consonance, a tech-

nique in which each tuning of concurrent notes is ad-

justed to achieve minimum dissonance possible at a

given time. Advantages of adaptive tuning include

that a template is unnecessary, and that it can mini-

mize the dissonance of non-harmonic sounds.

Adoption of this technique is limited for a couple

of reasons. First, implementations that utilize MIDI

must work around its limitations as explained later in

this article. Second, most of these implementations

assume a spectrum independent of frequency. This is

not true for real instruments for which spectrum can

change depending on pitch, intensity, etc.

2 DISSONANCE

Dissonance is generally understood as the absence

of consonance. Huron deﬁnes consonance as “the

subjective experience of pleasantness, euphonious-

ness, smoothness, fusion, or relaxedness evoked by

sounds” (Huron, 2006). A single theory to explain the

perception of consonance remains elusive.

The tonotopic theory of dissonance was ﬁrst

proposed by Greenwood (Greenwood, 1961b) and

independently advanced by Plomp and Levelt

(Plomp and Levelt, 1965). It is related to the work of

Helmholtz (v. Helmholtz, 1954), who observed that

dissonance can be explained in terms of ‘roughness’

and ‘beats’ of partials of simultaneous sounds. For

Helmholtz, a difference of tonal frequencies that pro-

duces a maximum dissonance was constant along the

hearing spectrum (frequency-independent.)

Using data from experiments in which subjects

were asked to rate the consonance of a sinewave dyad,

Plomp and Levelt concluded that the transition range

Villegas J. and Cohen M. (2007).

LOCAL DISSONANCE MINIMIZATION IN REALTIME.

In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 93-100

DOI: 10.5220/0002138800930100

 SciTePress

between consonant and dissonant intervals is related

to the critical bandwidth. Speciﬁcally, they claimed

that the maximum unpleasantness arises between two

sinewaves separated by 25 percent of a critical band,

adopting the concept of critical band described in

(E. Zwicker et al., 1957). According to them, the dis-

sonance of the dyad grows quickly from zero at the

unison and disappears as the interval exceeds one crit-

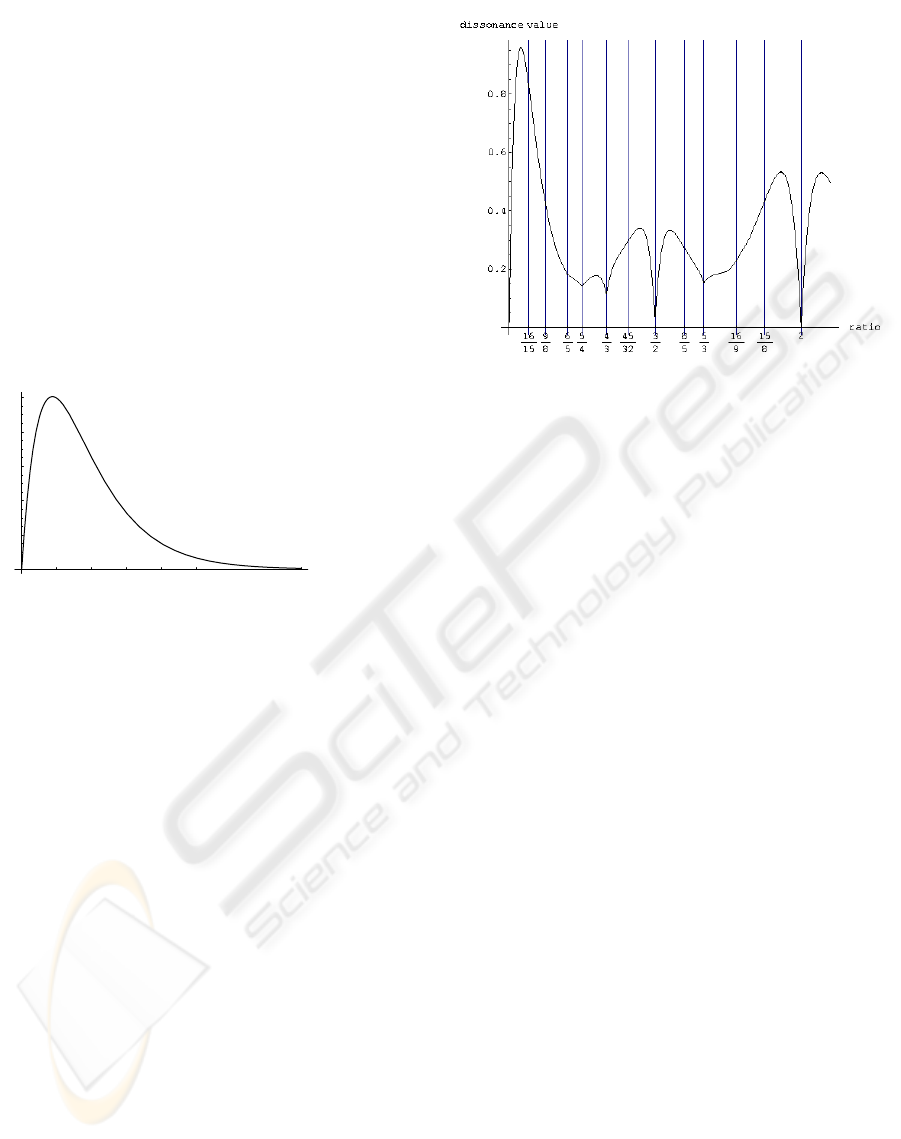
ical bandwidth, as shown in Figure 1. Furthermore,

Plomp and Levelt supposed that for complex timbres

the overall dissonance for a given interval was the ag-

gregate sum of the interactions between all of the con-

stituent partials. Figure2 shows the dissonance curve

of a complex tone according to their ﬁndings. The

0.25 0.5 0.75

1.25 2

critical bands

0.2

0.4

0.6

0.8

dissonance

Figure 1: Averaged dissonance curve of a dyad.

approach of Plomp and Levelt fails to explain why, in

the case of simple sine-waves, an interval sometimes

perceived as dissonant, like a M7 (major seventh), has

a smaller ‘dissonance’ than a P5 (perfect ﬁfth), nor-

mally perceived as very consonant.

Recent research suggests that the estimation of

the critical bandwidth proposed by Zwicker’s group

is too large. Other researchers, notably Green-

wood (Greenwood, 1961a) (Greenwood, 1961b), and

Moore & Glasberg (Moore et al., 1997), have pro-

posed different interpretations of the same phe-

nomenon. The term Equivalent Rectangular Band

(ERB) was introduced by them to avoid confu-

sion with the former notion of critical bands.

One expression to calculate ERB for frequencies

100≤ f ≤ 10,000Hz at moderate levels is

ERB( f) = 0.108f + 24.7, (1)

where ERB is in Hz and f is its center frequency

(Moore et al., 1997). Currently, this model is more

widely accepted.

Figure 2: Dissonance curve for an alto-trombone playing a

440Hz tone. The vertical lines indicate the ratios of Just-

Tuning temperament (JT).

3 PREVIOUS TECHNIQUES

Attempts to achieve perfect consonance have been

made since early stages of western music. In ﬁrst

approaches, keyboards were constructed with several

keys for the same note. This mechanism allowed

the performer to choose the most suitable pitch de-

pending on the context. One of the most impressive

achievements of this kind was the archicembalo of

Nicola Vicentino (Vicentino, 2006), who constructed

a keyboard capable of playing up to 36 pitches per

octave. His innovation, as well as many others like

it, never became popular due to the skills required to

play them.

3.1 MIDI-based Solutions

MIDI is a hardware and software speciﬁcation in-

tended to standarize communication among electronic

musical instruments (MIDI, 2001). By using both

MIDI and synthesizers, it is possible to overcome

the physical constraints of the tuning adaptability for

many instruments.

3.1.1 Springs Network

deLaubenfels (deLaubenfels, 2006) proposed a

method for minimizing dissonance in MIDI sequences

using Just-tuning (JT). In this method, musical

intervals are represented by a spring-network. The

accumulated energy of interconnected springs is ex-

pressed as the ‘pain,’ i.e., a dissonance measurement

of the sequence. Any elongation changes in the

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

springs affect in turn the net energy of the system.

By minimizing the total energy of the system, the

dissonance is presumed to be also minimized.

Three kinds of springs are used: vertical for simul-

taneous notes, horizontal to represent changes in pitch

of a note while sounding (or successively played), and

grounding springs to penalize the tuning drift of the

whole piece.

deLaubenfels’ program calculates the minimum

energy state of a sequence’s spring-network using

successive approximations produced by Monte Carlo

pseudo-random motion through the tuning space.

This algorithm re-tunes every note in the sequence un-

til zero net spring force is achieved for every interval.

3.1.2 Psycho-acoustical Curves

Sethares (Sethares, 2002b) uses the tonotopic theory

in Adaptun, a program to render more consonant

MIDI sequences in real-time. His algorithm grad-

ually decreases the precalculated dissonance of any

given chord by iteratively making small adjustments

in the pitch. The instrument spectrum for each MIDI

channel is known a priori; the calculation ignores the

amplitudes of the harmonics; a nominal frequency is

used to estimate the bandwidth for all the partials; and

the dissonance gradient is obtained by a variation of

Simultaneous Perturbation Stochastic Approximation

(SPSA).

SPSA is similar to simulated annealing in the way

that perturbation size is damped with every iteration,

but simulated annealing seeks global minima, while

SPSA seeks local minima (Spall, 1999). It uses only

two loss function evaluations per iteration, is tolerant

to noisy signals, and needs no information about the

gradient. The difference between the original SPSA

and the variation proposed by Sethares is that in the

latter, the damping coefﬁcients don’t vanish, allowing

his model to incorporate newly arriving notes.

In Adaptun, tonal drifting is prevented by means

of context, persistence, and memory models. These

mechanisms include absent partials in the dissonance

calculation which are somehow remembered by the

listener. Several musical examples processed with

Adaptun can be downloaded from (Sethares, 2002a).

3.1.3 MIDI Issues

The MIDI protocol speciﬁes three mechanisms to al-

ter the tuning of a single note: Bulk Tuning Dump

(non-realtime), Bulk Tuning Dump Request (non-

realtime), and Single-note Tuning Change (realtime.)

Although this last mechanism is the most suitable for

realtime implementations, it’s rarely found in contem-

porary synthesizers. To circumvent this problem, a

combination of pitch, pitch bend change, and pitch

bend sensitivity is commonly used to achieve the de-

sired frequency of a note. This mechanism is detailed

in (Villegas and Cohen, 2005).

There are several limitations to consider when us-

ing this combination: the pitch bend messages are ap-

plied to a MIDI channel, so the pitch bend value af-

fects all notes in a single channel, making it impossi-

ble to play a chord correctly. Also, if the release time

is long enough, the effect of a new pitch bend message

can be heard on the previous notes.

3.1.4 Observations Regarding Adaptun

Sethares’ program references the dissonance of each

timbre using a frequency of 500Hz. Instead of be-

ing calculated each time, these values are read from

memory easing the realtime implementation.

The use of a nominal frequency implies a uni-

form critical bandwidth across the auditory spectrum.

However, this is not the case. In Adaptun, the band

size error increases as the frequency increases or

decreases. Although Sethares’ implementation and

Helmholtz’s theory assume that the critical bandwidth

is independent of frequency, Plomp and Levelt have

emphasized the salience of the frequency in this cal-

culation.

4 PROPOSED MODEL

The purpose of the function to calculate tonal disso-

nance is to mimic the results obtained by Plomp and

Levelt. Even the value where the dissonance reaches

a maximum is described by them as “a rule of thumb”

(Plomp and Levelt, 1965).

Sethares formulated his model by a least-squares

ﬁt from Plomp and Levelt experimental data. Benson

(Benson, 2005) proposed an alternative expression

d(x) = 4|x|e

1−4|x|

, (2)

where x is the frequency difference as a fraction of

the critical bandwidth. This expression was adapted

to include ERBs, so for a dyad with amplitudes a

and

at frequencies f

and f

, dissonance is calculated

d(a

, a

, f

) = 2.5a

∆f

1−2.5

∆f

, (3)

where ∆f = | f

− f

| and bw = ERB(max( f

, f

)).

According to Plomp and Levelt, the dissonance

reaches a minimum value when the frequency differ-

ence is about one critical band. Beyond this interval,

LOCAL DISSONANCE MINIMIZATION IN REALTIME

dissonance decreases rapidly. A mechanism was in-

cluded in this open-form expression to avoid the dis-

sonance calculation when this condition is met:

d(a

, a

, f

) =











0if ∆ f > c bw;

2.5a

∆f

1−2.5

∆f

else;

(4)

where c is an arbitrary constant greater than unity.

The interaction of complex tones can be conve-

niently represented by matrices:







··· f







(5)







··· a







, (6)

with the successive frequency components of each

timbre listed in the rows of the timbre matrixT and

the amplitude of each frequency component listed in

matrixA. Both matrices are sized identically by the

numbers of timbres (m) and overtones (n). Based on

these matrices, the following expression is used to

calculate the dissonance of complex tones:

D =

m−1

∑

k=1

∑

j=k+1

∑

i=1

∑

h=1

d(a

, a

, f

). (7)

This equation calculates the sum of the dissonances

for each pair of frequency components belonging to

different instruments. It’s assumed that two consecu-

tive harmonics of a given timbre don’t fall within the

same ERB.

4.1 Implementation Considerations

4.1.1 Vicinity

The unison has the greatest consonance, and should

be passed through as the output as long as no other re-

strictions are imposed. In our algorithm, only vicini-

ties of the given inputs were considered, preserving

the character of the intervals. For example, if a duet

is playing an m3, the output of the algorithm is rec-

ognized as an m3 (minor third) and not an M3 (major

third), which in general has a lesser dissonance value

but different character.

On average, semitones are separated by 100 ¢.

The greatest discrepancy between 12-TET and JT is

about 16 ¢, occurring in the m3 and M6 (major sixth)

intervals. The pitch just noticeable difference (pitch

JND) is around 8.3 ¢ for the most acute region of the

human hearing spectrum, 1 kHz – 3 kHz (Loy, 2006).

Based on these values, a default vicinity of ±8¢ is

used for the application, but there are mechanisms

available that allow the user to adjust it. This default

value is large enough to potentially ‘correct’ a 12-TET

m3 without converting it into a different interval.

4.1.2 Computation Optimizations

The tonotopic theory asserts that frequencies whose

difference is greater than one critical band don’t con-

tribute to the dissonance of complex sounds. It’s pos-

sible to reduce the number of computations when cal-

culating dissonance using this fact: If the dissonance

equals zero when comparing a partial x of a timbre

against a partial y of another timbre, and x < y, then

the dissonance of each of the remaining partials of the

second timbre (ny with n > 1) and x will also be zero.

5 PD-BASED IMPLEMENTATION

Pure-data (Pd) (Puckette, 2006) is a realtime graph-

ical programming language for audio and graphical

processing. It was developed by M. Puckette and is

supported by an active community.

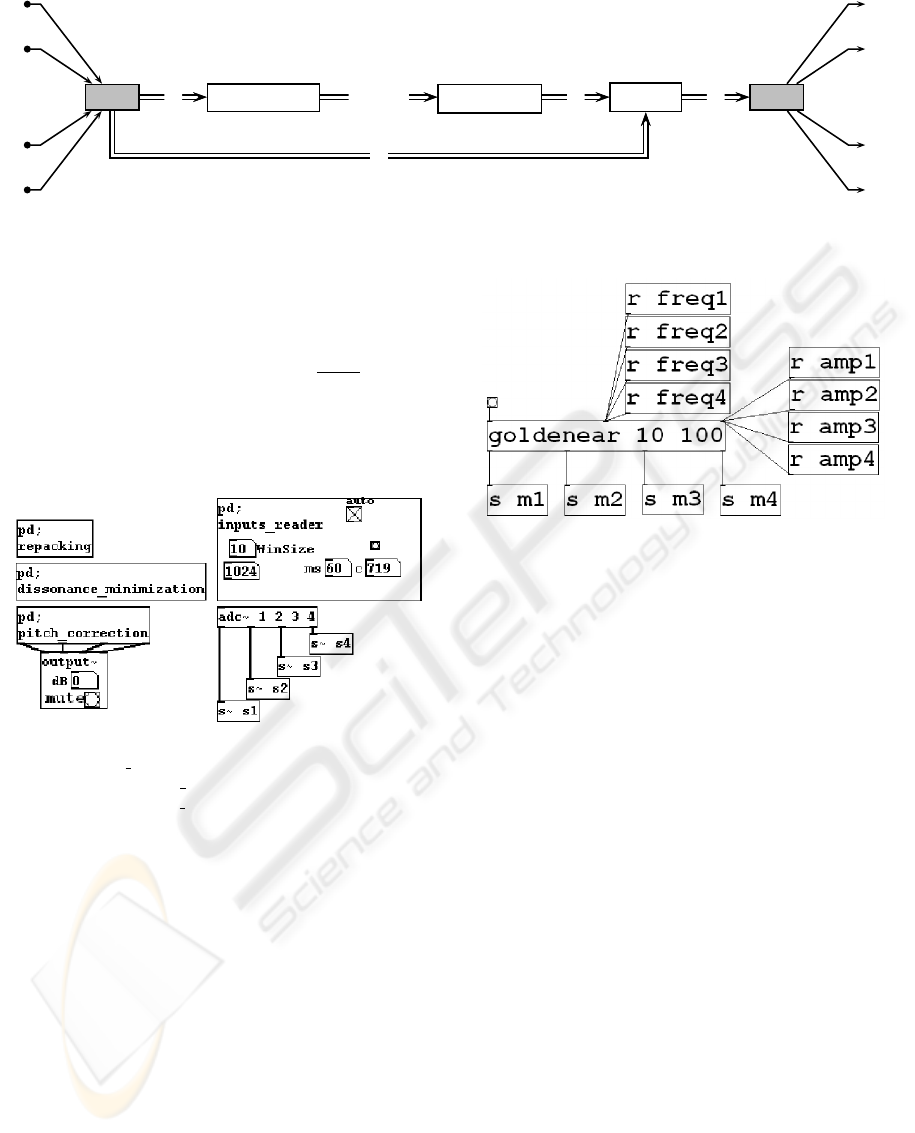
By means of one

adc˜

object, four analog signals

are converted into their digital equivalents. The ﬁrst

ten partials (fundamentals included) of each signal are

extracted using

fiddle˜

objects. The frequencies and

amplitudes are separated and passed to a

goldenear

object, which calculates target frequencies for each

signal. The pitch correction is performed by single-

sideband modulation (SSB) before ﬁnal conversion.

Figure3 shows the overall data ﬂow.

Fiddle˜

is a pitch detector. A list of spectral com-

ponents (frequency-amplitude pairs) used in the pitch

determination can be obtained from one of its outlets.

Fiddle˜

parameters and features are not addressed

here, but are explained in (M. Puckette et al., 1998).

Pitch correction is traditionally performed us-

ing vocoders which preserve the formants. Since

vocoders are time (and processor) consuming, SSB

was selected as a simpler but effective alternative.

SSB is a reﬁnement of AM in which one of the

two sidebands is eliminated. This mechanism works

as follows: An original signal x(n) is ﬁltered to obtain

a complex function X(n) which real part is equivalent

to x(n). The used ﬁlters implement the Hilbert trans-

formation. The resulting signal is then multiplied by

a complex sinusoid Y(n). The real part of this multi-

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

adc˜ fiddle˜

4 goldenear

SSB ×4

dac˜

digital

signals

frequency

components

4× 10× 2

∆f

digital

signals

Figure 3: Overall data ﬂow of the implemented solution.

Goldenear

was newly created for the purposes of this research.

plication has partials at the frequency components of

x(n) plus the frequency of Y(n). The resulting signal

can be expressed as

(n) = ℜ{X(n)Y(n)} = ℜ{X(n)e

(

±ı2πf

)

}, (8)

where f

is the frequency of the carrier Y(n) and f

the sampling frequency. Figure4 shows a screenshot

of GUI for the implemented patch.

Figure 4: Implemented GUI in Pd.

Fiddle˜

objects are in-

side the ‘

inputs reader

’ block,

goldenear˜

objects are

inside the ‘

dissonance minimization

’ block, and SSB

objects are in the ‘

pitch correction

’ block.

5.1 Goldenear

Goldenear

was created by the ﬁrst author to calculate

target frequencies in the vicinity of the fundamentals

of the input signals. In this Pd-object, the user can

specify the vicinity in ¢ and the maximum number

of iterations to evaluate the dissonance function, as

shown Figure 5.

When a new tone is detected, its amplitudes and

frequencies are sent to

goldenear

. A label is preﬁxed

to each frequency and amplitude list to distinguish be-

tween the signals. In the SPSA estimation, fundamen-

tal frequencies are modulated but the overtone ratios

are preserved. Also, since the frequency range of the

hearing spectrum is broad, the modulations are scaled

so they represent the same percentage of change for

each fundamental frequency.

Figure 5:

Goldenear

as connected in the implementation.

Practical and asymptotic expressions to calculate

the damping rates are provided in (Spall, 1998). How-

ever, the dissonance problem doesn’t ﬁt the canonical

form of SPSA, so in this research, these values were

selected by trial and error. SPSA delivers good ap-

proximations of the gradient (Spall, 1999). When the

algorithm fails in ﬁnding better tunings for the fun-

damentals, the original tones are passed through as

output.

The dissonance is calculated thrice for each SPSA

iteration: twice due to the intrinsics of SPSA and once

to monitor the partial solutions. If the dissonance falls

below a threshold, the current solution is selected and

the rest of the iterations are skipped. This extra evalu-

ation potentially saves some cycles in the dissonance

calculation.

5.2 Limitations

Our solution has several limitations: Tonal drift is not

explicitly prevented; there are times when the ERB

function is extrapolated; in the event of simultane-

ous signals, only one is analyzed due to the mono-

threaded nature of the application as imposed by Pd’s

paradigm; ﬁnally, sounds with long transients cannot

be processed adequately. Although polyphonic sig-

nals can be processed, best results are achieved when

monophonic signals are used because the algorithm

can detect the fundamentals more easily.

LOCAL DISSONANCE MINIMIZATION IN REALTIME

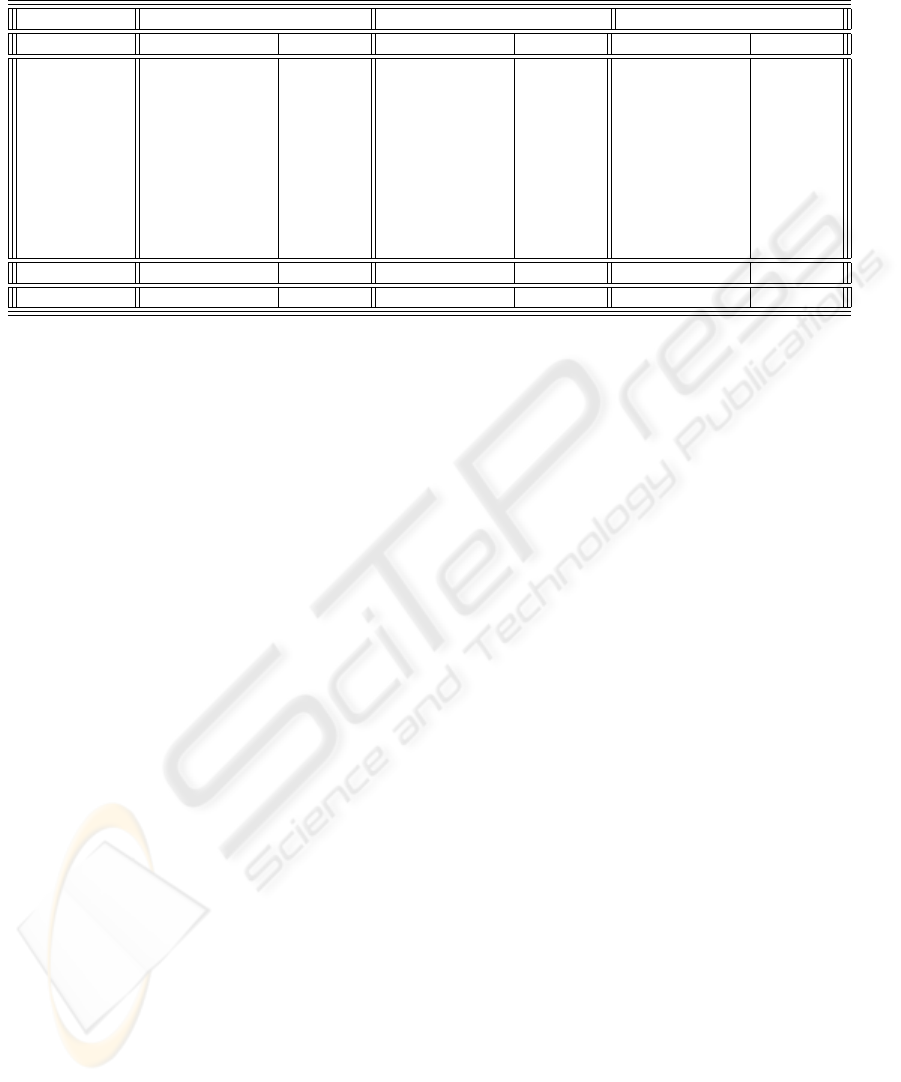
Table 1: Convergence results. Emboldened values indicate when the algorithm was unable to minimize the dissonance. The

initial dissonance was 8.42

Iterations 50 100 200

Trial ﬁnal dissonance time (ms) ﬁnal dissonance time (ms) ﬁnal dissonance time (ms)

1 5.25 4.8 4.9 9.56 5.64 18.69

2 7.12 4.61 6.59 9.64 3.49 18.91

3 7.57 4.85 8.9 9.42 3.49 18.62

4 7.46 4.82 6.78 9.51 3.43 18.87

5 8.14 4.58 6.28 9.29 5.79 20.44

6 8.63 4.8 4.29 9.65 3.48 20.22

7 5.72 4.83 4.59 9.59 4.67 18.89

8 7.56 4.78 6.8 9.55 3.29 18.98

9 8.45 4.82 8.94 9.46 6.18 18.66

10 7.32 4.81 6.28 9.61 4.29 18.92

Average 7.32 4.81 6.28 9.61 4.29 19.92

Std. Dev. (σ) 1.09 0.09 1.6 0.11 1.13 0.65

6 TESTS AND RESULTS

The platform for the tests comprised a Pentium

Xeon@2.79GHz with 1GB of RAM running MS

Windows XP, conﬁgured with an Edirol UA-101 au-

dio adapter using ASIO 2.0 drivers. The audio

was sampled at 48kHz, with an amplitude reso-

lution of 16 bits. The FFT analysis window was

1024 samples wide. Only monophonic signals were

presented as inputs. The signals were synthe-

sized versions of an alto-trombone extracted from

(Sandell, 1994). The Pd patches and audio ex-

amples for this research can be downloaded from

http://sonic.u-aizu.ac.jp/goldenear

6.1 Convergence Tests

For the convergence tests,

goldenear

was initialized

with a vicinity of 50 ¢ and fed four signals. The cho-

sen frequencies were intended to force the algorithm

to use a maximum number of iterations.

The elapsed time was measured using a Pd native

object. Final dissonances and elapsed time were mea-

sured after 50, 100, and 200 iterations. The results are

averaged and summarized in Table1. This data con-

ﬁrms that increasing the number of iterations lowers

dissonance levels. For 200 iterations, the dissonance

reduction was about 51 percent. The average time re-

quired for such a reduction was about 20 ms. When

fewer iterations were used, the algorithm occasion-

ally failed to ﬁnd better combinations of frequencies.

In those cases, the output was identical to the input.

6.2 Consonance Tests

Consonance tests were conducted to analyze the per-

formance of the algorithm presented with several

pairs of complex tones. The parameters were set at

a vicinity of 200 ¢ and a maximum of 200 iterations.

The frequencies were selected to fall within one crit-

ical bandwidth when the order of magnitude of the

fundamentals were comparable. It was also important

to ensure that at least one trial for each order of mag-

nitude was included.

There were two circumstances in which only one

evaluation was necessary for the algorithm: combi-

nations of frequencies in which no partials interacted

with each other, and comparison of a 3,500Hz tone

against itself. This fast calculation is a consequence

of the mechanism included to detect early conver-

gences. A similar reduction on iterations can be ob-

served in the interaction between frequencies of 4,000

and 4,100Hz. Table 2 summarizes the results.

7 CONCLUSIONS

A novel approach to generate a dissonance-minimized

version of concurrent sounds in real-time was pre-

sented. This method, based on the tonotopic conso-

nance theory, reduces the dissonance of sound sources

in real-time conserving their original character with-

out the use of a template. The proposed model works

best with harmonic sounds.

No subjective tests were conducted to validate the

results. However, they are in agreement with those of

other authors, and the convergence time of the algo-

rithm makes it adequate for practical applications like

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

Table 2: Consonance results for a vicinity of 200 ¢ and 200 iterations. Each entry presents the original dissonance, the ﬁnal

dissonance, and the number of iterations used. The emboldened results indicate when the algorithm was unable to ﬁnd a

solution.

(Hz) 50 250 500 3,500 4,100 8,000 10,000

2.43794 0.23803 0.02993 0 0 0 0

60 2.13064 0.14365 0.02990 0 0 0 0

200 200 200 1 1 1 1

0.13261 1.51361 0.99174 0 0 0 0

280 0.07437 0.36581 0.85732 0 0 0 0

200 200 200 1 1 1 1

0 0.43215 0.30562 0.04310 0.04429 0 0

600 0 0.09146 0.15989 0.01501 0.03633 0 0

1 200 200 200 200 1 1

0 0 0.00578 0.000924 0.110313 0.535633 0.44375

3,500 0 0 0.00610 0.000924 0.113752 0.128432 0.385192

1 1 1 1 200 200 200

0 0 0.01502 0.82770 1.46862 0.00727 0.02849

4,000 0 0 0.01794 0.11263 0.00870 0.00759 0.02978

1 1 200 200 65 1 200

0 0 0 0.14990 0.52446 1.67656 0.13377

8,300 0 0 0 0.14696 0.01318 0.03017 0.13113

1 1 1 200 200 200 200

0 0 0 0.40320 0.35031 0.55946 1.23280

11,000 0 0 0 0.40305 0.34235 0.50941 0.99666

1 1 1 200 200 200 200

harmonizing performances of multiple instruments

with different tunings, learning how to sing or play

instruments in tune, learning harmony and musical

scale theory, freeing instruments from tuning restric-

tion.

REFERENCES

Benson, D. (2005). Mathematics and Music, chapter 4.

Consonance and dissonance. Cambridge University

Press. ISBN 0-521-85387-7.

deLaubenfels, J. (2006). Studio j: John deLaubenfels’

basement project. Retrieved March 13, 2007 from

personalpages.bellsouth.net/j/d/jdelaub

E. Zwicker, G. Flottorp, and S. Stevens (1957). Critical

bandwidth in loudness summation. J. Acoustical So-

ciety of America 29 (5), pages 548–557.

Greenwood, D. (1961a). Auditory masking and the critical

band. J. Acoustical Society of America 33 (4), pages

484–502.

Greenwood, D. (1961b). Critical bandwidth and the fre-

quency coordinates of the basilar membrane. J.

Acoustical Society of America 33 (4), pages 1344–

1356.

Huron, D. (2006). Music cognition handbook: A dictio-

nary of concepts. Retrieved March 13, 2007 from

musiccog.ohio-state.edu/Resources/Handbook.

Loy, G. (2006). Musimathics, volume 1. MIT Press. ISBN 0-

262-12282-0.

M. Puckette, T. Apel, and D. Zicarelli (1998). Real-time

audio analysis tools for pd and msp. Proc. Int. Com-

puter Music Conf. Retrieved March 13, 2007 from

www.crca.ucsd.edu/

tapel/icmc98.pdf

MIDI, M. A. (2001). The Complete MIDI 1.0 Detailed

Speciﬁcation, chapter Section 2. MIDI Manufacturers

Association.

Moore, B., Glasberg, B., and Baer, T. (1997). A model

for the prediction of thresholds, loudness, and partial

loudness. J. Audio Engineering Society 45 (4), pages

224–40.

Plomp, R. and Levelt, W. (October 1965). Tonal conso-

nance and critical bandwidth. J. Acoustical Society of

America, pages 548–560. Volume 38, Issue 4.

Puckette, M. (2006). Software by Miller Puck-

ette. Retrieved March 13, 2007 from

www.crca.ucsd.edu/

msp/software.html

Sandell, G. J. (1994). SHARC - Sandell harmonic archive.

release 0.921.

Sethares, W. (2002a). Adaptun. Re-

trieved March 13, 2007 from

eceserv0.ece.wisc.edu/

sethares/adaptun

LOCAL DISSONANCE MINIMIZATION IN REALTIME

Sethares, W. (2002b). Real-time adaptive tunings using

Max. J. New Music Research Vol. 31 No. 1, pages

1–7.

Spall, J. C. (1998). An overview of the simulta-

neous perturbation method for efﬁcient optimiza-

tion. Johns Hopkins APL Technical Digest Vol. 19,

pages 482 – 492. Retrieved March 13, 2007 from

www.jhuapl.edu/SPSA/

Spall, J. C. (1999). Stochastic optimization: Stochastic

approximation and simulated annealing. Encyclope-

dia of Electrical and Electronics Engineering, pages

529– 542.

v. Helmholtz, H. (1954). On the Sensations of Tone as a

Physiological Basis for the Theory of Music, chapter

VIII, On the beats of simple tones. Dover Publica-

tions, ii english edition.

Vicentino, N. (2006). L’antica musica ridotta alla mod-

erna prattica. Retrieved March 13, 2007 from

visualiseur.bnf.fr

Villegas, J. and Cohen, M. (2005). Melodic stretching with

the Helical Keyboard. In Proc. 2

Int. Conf. on Enac-

tive Interfaces 2005. IST Network of Excellence EN-

ACTIVE.

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

100