FEATURES EXTRACTION FOR MUSIC NOTES RECOGNITION

USING HIDDEN MARKOV MODELS

Fco. Javier Salcedo, Jesús Díaz-Verdejo and José Carlos Segura

Department of Signal Theory, Telematics and Communications, Granada University, Spain

Keywords: Music information retrieval, Hidden Markov Models, music features extraction, music notes recognition.

Abstract: In recent years Hidden Markov Models (HMMs) have been successfully applied to human speech

recognition. The present article proves that this technique is also valid to detect musical characteristics, for

example: musical notes. However, any recognition system needs to get a suitable set of parameters, that is, a

reduced set of magnitudes that represent the outstanding aspects to classify an entity. This paper shows how

a suitable parameterisation and adequate HMMs topology make a robust recognition system of musical

notes. At the same time, the way to extract parameters can be used in other recognition technologies applied

to music.

1 INTRODUCTION

The music represents another way in human

communication. Instead of transmitting ideas like in

voice, they express (or they try to express) feelings

(Scheirer, E. D., 2000). At this moment, techniques

and systems of speech recognition are in a more

developed stage than its equivalents for music. The

reasons are simple: the complexity of the music

signal due to the variety of the possible sounds, and

its structure in several and simultaneous levels:

polyphony (De Pedro, D., 1992). That leads to

unsatisfactory results obtained by the recognition

systems when they are applied to music. On the

other hand, Hidden Markov Models (HMMs) have

shown good performances when applied to human

speech recognition, making them suitable for real

applications. We will show in this work that, with an

adequate parameterisation, and the incorporation of

information about the musical structure, HMMs can

also be successfully employed for music.

There are few specific works described in the

bibliography that make a study of the best-suited

parameters to characterize the musical signal. The

first studies tried to extract the pitch of the signal in

order to detect the music notes like Kashino’s

(Kashino, K., Murase, H., 1998) and Gómez’s works

(Gómez, E., Klapuri, A., Meudic, B., 2003). One of

the most outstanding is Beth Logan’s work (Logan,

B., 2000). She shows that cepstral coefficients are

appropriate for discriminating between music and

voice. She finally points out the need to accomplish

a deeper study about the quantity of coefficients

used, the sampling period, the size of the windows

and the perceptual scale, in order to model the music

efficiently. In another work, Durey and Clements,

use the HMMs to index music by melody (Durey,

A.S., Clements, M.A., 2001 and 2002). They make a

soft study to determine the best features to use for

music. This study is made using the FFT (Fast

Fourier Transform) coefficients, the Log Mel-scale

filter bank parameters and the MFCCs (Mel

Frequency Cepstral Coefficients). The best results

were obtained by MFCCs. Unfortunately Durey did

not justify other values used in the parameterisation,

like the size of the windows or the number of

coefficients chosen.

The present paper has a clear objective: to

determine a suitable parameterisation for musical

signals. The article begins (Section 2) with a simple

explanation about the musical notes and the basic

foundations of HMMs. Section 4 is devoted to some

basics of the HMMs (topology, training and

grammar) used in the recognition system. After that,

in Section 4 the database used to develop and test

the system is described, while Section 5 shows some

details of the implemented recognition system. From

this point, the sequence of experiments to determine

the best parameterisation is described. The system is

tested in two conditions: with pieces of music played

with one instrument (Section 6), and later with the

same pieces played with other different instruments

184

Javier Salcedo F., Díaz-Verdejo J. and Carlos Segura J. (2007).

FEATURES EXTRACTION FOR MUSIC NOTES RECOGNITION USING HIDDEN MARKOV MODELS.

In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 180-187

DOI: 10.5220/0002139301800187

 SciTePress

(Section 7). The results obtained by the proposed

recognition system are compared with those

provided by Durey’s system on the same database

when using the best parameters. Finally, the last

section offers conclusions.

2 THE MUSICAL NOTES

A musical note is completely characterized by four

values (Seguí, S., 1984):

1. Name: The name of the musical note determines

its height or frequency within the musical scale.

There are seven names for musical notes from A

to G.

2. Musical scale: The general scale of the sounds

includes all the range of sounds inside the limits

of identification for the human ear.

Approximately such limits are between 27 and

4750 Hz, which match with the lowest and the

highest note played by a concert piano,

respectively. The general scale is divided into

sets, named octaves. Each octave has a number

to indicate the position in the general scale,

which is called the acoustic index.

3. Alteration: The tone is the distance between two

notes without alteration. There are two

exceptions, the first one, between the E and F

notes and the second between the B and C notes

in the same scale. A note can be changed in one

of two directions:

• Sharp. The intonation of the affected sound

increases one semitone.

• Flat. Reduce one semitone the intonation of

the affected sound.

Therefore, the note name, its octave, and if there is a

change or not, determines the fundamental

frequency of the musical note.

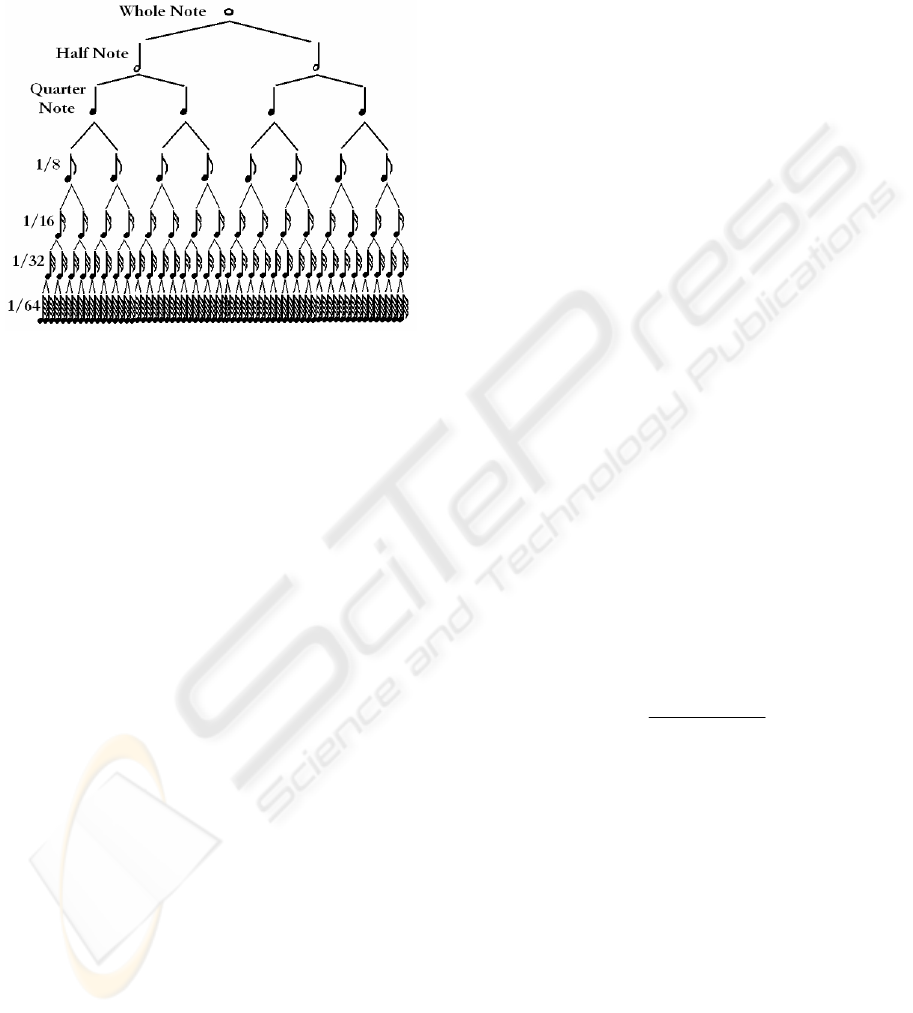
4. Duration: The duration of the notes are defined

in a relative way. The relation between two

adjacent notes duration is a half time. The

longest duration note is the whole note. The

next one is the half note which is played in a

half time of the whole note and so on. This

partition time process continues until it’s

obtained the shortest note, the sixty-fourth note

(Figure 1).

3 RECOGNITION SYSTEMS

BASED ON HMMS

These kinds of recognition systems are characterized

by the use of a production model, that is, by a

Hidden Markov Model. These production models

are estimated through a training phase, in which

enough patterns have to be offered to the system.

The recognition procedure can be described as

the calculation of the probabilities P(W|O) that an

observation O is produced by some model or

sequence of models W, on all the set of possible

models, in order to find the one that provides the

maximum value,

{P(W|O)}

|O)WP( max=

∧

(1)

Probabilities P(W|O) cannot be directly

evaluated, but they can be obtained using Bayes's

rule according to:

P(O)

P(O|W)P(W)

P(W|O)

⋅

(2)

where the

P(W) is the “a priori” probability of the

model or the sequence of models

W, P(O|W) is the

production probability to observe

O given the

sequence of models

W, and P(O) the probability that

the observation

O takes place. We can suppose P(O)

constant for a given input. Then, the task of

recognition implies finding the model, or the set of

models, that maximizes the product

P(W)·P(O|W)

instead of P(W|O). In this way, in our case, it is

necessary to consider two models: the acoustic

model, determined by

P(O|W), and the language

model, described by “a priori” probabilities P(W).

The acoustic model can be represented by using

Hidden Markov Models (Rabiner, L., Juang, B.,

Levinson, S., Sondhi, M., 1985), while the language

Figure 1: Relations between note durations.

FEATURES EXTRACTION FOR MUSIC NOTES RECOGNITION USING HIDDEN MARKOV MODELS

185

model can be modelled by a probabilistic finite state

automaton.

The recognition unit used is the note, which is

modelled through HMMs. This way, each HMM

will represent a single note, while the language

model or grammar contains information about valid

sequences of notes. This is possible through the

inclusion of a probability of such sequences.

The constituent elements of a Hidden Markov

Model are five (Rabiner, L., 1989):

1. A set of

N interconnected states, which must be

reachable from at least one state.

},...,s,s,s{sS

N321

(3)

2. A set of M observable symbols that can be

produced by HMMs.

},...,o,o,o{oO

M321

(4)

3. A matrix of transition probabilities between

states,

A={a

}. This is a square matrix of

dimension N. Each element a

corresponds to

the transition probability from the state

to the

state s

. The values of a

elements must be

between 0 and 1, due to its probabilistic nature.

Transition probabilities with the same origin

state must be normalized:

∑

(5)

4. A set of parameters

B={b

(k)} that define for

each state the probability density function of

productions. Assuming that

represents the

observation value at instant t, each b

can be

defined according to:

Ni) so|qP(x(o)b

itti

≤≤

(6)

5. A set of initial-state probabilities

P={π

}, where

is the probability that HMM starts on state s

Ni) sP(qπ

≤≤== 1

(7)

The initial-state transitions probabilities

should

verify:

∑

(8)

4 THE MUSIC DATABASE

One of the problems that arises in recognition

systems is how to offer enough well identified

samples to them. Thus, the database must contain

enough notes of each type in this case. On the other

hand, all the notes must be identified in the signal

correctly, that is, to set the name of the note played,

and the period of time that note appears on the

signal. This is called the labelling process. We have

chosen MIDI format because it offers the possibility

to generate note sequences and to label the musical

signal automatically. The process to make the

database is the following: the MIDI samples with

1000

2000

3000

4000

5000

6000

7000

8000

9000

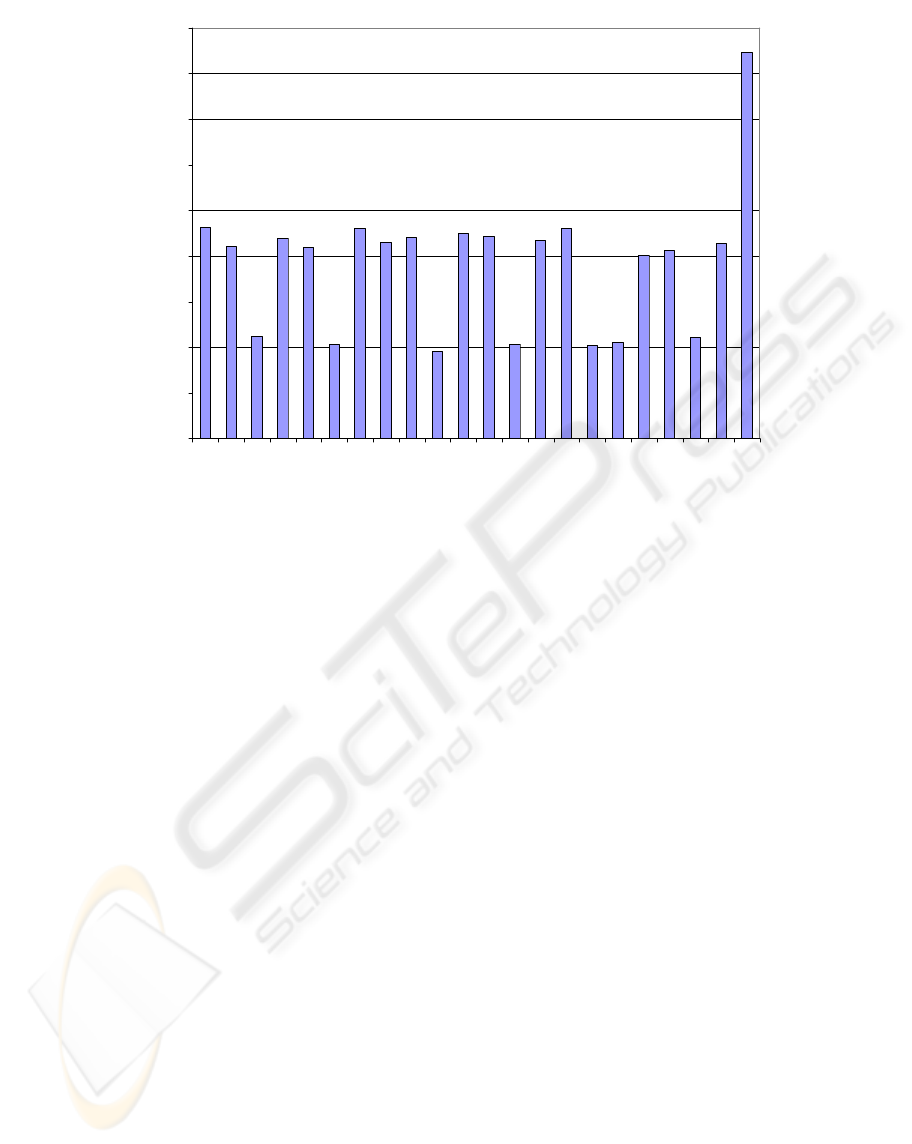
A3 B3 C3 D3 E3 F3 G3 A4 B4 C4 D4 E4 F4 G4 A5 B5 C5 D5 E5 F5 G5 sil

Appearance frequency

Figure 2: Statistical appearances of the notes in all the database samples.

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

186

aleatory note sequences are generated first, then they

are played and recorded using some instruments as

live music to obtain the database samples. The

recognition system is trained and tested using these

samples. Finally the labelling process is applied

using the information contained in the original MIDI

samples.

The database is made with 100 MIDI samples of

30 seconds. Each sample is a sequence of aleatory

notes and silences of the same duration (180 ms).

These MIDI samples have been recorded using five

instruments: piano, guitar, clarinet, organ and

vibraphone. Then 500 samples are obtained in single

channel wav format.

The signals have been generated in MIDI format

using aleatory notes. In this way, there is the same

probability for all the possible note sequences. This

fact lets the recognition system focus on the acoustic

model improvement, instead of the language model,

that will be affected using real music.

The musical notes from the samples belong to

the scales with index 3, 4 and 5, that is, attending to

its fundamental frequencies, from 132 to 1056 Hz.

There aren’t any altered notes (flats or sharps) in

database samples. Figure 2 shows the statistical

appearances of the notes and the silence in all the

samples of the database. It can be observed that

there are three different appearance frequencies.

This fact allows to know if the training stage is made

correctly, when there is no significant recognition

results between notes with different appearance

frequencies.

5 THE NOTES RECOGNITION

SYSTEM

Some parameters and properties of the recognition

system need to be established before exposing the

parameterisation study.

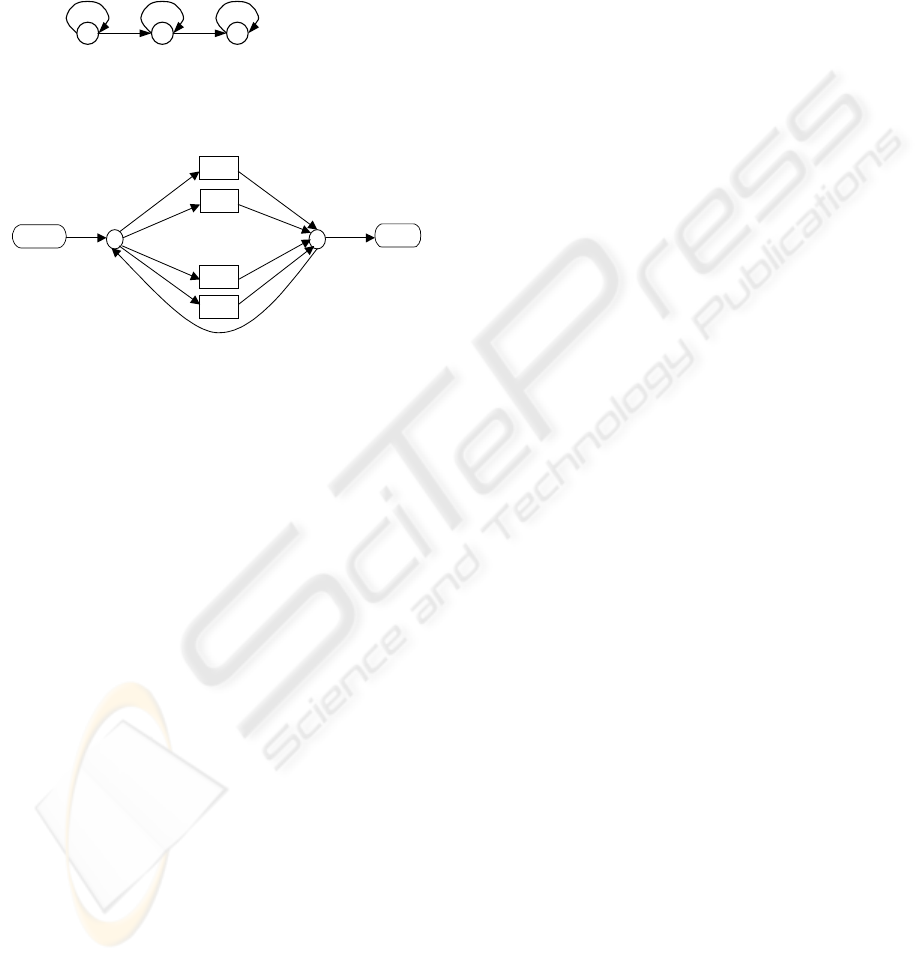
5.1 HMMs Topology

The temporary evolution of a musical note can be

split into three parts (Fletcher, N. H., Rossing, T. D.,

1991): the attack, sustain and relaxation zone. This

fact suggests using a HMM model for each note with

three states. Each of these states will model one of

the three zones of a musical note. The model is a

Bakis’s one, so there are only forward transitions

between one state and the next, and self-transitions

(Figure 3).

5.2 Grammar

The grammar, according to the sampled database,

consists in an undetermined succession of notes that

have the same probability of taking place in the

sequence. The notes that can appear in the musical

signal belong to scales 3, 4 and 5. Therefore there

are 21 different notes plus silence, which makes 22

symbols. Figure 4 shows the grammar used, which

allows transitions between all the notes and the

silence.

5.3 Training

The models are started by extracting all the

realizations of each note from the training set. For

this purpose it is necessary to consider the

segmentation derived from the labelling of the

recorded samples Later, Baum-Welch's algorithm

(Rabiner, L., 1989) is used for isolated training of

HMMs. The number of training iterations have been

adjusted to get differences below 10

-5

in log(P(O|λ))

between two successive training iterations.

In order to improve the statistical validity of the

results the Leave-one-out method has been used. We

have chosen 80% of the samples for training and the

other 20% for recognition purposes. This way 5

partitions of the database samples have been

established. In each experiment, 4 of them are used

for training and the last one for recognition.

1 2 3

States

Figure 3: HMMs topology to detect musical notes.

START

END

sil

. . .

Figure 4: Grammar used for note recognition. The initial

and final confluence points enable any sequence of notes

and silences.

FEATURES EXTRACTION FOR MUSIC NOTES RECOGNITION USING HIDDEN MARKOV MODELS

187

6 PARAMETERISATION

FOR UNIQUE INSTRUMENT

RECOGNITION

This experiment tries to obtain an initial

parameterisation for mono-instrumental recognition

conditions. For this reason the system is to train and

to evaluate using only the piano samples of the

database.

6.1 Initial Parameterisation

The initial parameterisation used is based on

Logan’s study (Logan, B., 2000) and the one used

by the authors on rhythm detection (Salcedo, F.J.,

Díaz, J.E., Segura, J.C., 2003). The way the features

are extracted is done in the following way:

1. The recordings were made at a sampling rate of

22050 Hz using a single channel.

2. Hamming windows are applied over the signal

to extract the features vectors. The windows

have a 15 ms size and are overlapped by 50% of

its size: 7.5 ms.

3. For each window the first 14 MFCCs (Mel

Frequency Cepstral Coefficients) and the energy

are calculated. The first and second order

coefficients are calculated too. This makes an

amount of 45 coefficients for each characteristic

vector.

4. Parameters have been extracted making an

energy normalization in the samples in order to

minimize undesirable effects caused by

different recording conditions.

6.2 Signal filtering

The signals to be used by the system must be filtered

according to a bandwidth. We have selected three

bandwidths to evaluate. These bandwidths

correspond to different configurations of complete

scales and the harmonic zone. Bearing in mind that

the musical notes of the samples belong to the scales

3, 4 and 5, the filtering bands to evaluate are the

following:

• The scales that belongs to the notes of the

samples, that is, from 128 to 1023 Hz.

• The scales 3, 4 and 5, and all the highest scales

including the harmonics zone to 8184 Hz.

• All the possible scales and the harmonic zone

from 64 to 8,184 Hz.

The filtering limits are calculated as the half-way

frequency between the last note of the previous scale

and the first one belonging to the following scale.

6.3 Number of Mel filters

Another parameter under consideration is the

number of Mel filters, that in all cases have been

taken equal to the number the notes present in the

filtering bandwidth, or in sequences like:

1k 1)1(2

≥−+=

−

(9)

where the F is the number of filters, and M is the

number of notes that exists in the considered

bandwidth. This way, the number of filters is

proportional to the number of musical notes of the

considered band.

Table 1: Recognition and error rates varying filter bandwidth and the number of filters in Mel scale (piano samples).

Filtering (Hz) Number of

filters

% correct

notes

% deleted

notes

% substituted

notes

% inserted

notes

Percent

Accuracy

64-8.184 49 97,66 0,60 1,74 1,20 96,46

128-8.184 35 98,73 0,67 0,60 1,28 97,45

128-8.184 71 97,49 0,59 1,92 0,98 96,51

128-1.023 21 98,77 1,22 0,01 1,54 97,23

128-1.023 43 99,02 0,95 0,03 1,73 97,30

128-1.023 87 99,17 0,82 0,01 1,09 98,08

128-1.023 175 99,12 0,82 0,07 1,76 97,37

Table 2: Comparison between Durey’s system and the best results obtained in the experiment with one instrument.

SYSTEM

% Correct

notes

% deleted

notes

% substituted

notes

% inserted

notes

Percent Accuracy

Durey 86,73 11,31 1,97 4,81 81,92

Best features

99,17 0,82 0,01 1,09 98,08

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

188

6.4 Results

Table 1 shows the different precision accuracies

(PAs) and error rates obtained by the system with

various filtering bandwidths and number of filters in

Mel scale. The best results are obtained applying the

bandwidth corresponding to the fundamental

frequencies of the notes, and by using 87 filters.

Thus the optimum number of filters is obtained from

expression (9) with

k=3.

This result is 16% better in precision accuracy

than that obtained by Durey’s system using the same

samples database (Table 2). The improvements

observed for the developed system are due not only

to the features extraction, but also by other aspects

like HMMs topology.

7 FEATURES FOR

MULTI-INSTRUMENTAL

NOTES RECOGNITION

This experiment is aimed at obtaining an improved

parameterisation for multi-instrumental notes

recognition.

This experiment is affected by a high number of

variables. Thus, in order to make the diagnosis

results easier, and to decrease the number of possible

combinations, it has been carried out in three stages:

• First: In this stage we try to determine the cut-

off filtering frequencies and the number of

filters applied in Mel scale. The variables in this

phase are the same as the ones used in the

previous experiment.

• Second: This stage attempts to find the number

of MFCC coefficients necessary to characterize

musical notes adequately.

• Third: It is the final stage in which the size of

the windows and their overlay are evaluated.

7.1 First Stage

Results are worse than those obtained in previous

experiments using the best parameterisation (Table

3). Now, the percentage accuracy has decreased to

77.02%, using the 128-1023Hz bandwidth, and 87

filters. The introduction of new instruments has

triggered the error rates, as we could expect.

Nevertheless, we can extract a conclusion from

the data shown in Table 3: the system obtains the

best results with bigger bandwidths, because the best

PAs of the series surpass 80%. Therefore it’s better

to use a method of filtering in which all the possible

scales and the harmonics zone are included, that is

the 64 to 8.184Hz bandwidth.

Insertion errors descend to the minimum value

using 99 filters, while deletion and substitution

errors are also one of the best from the table.

Therefore, the optimum filters number is the one

obtained from expression (9) with the value

k=2.

Comparing the best results obtained until now

with Durey's system evidences that the proposed

system improves by 10% the accuracy rate.

Nevertheless, we observe less success in detecting

notes, because substitution errors are greater than in

Durey’s one.

7.2 Second Stage

This phase is aimed at knowing how many MFCC

coefficients are needed in order to get more

information from the music signal.

At first sight, the results exposed in Table 4 have

higher PA (10%) than those obtained in the previous

stage. On the other hand, substitution errors decrease

appreciably when the coefficient number is higher.

The rest of the error rates are around the same levels,

and even increase a little. We can see a saturation for

the accuracy rate when up to 35 coefficients are

used.

Table 3: Recognition and error rates varying filter bandwidth and the number of filters in Mel scale. The notes of the

samples are interpreted by various instruments.

Filtering (Hz) Number of

filters

% correct

notes

% deleted

notes

% substituted

notes

% inserted

notes

Percent

Accuracy

128-1.023 21 83,25 2,10 14,65 7,08 76,18

128-1.023 43 85,15 2,32 12,53 5,45 79,70

128-1.023 87 82,80 2,73 14,47 5,79 77,02

128-8.184 35 82,03 1,41 16,56 12,37 69,66

128-8.184 71 82,67 1,47 15,86 6,55 76,13

128-8.184 143 81,97 1,61 16,42 5,67 76,30

64-8.184 49 84,82 1,77 13,41 4,05 80,77

64-8.184 99 85,16 1,96 12,88 3,79 81,37

FEATURES EXTRACTION FOR MUSIC NOTES RECOGNITION USING HIDDEN MARKOV MODELS

189

Although at this point there are more indications to

use 35 MFCCs to characterize the music signal, we

chose 40 for two reasons:

1. To make sure that the parameterisation of the

system is within the saturation zone of

information provided by the MFCCs.

2. Although this number of coefficients doesn’t

provide the best accuracy rate, it is the one that

gets minor substitution errors. This kind of error

goes down significantly by increasing the

MFCCs number.

7.3 Third Stage

It’s possible that the high insertion rates of the

system at this point, could be given by the different

temporary evolution of the notes played with

different instruments. This fact motivates the

following system tests, which consists of using

several window sizes with some different overlays

between them.

The window sizes used in the experiment

oscillate between 30 and 90 ms with overlays

between 50 and 80% of the window size.

Table 5 shows the experimental results. The

optimum point is produced using 60 ms windows

displaced by 12 ms. On the other hand, the

successful outcome of the results confirms the

validity of the HMMs topology for notes

recognition.

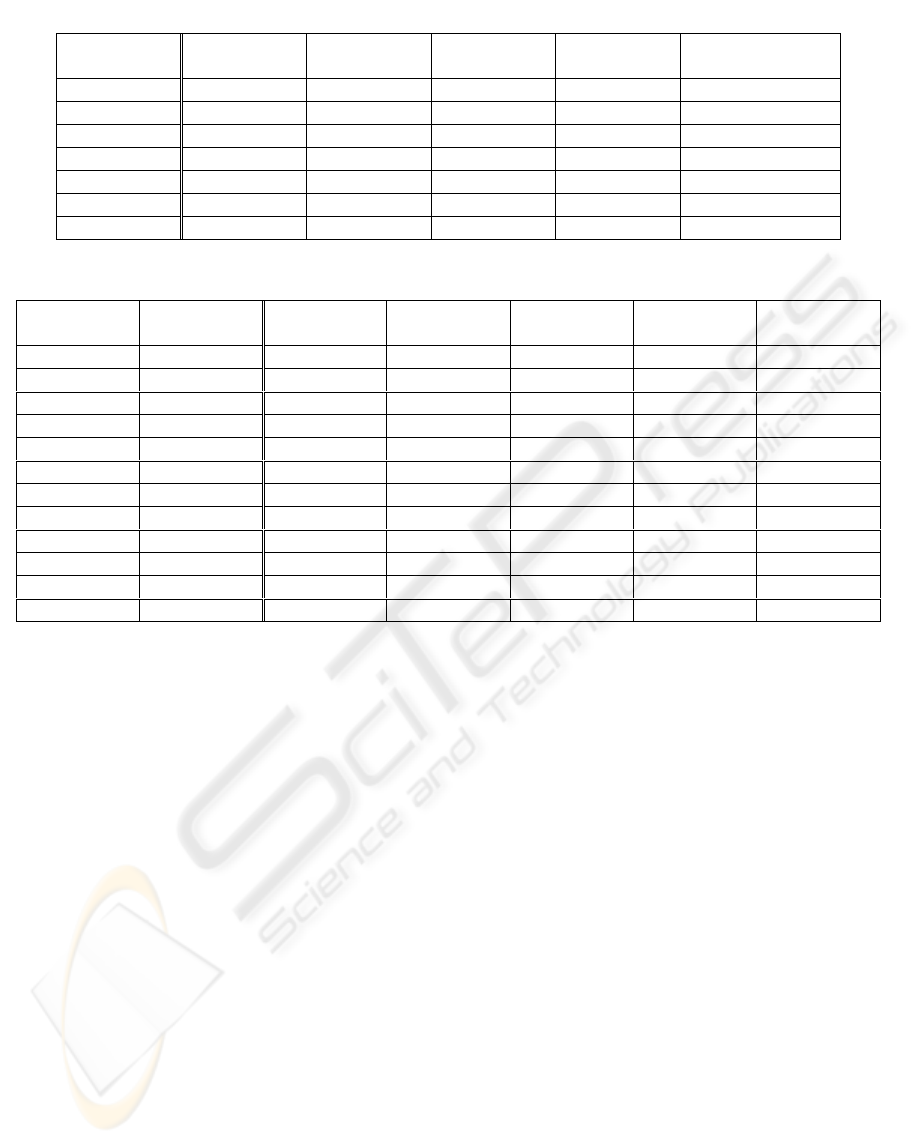
Figure 5 represents the percentage accuracy

evolution of the recognition system through the

successive parameterisation improvements made in

experiments.

Finally, we have to point out that accuracy rate

obtained by Durey’s system is 71.7% in multi-

instrument recognition conditions. This value is

lower than any one obtained by the proposed system

in any experiment in all the three stages (Table 5).

8 CONCLUSIONS

The present work shows a study on a suitable set of

features extracted from the signal to be used in

musical notes recognition. Likewise, Hidden

Markov Models have been shown to be powerful

enough when applied to musical notes recognition.

Table 4: Recognition and error rates varying the number of MFCCs.

Number of

MFCCs

% correct

notes

% deleted

notes

% substituted

notes

% inserted

notes

Percent Accuracy

14 85,16 1,96 12,88 3,79 81,37

20 92,49 1,75 5,77 4,29 88,19

25 95,14 1,50 3,36 4,66 90,48

30 96,72 1,70 1,58 4,73 91,99

35 97,39 1,97 0,64 4,93 92,46

40 97,43 2,10 0,46 5,84 91,60

45 97,27 2,18 0,55 6,05 91,22

Table 5: Recognition and error rates varying the windows width and its overlapping.

Window

Width (ms)

Overlapping

(ms)

% correct

notes

% deleted

notes

% substituted

notes

% inserted

notes

Percent

Accuracy

30 6 98,23 1,55 0,22 4,95 93,28

30 7,5 98,29 1,54 0,17 6,86 91,43

30 10 98,16 1,62 0,22 8,31 89,85

30 15 96,49 3,12 0,39 3,59 92,97

60 12 98,43 1,25 0,32 0,17 98,26

60 15 98,11 1,65 0,24 0,05 98,06

60 20 97,16 2,61 0,23 0,01 97,15

60 30 95,94 3,63 0,42 0 95,95

90 18 97,90 1,91 0,19 0,04 97,86

90 22 97,10 2,65 0,25 0 97,10

90 30 96,10 3,61 0,30 0,01 96,08

90 45 94,14 5,49 0,37 0 94,14

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

190

A suitable parameterisation and adequate models

have led to a robust basic recognition of musical

notes in cases of multi-instrumental recognition

conditions.

Finally, it is necessary to point out that the

parameterisation obtained can be used in other

recognition technologies.

REFERENCES

De Pedro, D., 1992. Teoría Completa de la Música.

Editorial Real Musical.

Durey, A.S., Clements, M.A., 2001. Melody Spotting

Using Hidden Markov Models. In Proceedings of

ISMIR 2001, International Symposium on Music

Information Retrieval.

Durey, A.S., Clements, M.A., 2002. Features for Melody

Spotting Using Hidden Markov Models. In

Proceedings of ICASSP 2002, International

Conference of Acoustic Signal and Speech Processing.

Fletcher, N. H., Rossing, T. D., 1991. The Physics of

Musical Instruments. Springer-Verlag, New York,

1991.

Logan, B., 2000. Mel Frequency Cepstral Coefficients for

Music Modelling. In Proceedings of ISMIR 2000,

International Symposium on Music Information

Retrieval.

Kashino, K., Murase, H., 1998. Music Recognition Using

Note Transition Context. In Proceedings ICASSP, pp.

VI 3593–6.

Gómez, E., Klapuri, A., Meudic, B., 2003. Melody

Description and Extraction in the Context of Music

Content Processing. Journal of New Music Research.

Volume 32, Number 1, March 2003.

Rabiner, L., Juang, B., Levinson, S., Sondhi, M., 1985.

Recognition of Isolated Digits Using Hidden Markov

Models with Continuous Mixture Densities. AT&T

Tech Journal.

Rabiner, L., 1989. A Tutorial on Hidden Markov Models

and Selected Applications in Speech Recognition.

Proceedings of the IEEE 1989.

Salcedo, F.J., Díaz, J.E., Segura, J.C., 2003. Musical Style

Recognition by Detection of Compass. In Proceedings

of IBPRIA 2003 Iberian Conference on Pattern

Recognition and Image Analysis.

Scheirer, E. D., 2000. Music-Listening Systems. Doctoral

thesis, Massachusetts Institute of Technology.

Seguí, S., 1984. Curso de Solfeo. Editorial Unión Musical

Española.

100

One

instrument

64-8184Hz

filtering

More filters More MFCCs 60ms

windows

Percent Accuracy (%)

Figure 5: Percent accuracy evolution of the system from the initial parameterisation to the last stage.

Table 6: Comparison between Durey’s system and the best results obtained in the experiment with multiple instruments.

SYSTEM % Correct

notes

% deleted

notes

% substituted

notes

% inserted

notes

Percent Accuracy

Durey 81,71 10,71 7,57 10,01 71,70

Best features 98,11 1,65 0,24 0,05 98,06

FEATURES EXTRACTION FOR MUSIC NOTES RECOGNITION USING HIDDEN MARKOV MODELS

191