SEARCHING FOR A ROBUST MFCC-BASED

PARAMETERIZATION FOR ASR APPLICATION

J. V. Psutka, Luboš Šmídl and Aleš Pražák

Department of Cybernetics, University of West Bohemia, Pilsen, Czech Republic

Keywords: MFCC parameterization, critical band-pass filters, robust front-end.

Abstract: The paper concerns with searching for areas of robust setting a MFCC-based parameterization as regards

numbers of band-pass filters and computed coefficients. Settings that are theoretically recommended for

telephone and microphone speech are compared with a large number of experimental results and a new

technique for determination of robust areas of {<# of band-pass filters>×<# of coefficients>} is designed.

1 INTRODUCTION

The state of the art parameterization techniques used

in ASR systems try to model the process of human

hearing. In speech processing terminology these

techniques are known as MFCC (Zheng and Song,

2001) and PLP parameterizations. It is well known

that both these techniques attempt to accommodate

the parameter estimation process to the way of

human hearing and how human perceive sounds

with various frequencies. However, one question

that we have to deal with is a selection of an

"optimal" number of critical band-pass filters and a

number of computed coefficients. In papers

published in many prestige world conferences we

usually find nearly always the same settings without

necessary analysis of the task conditions and

reference e.g. to the used sampling frequency of

speech signal (perhaps it is influenced by the default

setting the software tool HTK, which is frequently

used at many research labs). On the other hand, from

the relatively rich experience of building many ASR

systems we known that there isn't only one universal

setting which would yield for given "quality" of

speech signal the most successful results of

recognition experiments. Experimental results

however indicate that the best classification results

create in the space {<number of band-pass filters> ×

<number of coefficients>} certain areas in which the

successfulness is high and it doesn't change too

much (i.e. it doesn't dependent on the change of the

number of critical band-filters and the number of

coefficients). The goal of described works is to find

settings (i.e. the number of filters and derived

coefficients), which correspond to the best

recognition results and then for such solutions to

specify "areas of robust setting".

The whole work is done with the MFCC

parameterization and for speech data of telephone

=8 kHz) and microphone (F

=44.1 kHz) quality.

2 MFCC BASED PROCESSING

The computational algorithm of the MFCC

parameterization is realized by the bank of

symmetric overlapping triangular filters spaced

linearly in a mel-frequency axis, according to

auditory perceptual considerations. The spacing as

well as bandwidth of the particular filters is

determined by a critical-band concept. To execute

this process we have to perform following steps:

•Computation of short-term speech spectrum.

•Non-linear frequency transformation and critical-

band spectral resolution – triangular band-pass

filters in a mel-frequency axis.

Table 1: Recommended numbers of filters for different

values of sampling frequency.

• Computation of cepstral coefficients.

• Applying an inverse discrete Fourier transform.

Sampling

frequency

[kHz]

Band

width

[kHz]

Band

width

[mell]

Number

of filters

8 0÷4 0÷2146 15

16 0÷8 0÷2840 20

44.1 0÷22 0÷3921 27

196

V. Psutka J., Šmídl L. and Pražák A. (2007).

SEARCHING FOR A ROBUST MFCC-BASED PARAMETERIZATION FOR ASR APPLICATION.

In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 192-195

DOI: 10.5220/0002140401920195

 SciTePress

cul

,,Max,,

max

><><

,argmax

Max

cul

Max

>< c,c

c,c,f

For the final acoustic modelling we extended the

original MFCC representation with derived delta

and delta-delta features. See Table 1 for

recommended numbers of filters based on a

critical-band concept for different values of

sampling frequency.

3 SEARCHING FOR ROBUST

AREAS

We suggested following approach to the

determination of areas of robust parameter settings:

Searching for lower boundary of the number of

band-pass filters.

To find the lower boundary of a

robust area, i.e. left from the point of view a

minimum number of applied band-pass filters (see

Table 2 and 3), we chose such a statistic which

calculates for each number of band-pass filters the

average of the 5 best recognition results (

Acc)

obtained for different number of coefficients. Let us

define the recognition accuracy for

f band-pass

filters and

c coefficients as A

f,c

. Then to determine

the average value of the 5 best recognition results for

given number of band-pass filters we have to order

firstly results

f,c

according to the size, i.e. we define

f,[i]

, where A

f,[1]

≥ A

f,[2]

≥ .... and then we compute

desired statistic as

][,

∑

(1)

Now we find the maximum of for

f0< f

min

, f

max

where

min

is minimum and f

max

maximum values of

the number of band-pass filters, for which

measurements were performed, i.e.

(2)

The lower boundary of the robust area (from the

point of view applied band-pass filters) we can

define so that we determine the first (for increasing

number of filters) value of the number of filters

Lbou ,

for which the value is greater or equal than 99%

of , so

.argmin

5,Max5,

99.0

Lbou AA

≥

(3)

Determining lower and upper boundaries of a

number of coefficients.

Considering that the

recognition results don’t vary too much for

increasing number of band-pass filters and a fixed

number of used coefficients it is possible to derive

the lower and upper boundary of robust area for the

whole set of recognition results. A detail analysis of

all results (in Table 2 and 3 we could show – owing

to limited space – the results of only a small segment

of nearly one thousand performed experiments)

indicates that the area of the “best” results shifts

slightly towards higher number of coefficients. For

that reason the robust area was looked for as the

interval <

, f

> = <f

Lbou

, f

Lbou+9

>; <f

Lbou+10

, f

Lbou+19

A block of 10 band-pass filters was chosen so that

the resulting area might contain sufficient number of

measurements and calculated statistics could be

considered to be evidential (Freund,1998). For

individual values of a number of coefficients

c0<c

min

, c

max

> (where c

min

and c

max

are respectively

values of minimum and maximum number of

coefficients for which measurements were

performed) we determined average values

<l,u>,c

(in

intervals <

, f

(4)

Now we can define

<l,u>, Max

(5)

and then to determine the value of a number of

coefficients for which this maximum occurred

(6)

where

c0<c

min

, c

max

>. Now we can define the lower

<l,u>

and upper c

<l,u>

boundary of the robust

setting from the point of view a number of

coefficients. The desired interval was defined by the

values which don’t fall below 99% of

<l,u>,c

(7)

(8)

For this area we can define the value as the

number of filters for which attains its

maximum (i.e. its “optimum” or rather “reco-

mmended” value of a number of band-pass filters)

for <

, f

>. Now we can define

(9)

(10)

The area of robust setting. From the above

recommendations we can now determine the area of

robust setting of the number of band-pass filters and

coefficients as

robust area = (11)

The mean and deviation computed from recognition

results in this area give us a measure of quality for

given settings.

5,f

5,Max

5,f

>∈<=

><><

ccf

fffAA ,,max

ULUL

,,, Max,

>∈<=

ccf

fffAf ,,argmax

Max

,Max,

.max

5,5,Max f

AA =

><∈

+−

∑

maxmin,

cccA

cul

,argmin

Max,,,,

99.0

><><

≥

ulcul

cul

,argmax

Max,,,,

99.0

><><

≥

ulcul

cul

},,{

><∈×><∈

><>< ululul

cccfff

SEARCHING FOR A ROBUST MFCC-BASED PARAMETERIZATION FOR ASR APPLICATION

197

5Max,

4 EXPERIMENTAL RESULTS

As was presented above, all experiments were

performed using speech data sets of two different

qualities: telephone and microphone. The

telephone-based corpus consists of Czech read

speech transmitted over a telephone channel. One

hundred speakers were asked to read various sets of

40 sentences. The

microphone-based corpus (high-

quality speech) is a read-speech database consisting

of speech of 100 speakers. Each speaker read a set of

40 sentences (same as in the telephone-based case).

The telephone and microphone test sets consisted of

100 sentences randomly selected from utterances of

100 different speakers who were not included in the

training databases. The vocabulary in all our test

tasks contained 528 different words. There were no

OOV words. The basic speech unit of our system is

a triphone. Each individual triphone is represented

by a three states HMM; each state has 8 mixtures of

multivariate Gaussians. In all recognition

experiments a language model based on zerograms

was applied. For that reason the perplexity of the

task was 528.

MFCC parameterization with telephone data

To find areas of robust settings we systematically

built and tested nearly one thousand ASR systems.

In fact it was for f0<8,45> and c0<4,30>.

Recognition results of these experiments are

summarized in Table 2 and depicted in Figure 1 (for

lack of space Table 2 shows only a part of these

results).

cc [%]

Number of

filters

Number of static

coefficients

Figure 1: MFCC telephone-quality data.

Figure 2 shows the dependency of the average of the

5 best results on the number of band-pass filters. The

frequency for which the

5,f

A exceeds 0.99

5Max,

A is

Lbou

=14. In Table 4 you can find all important

statistics needed to determine areas of robust

settings. It is evident that from the point of view the

number of band-pass filters the first area begins by

crossing boundary f

Lbou

. An increasing number of

applied band-pass filters above this boundary has

practically no influence to the recognition accuracy.

8 13 18 23 28 33 38 43

Max,5

umbe

of filters

f,5

[%]

0,99A

Max,5

Figure 2: Dependency of

5,f

A on the number of filters.

The robust area f0<12, 21>×c0<10,14> and the

recommended setting f =15 and c=12 are in a very

good agreement with theoretically derived value

(M=15) enumerated in Table 1. Also the default

HTK setting (i.e. 13 coefficients) can be considered

to be correct even though a smaller number

coefficients (c0<10, 14>) is also appropriate.

MFCC parameterization with microphone data

The area of robust setting for microphone data was

searched in fact for f0<18,45> and c0<4,30>.

Results of recognition experiments are summarized

in Table 3 and depicted in Figure 3.

umber of static

coefficients

Acc [%]

Number of

filters

Figure 3: MFCC microphone-quality data.

Figure 4 shows that for microphone speech the value

exceeds 0.99 for f

Lbou

=25. Similarly as in a case

of telephone speech the recognition accuracy

changes for increasing number of band-pass filters

only slightly. However the area of robust setting is

here broader, c0<14,23>.

umber of filters

f,5

[%]

88,0

89,0

90,0

91,0

18 23 28 33 38 43

0,99

Max,5

Figure 4: Dependency of

5,f

A on the number of filters.

Let us note that this interval doesn’t contain the

HTK default setting, i.e. the value of 13 coefficients.

The robust area f0<22,31>×c0<14,23> and the

recommended setting f=29 and c=17 are again in a

relatively good agreement with theoretically derived

value (M=27) given in Table 1.The mean and

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

198

deviation computed from recognition results in this

area give us a measure of quality for given settings.

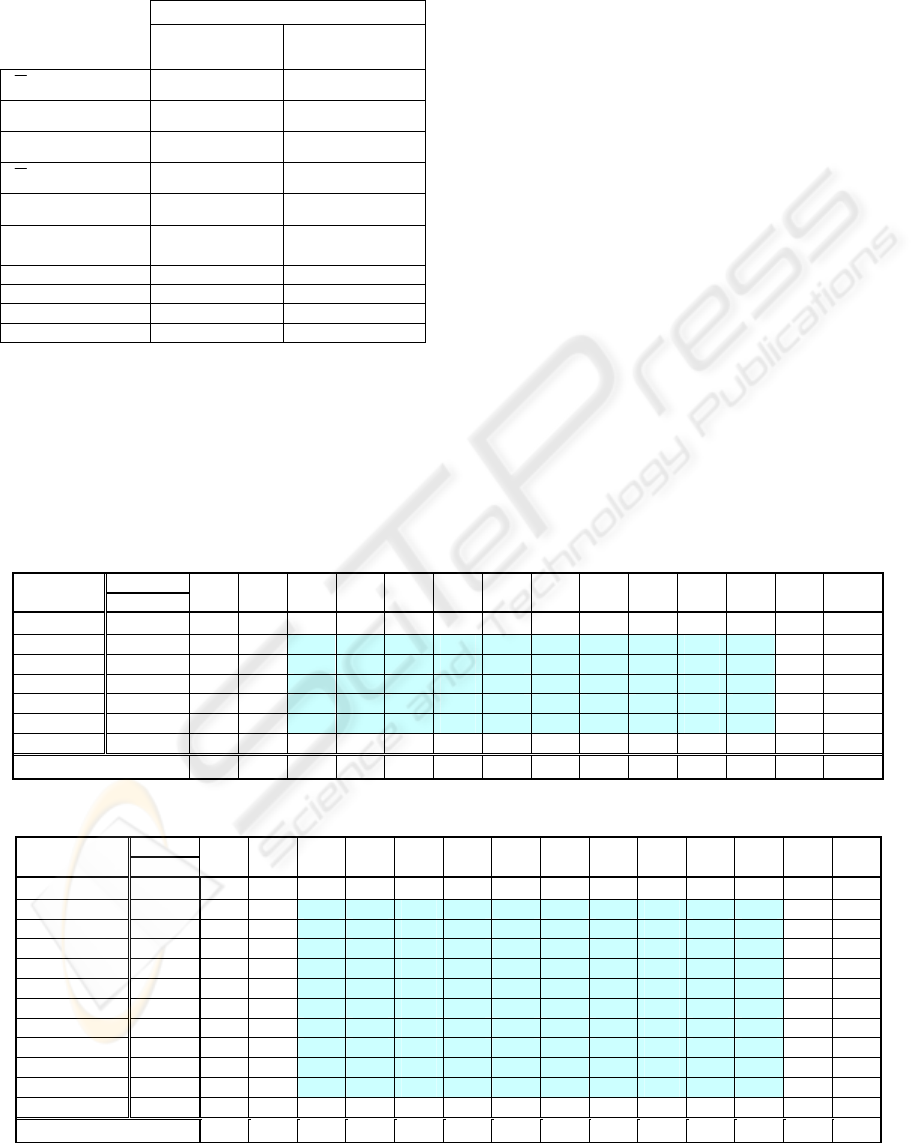
Table 4: Statistics for telephone/microphone data.

f 0 < f

, f

l=12, u=21

(telephone)

l=22, u=31

(microphone)

[%]

Max,u,l

84,60 89,73

Max

>< u,l

12 17

>< ul

10 / 14 14 / 23

[%]

Max, >< c,c

84,83 89,62

Max

>< c

15 29

Robust area

f 0<12,21>×

× c 0<10, 14>

f 0<22,31>×

× c0<14,23>

Recomm. setting f =15; c=12 f =29; c=17

# of measures 50 100

Average of Acc 84,24 89,40

Deviation of Acc 0,76 0,53

5 CONCLUSIONS

The MFCC-based parameterization is a very

efficient tool for description of speech in ASR

systems. We showed that the theory of critical-bands

of hearing is both for telephone (F

=8kHz) and

microphone (F

=44.1kHz) speech data in a good

agreement with experimental results. Very useful

conclusions were obtained for the numbers of

"robust" coefficients for which the ASR system

demonstrates comparable recognition accuracy.

ACKNOWLEDGEMENTS

This paper was supported by the AVCR, project no.

1QS101470516 and the project of the EU 6

FP no.

IST-034434.

REFERENCES

Fang Zheng, Guoliang Zhang and Zhanjiang Song,

Comparison of Different Implementations of MFCC,

J. Computer Science & Technology, 16(6): Sept. 2001.

Freund, J.E., "Modern elementary statistics", Prentice-

Hall, Englewood Cliffs, New Jersey 07632, 1988.

Psutka, J., Müller, L., Psutka, J.V., "Comparison of MFCC

and PLP Parameterization in the Speaker Independent

Continuous Speech Recognition Task",

EUROSPEECH'2001, Aalborg, 2001.

Table 2: Recognition accuracy for various numbers of filters and parameters for telephone data.

# filters

Average for

0<12

21>

# coeff.

10 11 12 13 14 15 16 17 18 19 20 21 22 23

83,12

83,98 82,95 83,76 83,10 83,76 83,25 83,32 82,88 82,81 82,95 81,93 83,39 82,15 82,07

84,01

13 83

47 85

67 84

50 84

86 83

91 83

10 85

01 83

84 83

10 83

54 83

32 82

81 82

84,25

84 83

61 84

42 84

13 84

42 84

20 84

42 84

86 83

76 83

91 84

20 84

28 83

84,60

17 83

10 83

32 84

79 84

42 85

75 84

35 84

28 85

16 85

01 84

86 84

06 82

95 83

84,47

78 82

22 85

82 83

91 85

08 85

45 84

72 83

98 82

88 83

47 84

57 85

30 84

42 84

83,86

50 81

63 81

85 84

42 84

64 84

86 83

91 83

54 82

59 83

84 84

35 84

64 84

28 83

83,46

53 80

68 81

78 81

56 85

16 84

57 83

32 83

69 82

22 83

84 84

50 83

91 83

76 84

Average of the 5 83,45 83,16 84,34 84,35 84,83 84,91 84,50 84,38 83,69 84,07 84,50 84,42 84,07 83,95

Table 3: Recognition accuracy for various numbers of filters and parameters for microphone data.

# filters

Average for

0<22

31>

# coeff.

20 21 22 23 24 25 26 27 28 29 30 31 32 33

88,62

87,51 89,29 88,15 86,72 87,08 87,79 88,51 89,94 89,65 89,65 89,36 89,36 89,65 89,22

89,34

72 88

87 88

65 89

44 90

01 89

08 89

51 89

58 89

44 89

42 89

44 89

52 89

89,36

01 88

94 89

29 88

08 89

01 89

44 89

51 90

22 89

36 89

22 89

65 89

86 89

51 89

89,60

94 89

72 89

72 90

15 89

65 89

08 89

36 89

51 89

36 89

35 90

01 89

79 90

22 89

89,73

87 89

22 90

08 89

58 89

44 90

01 89

58 89

94 89

58 89

88 89

36 89

86 90

29 89

89,67

15 89

08 89

02 89

68 89

36 89

31 89

44 89

88 89

58 90

51 89

94 89

51 89

89,58

65 88

87 90

08 89

36 89

58 89

36 88

87 89

41 89

86 90

01 89

94 89

36 90

36 89

89,43

72 89

65 89

29 90

08 88

87 90

29 89

86 89

44 89

01 88

29 90

08 89

79 90

89,39

94 89

58 89

15 88

94 88

87 89

65 89

22 89

35 90

15 90

01 89

35 89

22 90

08 89

89,19

51 86

37 88

44 89

72 89

22 89

58 89

51 88

72 89

22 89

79 88

94 88

79 90

22 89

89,40

08 86

80 87

22 89

86 91

22 89

79 88

87 89

94 89

72 88

94 89

22 88

94 90

88,78

94 87

15 86

94 89

94 88

37 88

65 89

79 88

72 89

29 89

22 88

65 88

22 88

51 89

Average of the 5 best

9 89

39 89

69 89

95 89

87 89

88 89

78 89

97 89

75 90

04 89

94 89

78 90

23 89

SEARCHING FOR A ROBUST MFCC-BASED PARAMETERIZATION FOR ASR APPLICATION

199