SEMANTIC MEDIA ANALYSIS FOR PARALLEL HIDING OF DATA

IN VIDEO AND AUDIO TRACK

Stanisław Badura and Sławomir Rymaszewski

Information Technology and Electronics Department, Warsaw University of Technology, Warsaw, Poland

Keywords:

Audio steganography, video steganography, DWT, data hidding, cash machine.

Abstract:

This paper is dealing with the role of steganography in system of intelligent cash machines. Hiding methods

dedicated especially for this application are presented. In the system typical content protection was extended

by hiding multistream secret additional information. Video ﬁles with concealed information are stored in

the system by monitoring subsystem (Controll AV recording and storage) and third part has no possibility

to delete, add or change video archives. Two different steganography methods were mixed to prepare more

advanced approach.

1 INTRODUCTION

Data hiding has a various applications in multimedia

area. In this paper are proposed data hiding methods

for a speciﬁc implementation. They are used as a part

of intelligent cash machine system. The base concept

is assuming that the cash machine is interactive, user-

friendly and safe. It is obvious that the last require-

ment is very important. There exist some methods

ensuring high security for cash machines and mes-

sage exchanging with central computer system. These

are usually cryptography and public key infrastructure

based methods. Our goal is to add extra security tools

based on data hiding which increase safety and facil-

itate investigation in case of protection violation.

The intelligent cash machine system includes a

surveillance module registering an interactive session

between user and cash machine and other events gen-

erated by accidental person or intruders. The regis-

tered audiovisual material is taken by cameras and

microphones at the cash machine. In next step an ad-

ditional information (metadata) is hidden into mate-

rial in such a way that the data can not be removed

without destroying host media. As metadata are used

time and date information, cash machine id, and per-

sonal data of a client. In case of destruction or re-

placement the original material with fabricate one, it

is impossible to retrieve hidden metadata, what de-

tects a violation case.

The following sections contain details of the algo-

rithm. Section 2 describes general data hiding con-

cept. Section 3 provides the methods to ensure data

robustness. In section 4,5 algorithms of audio and

video steganography are described in details. Last

two sections include experiments, their results, and

ﬁnal conclusions.

2 GENERAL DESCRIPTION OF

THE SYSTEM

In Fig.1 general idea of metadata hiding in multime-

dia stream is presented. Original data D is duplicate

three times (D1,D2,D3) and send to blocks which are

transfered to inputs of three different subsystems to

conceal data:

1. subsystem using only audio information as host

medium (Block 1),

2. subsystem using only video information as host

medium (Block 2),

3. subsystem hiding data from input in audio and

video stream (Blocks 1,2 and 3).

To ensure indexed data integrity, safety and robust-

ness for intentional attacks of metadata hidden in mul-

timedia material. Block 1 and Block 3 include spe-

cial subblocks which prepare data for hiding and have

special methods to increase robustness, which are de-

scribed in section 3.

In Block 2 the raw data D2 and secured data from

Block 3 output S(DV) is hidden in video content and

462

Badura S. and Rymaszewski S. (2007).

SEMANTIC MEDIA ANALYSIS FOR PARALLEL HIDING OF DATA IN VIDEO AND AUDIO TRACK.

In Proceedings of the Second International Conference on Signal Processing and Multimedia Applications, pages 452-458

DOI: 10.5220/0002141804520458

 SciTePress

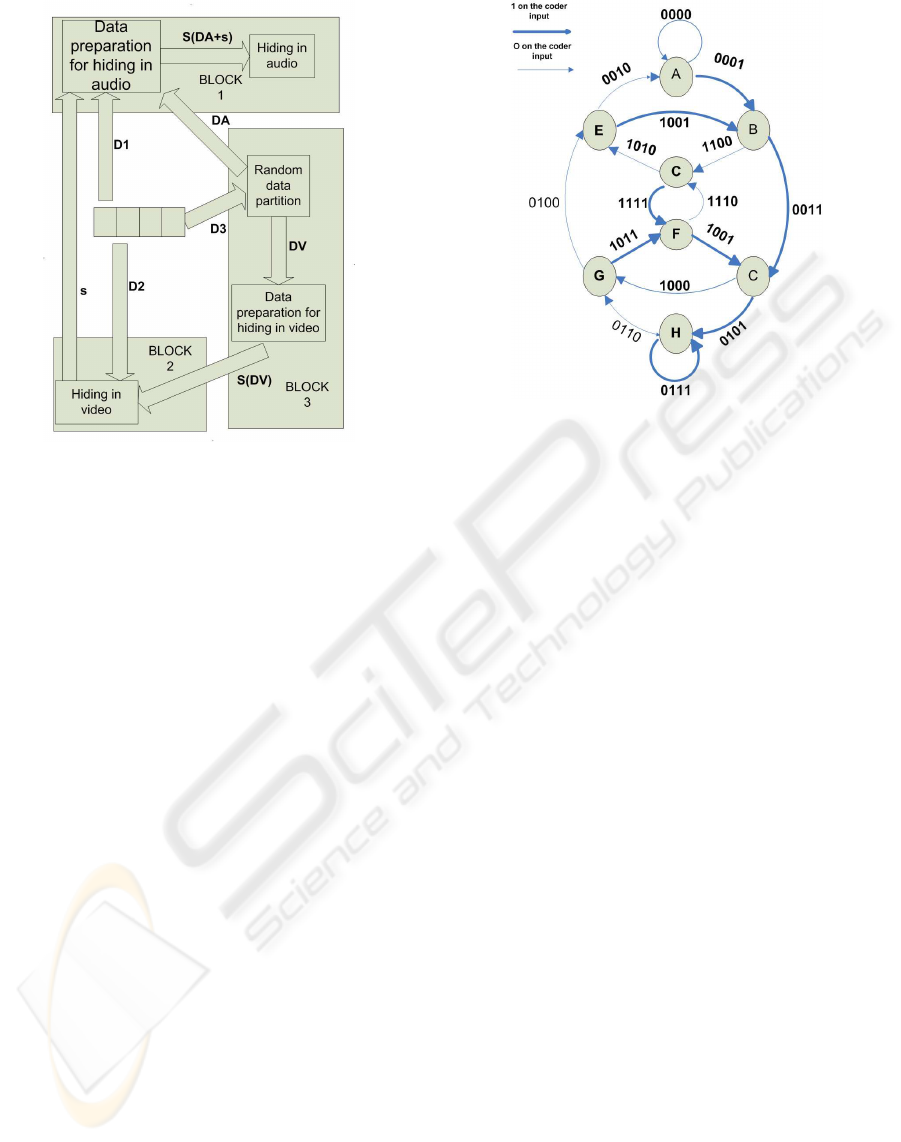
Figure 1: Method for parallel hiding of monitoring subsys-

tem information data in video and audio track.

MD5 function result (s) is generated using bits of

video after hiding process. Next data D1 and s are

secured and embedded in audio stream.

The fact that algorithm of data hading in video is

very fragile causes that intruder has no possibility to

attack the multimedia stream. Modiﬁcation will be

detected by:

1. ﬁnding the differences between data D1 with D2

or D3,

2. MD5 results with s comparison.

3 ADDITIONAL METHODS TO

PROVIDE DATA ROBUSTNESS

To ensure robustness we use two technics for the data

hidden in audio (D1) and for part of the data hidden

in video (DV):

1. pseudorandom permutation of bits with seed un-

know for third part persons,

2. pseudorandom partition of bits in block Random

Partition Block with seed unknow for third part

persons,

3. Viterbi’s error correction codes (Fig.2) ((Inge-

mar J.Cox, 2001)).

Figure 2: State graph of Viterbi coder used in the system.

4 AUDIO STEGANOGRAPHY

ALGORITHM

The main concept is based on DWT (Discrete Wavelet

Transform) and general idea is illustrated in Fig.3. An

audio record is divided into blocks of samples. For

each audio block H-level DWT is performed. In next

step the embedded position is selected.

In order to take the advantage of frequency mask-

ing effect of human auditory system and develop the

robustness against variety signal attacks such as nois-

ing, low pass ﬁltering, subsampling, requantization

and mainly against lossy compression. In the scheme

one bit of secret message is embedded into selected

DWT coefﬁcient. The embedding process is con-

trolled by a quantization step parameter. Finally to

form stegoaudio Inverse Discrete Wavelet Transform

is performed. This simple method has some disad-

vantages. Using the same embedded threshold for all

audio blocks causes an audibility distortion or low ro-

bustness against signal attacks. In addition it strongly

depends on characteristic of sound i.e. the kind of mu-

sic, singer, speaker etc. We used the extended method.

The quantization step is adaptively selected to char-

acteristic of a given sound block and its surroundings.

According to the requirements we have applied fuzzy

clustering algorithm. A local audio features have to be

calculated before the clustering analysis is performed.

The membership value of all clusters is used to choose

appropriate quantization step.

It was a short introduction to an idea of how to

improve the basic steganography algorithm based on

DWT. The scheme of hidden data extraction is pre-

SEMANTIC MEDIA ANALYSIS FOR PARALLEL HIDING OF DATA IN VIDEO AND AUDIO TRACK

463

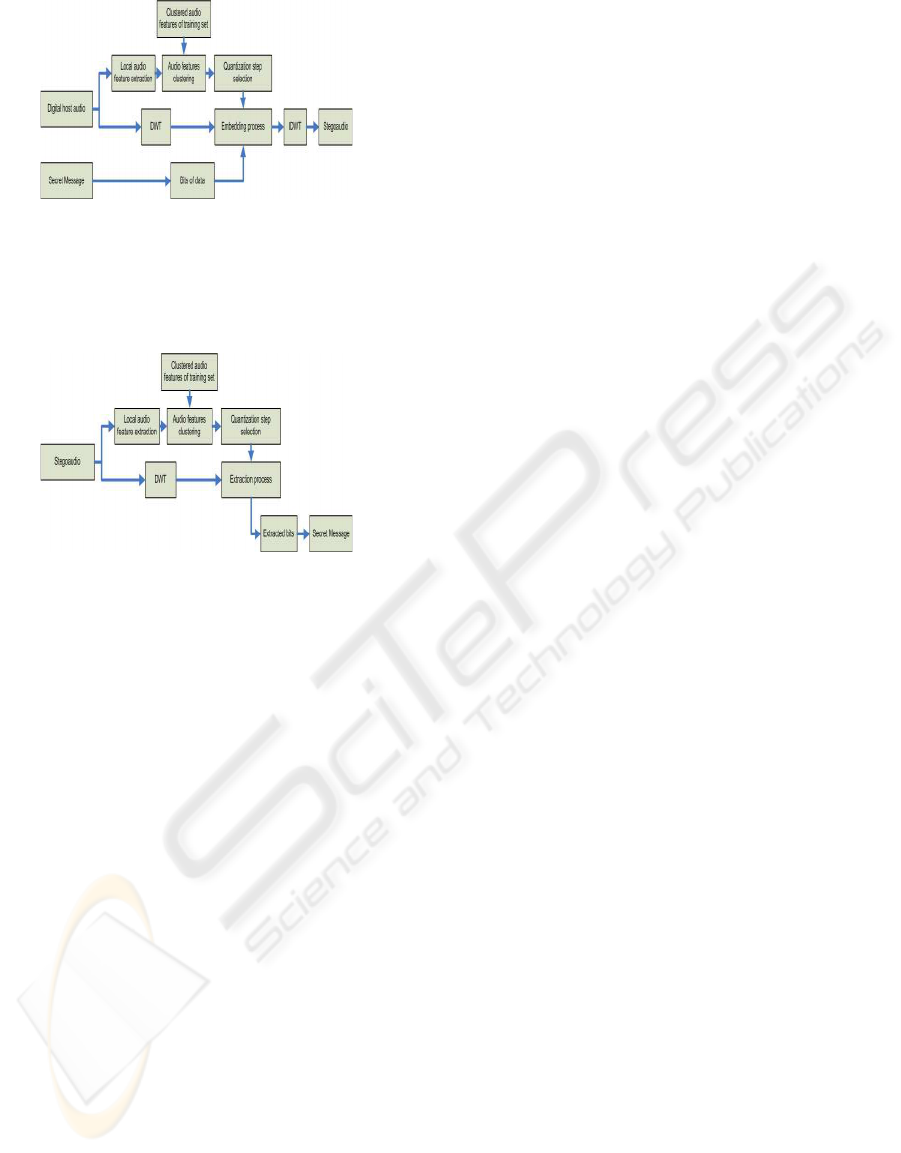
Figure 3: Data hiding in digital audio scheme.

sented in Fig.4. As we can see a whole extraction

algorithm is similar to above described hiding idea.

The following subsections contain details of the algo-

rithm.

Figure 4: Data extraction from stegoaudio scheme.

4.1 Adaptive Quantization Step

Selection

The quantization step has an important role in trans-

parency and robustness in the audio steganography al-

gorithm. The larger the quantization step is, the more

robust becomes hidden information against signal at-

tacks, but more perceptible the hidden information is.

However the smaller size of quantization step will in-

ﬂuence the robustness. If the same quantization step

is adopted for the whole host audio, probably it will

cause one or both of the problems in some parts of the

host audio. So the quantization should be selected ac-

cording to the local audio correlation, human auditory

masking and possible signal attack.

Digital audio itself always has various auditory

features. It is very important to choose these, which

represent different parameters of the digital audio and

allow to selected appropriate embedded threshold. A

single bit is hidden in a short audio block. So in this

case an audio features should be computed for audio

samples from given audio block or from its neigh-

boring if the block is very short. Too short block

might to cause distortion of the computed features

value. In addition the values should be independent

from length of the audio block for a given range. To

meet above requirements, based on reviews and expe-

rience reported in papers (Peeters, 2004; E.Schubert,

2004; S.H.Srinivasan, 2003; Wang Xiang-yang, 2004;

Changsheng Xu, 2002), we have selected audio fea-

tures such as fundamental frequency, short time

mean energy, harmonic concentration, spectral cen-

troid, harmonic energy distribution, max energy, zero-

crossing rate.

Values of the features for a single digital audio

block form a feature vector X

{

, x

, . . . , x

}

which determine a point in 9-dimensional space.

Such a vector is computed for each audio block from

all training audio records. All vectors construct a data

set X. Similarity between some vectors gives a way

to ﬁnd a common quantization step for close located

points. To group them we haveused the fuzzy C-mean

clustering (J. C. Bezdek, 1987) algorithm. As a result

we get the centers of groups. For each center we adopt

separate quantization step T

4.2 Fuzzy Clustering Algorithm

Let X be a data set, and x

denotes one sample

(i = 1, 2, . . . , N). The goal of clustering is to partition

X into K(2 ≤ K ≤ N) subsets or representatives clus-

ters, and make most similar samples be in the same

cluster if possible. The typical clustering algorithm

gain is to strictly classify each sample to a certain

cluster. However, as a matter of the fact, there is often

no explicit characteristic with which the sample can

be grouped. Many samples belong to several clus-

ters. Under that situation, the fuzzy clustering algo-

rithm could provide a better performance. The fuzzy

clustering algorithm divides data set X into K clusters

according to fuzzy membership u

(0 ≤ u

≤ 1) that

represents the degree by which the sample x

belongs

to k − th (k = 1, 2. . . , K) cluster. So the results of the

clustering can be described as a N × K matrix, that is

composed by each u

, and

∑

k=1

= 1; 0 <

∑

i=1

< N. (1)

Proposed by J.C.Bezdek (J. C. Bezdek, 1987), the

fuzzy C-mean clustering algorithm seeks to ﬁnd fuzzy

division by minimizing the following objective func-

tion:

(U,V) =

∑

k=1

∑

i=1

)

−V

), (2)

where:

N - the number of feature vectors,

K - the number of clusters (partitions),

q - weighting exponent (fuzziﬁer; q > 1),

- the i-th membership function on the k-th cluster,

- the center of k-th cluster,

- the i-th feature vector,

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

464

−V

) - distance between the feature vector X

and the center of cluster V

Larger membership values indicate higher conﬁdence

in the assignment of the feature vector to the cluster.

A process of fuzzy clustering can be described by fol-

lowing steps :

1. Choose primary cluster prototypes V

for the val-

ues of the memberships;

2. Compute the degree of membership for all feature

vectors in each cluster:

−V

)

∑

k=1

−V

)

, (3)

where :

p =

q−1

; (4)

3. Compute new cluster centers V

∑

i=1

[(u

)

]

∑

i=1

[(u

)

]

; (5)

4. Iterate back and forth between (2) and (3) until

the memberships for successive iteration differ by

more than some prescribed value of termination

criterion ε.

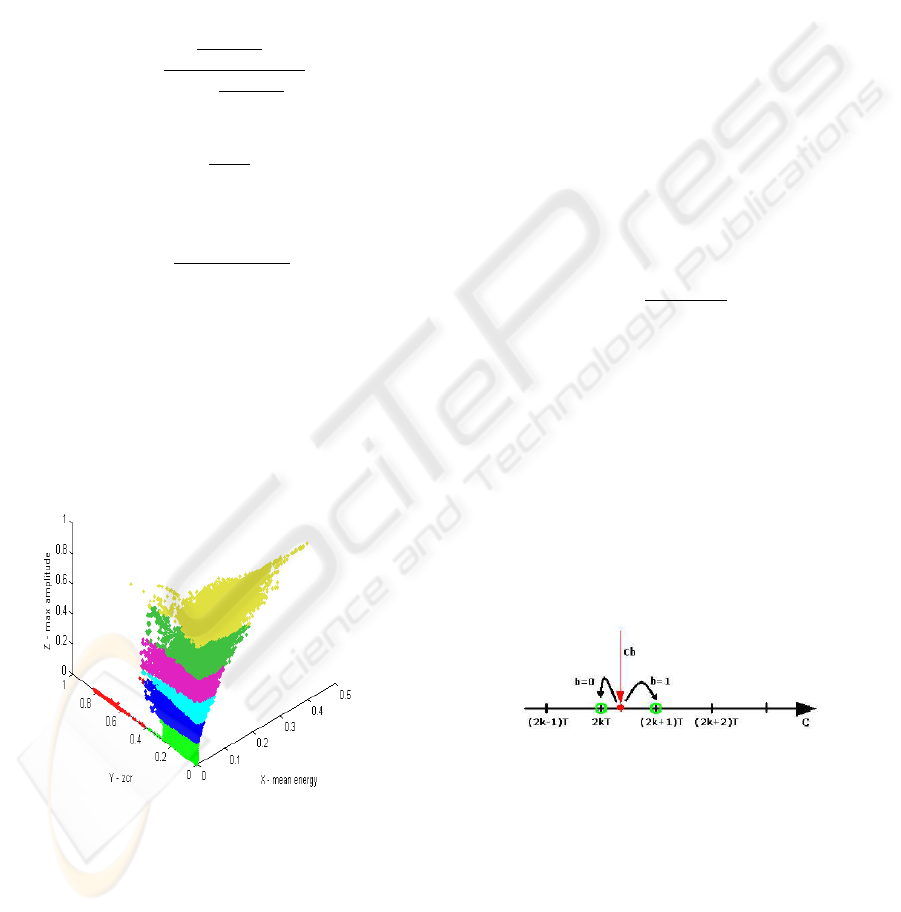
As an example and illustration of clustering results

of chosen three audio features sets is shown in Fig.5.

On the picture example each feature vector is strictly

partitioned to a certain cluster.

Figure 5: Example of clustering results.

4.3 DWT

For each audio segment A(i), H-level DWT is per-

formed [11], and we get the wavelet coefﬁcients

of C(i)

, D(i)

H−1

, . . . , D(i)

where C(i)

is the coarse signal and the detail signals are

D(i)

, D(i)

H−1

, . . . , D(i)

. The detailed coefﬁcients

correspond to the high frequency components and

the coarse coefﬁcients correspond to the low ones.

In order to balance the transparency and robustness,

the coefﬁcient d

(i)(1) from the detail components

D(i)H is selected for embedding a bit of information.

There are several advantages of applying DWT to data

hiding into digital audio:

• DWT has the time-frequency localization capabil-

ity,

• variable decomposition levels are available,

• DWT itself needs a lower computation load com-

pared with DCT and DFT.

4.4 Bit Embedding Scheme

In order to embed single bit in a single audio segment

a feature vector x

is computed. For the feature vector

a fuzzy membership u

is found. Finally, if we have

adopted quantization steps T

and the fuzzy member-

ship u

, we calculate adaptive quantization step T

∑

k=1

∑

k=1

. (6)

The embedding scheme is based on quantization pro-

cess and the idea is illustrated in Fig.6. The selected

DWT coefﬁcient C

= d

H(i)(1)

is quantized with a

given quantization step T, so the coefﬁcient value C

is rounded to multiple value of T. Depends on hidden

bit value b the coefﬁcient C

is rounded in different

way:

• if b = 1, the coefﬁcient C

is rounded to the near-

est odd multiple value of T,

• otherwise if b = 0, the coefﬁcientC

is rounded to

the nearest even multiple value of T.

Figure 6: Single bit embedding scheme.

After a bit of information is embedded, the modiﬁed

DWT coefﬁcient is placed back into structure of the

detail components D(i) H and H-level Inverse DWT

is performed. Retrieved audio segments form au-

diostream like host audio track.

SEMANTIC MEDIA ANALYSIS FOR PARALLEL HIDING OF DATA IN VIDEO AND AUDIO TRACK

465

5 VIDEO STEGANOGRAPHY

ALGORITHM

Many watermarking algorithms for video was

proposed (Adnan M. Alattar and Celik, 2003;

Yulin Wang, 2002; Hartung, 99; Changyong Xu,

2006). The majority of watermarking algorithms

operates directly in video compressed bit streams,

changing DCT coefﬁcients (Adnan M. Alattar and

Celik, 2003; Changyong Xu, 2006).

Method proposed by Wang (Yulin Wang, 2002)

used only I-frames for information hiding, other

methods (Changyong Xu, 2006; Adnan M. Alattar

and Celik, 2003) take also motion vectors in P-frames

and B-frames into consideration. Despite of these ex-

tensions for information hiding in video stream, high-

capacity steganography should use not only one type

of elementary stream.

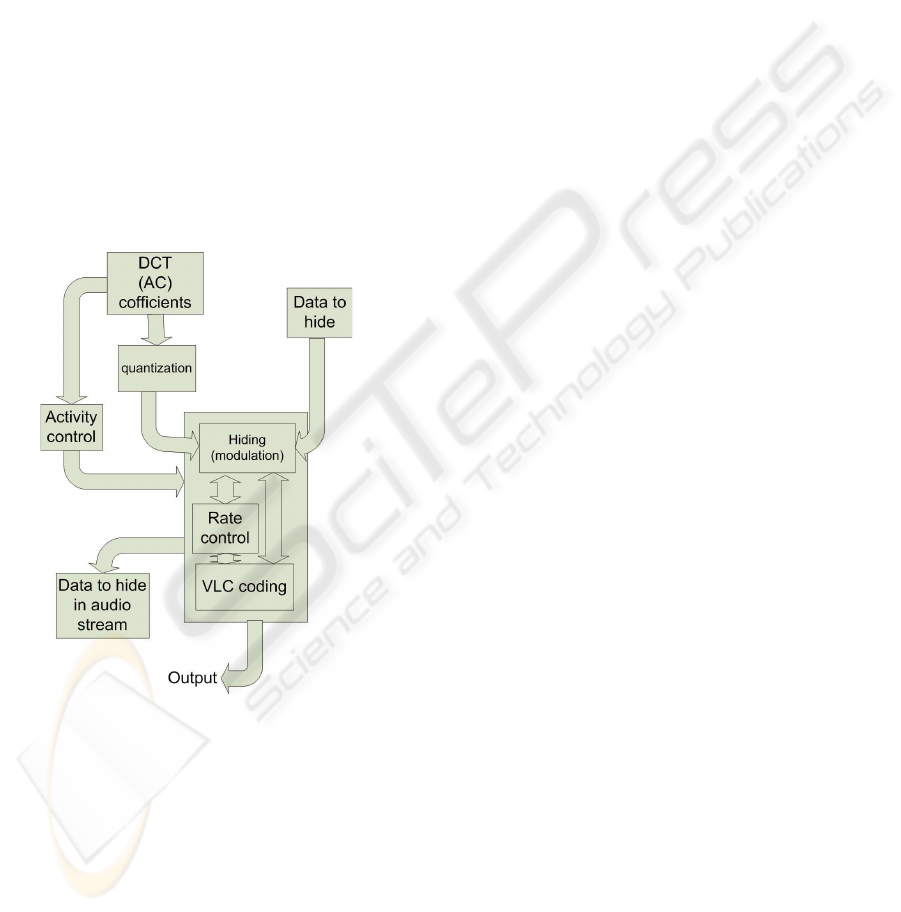
Block diagram (Fig.7) presents general idea of

hiding in video content.

Figure 7: Block diagram of the method of hiding data in

video stream.

Proposed video steganography method is based

on changing DCT coefﬁcients. In MPEG-2 stan-

dard the quantized DCT coefﬁcients are encoded us-

ing run/level encoding and subsequent variable length

coding (VLC) (ISO and IEC, 2000). Thus, sim-

ple DCT modulation could dramatically change the

amount of bits in video stream. This fact could cause

increase of probability that stegocommunication will

be noticed by third person. To prevent against this sit-

uation some methods were previously developed: we

can ﬁnd the quantized coefﬁcient with the same length

of bit representation or resign from hiding bit in this

coefﬁcient (Hartung, 99).

In our system we use different algorithm. In MPEG-2

Program Stream the bit rate is calculated using time

stamps, so we ensure constant bit rate on higher level

then single VLC-codes. The method does not change

the bitrate for each block of bits between timestamps

Fig. (8). This modiﬁcation gives higher capacity.

This task was gained by Algorithm 1.:

Algorithm 1.

1. Classiﬁcation of VLC ( run, level,length) coded

coefﬁcients in three sets:

(a) pairs of coefﬁcients sequence coded using

escape

method with constant length code (set

A),

(b) pairs of coefﬁcients sequence coded with the

same length of VLC code and run but with

difference between level values equals to 1 (set

B),

same run value but difference between level

values lower than 2, different lengths of VLC

code, but levels≥ T (for example (1,5,8) and

(1,6,13))(set C),

(d) codes useless for hiding (set D);

2. Hiding the bits by replacement the VLC code by

another code from pair:

(a) if level after change is odd, 0-bit was hidden,

(b) if level after change is even, 1-bit was hidden.

In step 2. pairs are chosen from sets A, B or C. One

VLC code can be in the pair in set B and C, only in

B or only in one set (A,C,D). Algorithm prefers more

VLC codes from pairs in set B than C. Set C is used

by Rate Control Block to provide the same bitrate of

MPEG video stream. Rate Control Block stops pro-

cess of data hiding if replacement of VLC codes from

C) set does not guarantee the same amount of bits be-

tween time stamps.

To ensure hidden information invisibility only

DCT AC coefﬁcients with value higher then thresh-

old are changed in each macroblock. The algorithm

is adaptive, because thresholds are determined after

observation of blocks activity. In proposed method

audio stegochannel contains information useful to re-

store hidden bits from video stream (information for

stego-decoder, how many last coefﬁcients before next

time stamp were skipped in hiding process by rate

control block (Fig.7).

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

466

Figure 8: MPEG 2 PES packets structure with time stamps.

6 EXPERIMENTS

6.1 Experiments for Audio

In order to illustrate the performance of presented

here steganography algorithm, robustness subjective

test were carried out.

6.1.1 Conditions for Audio Stagnography Tests

1. Training stage. A training procedure was con-

ducted to determine the centers of groups of au-

dio segments. Different group will use different

quantization step T

. In our method the fuzzy K-

mean clustering algorithm is used to group audio

segments into four groups. In order to make train-

ing results statistically signiﬁcant, training data

should be sufﬁcient and cover various genre of au-

dio. Two audio examples were selected: speech

track, tracks with music in the background. All

data were 44.1 kHz sample rate, one channel and

16 bits per sample. Each audio track was divided

into overlapping segments, and the length of each

segment was 1024 sample points.

2. Quality measure. The audibility is estimated by a

simple subjective listening test. A listener com-

pares the representation of the reference audio

track with that of the audio track under test. Fi-

nally the listener afﬁrms if audio quality is de-

graded, which is equivalent to audibility of hid-

den image in the audio track. Only inaudible

cases are further taken under robustness test. As

a robustness test we used the Normalized Cross-

correlation (NCC) which is adopted to appraise

the similarity between the extracted binary image

and the original one:

NCC =

∑

m,n

∑

m,n

, (7)

where:

m,n

- original bit at position (m,n),

m,n

- extracted bit at position (m,n).

3. Robustness test. We evaluated the robustness of

data hiding in speech recording to audio com-

pression, requantization, subsampling and addi-

tive noise. In the test, a 64x64 bit binary image

was hidden in a audio track (one channel, 16 bits

per sample and 44.1 kHz sample rates). The au-

dio track is divided into 128 samples length seg-

ments, but the audio feature vector is computed

for longer block (1024 samples length) including

the segment in the middle position and its adjacent

audio samples. The Daubechies-1 wavelet basis is

used, and 7-level DWT is performed.

The data was hidden without protection codes to show

robustness of audio algorithm in visible way. Error

correction code increases NCC up to near 100 %.

6.1.2 Audio Steganography Results

The results of tests are presented in Table 1 and 2 for

an audio track with speech and track with pop music

in the background:

Table 1: Results for data hiding in speech track.

6.2 Experiments for Video

The used video material (Fig. 9) was stored with typ-

ical for SD quality and resolution. The video stream

capacity for each I-frame could be estimated as 3-4

KB, with PSNR=43 dB. Some techniques change not

only VLC DCT AC coefﬁcients but moving vectors

too, what gives the possibility to hide information in

P-frames and B-frames. In normal use this solu-

tion increases stegocapacity, but when static scenery

SEMANTIC MEDIA ANALYSIS FOR PARALLEL HIDING OF DATA IN VIDEO AND AUDIO TRACK

467

Table 2: Results for data hiding track with pop music in the

background (Norah Jones).

(typical for registered by camera built in typical cash

machine) is monitored, small amount of motion vec-

tors, with relatively big length are produced in coded

video. Modulation of short vectors give low capac-

ity, low PSNR values and higher complexity of stego-

codec, as the result of this observation, we decide to

use only Intra-blocks.

Figure 9: I-frame of video content used for tests.

7 CONCLUSION

Proposed method of steganography in more than one

stream is advanced and effective approach, which in-

creases system security. Using fragile and robust

technics of hiding in one system is interesting exten-

sion. Increase of capacity of host streams is not so

important in point of view hiding small amounts of

bits in intelligent cash machine system but gives pos-

sibility to use effective error correcting codes.

The initial research and obtained promising re-

sults, conﬁrm that established assumption are right.

Further work on data hiding allows to design the high

quality tools for improving security of the intelligent

cash machine.

ACKNOWLEDGEMENTS

The work presented was developed within VIS-

NET 2, a European Network of Excellence

(http://www.visnet-noe.org), funded under the

European Commission IST FP6 Programme.

REFERENCES

Adnan M. Alattar, E. T. L. and Celik, M. U. (2003). Digital

watermarking of low bit-rate advanced simple proﬁle

mpeg-4 compressed video. In IEEE Transactions on

circuits and system for video technology, Vol. 13, No.

8, August 2003 787.

Changsheng Xu, D. D. F. (2002). Robust and efﬁcient

content-based digital audio watermarking. In Multi-

media Systems, Vol8, p. 353-368,. Springer-Verlag.

Changyong Xu, Xijian Ping, T. Z. (2006). Steganography

in compressed video stream. In Proceedings of the

First International Conference on Innovative Comput-

ing, Information and Control,Information and Control

(ICICIC ’06).

E.Schubert, J.Wolfe, A. (2004). Spectral centroid and tim-

bre in complex, multiple instrumental textures. In Pro-

ceedings of the 8th International Conference on Music

Per-ception and Cognition. Evanston Illinois, USA.

Hartung, F.; Kutter, M. (99). Multimedia watermarking

techniques. In Proceedings of the IEEE Volume 87,

Issue 7, July 1999 Page(s):1079 - 1107.

Ingemar J.Cox, Metthew L.Miller, J. A. (2001). Digital

Watermarking. Springer-Verlag, ISBN: 978-1-55860-

714-9, 1st edition.

ISO and IEC (2000). Iso and 13818-2:2000 standard. In

Generic coding of moving pictures and associated au-

dio information: Video.

J. C. Bezdek, e. (1987). Convergence theory for fuzzy c-

means: Counterexamples and repairs. In IEEE Trans.

Syst., September/October. IEEE Press.

Peeters, G. (2004). A large set of audio features for sound

de-scription in the cuidado project. In IEEE Trans.

Syst., September/October. Icram, Paris, France,.

S.H.Srinivasan, M. (2003). Harmonicity and dynamics

based audio separation. In ICASSP.

Wang Xiang-yang, Y. H.-y. (2004). A new content-based

digital audio watermarking algorithm for copyright

protection. In Proceedings of 2004 International Con-

ference on Information Security Shanghai,China, p

62-69, ISBN:1-58113-995-1. ACM Press.

Yulin Wang, Izyguierdo Ebroul, L. P. (2002). High-capacity

data hiding in mpeg-2 compressed video. In IWS-

SIP’02 No9, Manchester, ROYAUME-UNI 2002, pp.

212-218.

SIGMAP 2007 - International Conference on Signal Processing and Multimedia Applications

468