
TRANSMISSION POWER CONTROL FOR AVOIDING CELL
OVERLAPPING IN MICRO-CELLULAR NETWORKS
Akiko Miyagawa
Graduate School of Information Science and Technology, Osaka University, 1-5 Yamadaoka, Suita, Osaka, Japan
Masahiro Sasabe, Hirotaka Nakano
Cybermedia Center, Osaka University, 1-32 Machikaneyama, Toyonaka, Osaka, Japan
Keywords:
Complete cell partitioning, transmission power control, mobile communication, high-speed data transfer, in-
formation distribution, radio interference.
Abstract:
In a cellular system, a base station can smoothly communicate with nodes in its cell by avoiding overlap
of frequency range with its adjacent cells. From the viewpoint of graph theory, that needs to divide the
original frequency range into at least four sub-ranges. This leads to deteriorate the transmission rate. To tackle
this problem, we propose Complete Cell Partitioning (CCP) that enables a base station to use the whole of
the original frequency range by avoiding overlap of its own cell with the adjacent cells. CCP is achieved
by appropriately controlling the transmission power on base stations. We first analytically derive success
probability of CCP when nodes are randomly located in the whole region. Then, we verify the analysis by
comparing with simulation results. The analytical and simulation results show that CCP enables to use the
original frequency range more effectively than the traditional cellular system regardless of the number of
nodes in a cell.
1 INTRODUCTION
Mobile communication technologies (Schiller, 2000;
Siau and Shen, 2003) which play important roles in
ubiquitous networks have attracted extensive research
efforts in recent years. In the traditional mobile com-
munication services, voice and mail data occupied the
large portion of traffic. Such data can be transmitted
at a relatively low bit rate. In recent years, cellular
phone service providers offer a flat-rate plan (Marcus,
2004) independently of the amount of consumed traf-
fic. This new type of service plan enhances users to
download short movies and music. In addition, a shop
may want to distribute advertising information to peo-
ple when they get close to it. In both types of service,
network capacity and transmission rate become more
important.
A cellular system (Lee, 1995; Castafieda-
Camacho and Lara-Rodriguez, 2000) is an infrastruc-
ture used in a mobile communication between a cel-
lular phone, called a node, and a base station. In the
system, a service region is divided into multiple sub-
regions, called cells. In every cell, a base station is
located at the center and communicates with a node
using a wireless connection. In the traditional cellular
system, the size of a cell is as large as several kilome-
ters. Such a large cell is called a macro-cell (I et al.,
1993). A system administrator designs the size of a
macro-cell so that the service area is fully covered by
the macro-cells while allowing adjacent cells to over-
lap each other (Chen, 1994; Camp et al., 2000). This
structure is effective for calling because a node can
communicate wherever it is located in the service re-
gion.
However, to avoid the radio interference, a base
station must use the radio wave whose frequency
range is different from those of the adjacent base sta-
tions. From the viewpoint of graph theory, this needs
to divide the original frequency range into at least four
sub-ranges (Robertson et al., 1997). This leads the
degradation of transmission rate. We expect that the
transmission rate becomes more important in the in-
formation distributing service e.g., advertisement ser-
vice with which a shop provides people who get close
to it. If a system administrator does not need to di-
vide the original frequency range, the transmission
rate does not deteriorate. Appropriately controlling
the transmission power leads the avoidance of cell
overlapping and enables to use the whole of original
frequency range. As a result, it achieves about four
45
Miyagawa A., Sasabe M. and Nakano H. (2007).
TRANSMISSION POWER CONTROL FOR AVOIDING CELL OVERLAPPING IN MICRO-CELLULAR NETWORKS.
In Proceedings of the Second International Conference on Wireless Information Networks and Systems, pages 45-50
DOI: 10.5220/0002145700450050
Copyright
c
SciTePress

times higher transmission rate than the traditional cel-
lular system. We call this scheme as “complete cell
partitioning (CCP).”
In this paper, we propose CCP for information dis-
tributing service of a shop. A shop may want to dis-
tribute advertising information to people when they
get close to it. On the occasion, it should not dis-
turb the communication of its adjacent shops. Thus,
it had better prevent radio interference among them. If
a base station can achieve high-speed data transfer, it
can distribute a large volume of multimedia contents
that seems to be more attractive for people than text-
based contents. In this case, CCP is accomplished
when a base station can adjust the size of the cell so
that a node belonging to an adjacent cell does not exist
in the vicinity of border among adjacent cells.
We expect that CCP tends to succeed when the
cell size becomes small. This is because nodes in
the vicinity of the border among cells decrease in
response to the reduction of the cell size. In re-
cent years, various wireless technologies which have
micro-cells (Lee, 1995), such as Bluetooth (Haart-
sen and Ericsson Radio Systems B.V., 2000) and Zig-
Bee (Zigbee Alliance, 2007), have been widely de-
ployed. Thus, CCP is expected to be one of key con-
cepts achieved over these technologies.
We first propose CCP that is based on a radio in-
terference model. Then, by using analytical approach,
we derive the success probability of CCP, the proba-
bility that a node can communicate with a base sta-
tion, under the following assumptions.
• The region is divided into multiple cells each of
which shapes a regular hexagon.
• Nodes are located at random positions in the re-
gion.
• CCP is applied to download link, while upload
link uses the traditional cellular system. In mo-
bile communications, the size of download data is
much larger than that of upload data. Therefore,
download link requires much transmission rate.
Through simulation experiments, we verify the anal-
ysis and show the effectiveness of CCP.
The remainder of this paper is organized as fol-
lows. In Section 2, we introduce the radio interference
model to explain CCP. In Section 3, we formulate the
condition of CCP and analyze the success probability.
Finally, Section 4 gives conclusions of this paper.
2 RADIO INTERFERENCE
MODEL
We first introduce a model of radio interference in
wireless networks. In general, a radio wave is at-
tenuated in inverse proportion to α-th power of dis-
tance (Grossglauser and David N. C. Tse, 2002;
Gupta and Kumar, 2000). Suppose that a base sta-
tion bs emits a radio wave with transmission power P.
Then, power P(i) that a node X
i
receives from bs is
expressed as
P(i) =
P
|X
i
−bs|
α
. (1)
As shown in Fig. 1, perceived radio quality at X
i
is
differentiated by the distance from bs.
• If |X
i
−bs| ≤ r
c
, X
i
is in a success zone where it
can receive data from bs correctly.
• If r < |X
i
−bs| ≤ ∆r
c
, X
i
in a noise zone where it
receives data from bs as noise.
• If ∆r
c
< |X
i
−bs|, X
i
is in no interference zone
where it does not receive data from bs.
Here, we call ∆ as occupation ratio that determines
the area occupied by bs. The radius of a success zone
r
c
is controlled by adjusting the transmission power.
3 COMPLETE CELL
PARTITIONING
3.1 Formulation of Condition for CCP
In this section, we formulate the condition of CCP for
information distribution service. In this case, a base
station is responsible for the connections to available
nodes in its maximum transmission range. We denote
the nodes as X
i
in an ascending order of the distance
from the base station bs. X
i
(1 ≤ i ≤ n) is in its maxi-
mum transmission range while X
i
(n+ 1 ≤ i) is out of
the range. bs first finds maximum i that satisfies the
following condition:
|X
n+1
−bs| ≥ ∆|X
i
−bs|
and |X
n+1
−bs| < ∆|X
i+1
−bs|,
(2)
then adjusts the radius of success zone as |X
i
−bs|.
Note that X
n+1
is the nearest node out of the maxi-
mum transmission range of bs. Equation (2) indicates
that bs can connect to nodes in its success zone only
when there aren’t any nodes belonging to other base
r
success zone
noise zone
bs
Δr
no interference zone
Figure 1: Relation between radio attenuation and occupa-
tion ratio.
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
46

a unit
Figure 2: Sample distribution of nodes and base stations
when N
r
= 4.
stations in its noise zone. In CCP, bs generates the
radio wave at the cost of nodes which is belonging to
bs and in the noise zone. When each base station con-
trols its transmission power by such a method, avoid-
ance of radio interference leads CCP.
To realize this mechanism, each base station has
to collect information on nodes in its maximum trans-
mission range. In addition, it also needs to know ev-
ery other node belonging to its neighboring base sta-
tions. This information can be obtained by exchang-
ing node lists among neighboring base stations. The
detail of the mechanism is a future work.
3.2 Analysis
In this section, we analyze the success probability of
CCP. In the traditional analysis of a cellular system,
the area is assumed to be a repeat structure of one cell.
In this paper, we improve the precision of the analysis
by making a unit of the repeat structure larger. In what
follows, we explain the analysis in detail.
First, suppose that N
r
adjacent cells are periodi-
cally located in the region. If N
r
increases, we expect
accuracy of the analysis grows up. Figure 2 displays
a sample distribution of nodes and base stations when
N
r
= 4. A circle with dashed line and that with solid
line express a region and a cell, respectively. Each
cell that consists of the unit of the repeat structure is
surrounded with a thick line. A triangle and a dot rep-
resent a base station and a node, respectively.
As mentioned in section 1, we assume a cell is
shaped as a regular hexagon. Suppose that the length
of each edge of the hexagon is R. The radius R
eq
of
the equivalent circle whose area is equal to that of the
hexagon becomes
q
3
√
3
2π
R. Note that we do not lose
generality even if we set R
eq
to 1. In the following
analysis, we set R
eq
to 1. Moreover, suppose that node
density in a cell is n and the occupation ratio is ∆. We
also define the success probability of CCP P
success
(n)
as the probability that a node can communicate with
a base station.
In what follows, we analytically derive P
success
(n)
when N
r
= 1, 4.
3.2.1 In the Case of N
r
= 1
When N
r
= 1, only one type of cell is lined with the
region. We focus on the neighboring seven cells in the
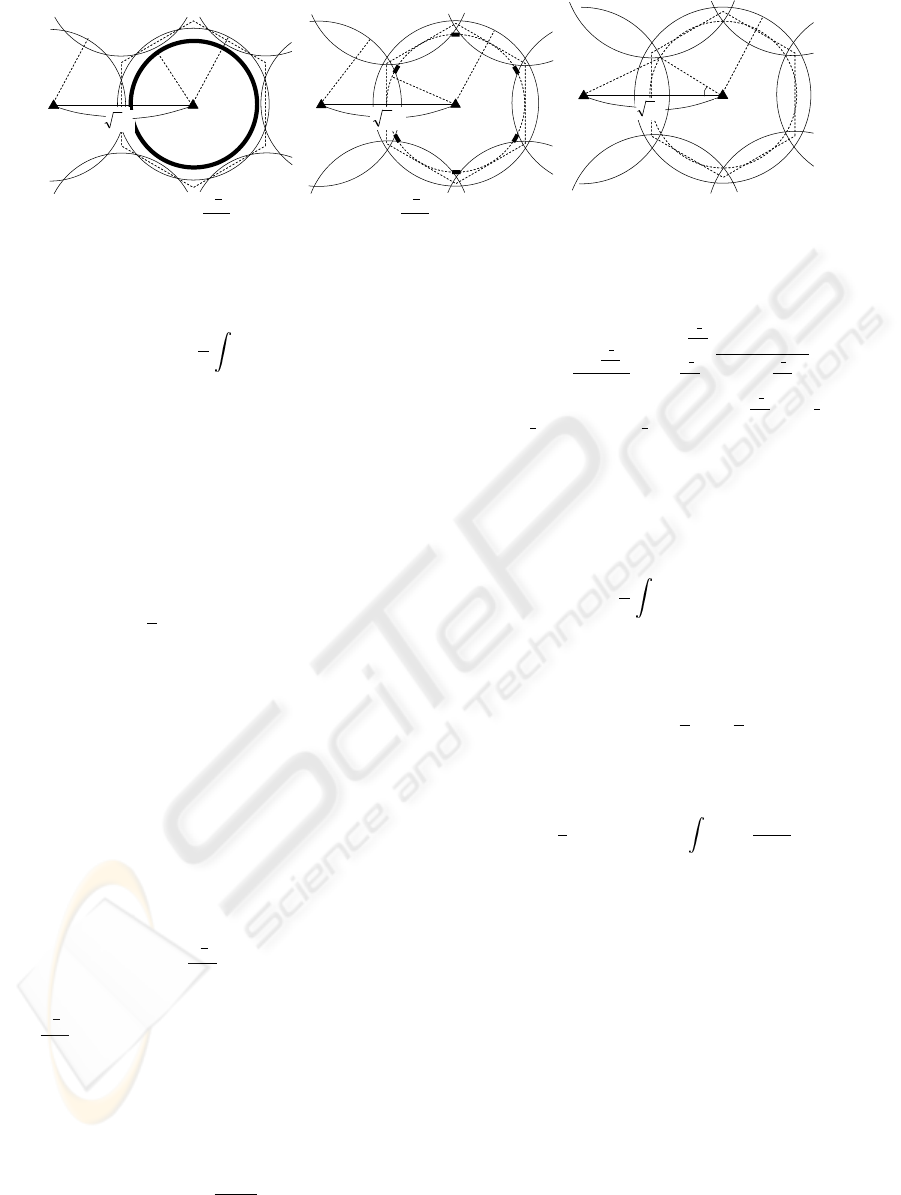
region, as illustrated in Fig. 3. A hexagon and a cir-
cle with solid line in these figures express a cell and
a range of max transmission power of a base station,
respectively. Define the center cell in the seven adja-
cent cells as a main cell and the others as neighboring
cells. In what follows, we focus on the main cell.
Suppose a base station in one of the seven cells
emits the radio wave so that a node whose distance
from the base station is less than r can communicate
with it. This distance in every cell equals to r since
the position of a node is invariant among cells when
N
r
= 1. For successful communication, nodes in the
main cell cannot exist in the noise zone of the adjacent
cells. As a result, the node located at a distance of r
from the base station bs in the main cell can exists
on the thick lines in Fig. 3. When r + ∆r ≤
√
3R,
the thick line equals to the circle whose radius is r
as in Fig. 3(a) because the success zone of the main
cell does not intersect the noise zones of the adjacent
cells. When
√
3R ≤ r + ∆r, the thick line becomes
as in Fig. 3(b). Moreover, the thick line disappeared
when r exceeds r
0
. r
0
is derived from the following
equation.
√
3R−
√
3
2
r
0
!
2
+
r
0
2
2
= (∆r
0
)
2
. (3)
Therefore, we get
r
0
=
√
3R
√
4∆
2
−1−3R
2(∆
2
−1)
. (4)
Thus, the most distant node which can communicate
with bs can exist in the area expressed as
S
1
=
1
0
S
b
(r)dr, (5)
where S
b
(r) is the sum of the length of the thick lines
and it is derived as
S
b
(r) =
2πr,
0 ≤r ≤
√
3R
∆+1
12r
n
π
6
−acos
n
3R
2
−(∆
2
−1)r
2
2
√
3Rr
oo
,
√
3R
∆+1
≤ r ≤ r
0
0, (r
0
≤ r ≤ 1)
The success probability equals to the ratio of nodes
in the area to all nodes in the main cell as follows:
P
success
(n) =
S
1
πR
2
eq
. (6)
According to R
eq
= 1, P
success
is derived as fol-
TRANSMISSION POWER CONTROL FOR AVOIDING CELL OVERLAPPING IN MICRO-CELLULAR NETWORKS
47
R3
r∆
r
r∆
bs
(a) 0 ≤ r ≤
√
3R
∆+1
R3
r∆
r
r∆
bs
(b)
√
3R
∆+1
≤ r ≤ r
0
R3
r∆
r
r∆
bs
(c) r
0
≤ r ≤ 1
Figure 3: The area the most distant node from bs can exist when N
r
= 1.
lows:
P
success
(n) =
1
π
1
0
S
b
(r)dr. (7)
3.2.2 In the Case of N
r
= 4
We analyze the success probability in the case of N
r
=
4. Define one cell from the four adjacent cells as a
main cell and the others as neighboring cells. In what
follows, we focus on the main cell. Suppose that there
are k ≤ 4n nodes in the main cell. In the case, the
success probability of CCP is defined as follows:
P
success
(n) =
1
n
4n
∑
k=1
{
k C
4
(n, k) P
s
(n, k)
}
, (8)
whereC
4
(n, k) is the probability that k nodes are in the
main cell and P
s
(n, k) is the mean success probability
in the main cell.
First, we derive P
s
(n, k) to obtain P
success
(n). Fig-
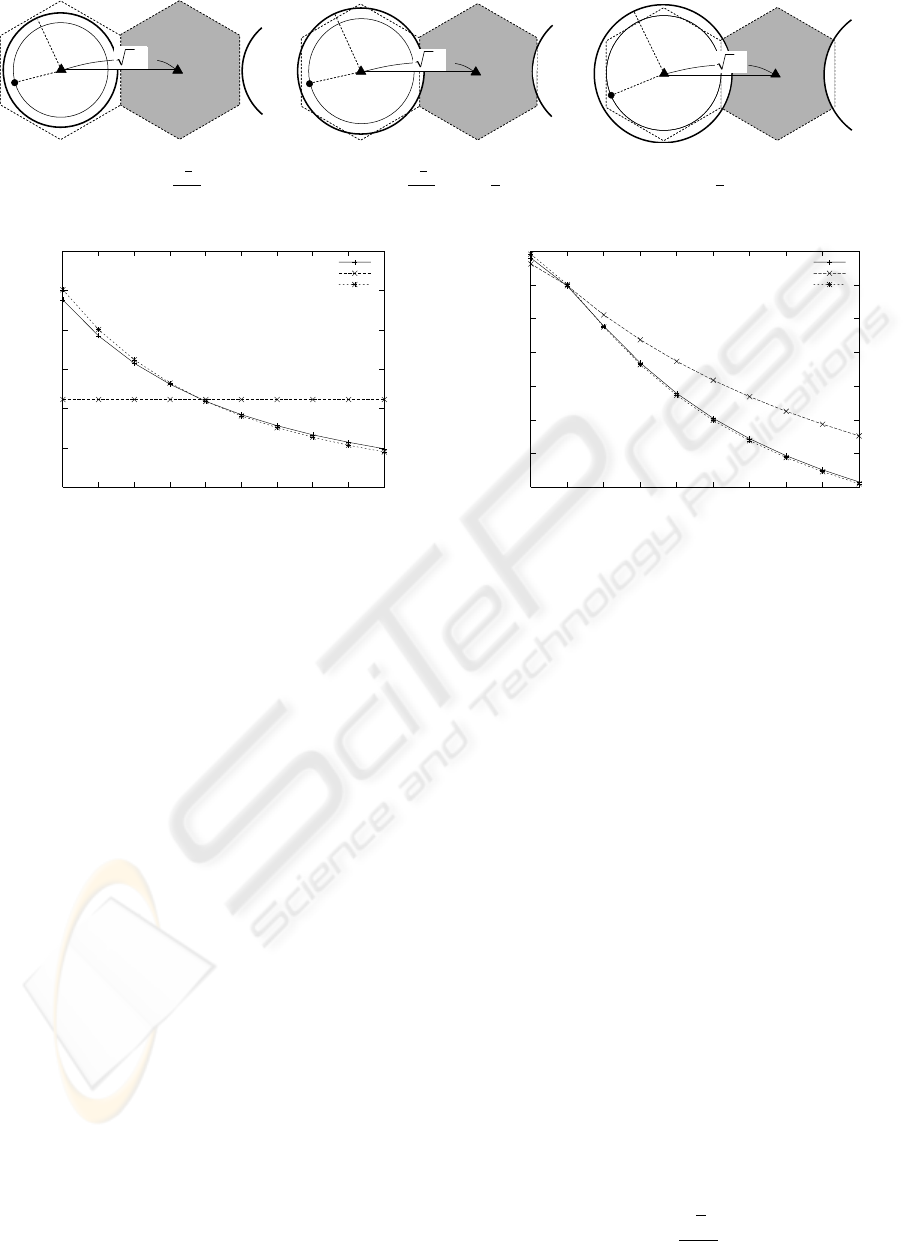
ure 4 illustrates the main cell, Cell
1
, and one of the
neighboring cells, Cell
2
, when the radius of the suc-
cess zone in Cell
1
is r. Cell
3
is the neighboring cell
of Cell
2
that faces Cell
1
. When N
r
= 4, node posi-
tions in Cell
1
and that in Cell
3
are same. Thus, in
Cell
3
, the radius of the success zone is r, too. In
this case, for successful communication in Cell
1
, the
nodes in Cell
2
cannot exist in the noise zone of Cell
1
and Cell
3
. Therefore, they must exist in the grey zone
in Fig. 4. When ∆r ≤
√
3R
2
, the circle with radius
∆r does not invade Cell
2
. Hence the nodes in Cell
2
can exist anywhere in Cell
2
as illustrated in Fig. 4(a).
When
√
3R
2
≤∆r, the grey zone becomes like Fig. 4(b)
and Fig. 4(c). The nodes in the other neighboring cells
must also exist in the grey zones of their belonging
cells. As a result, the probability that 4n −k nodes
in the three neighboring cells exists in the grey zones
becomes
p
ad j
(r, n, k) =
S
4
(r)
πR
2
eq
!
4n−k
, (9)
where S
4
(r) is the area of the grey zone and it is de-
fined as follows.
S
4
(r) =
π, (0 ≤r ≤
√
3R
2∆
)
π−4
acos
√
3R
2∆r
2
(∆r)
2
−
√
3R
4
r
(∆r)
2
−
√
3R
2
2
,
(
√
3R
2∆
≤ r ≤
R
∆
)
π
3
4−(∆r)
2
, (
R
∆
≤ r ≤ 1)
p
ad j
(r, n, k) means the success probability when the
radius of the success zone in Cell
1
is r. This equals
to probability that a node whose distance from bs
1
is
r succeeds in communication. Since P
s
(n, k) is the
mean success probability in Cell
1
, P
s
(n, k) becomes
as
P
s
(n, k) =
1
π
1
0
2πrp
ad j
(r, n, k)dr. (10)
Second, let’s derive C
4
(n, k). Because the node
density is n, the probability that the main cell includes
k nodes is defined as
C
4
(n, k) =
4n
C
k
1
4
k
3
4
4n−k
. (11)
By substituting Eq. (11) to Eq. (8), the success
probability becomes
P
success
(n) =
1
n
4n
∑
k=1
(
k C
4
(n, k)
1
0
2r
S
4
(r)
π
4n−k
dr
)
.
(12)
3.3 Simulation and Analytical Results
In this section, we verify the accuracy of our analy-
sis and show the effectiveness of our proposal. In the
following simulations, we set the number of base sta-
tions in the region to 250. We vary the number of
nodes in the region from 250 to 2500. Thus, the av-
erage number of nodes in a cell, that is node density
n, ranges from 1 to 10. Moreover, we suppose that
nodes are located at random positions in the whole
region. We define the success probability as the ratio
of the number of nodes that success in communica-
tion to the whole number of nodes. Note that we ig-
nore nodes near the border of the region because they
cannot belong to any base stations regardless of the
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
48
r∆
r
1
Cell
2
Cell
3
Cell
R3
2
bs
1
bs
(a) 0 ≤ r ≤
√
3R
2∆
r∆
r
1
Cell
2
Cell
3
Cell
R3
2
bs
1
bs
(b)
√
3R
2∆
≤ r ≤
R
∆
r∆
r
1
Cell
2
Cell
3
Cell
R3
2
bs
1
bs
(c)
R
∆
≤ r ≤ 1
Figure 4: The area the most distant node from bs can exist when N
r
= 4.
0.7
0.75
0.8
0.85
0.9
0.95
1
1 2 3 4 5 6 7 8 9 10
Psuccess
n
Simulation
Analysis(Nr=1)
Analysis(Nr=4)
(a) In the case of ∆ = 1.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
Psuccess
∆
Simulation
Analysis(Nr=1)
Analysis(Nr=4)
(b) In the case of n = 7
Figure 5: Accuracy of analysis.
transmission power control. In the following results,
we show the average of 1000 simulations.
3.3.1 Accuracy of Analysis
We verify the accuracy of our analysis by comparing
simulation results. Figure 5 shows the transition of
P
success
when ∆ = 1.2 and n = 7. The analytical results
in the case of N
r
= 4 are very close to the simulation
results compared to those in the case of N
r
= 1. As in
Fig. 5(a), the average difference is only 0.5 % when
N
r
= 4 and ∆ = 1.2 . Figure 5(b) also depicts that the
average difference is at most 1.1 % when N
r
= 4 and
n = 7. Thus it is clear that increase of N
r
contributes
to reduction of difference between analytical and sim-
ulation results.
Furthermore, those figures show that N
r
can be rel-
atively small to improve the accuracy of the analysis.
We use the analysis of N
r
= 4 as P
success
in the follow-
ing explanation.
3.3.2 Impact of Node Density and Occupation
Ratio
We investigate the feasible area of CCP through an-
alytical results. Figure 6 depicts the transition of
P
success
for CCP with the node density n and the oc-
cupation ratio ∆. P
success
falls down with the increase
of both of n and ∆. Now we examine the feasible
area that our proposal is more efficient than the tradi-
tional cellular system. We define radio utilization as
the product of available frequency range and the suc-
cess probability. As mentioned before, our proposal
can use about four times larger frequency range than
the traditional cellular system. Thus, in terms of the
radio utilization, our proposal is more effective than
the traditional cellular system when P
success
is larger
than 0.25. According to Fig. 6, CCP is more effective
than the traditional cellular system since the radio uti-
lization of CCP is constantly larger than 0.25 for ev-
ery n and ∆. Especially when ∆ is small, CCP can ac-
complish about 3-4 times higher radio utilization than
the traditional cellular system while suppressing the
sacrificed nodes.
3.3.3 Impact of Controlling the Transmission
Power
In this section, we examine the effect of controlling
the transmission power. First, we define the fixed
transmission power to satisfy the condition of CCP.
Suppose a base station emits the radio wave so that
the radius of its success zone equals to r
fix
. Since the
radio wave cannot disturb the communication in its
adjacent cells,
r
fix
=
√
3R
2∆
. (13)
TRANSMISSION POWER CONTROL FOR AVOIDING CELL OVERLAPPING IN MICRO-CELLULAR NETWORKS
49

1.9
1.8
1.7
1.6
1.5
1.4
1.3
1.2
1.1
1
10
9
8
7
6
5
4
3
2
1
0
0.2
0.4
0.6
0.8
1
Psuccess
CCP
Traditional cellular system
Fixed transmission power
∆
n
Psuccess
Figure 6: The success probability of CCP.
We define the scheme that every base station sets the
radius of its success zone to r
fix
as the fixed transmis-
sion power scheme. Then the success probability of
this scheme becomes as follows:
P
success
=
πr
2
fix
πR
2
eq
= r
2
fix
. (14)
Figure 6 also shows P
success
of CCP and that of
the fixed transmission power scheme. CCP is more
effective than the fixed transmission power scheme.
When ∆ = 1.2, for example, the differences between
P
success
of our proposal and that of the fixed transmis-
sion power scheme are up to 0.32.
4 CONCLUSION
In this paper, we proposed complete cell partition-
ing (CCP), a new scheme for transmission power con-
trol on base stations to avoid radio interference among
adjacent base stations. CCP enabled a base station to
use the whole of the original frequency range while a
base station could use a quarter of it in the traditional
cellular system. Then, we analyzed the success prob-
ability of CCP and verified the validity of the analysis.
Several simulation and analytical results showed that
the analysis was fully valid. Moreover, the results also
showed that CCP was more effective than the tradi-
tional cellular system from the viewpoint of the radio
utilization. For example, when the occupation ratio
was 1.2, CCP accomplished about 3-4 times higher
radio utilization than the traditional cellular system
while suppressing the sacrificed nodes.
As future works, we have to consider implemen-
tation of CCP on a real system. For example, a base
station needs to know the node positions in its maxi-
mum transmission range. We expect that Ultra Wide
Band (UWB) realizes it because UWB can measure a
position more accurately than GPS.
REFERENCES
Camp, T., Lusth, J., Matocha, J., and Perkins, C. (2000).
Reduced cell switching in a mobile computing en-
vironment. Proceedings of Sixth ACM International
Conference on Mobile Computing and Networking,
pages 143–154.
Castafieda-Camacho, J. and Lara-Rodriguez, D. (2000).
Performance of a new microcell/macrocell cellular ar-
chitecture with CDMA access. Vehicular Technology
Conference Proceedings, 1:483–486.
Chen, K.-C. (1994). Medium access control of wireless
LANs for mobile computing. IEEE Network, 8(5):50–
63.
Grossglauser, M. and David N. C. Tse (2002). Mobility
increases the capacity of Ad Hoc wireless networks.
IEEE/ACM Transactions on Networking, 10(4):477–
486.
Gupta, P. and Kumar, P. R. (2000). The capacity of wireless
networks. IEEE Transactions on Information Theory,
46(2):388–404.
Haartsen, J. and Ericsson Radio Systems B.V. (2000). The
bluetooth radio system. IEEE Personal Communica-
tions, 7(1):28–36.
I, C.-L., Greenstein, L. J., and Gitlin, R. D. (1993). A micro-
cell/macrocell cellular architecture for low- and high-
mobility wireless users. IEEE Journal on Selected Ar-
eas in Communications, 11(6):885–891.
Lee, W. C. Y. (1995). Mobile Cellular Telecommunication
System. Mcgraw-Hill.
Marcus, J. S. (2004). Call termination fees: The U.S. in
global perspective. Mannhein.
Robertson, N., Sanders, D., Seymour, P., and Thomas, R.
(1997). The four-color theorem. Journal of Combina-
torial Theory Series B, 70(1):2–44.
Schiller, J. (2000). Mobile Communications. Addison-
Wesley.
Siau, K. and Shen, Z. (2003). Mobile communications
and mobile services. International Journal of Mobile
Communications, 1(1/2):3–14.
Zigbee Alliance (2007). http://www.zigbee.org.
WINSYS 2007 - International Conference on Wireless Information Networks and Systems
50
