MATCHING FOR MOBILE USERS

IN THE PUBLISH/SUBSCRIBE PARADIGM

A. M. Roumani and D. B. Skillicorn

School of Computing, Queen’s University, Kingston, Canada

Keywords:

Mobile publish/subscribe, nearest neighbor problem, high-dimensional search, singular value decomposition.

Abstract:

In a mobile publish/subscribe paradigm, user service discovery and recommendation requires matching user

preferences with properties of published services. For example, a user may want to ﬁnd if there is a moderately

priced Chinese restaurant that does not require reservations close by. To generate accurate recommendations,

the properties of each user subscription must be matched with those of existing services as accurately as

possible. This isa difﬁcult problem when users are mobile, wirelessly connected to a network, and dynamically

roaming to different locations. The available data is very large, and the matching must be computed in real

time. Existing heuristics are quite ineffective.

We propose novel algorithms that use singular value decomposition as a dimension-reduction technique.

We introduce “positive” nearest-neighbor matching to ﬁnd services whose attribute values exceed those of

a new user subscription. Making this idea effective requires careful attention to details such as normaliza-

tion. Performance and quality of matches are reported for datasets representing applications in the mobile

publish/subscribe paradigm. For n services and m preference attributes, reasonable matches can be found in

time O (mlogn), using O (nm) storage.

1 INTRODUCTION

Publish/subscribe is an asynchronous messaging

paradigm for connecting information providers (pub-

lishers) with interested information consumers (sub-

scribers) in a distributed environment, providing a dy-

namic network topology and scalability. The pub/sub

paradigm extends, in a natural way, to other kinds

of service discovery, where service providers play the

role of publishers, and users with preferences are sub-

scribers. In a mobile setting, services are provided in

a geographical region, perhaps one cell of a mobile

phone system. Hence there are multiple pub/sub sys-

tems. Users’ service requests are contextualized by

and satisﬁed within the current region. User mobil-

ity implies that new service requests can appear at any

time, and that they must be satisﬁed quickly before the

user moves on. Either a push model or a pull model of

service is possible. In the pull model, a user requests a

matching service; in the push model, a service ﬁnds a

matching user preference and provides a service, per-

haps a discount coupon contextualized for the particu-

lar location of the user.

The central component of pub/sub systems is the

broker (event dispatcher), which facilitates the mes-

sage staging and routing in the system. Publishers

send information to the broker in the form of publica-

tions (events). Subscribers indicate interests in events

by maintaining a set of subscriptions at the broker.

They also indicate situations in which they would like

to be notiﬁed. The broker acts as a mediator between

publishers and subscribers, deciding when to send no-

tiﬁcations and who should receive them.

In a pub/sub paradigm, user service discovery re-

quires matching user preferences to available pub-

lished services in a timely fashion. Hence, the sys-

tem must ﬁnd an efﬁcient solution to the problem of

matching each subscription against a large number of

publications, or matching a publication (event) against

a large number of subscriptions. Take, for example,

a user with a handheld mobile device that uploads

his preference vector to an advertising server. The

server will match the preference vector with compa-

nies’ advertisements, and offers the user a coupon that

is valid for X time. Although there have been stud-

ies on matching algorithms in these systems, the prob-

lem of ﬁnding accurate matchings in a timely manner

amongst multiple possible publications is new.

This paper presents two efﬁcient matching algo-

rithms for mobile user services in pub/sub systems,

using Singular Value Decomposition (SVD) (Golub

and Loan, 1989) as a dimension reduction technique.

Known service (publication) data is transformed, in

a preprocessing stage, so that the high-dimensional

173

M. Roumani A. and B. Skillicorn D. (2007).

MATCHING FOR MOBILE USERS IN THE PUBLISH/SUBSCRIBE PARADIGM.

In Proceedings of the Second International Conference on Wireless Information Networks and Systems, pages 173-180

DOI: 10.5220/0002147401730180

 SciTePress

space of preferences for many possible services is pro-

jected into a low-dimensional space. When a match is

to be found, the user’s preferences are mapped into the

same low-dimensional space, producing values that

can be rapidly compared to available service proﬁles.

The ﬁrst algorithm implements this idea using a single

singular value decomposition, while the second uses

projections from randomly weighted versions of the

global preference data. We evaluate the performance

and quality of our algorithms using two datasets rep-

resenting applications in the mobile publish/subscribe

paradigm. In practice, reasonable matches can be

found in time

O (mlogn), using O (nm) storage space,

where n is the number of services (publications) and

m the number of attributes or preference possibilities.

This is in contrast to “approximate” nearest-neighbor

techniques, which require either time or storage expo-

nential in m.

2 EXISTING APPROACHES

There have been many designs proposed in the litera-

ture to model a pub/sub system. The earliest systems

were channel-based, with the broker component acting

as a broadcast channel (Babu and Widom, 2001). The

most signiﬁcant limitation of these systems is the lack

of ﬂexibility and expressiveness, leading to high net-

work trafﬁc, and necessitating additional subscriber-

side ﬁltering. A reﬁnement over the channel-based ap-

proach is the topic-based pub/sub model that catego-

rizes events into hierarchical subjects (topics), provid-

ing a ﬁner granularity of events (TIBCO, 2006). This

model uses a tree-like structure to categorize events,

and the matching process is basically a tree traversal.

The drawback of this model is the limited selectivity of

subscriptions. Today, companies like Netscape, Radio

Userland, and Moreover use RSS (RSS, 2006) to dis-

tribute and syndicate article summaries and headlines

to web users who wish to subscribe to them.

The latest pub/sub systems have the ability to ﬁlter

information using the contents of a published event. In

this model subscriptions are speciﬁed as expressions

evaluated over the published event contents. This ap-

proach provides greater expressiveness to ﬁlter publi-

cations and is more easily customized for individual

subscribers. The information ﬁltering process requires

an efﬁcient matching algorithm with high through-

put and scalability. Many algorithms proposed for

content-based matching (Fabret et al., 2001; Fabret

et al., 2000) attempt to optimize algorithms by limiting

the expressiveness of subscriptions.

There is also a proposed state-persistent model for

pub/sub systems (Leung, 2002) that stores the states

of both publications and subscriptions in the system

and notiﬁes subscribers only when the states of their

subscriptions change. An example of a content-based

matching algorithm for state-persistent pub/sub sys-

tems was proposed in (Leung and Jacobsen, 2003).

The matching problem in a state-persistent pub/sub

system requires storing information about publications

and subscriptions, indexing the relationships between

them, and detecting state transitions.

In this paper we are targeting users (subscribers)

who are mobile, with handheld devices, wirelessly

connected to a network, and dynamically roaming to

different environments. For mobile users, service dis-

covery requires matching user preferences to available

services as accurately as possible (For work on mo-

bile pub/sub see (Burcea et al., 2004)). This is a difﬁ-

cult problem since users are mobile and matches must

be done in real-time. The magnitude of the problem

increases with respect to the number of attributes in

the preference criteria for each user. Take, for exam-

ple, a user with a handheld mobile device who is in

Montreal and would like to eat Chinese food. Such

a user might submit a service request (subscription)

with the attributes: Chinese restaurant, Montreal, non-

smoking, within 15 minutes walking, under 10 min-

utes seating time, with buffet option, and below a cer-

tain price. In addition, there could be several possible

restaurants that match the user’s criteria, and we might

require the system to send one, some, or all of such

matches. The selection process in this environment

has to ﬁnd the best matching service(s) (a restaurant in

our example) that match the user’s request from among

many possible matches.

The values used for attributes can be classiﬁed into

two types as follows. Binary values (0 and 1), de-

scribing the presence or absence of particular prop-

erties of services that a user may require. For ex-

ample, a user may submit a subscription query for

weather reports consisting of the attributes (earth-

quakes, tsunamis, tornadoes, local weather, etc.). The

second type is ternary values (1, −1, and 0), describ-

ing a preference for or against a particular attribute, as

well as a neutral value. This could be, for example, the

restaurant property for “non-smoking”. There is little

point in trying for an absolute best ﬁt because the in-

formation available to the system can become stale, or

the user might change location. Such a dynamic envi-

ronment beneﬁts more from ﬁnding approximate best

matches instead.

3 THE NEAREST-NEIGHBOR

PROBLEM

Let the number of services be n and the number of at-

tributes be m. n could be in the thousands and m in the

WINSYS 2007 - International Conference on Wireless Information Networks and Systems

174

tens to hundreds. There is an obvious geometric inter-

pretation of the problem in which each service descrip-

tion tuple and each query (request) tuple are points in

an m-dimensional space.

When ﬁnding a match in the case of binary-valued

attributes, the goal is to ﬁnd the nearest neighbor of

the query tuple – but with the extra difﬁculty that the

value of each of the service-tuple attributes must be no

smaller than the value of the corresponding attribute

for the query. We refer to such a service tuple as fea-

sible. We are only interested in points that are fur-

ther away from the origin than the point correspond-

ing to the query, but we want to ﬁnd, among them,

the point that is nearest to the query. Call this the

“positive nearest-neighbor”. This guarantees that a

service tuple contains all the required preferences in

the query tuple (represented by ‘1’). In the case of

ternary-valued attributes, the goal is to ﬁnd the ordi-

nary nearest-neighbor of the query tuple, where the

match can be near to the query point in any direction.

Given a query tuple, there is an obvious brute-

force algorithm for ﬁnding the nearest neighbor with

time complexity

O (nm). For a small number of di-

mensions m, simple solutions sufﬁce, but for larger m,

say m > 10, the complexity of most methods grows

exponentially as a function of m. Dobkin and Lip-

ton (Dobkin and Lipton, 1976) give an upper bound

for the time required to search for a nearest neigh-

bor,

O (2

logn) query time, and O (n

m+1

) preprocess-

ing time and storage space. Most of the subsequent

improvements and extensions require a query time of

Ω( f(m)logn), where f(m) (sometimes hidden) de-

notes an exponential function of m. One of the most

widely used algorithms relies on the k-d tree (Samet,

1990). The average case analysis of heuristics using

k-d trees for ﬁxed dimension m requires

O (nlogn) for

preprocessing and

O (logn) query time. Although k-d

trees are efﬁcient in low dimensions, their query time

increases exponentially with increasing dimensional-

ity. The constant factors hidden in the asymptotic run-

ning time grow at least as fast as 2

, depending on the

distance metric used.

The complexity of exact nearest neighbor search

led to the “approximate” nearest-neighbor problem:

ﬁnding a point that may not be the nearest-neighbor to

the query point, but is not signiﬁcantly further away

from it than the true nearest neighbor. Several ap-

proximate nearest-neighbor algorithms have been de-

veloped (Kleinberg, 1997)but they either use substan-

tial storage space, or have poor performance when

the number of dimensions is greater than logn. The

positive-nearest-neighbor requirement means that the

performance of such algorithms becomes even worse.

For example, the positive nearest neighbor may be

quite far from the query point, with many closer but

infeasible objects (service tuples). This suggests using

a technique that can transform the high-dimensional

space of the data into lower-dimensional subspaces.

One obvious technique is Singular Value Decomposi-

tion (SVD). We have already noted the natural geomet-

ric interpretation of a list of tuples describing services.

If we regard such a list as an n× m matrix, then a sin-

gular value decomposition can be regarded as trans-

forming the original geometric space into a new one

with the following useful property: the ﬁrst axis of the

new space points along the direction of maximal vari-

ation in the original data; the second axis along the di-

rection of maximal variation remaining, and so on. Let

A be the n× m matrix representing the services. Then

the singular value decomposition of matrix A is given

by A = USV

where

indicates matrix transpose. If

matrix A has r linearly-independent columns (r is the

rank of A), then U is an n × r orthogonal matrix (i.e.,

U = I), S is an r × r non-negative diagonal ma-

trix whose elements (called singular values) are non-

increasing, s

≥ s

> 0, and V

is an orthogonal

r × m matrix. Each row of U gives the coordinates of

the corresponding row of A in the coordinate system of

the new axes (deﬁned by V). The complexity of com-

puting the SVD of a matrix is

O (n

m) and the space

required to store the data structure is

O (mr+ r

+ rn).

One of the most useful properties of an SVD is that

the matrices on the right-hand side can be truncated by

choosing the k largest singular values and the corre-

sponding k columns of U and k rows of V

. We show

that a tuple of m properties can be encoded by coordi-

nates in a single dimension using SVD, given suitable

normalization of the data. Matching a query tuple to

appropriate service tuples requires encoding the query

attributes, and then searching a ranked list of projected

service values. We also propose a technique that pro-

duces highly accurate matches by using a collection

of SVD decompositions, in which each decomposition

uses data independently weighted by random scalars.

This provides several different projections of the data,

which tends to reveal the most important latent struc-

ture. Hereafter we will refer to nearest-neighbor as

n-n.

4 ALGORITHMS

We propose two SVD-based Search (SVDS) tech-

niques for solving the positive and the ordinary n-n

matching problem: basic SVDS (bSVDS) and random-

weighted SVDS (rwSVDS). The bSVDS algorithm

works in two stages: a preprocessing stage and a run-

time stage. The natural similarity (proximity) metric

is Euclidean distance – a service tuple is a good match

for a request tuple if the Euclidean distance between

MATCHING FOR MOBILE USERS IN THE PUBLISH/SUBSCRIBE PARADIGM

175

them is small (and the service-tuple attributes meet or

exceed the request requirements in the original space

for the positive n-n case). We ﬁrst preprocess the set

of service tuples by computing the SVD of the origi-

nal matrix A after normalization, then truncate the re-

sult to one dimension. The resulting list is sorted by

increasing values of u

, the ﬁrst column of U. When

a new query arrives, it must be mapped into the cor-

responding space of U, and a value created that can

be compared to the encoded values. By re-arranging

the SVD decomposition equation we get U = AVS

−1

This multiplication can be applied to new queries with

the shape of rows of A to compute their coordinates

in the transformed space. Since we have truncated the

SVD, this mapping requires only the ﬁrst column of

V and the ﬁrst singular value, and therefore takes time

O (m). After the transformation maps the query tuple

to a single value, the value is compared to service’ val-

ues using binary search to ﬁnd the service with the

closest value. This service tuple may not be feasible

(it is similar to the query tuple in the original A matrix

but one or more of its attributes is smaller than the cor-

responding value of the query). In this case, the ranked

list is searched by choosing the next closest value on

either side of the original entry, until a feasible tuple is

found.

Algorithm rwSVDS is an extension of bSVDS; in-

stead of using a single search list to predict the pos-

itive n-n point, it uses multiple search lists. rwSVDS

uses a set of three decision lists to predict the nearest-

neighbor point. To create each list, the attributes of the

original dataset are weighted with different (randomly

chosen) scalars in the range (0,1] to create a new

weighted matrix (note that the original input data is

not changed, since is later used for feasibility check).

This process is repeated three times to generate three

differently weighted matrices. SVD is then applied

to each matrix independently, to generate three one-

dimensional spaces, which are then each sorted. The

selection process transforms each query tuple (after

scaling it with the corresponding weight vector) into

the space of each SVD, then searches all three ranked

lists in a concurrent fashion to ﬁnd a common match.

The ﬁrst feasible service-tuple to have been found on

all three lists is reported as the best match. The use of

three lists is based on extensive experiments that show

that more lists adds cost without improving matches.

5 EXPERIMENTAL SETTING

We generate artiﬁcial datasets to represent proper-

ties of services in the pub/sub paradigm, with binary-

valued attributes (selected randomly with 20% den-

sity of 1’s) and ternary-valued attributes (selected uni-

formly randomly). We normalize the data by zero-

centering each column. Each experiment result is the

average of 70 runs. For comparison purposes, we also

consider a ranking algorithm that uses the sum of the

attributes. We call it the SUM-based Search algorithm

(SUMS). The advantage of the sum is that any service

tuple whose sum is smaller than the sum of the require-

ments of a query tuple cannot possibly be feasible. We

compute the sum of attributes for each service tuple

and sort the list based on the sum of ratings. The

sum is then computed for each query tuple, and bi-

nary search is used to ﬁnd the feasible service closest

in sum to it. When applying the SUMS algorithm to

the ternary-valued data, there is a special handling to

accommodate for the negative values (−1’s); the sum

is computed by ﬁrst incrementing the attributes’ val-

ues. The same handling is done for the queries before

the search starts.

Both our SVDS algorithms and SUMS algorithm

have similar properties: both require

O (nm) storage

for the ranking information (since the full set of at-

tributes must be checked for feasibility); for both, the

cost of binary search is

O (logn); and for both the cost

of computing the ﬁt between a query tuple and a ser-

vice tuple is

O (m). The preprocessing required for

SVDS is more expensive. However, this cost is amor-

tized over all the matches of queries to services. The

performance difference between the two rankings de-

pends on how many list elements must be examined

to ﬁnd a feasible match, and on the quality of such a

match. We also compare our algorithms’ effectiveness

with that of randomly selecting services until a feasi-

ble one is found (call this simple algorithm RAND),

and with exhaustive search. RAND provides a base-

line for the number of probes required to ﬁnd a good

solution, while exhaustive search provides a baseline

for how good a solution is possible.

The main performance measures of interest are:

cost – measured in number of probes needed to ﬁnd

a match, including the cost of binary search (where

applicable); sub-quality – the Euclidean distance

from the match point found by the algorithm to the

query point (A higher value represents a lower-quality

match; and sub-optimality ratio – the ratio of the so-

lution found by an algorithm to the optimal solution.

The lower the value the better the quality of the match

found.

In our experiments, we search for the positive n-n

in binary-valued datasets, and for the ordinary n-n in

ternary-valued datasets. For each combination of ex-

periments, the fraction of objects that are feasible for

each query are held to approximately 5%. If feasible

objects are extremely scarce, then exhaustive search is

probably the best matching technique; if the fraction

of feasible objects is large, then the system does not

WINSYS 2007 - International Conference on Wireless Information Networks and Systems

176

provide much discrimination in services which is also

an unlikely scenario.

6 RESULTS AND DISCUSSION

We study the effect of varying the number of objects

(services) and attributes on the search cost and quality

of the solutions.

6.1 Binary-valued Datasets

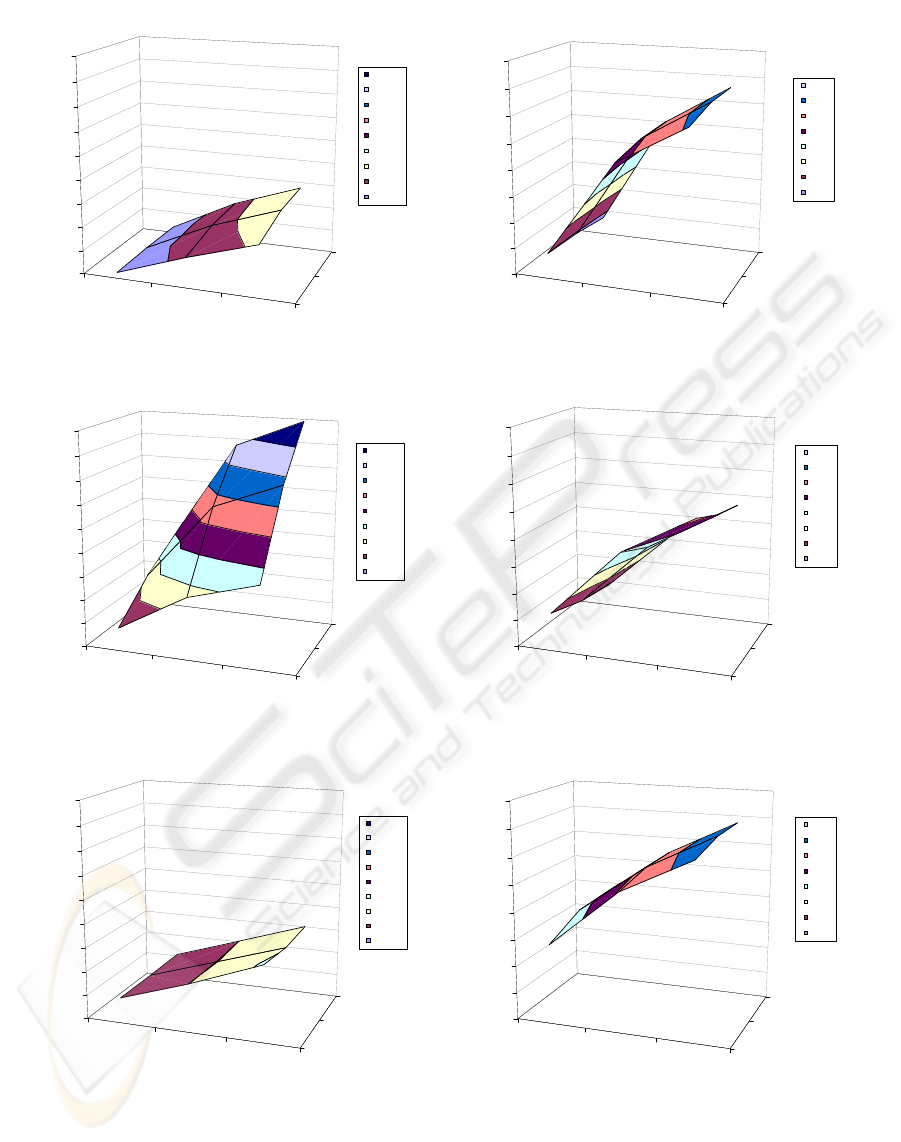
First, we test the basic SVDS algorithm (bSVDS). Fig-

ure 1 plots the number of probes (cost) required to ﬁnd

a feasible object for a query (left column), and the sub-

quality of this match (right column) when attributes

are binary values. Plots (a) and (b) show the number of

probes required and the sub-quality for bSVDS, plots

(f) show them for RAND.

We see in Figure 1 that bSVDS requires the low-

est number of probes to ﬁnd a match. Although the

cost and sub-quality of the match found by all al-

gorithms increases with increasing numbers of ob-

jects and attributes, the number of probes required

by SUMS increases rapidly. However, this increase

comes at a tradeoff with sub-quality. Nevertheless,

for what might be considered the most practical cases,

i.e., those where the number of attributes is relatively

small, bSVDS is a clear winner in both cost and quality

of matches. bSVDS requires, on average, only 11% of

the probes of SUMS, and ﬁnds better-quality matches

that are 78% of the sub-quality of SUMS.

In comparison to RAND, algorithm bSVDS re-

quires 77% of the probes that RAND requires, espe-

cially for small numbers of attributes, and ﬁnds better-

quality matches that are 38% of the sub-quality of

RAND, for a moderate number of attributes. On the

other hand, SUMS requires many more probes than

RAND in almost all settings, except for small numbers

of objects and attributes. This comes at a tradeoff with

match quality for all parameter settings. Although the

sub-quality of bSVDS increases with the number of at-

tributes, it actually gets closer to the optimal solution,

as shown in Figure 2.

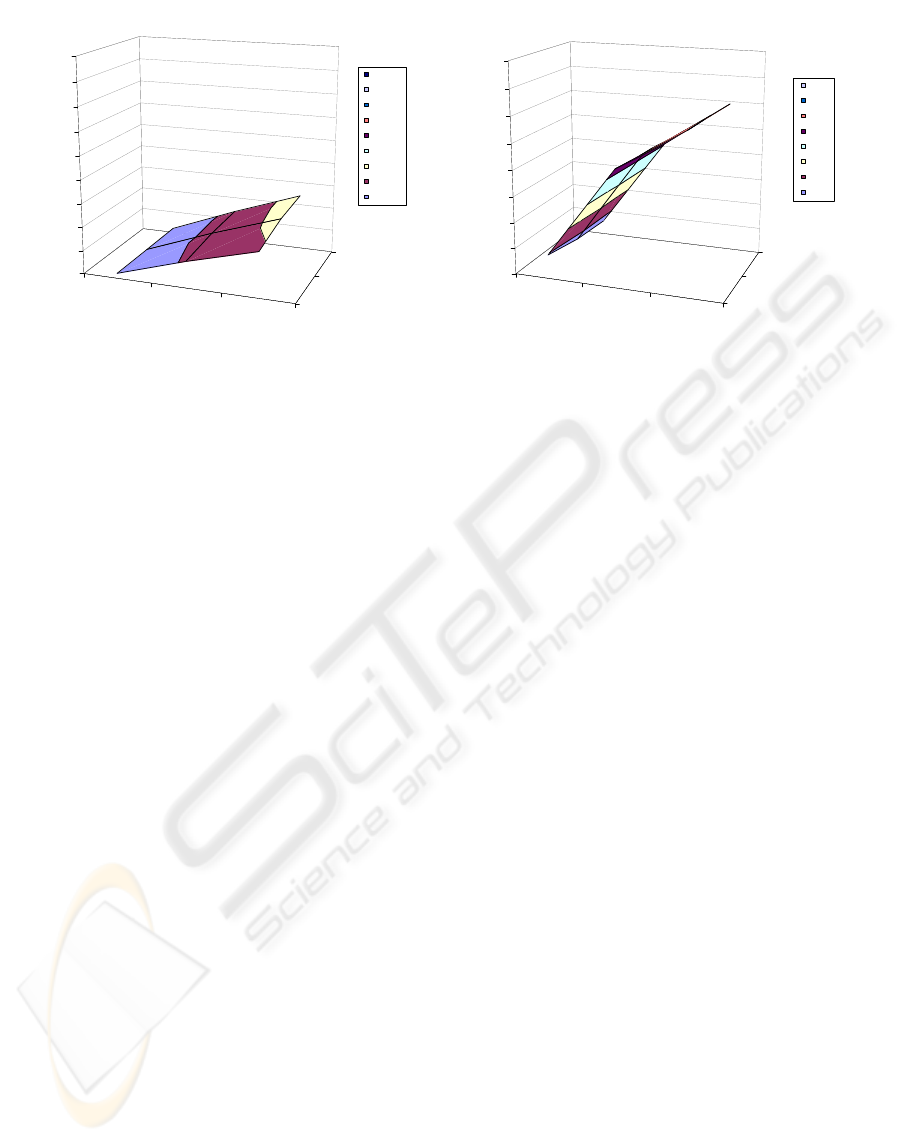
Figure 3 plots the number of probes (left column)

and the sub-quality (right column) for (rwSVDS).

It achieves better performance and better-quality

matches than bSVDS for all parameter settings – an

average of 19% lower probes and 10% better qual-

ity. This improvement affects, in its turn, the cost and

quality ratios to SUMS and RAND. Algorithm rwSVDS

now requires, on average, only 15% of the probes

of SUMS, and ﬁnds slightly better-quality matches,

of 94% the sub-quality of matches found by SUMS,

100

500

1000

Sub

Optimality

Ratio

Attributes

O bjects

bSVDS

10-11

9-10

8-9

7-8

6-7

5-6

4-5

3-4

2-3

1-2

Figure 2: Positive n-n in binary-valued dataset: bSVDS sub-

optimality ratio.

with the best results observed for small numbers of at-

tributes. As for RAND, rwSVDS requires only 33%

as many probes, and ﬁnds better-quality matches of

40% the sub-quality of those found by RAND. Fig-

ure 3(b) shows that the sub-quality of the match found

by rwSVDS increases with increasing numbers of at-

tributes, but starts to plateau as these become large.

Algorithm rwSVDS ﬁnds the best-quality matches

with better overall performance than bSVDS. Com-

pared to SUMS, it also achieved, by far, lower search

cost and better match quality for small numbers of

attributes. For higher numbers of attributes, it still

achieved near-optimal results.

6.2 Ternary-Valued Datasets

Figure 4 plots the number of probes required by al-

gorithm (bSVDS) to ﬁnd a match (ordinary n-n) for

each query, and the sub-quality of this match when at-

tributes are ternary values.

Figure 4 shows that, in comparison to the positive

n-n case, algorithms bSVDS and SUMS require many

fewer probes to ﬁnd a match when the feasibility con-

dition is relaxed, whereas RAND, by deﬁnition, takes

only one probe. SUMS requires slightly more probes

than random matching (mainly due to the overhead of

the initial binary search) but maintains almost constant

cost. Algorithm bSVDS comes last in terms of per-

formance, with slightly more probes than SUMS, but

only a constant number of probes are required after

the binary search (see Figure 4(a)). As for the qual-

ity of the solution, bSVDS ﬁnds better-quality matches

than SUMS and RAND – an average of 67% of the

sub-quality of SUMS, and 64% of the sub-quality of

RAND, with the best quality for small numbers of at-

tributes.

Algorithm rwSVDS results are shown in Figure ??.

rwSVDS requires more probes than bSVDS but, on

MATCHING FOR MOBILE USERS IN THE PUBLISH/SUBSCRIBE PARADIGM

177

100

500

1000

500

1000

1500

2000

2500

3000

3500

4000

4500

Cost

Attributes

O bjects

bSVDS

4000-4500

3500-4000

3000-3500

2500-3000

2000-2500

1500-2000

1000-1500

500-1000

0-500

(a)

100

500

1000

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

Sub

Quality

Attributes

O bjects

bSVDS

3.5-4.0

3.0-3.5

2.5-3.0

2.0-2.5

1.5-2.0

1.0-1.5

0.5-1.0

0.0-0.5

(b)

100

500

1000

500

1000

1500

2000

2500

3000

3500

4000

4500

Cost

Attributes

Items

SUMS

4000-4500

3500-4000

3000-3500

2500-3000

2000-2500

1500-2000

1000-1500

500-1000

0-500

(c)

100

500

1000

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

Sub

Quality

Attributes

O bjects

SUMS

3.5-4.0

3.0-3.5

2.5-3.0

2.0-2.5

1.5-2.0

1.0-1.5

0.5-1.0

0.0-0.5

(d)

100

500

1000

500

1000

1500

2000

2500

3000

3500

4000

4500

Cost

Attributes

O bjects

RAND

4000-4500

3500-4000

3000-3500

2500-3000

2000-2500

1500-2000

1000-1500

500-1000

0-500

(e)

100

500

1000

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

Sub

Quality

Attributes

O bjects

RAND

3.5-4.0

3.0-3.5

2.5-3.0

2.0-2.5

1.5-2.0

1.0-1.5

0.5-1.0

0.0-0.5

(f)

Figure 1: Positive n-n in binary-valued dataset: Search cost and sub-quality for: (a) and (b) bSVDS, (c) and (d) SUMS, (e) and

(f) RAND.

the other hand, it ﬁnds matches of twice the quality.

This improvement in match quality, consequently, af-

fects the quality ratios to matches found by SUMS and

RAND, with more emphasis on the tradeoff between

search cost and match quality.

It is not so obvious which algorithm is best in terms

of cost and quality; bSVDS has slightly worse perfor-

mance than SUMS and RAND, but it achieves better

WINSYS 2007 - International Conference on Wireless Information Networks and Systems

178

100

500

1000

500

1000

1500

2000

2500

3000

3500

4000

4500

Cost

Attributes

O bjects

rwSVDS

4000-4500

3500-4000

3000-3500

2500-3000

2000-2500

1500-2000

1000-1500

500-1000

0-500

(a) Cost

100

500

1000

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

Sub

Quality

Attributes

O bjects

rwSVDS

3.5-4.0

3.0-3.5

2.5-3.0

2.0-2.5

1.5-2.0

1.0-1.5

0.5-1.0

0.0-0.5

(b) Sub-quality

Figure 3: Positive n-n in binary-valued dataset: Search cost and sub-quality for rwSVDS.

match quality, which would justify some sacriﬁce in

performance. Relative to rwSVDS, the tradeoff on per-

formance and quality is much more apparent. Algo-

rithm bSVDS has better performance, but lower match

quality.

7 CONCLUSIONS

One of the critical research challenges in the devel-

opment of pub/sub systems that support services for

mobile-user interactive applications is the discovery

of an efﬁcient matching algorithm that is scalable

and reasonably effective, and provides good matches

between user requests and available services. As

the number of services and their attributes increase,

solutions that are cheap to implement are required.

We have presented two projection and search tech-

niques based on SVD, using SVD as a preprocessing

step to project service properties into low-dimensional

spaces. Careful normalization, and the use of multiple

projections based on random weighting of attributes

result in one-dimensional lists that can be searched,

in practice, in only a constant number of probes be-

yond the basic binary search required to ﬁnd the right

part of the list. The overall complexity of matching is

O (mlogn) time and O (nm) storage space.

REFERENCES

Babu, S. and Widom, J. (2001). Continuous queries over

data streams. In ACM SIGMOD, pages 109–120, NY,

USA.

Burcea, I., Jacobsen, H.-A., DeLara, E., Muthusam, V., and

Petrovic, M. (2004). Disconnected operations in pub-

lish/subscribe. In IEEE MDM, pages 39–50, CA, USA.

Dobkin, D. and Lipton, R. (1976). Multidimensional search

problems. SIAM Journal on Computing, 5:181–186.

Fabret, F., Jacobsen, H.-A., Llirbat, F., Pereira, J., Ross,

K. A., and Shasha, D. (2001). Filtering algorithms and

implementation for very fast publish/subscribe sys-

tems. In ACM SIGMOD, pages 115–126, CA, USA.

Fabret, F., Llirbat, F., Pereira, J., and Shasha, D.

(2000). Efﬁcient matching for content-based pub-

lish/subscribe systems. Technical report, INRIA.

http://wwwcaravel.inria.fr/pereira/matching.ps.

Golub, G. H. and Loan, C. F. V. (1989). Matrix Computa-

tions. Johns Hopkins Press, MD, USA.

Kleinberg, J. (1997). Two algorithms for nearest-neighbour

search in high dimensions. In 29th ACM STOC, pages

599–608.

Leung, H. (2002). Subject space: A state-persistent model

for publish/subscribe systems. In CASCON, pages 7–

17, Toronto, Canada.

Leung, H. and Jacobsen, H.-A. (2003). Efﬁcient matching

for state-persistent publish/subscribe systems. In CAS-

CON, pages 182–196, Toronto, Canada.

RSS (2006). RSS: RDF site summary.

www-106.ibm.com/

developerworks/library/w-rss.html?dwzone=

web

Samet, H. (1990). The Design and Analysis of Spatial Data

Structures. Addison-Wesley, Boston, MA, USA.

TIBCO (2006). TIBCO rendezvous.

www.tibco.com/

software/messaging/rendezvous.jsp

MATCHING FOR MOBILE USERS IN THE PUBLISH/SUBSCRIBE PARADIGM

179

100

500

1000

Cost

Attributes

O bjects

bSVDS

0-1 1-2

2-3 3-4

4-5 5-6

6-7 7-8

8-9 9-10

(a)

100

500

1000

Sub

Quality

Attributes

O bjects

bSVDS

0-1 1-2

2-3 3-4

4-5 5-6

6-7 7-8

8-9 9-10

(b)

100

500

1000

Cost

Attributes

O bjects

SUMS

0-1 1-2

2-3 3-4

4-5 5-6

6-7 7-8

8-9 9-10

(c)

100

500

1000

Sub

Quality

Attributes

O bjects

SUMS

0-1 1-2

2-3 3-4

4-5 5-6

6-7 7-8

8-9 9-10

(d)

100

500

1000

Cost

Attributes

O bjects

RAND

0-1 1-2

2-3 3-4

4-5 5-6

6-7 7-8

8-9 9-10

(e)

100

500

1000

Sub

Quality

Attributes

O bjects

RAND

0-1 1-2

2-3 3-4

4-5 5-6

6-7 7-8

8-9 9-10

(f)

Figure 4: Ordinary n-n in ternary-valued dataset: Search cost and sub-quality for: (a) and (b) bSVDS, (c) and (d) SUMS, (e)

and (f) RAND.

WINSYS 2007 - International Conference on Wireless Information Networks and Systems

180