A NEW FUZZY LOGIC CONTROLLER FOR TRADING

ON THE STOCK MARKET

Francesco Maria Raimondi, Salvatore Pennacchio

Dipartimento di Ingegneria dell’Automazione e dei Sistemi

University of Palermo, Viale delle Scienze, 90128, Palermo, Italy

Pietro Via, Marianna Mulè

Former Sudents at University Of Palermo, Engineering Faculty

University of Palermo, Viale delle Scienze, 90128, Palermo, Italy

Keywords: Trading Systems, Fuzzy Logic, Genetic Algorithms, Mib30, Technical Analysis.

Abstract: A common problem that financial operators often meet in their own work is to make, at the right moment,

the operational choices on the Stock Market. Once the Market to act on has been chosen, the financial

operator has to decide when and how to operate on it, in order to achieve a profit. The problem that we are

going to deal with is the planning of an automatic decisional system for the management of long positions

on bull market. First, a trading system (TS) will be implemented pointing its features out. Then a fuzzy logic

implementation of the TS will be introduced (FTS). The fuzzy system will be optimized by the genetic

algorithms. Finally, the two different implementations of the trading system will be compared using some

performance indexes.

1 INTRODUCTION

Different ways exist to operate on the Stock Market:

following the instinct or smell, reading journals and

reports, with the help of experts, or applying more

methodic techniques. Among all the available

operational techniques, there are the technical

analysis (Edwards, Magee, 1957) and fundamental

analysis (Schwager, 1995). Furthermore, in the last

years some experimental techniques has been used.

These techniques are founded upon the concepts of

soft computing. Some of them simulate the process

of the human reasoning (expert systems and fuzzy

systems), others the biological operation of the brain

(neural networks) and others the genetic evolution

(genetic algorithms). All these techniques can leave

out the principles of technical analysis and

fundamental analysis, but they can use them

partially (G.J. Deboeck, 1994).

In Li, Xiong (2005), the authors presents a fuzzy

neural network to predict the comprehensive index

of Shanghai stock market

. In Hiemstra (1994), the

author presents a general approach to stock market

prediction and introduces an architecture of a fuzzy

logic forecasting support system. In Setness, van

Drempt, (1999) the authors examine the application

of other fuzzy models to the problem of stock

market analysis. In H.S. Ng, K.P. Lam a Genetic

Fuzzy Expert Trading System (GFETS) was

designed to simulate the vague and fuzzy trading

rules and give the buy-sell signal. Fuzzy trading

rules are optimized and selected using genetic

algorithm in GFETS. In H. Dourra, P. Siy (2002) the

authors proposed a method to map some technical

indicators into new inputs that can be fed into a

fuzzy logic system.

In this paper, in the section 2, we shall introduce

the classical methodologies of analysis of the Stock

Market and the trading systems. In the section 3, the

implementation of a trading system on the Mib30

(TS) is introduced. In the section 4 we shall

introduce the fuzzy logic, used for the

implementation of the fuzzy trading system (FTS).

In the section 5, a comparative analysis of the two

systems is effected through some performance

indexes.

322

Maria Raimondi F., Pennacchio S., Via P. and Mulè M. (2007).

A NEW FUZZY LOGIC CONTROLLER FOR TRADING ON THE STOCK MARKET.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 322-329

DOI: 10.5220/0002345803220329

 SciTePress

2 ANALYSIS OF THE STOCK

MARKET

2.1 Technical Analysis

The economic phenomena and their reflexes on the

Stock Market are very complicated. The most

important branch of research is technical analysis.

(Malkiel, 1981; Fama, 1989).

Technical analysis mainly founds itself on the

observation of the prices (Edwards, Magee, 1957).

Technical analysis identifies the direction of a trend

and indicates, at the right moment, when the trend

direction is changing. In order to do this it uses the

graphic and algorithmic tools which are indicators,

defined as functions of prices and volumes (Elder,

1993; Sack, 1992).

The most diffused tools of technical analysis are

algorithmic (indicators and oscillators) (Malkiel,

1981; Edwards, Magee, 1957). The indicators and

the oscillators offer a different perspective from

which to analyze the price action. They are derived

by applying a formula to the price data of a security.

Price data includes any combination of the open,

high, low or close over a period of time. An

oscillator is an indicator that fluctuates above and

below a centerline or between set levels as its value

changes over time (Edwards, Magee, 1957).

Below, we shall describe the features of some

principal indicators, which will be used in this

research.

2.1.1 MACD (Moving Average

Convergence/Divergence)

The MACD is a momentum oscillator, i.e. it

measures the strength of the price movement. The

MACD is calculated by subtracting the value of a

0.075 (26-period) exponential moving average from

a 0.15 (12-period) exponential moving average. A 9-

period exponential moving average of the MACD,

called trigger line, is used to signal buy orders or

sell orders.

2.1.2 ADX (Average Directional Movement

Index)

The ADX, built by Wilder's smoothing of the DX

(Directional Movement Index), measures the

strength of a trend and it is useful to individualize

the shift from a trend phase to a congestion phase

(Hartle, 1991). The DX characterizes the directional

movement of the prices and oscillates between 0 and

100 (then also the ADX oscillates between 0 and

100). The values of the ADX, that overcomes a

certain threshold (the select values usually go from

20 to 40), point out a strong trend phase, while

values that go under the threshold point out a

congestion phase.

2.2 Trading Systems

The expression "trading system”, as is known,

characterizes a rigorous methodology that uses fixed

rules (trading rules) to decide how to operate on the

Stock Market. The aim of the trading system is

realizing, through a particular strategy, good profits

for the investor (trader).

The trading systems are usually implemented to

use, at the same time, several tools of technical

analysis. The contemporary use of these tools can

produce discordant results. This problem can be

solved using a computational algorithm that

produces buy signals and sell signals when the

available data are compatible with all of the

established rules.

2.2.1 Evaluation of a Trading System

Once that the trading system has been well defined,

there are different criterions with which to appraise

the success or the failure of it. The most important

tools, predisposed to evaluate the efficiency of a

trading system and used in this research, are

described below (Elder, 1993).

1) The Equity Line is probably the best

diagnostic tool for trading system developer. In one

graph it shows the sum total of the success or failure

of the system being tested, and the resulting effect

on your equity. The ideal chart of an equity line

should be an increasing curve; if so, there would be

constant and increasing profits from time to time.

2) The Profit is the aggregate clean profit and

it’s achieved supposing to close one’s own positions

the last day of the simulation.

3) The Profit / Loss Index compares the profit

produced by the winning operations to that produced

by the lost operations:

Profit Trade

Profit

Index P/L =

where the Trade Profit is the profit obtained by the

winning operations only.

4) The Reward/Risk Index is defined as

A NEW FUZZY LOGIC CONTROLLER FOR TRADING ON THE STOCK MARKET

323

Risk

Reward

Index R/R =

where the Reward is the aggregate clean profit

(Profit) and the Risk is the lowest point, of equity

line. If this index is smaller than +50, we submit the

trader to a too elevated stress compared to the profits

produced by the trading system.

5) The Buy & Hold Index compares the profit

obtained by the trading system to that obtained by

the strategy Buy & Hold. It consists in opening a

long position (buy order) the first day of the

simulation and in closing such position (sell order)

the last day, without effecting any operations during

the select period.

6) The Win/Lose Index corresponds to the ratio

between winning operations and lost operations

operationsLost N

operations WinningN

Index W/L

3 A TRADING SYSTEM ON

MIB30

In this section we shall introduce the design of a

trading system (TS), which is the base for the

following development of a fuzzy trading system

(FTS). Working with FTS, we will be able to apply

our algorithmic trading rules using the peculiar

properties of fuzzy logic. Before going deep into the

development of TS, we have to introduce the time

series of prices on which the TS has been applied.

3.1 The Time Series

We have chosen the Italian Stock Market and the

security of the Mib30 (Milan Italy Stock Exchange

30 Index), based on the 30 leading stocks, that is, the

most liquid and most highly capitalized stocks listed

on the Italian Stock Exchange. The time series of

Mib30 (Figure 1) has been downloaded from Yahoo.

Figure 1: Close prices of MIB30.

Before using the time series, we have integrated

some lacking data, using a linear interpolation. The

used time series is characterized by a daily

frequency, from 03/01/2000 to 07/07/2006, and

every sample is made of the open price, of the

maximum price, of the minimum price and of the

close price of the day (1690 samples).

3.2 Trading Rules

The system has been designed only for the

management of long positions in bull market. It

produces buy signals in bull market and sell signals

in bear market. Furthermore, we didn’t take into

accounts the criterions for the management of not

sustainable losses or of gains higher than fixed

profit.

We have decided to individualize three possible

market phases: the bull market, bear market and the

congested market. Moreover, considering that in the

bull market and in the bear market we can apply the

same operational tools, we have focused on the

identification of only two of the market phases: the

trend market (whether it is bull market or it is bear

market) and the congested market. The TS has an

initial filter which allows it to establish, with a

certain degree of approximation, the type of market

phases. To detect the type of market phases we have

chosen the ADX. The identification between the

trend markets and congested market has been made

through a threshold. If the ADX is lower than the

threshold (congested market), the TS doesn't

produce any BUY or SELL signals, but WAIT

signal (no signal). If the ADX is higher than the

threshold (trend market) instead, the TS uses the

MACD oscillator (jointly the trigger line) to produce

operational signals according to the following rule: a

SELL signal occurs when the MACD falls below its

trigger line; a BUY signal occurs when the MACD

rises above its trigger line. When the trigger line

stays below (or above) the MACD, the TS produces

a WAIT signal. The TS is not a very aggressive

system but surely it is a solid one.

3.3 Parameters Tuning

Firstly, we must fit the ADX period: a very wide

ADX period implicates a slow movement of this

indicator; while a narrow ADX period determines a

rapid movement of this indicator. In addition, we

must fit a second parameter, the ADX threshold (this

parameter determines the ADX sensibility).

ICEIS 2007 - International Conference on Enterprise Information Systems

324

In relation to the trigger line, we have chosen a

standard period of 9 days; therefore, we must tune

only the first two parameters.

The most logical method for the choice of values

of the ADX period and the ADX threshold is

selecting those values which had previously

produced the best results. First, we have specified a

allowable range for parameters value; then we have

simulated all possible trading systems from

03/01/2000 to 26/04/2004 (two-third of the time

series); subsequently, we have saved the parameters

value that have produced the best results (maximum

clean profit). We have finally used the best

parameters value to test the TS from 27/04/2004 to

07/07/2006 (the rest one-third of the time series).

The trading system that has produced the best

clean profit had the ADX period equal to 7 and the

ADX threshold equal to 23.

3.4 System Evaluation

The TS, applied from 03/01/2000 to 07/07/06, have

generated 45 buy signals and the same number of

sell signals with a clean profit equal to 18399 (unit

price). Buy and sell signals are uniformly distributed

within six years taken for the simulation. So we

can’t observe any period of inactivity of the system,

even if our system shows the tendency to signal the

operations lately. The system is not able to exploit

fully the bull market phases and, at the same time, it

follows the bear market phases for a too long time.

This is due to the characteristics of the instruments

of technical analysis we applied. Observing the trend

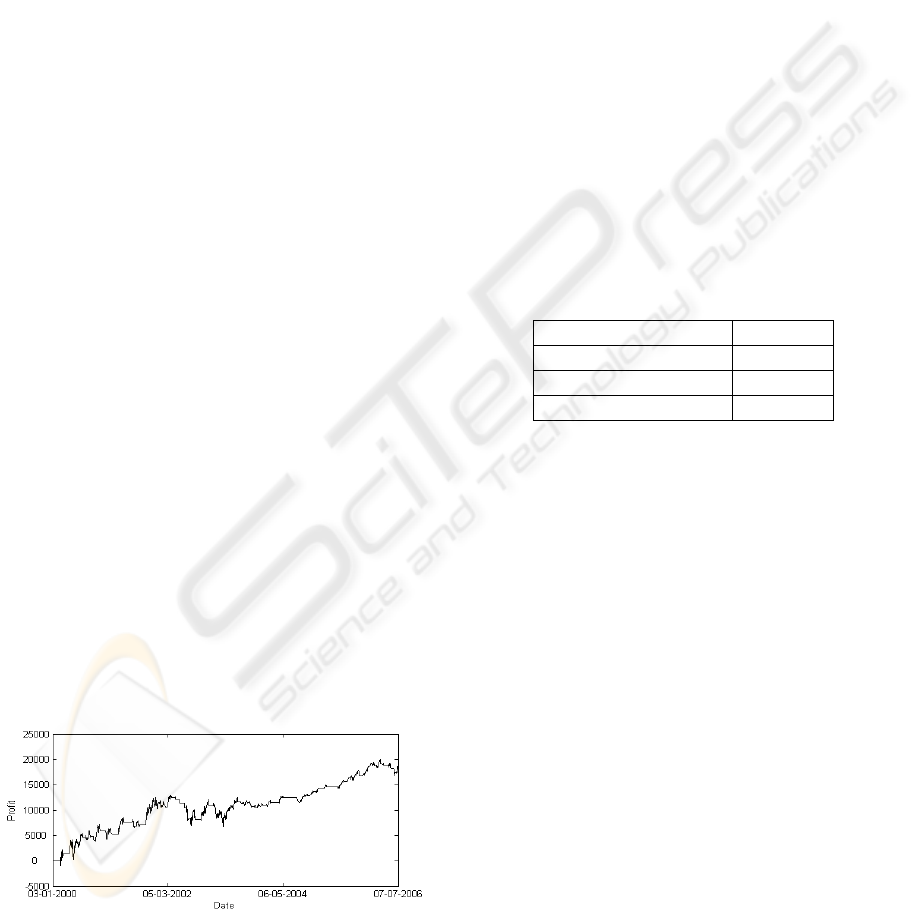
of the system equity line (Figure 2) we can notice

that the curve is characterized by growing steps in

bull markets and horizontal lines in bear markets.

Our system aims to improve profits taking advantage

of upwards trends and to limit losses during

downwards trends.

Figure 2: Equity Line of TS.

However we can also notice some periods in which

the system has to face some losses because of the

decision to maintain the actual position (WAIT)

even during a congestion phase. Finally, we have to

point out that we have ignored the costs of all the

transactions (both for opening and closing

operations). That is the costs to open and to close an

operation don’t affect on the whole profit.

As regards performance indexes, (Table 1), we

can notice that:

 the Profit/Loss Index, greater than 50, indicates

that, during the six years used for simulation,

profits have been greater than losses;

 the Reward/Risk Index, extremely near to 100,

allows us to state that the system made profits

with a very low risk factor;

 very high value of the Buy & Hold Index

assures us that our system is a useful trading

system;

 the Win/Lose Index, greater than 1, indicates

that we made a number of winning deals

greater than the number of losing ones.

Table 1: Performance Indexes.

Profit/Loss Index 60.30

Reward/Risk Index 95.30

Buy & Hold Index 280.04

Win/Lose Index 1.37

4 A FUZZY TRADING SYSTEM

ON MIB30

4.1 The Fuzzy Logic and the Stock

Market

The studying and forecasting of stock markets often

involve vague and inaccurate concepts and

reasoning. Fuzzy logic appears as the most natural

tool to face this kind of problems, since it has been

designed just to represent uncertain knowledge

(Zadeh, 1978; Yager, Zadeh, 1992). The application

of fuzzy logic in the economic-financial field allows

to implement a simple system, whose operations are

easy to guess. Furthermore, a good trading system

needs the support of a suitable model that allows (Li,

Xiong, 2005; Hiemstra, 1994; Setness, Van Drempt,

1999):

 to define and store all the information suitable

for the desired forecast;

 to represent the uncertainty and the

imperfection that characterize the information

A NEW FUZZY LOGIC CONTROLLER FOR TRADING ON THE STOCK MARKET

325

that belongs to the experts of this sector;

 to provide a clear, explanatory and interactive

forecast.

Fuzzy logic allows to represent these concepts and

to synthesize them in the implementation of a fuzzy

controller that can replace a classical trading system.

4.2 The Fuzzy Logic Controller

In this section, we shall introduce the fuzzy

controller designed to implement the FTS. The FTS,

like the TS, is a system designed only for the

management of long positions in bull markets. It

produces BUY signals in bull markets and SELL

signals in bear markets. Our controller is

characterized by three inputs (ADX, perMT1,

perMT2) and only one output.

Respective membership functions (MF) are

associated to all the variables (Zadeh, 1975;

Mamdani, Assilian, 1975; King, Mamdani, 1967).

For every MF, we have determined their own

parameters through Genetic Algorithms (GA)

(Davis, 1991; Goldberg, 1989), using as fitness the

profit obtained applying the systems to the whole

historical data series. We have implemented a

customized function in order to create our

individuals (our initial population was made up of

50 individuals, each of which represents a set of

parameters). Also we have implemented two

functions to realize, during optimization, the

crossover and the mutation process to generate new

individuals through evolution. In this way, we have

deleted the complex and hard-working phase of

manual definition of the parameters (Karr, Gentry,

1993) and we have also easily detected the most

correct shapes of the various MF. Moreover we’ve

been able to impose and to respect some ties on the

mutual positions of the MF, composing some figures

characterized by symmetry characteristics, and

individualizing some zones of overlap for the figures

themselves. (Karr, Gentry, 1993).

The output of our fuzzy controller, obtained

through the well-known mechanism of

defuzzification, is a crisp value belonging to the

numerical interval [-1;1]. Then we have introduced

two numerical thresholds, a positive and a negative

one. We have made this in order to identify, in

connection with the output value, the corresponding

operative signal (BUY, WAIT and SELL). So we

have made a selection among all the available output

values, choosing just the meaningful ones. In this

way, all of the output values, superior to the negative

threshold or inferior to the positive threshold,

correspond to a WAIT signal. All the output values

superior (inferior) to the negative (positive)

threshold correspond to a BUY (SELL) signal. We

established the two threshold values through an

optimization made once more using GA.

4.2.1 ADX

This input corresponds to ADX. As this index can

assume values in the range [0 100], the

corresponding fuzzy set is the same range. Three

different membership functions have been associated

to this first input (Figure 3):

 CO: a congestion phase, which is a phase in

which market is not in a downward trend nor in

an upward one;

 CT: a not well defined market phase; in this

case we can’t state if a congestion phase is

developing, or if a downward trend or an

upward one is going to an end or confirming

itself;

 TR: a trend, very strengthened or not. This MF

has a trapezoidal shape and, in Figure 3, it has

been cut out at 70.

Figure 3: Membership Functions of ‘ADX’.

4.2.2 perMT1 And perMT2

In FTS, these two inputs are used to represent the

crossing between MACD curve and its trigger line.

First of all, we have to point out the crossing

between these curves. This crossing can be

represented using two helpful situations: yesterday

(i.e. at the time k-1), the difference between MACD

and trigger line was negative while today (i.e. at the

time k) the same difference is positive (MACD’s

curve crossed trigger line from the bottom upwards,

Figure 4-a); yesterday (i.e. at the time k-1), the

difference between MACD and Trigger Line was

positive while today (i.e. at the time k) the same

difference is negative (MACD’s curve crossed

ICEIS 2007 - International Conference on Enterprise Information Systems

326

Trigger Line from the above downwards, Figure 4-

b);

Figure 4: Crossing between curves.

Therefore, our task is to find a suitable formal

representation of the algebraic signs of these

differences, not of their exact value.

We can define two variables:

MT1 = MACD(k-1) – TR(k-1);

MT2 = MACD(k) – TR(k);

Then, we can define the total gap, in the last twenty-

four hours, between MACD and its trigger line as

MT12 = |MT1| + |MT2|

At this point, we can finally introduce our inputs,

defined as the percentage variations of the two

variables MT1 and MT2 in comparison to the total

variation MT12.

This mathematical model makes us sure that the

two variable fuzzy sets are finite and that they

correspond to the range [-100 100]. Moreover, this

model preserves the right signs of the mathematical

differences we have considered.

Three different MF have been associated to the

variable named perMT1 (Figure 5):

 N: negative differences, regarding yesterday

measures; this MF, in Figure 5, has been cut

out at -60.

 Z: differences that are equal to zero, still

regarding yesterday measures;

 P: positive differences, once more as regards

yesterday measures; this MF, in Figure 5, has

been cut out at 60.

Figure 5: Membership Functions of ‘perMT1’.

We used the same MF to represent perMT2.

4.2.3 ACTION

The output variable, named ACTION, represents the

real operative signal that comes out from the

evaluation of all fuzzy rules made by the fuzzy

controller, on the basis of the received inputs.

According to fuzzy logic principles, the three

different signals we have considered (BUY, SELL

and WAIT) have been represented considering some

possible vague situations. So five different MF have

been associated to our output variable, which can

assume values in the range [-1 1] (Figure 6):

 SELL: sell orders;

 ASELL: sell warnings;

 WAIT: wait signals;

 ABUY: buy warnings;

 BUY : buy orders.

Figure 6: Membership Functions of ‘ACTION’.

As we have already said before, output

defuzzification is followed by selection of the really

meaningful values, through the use of the filter

implemented by the two threshold. The optimal

values obtained applying GA optimization are:

= -0,18 S

= 0,35

4.2.4 Fuzzy Rules

The knowledge base of the inference engine of our

fuzzy controller is made up of 27 rules, each of them

has a weight equal to 1. As regards the left part of

these rules, we have chosen the boolean operator

AND as connective. The result of a compound

expression is obtained applying the minimum

method among all values. Besides, the technique

chosen for output defuzzification is the one based on

the calculation of the centroid of the area obtained.

Below there are some of the rules we have

implemented:

MACD–TR>0

(

)

MACD–TR>0

-1

)

MACD–TR<0

-1

)

MACD–TR<0

(k)

MACD

(a)

(b)

A NEW FUZZY LOGIC CONTROLLER FOR TRADING ON THE STOCK MARKET

327

 IF ADX is TR AND perMT1 is N AND

perMT2 is N THEN ACTION=WAIT;

 IF ADX is TR AND perMT1 is N AND

perMT2 is Z THEN ACTION=ABUY;

 IF ADX is TR AND perMT1 is N AND

perMT2 is P THEN ACTION=BUY;

4.3 System Evaluation

We remember that the considerations made for the

TS are also valid for the FTS. We have ignored once

more the costs of all the transactions made, that is

the costs to open and to close an operation don’t

affect on the whole profit; besides, we haven’t

applied any criterion to effect the exit from the

market. These assumptions are the same for both of

the two systems, therefore the base of comparison is

valid.

Now we can reassume the results obtained

applying the FTS on the whole historical data series.

The use of the system from 03/01/2000 to

07/07/2006 has brought the generation of 36 buy

orders and of the same number of sell orders, with a

net profit of 22894 (unit price). Buy and sell signals

are uniformly distributed within the six years taken

for the simulation and we can’t observe any period

of inactivity of the system. The trend of the fuzzy

system equity line (Figure 7) supports the

acknowledgement that fuzzy rules we have chosen

are consistent with the aim of our research, that is

managing only long positions in bull markets. In

fact, we can notice, in the chart, that the curve is

characterized by growing steps in bull market and

horizontal lines in bearing market.

Figure 7: Equity Line of FTS.

We can notice once more some periods when our

system has to face reductions as regards net profit.

This is due, as for TS, to our choice of maintain our

position (WAIT) even in a phase of plain congestion

(ADX lower than its threshold).

As regards performance indexes used for FTS

evaluation (Table 2), we can notice that:

 the Profit/Loss Index (by far greater than 50)

indicates us that on the whole we had more

profits that losses;

 the Reward/Risk Index extremely near to 100,

allows us to state that the system has made

profits with a very low risk factor;

 very high value of the Buy & Hold Index

means that our system multiplies by four the

profit obtained with a Buy And Hold strategy;

 the Win/Lose Index almost equal to 3 means

that the system has made a number of winning

deals greater than the number of losing ones.

Table 2: Performance Indexes.

Profit/Loss Index 73.87

Reward/Risk Index 96.23

Buy & Hold Index 324.04

Win/Lose Index 2.27

5 TS VS FTS

In this section we perform a comparative analysis of

the two different implementations of a trading

system.

The FTS indicates 36 buy signals, and the same

numbers of sell signals which are fewer than those

produced by TS. In both cases, buy signals (sell

signals) are very near to the points in which an

upwards (downwards) trend is growing. The FTS

shows a better attitude than the TS to take

advantages of upwards trends and to point out, at the

right time, the downwards trends. This is due to the

application of fuzzy logic, which allows to decrease

the inaccuracy belonging to technical analysis and to

its instruments that we have applied in our research.

The reduced number of operations suggested by FTS

confirms its attitude to avoid wrong signals. As a

matter of fact, fuzzy logic recognizes, better than the

TS does, the market phase (initial filter). Fuzzy logic

helps the trader avoid some dangerous operations

which must be corrected by additional operations.

For this reason the TS produces a considerable

number of operations but a low profit. Moreover

FTS, compared to TS, is able to contain better the

amount of losses. This means that FTS can reach a

much more higher profit than TS. This profit

remains on very high levels during the whole

simulation. These last considerations are well

evident in the chart (Figure 8) where we have quoted

together the equity lines of the two systems:

ICEIS 2007 - International Conference on Enterprise Information Systems

328

Figure 8: Equity line of FTS and TS.

As far as the performance indexes are concerned,

a quick comparison is enough to state that FTS is

better than the TS, from every point of view. In fact,

the FTS is stronger (it has a better Win/Lose Index

and a better Buy & Hold Index) and it is also much

more reliable (it has a better Profit/Loss Index and a

better Reward/Risk Index) than the TS.

6 CONCLUSIONS

Designing both the non-fuzzy trading system and the

fuzzy one haven’t any pretension to satisfy real

operative aims. The task of our research has been to

show that we’ve been able to improve results of

some simple and well-known rules of technical

analysis through the application of fuzzy logic

principles.

First, we have observed that an automatic

decisional system, planned as an application for

stock market, has to provide a general model which

we have modified and optimized using our own

knowledge: fuzzy logic, a well known technique of

soft computing. As matter of fact, the “transparent”

structure belonging to a fuzzy logic system allows

easy interactions with the trader, through an

interactive employment, but designing a fuzzy

trading system implies some real difficulties to

choose the right parameters for the fuzzy logic

controller. We have solved this problem using

Genetic Algorithms as an optimization technique.

So the task of our research has been the

implementation of a fuzzy trading system (FTS) as

an alternative to an equivalent non-fuzzy trading

system (TS).

Our results have made us state that not only

fuzzy logic is a valid alternative to the classical

implementation of a trading system, but from every

points of view, it also improves its performances.

REFERENCES

A. Elder, Trading for a Living - Wiley Finance Editions

(1993)

Malkiel B.G., A Random Walk down Wall Street, Dow

Jones Irwin (1981)

Fama, E. and IC. French, Business Conditions and

Expected Stock Returns, Joumal of Financial

Economics, Vol. 25, 1989, pp. 23-50

Edwards R.D. Magee J., Technical Analysis of Stock

Trends, Magee (1957)

Goldman Sack, The International Economic Analyst,

Vol7, Issue No. 1 1,1992

Schwager J.D., Fundamental Analysis, Wiley (1995)

Hartle T., Average Directional Movement Index (ADX),

Stocks & Commodities Vol.9, 1991

G.J. Deboeck, Trading on the edge - Wiley Finance

Editions (1994)

Rong-Jun Li Zhi-Bin Xiong, Forecasting stock market

with fuzzy neural networks,Machine Learning and

Cybernetics, 2005, pp.3475 - 3479 Vol. 6, August

2005

Hiemstra, Y., A stock market forecasting support system

based on fuzzy logic, System Sciences, 1994. Vol.III,

pp.281 - 287, Jan 1994

Setnes, M. van Drempt, O.J.H., Fuzzy modeling in stock-

market analysis, Computational Intelligence for

Financial Engineering, 1999,pp. 250 - 258, March

1999

H.S. Ng, K.P. Lam, S.S. Lam Incremental genetic fuzzy

expert trading system for derivatives market timing",

Computacional Intelligence for Financial Engineering,

2003, pp. 421-427, March 2003.

H. Dourra, P. Siy Investment using technical analysis and

fuzzy logic, Fuzzy sets and systems, 127 (2002), pp.

221-240.

Yager, R. R. and L. A. Zadeh (eds.), An Introdiiction to

Fuzzv Logic Applications in Intelligent Svstems,

Kluwer Academic Publishers, Dordrecht, 1992

Zadeh, L.A. Fuzzy Sets as a Basis for a Theory of

Possibility Fuzzy Sets and Systems 1, 1978

Zadeh L.A., Fuzzy Sets, Information and Control, Vol.8,

June 1965,pp. 338-353

Mamdani,E.H. and Assilian,S., An experiment in linguistic

synthesis with a fuzzy logic controller, Int. J.Man

Mach. Studies, Vol. 7, No. 1, 1975

King,P.J. and Mamdani,E.H., The Application of Fuzzy

Control System to Industrial Process, Automatica,

Vol.13., 1977

Karr,C.L. and Gentry,E.J. Fuzzy Control of pH Using

Genetic Algorithms, IEEE Trans.on Fuzzy Systems,

Vol.1, Feb.1993

Davis, L., Handbook of Genetic Algorithms. NY:Van

Nostrand Reinhold, 1991

Goldberg, D.E.. Genetic Algorithms in Search,

Optimization and Machine Learning. US:Addison -

Wesley, 1989

A NEW FUZZY LOGIC CONTROLLER FOR TRADING ON THE STOCK MARKET

329