EXPLANATION GENERATION IN

BUSINESS PERFORMANCE MODELS

With a Case Study in Competition Benchmarking

Hennie Daniels

1,2

and Emiel Caron

Center for Economic Research, Tilburg University, P.O. Box 90153, 5000 LE, Tilburg, The Netherlands

Erasmus Research Institute of Management (ERIM), Erasmus University

P.O. Box 90153, 3000 DR, Rotterdam, The Netherlands

Keywords:

Decision Support Systems, Finance, Production Statistics, Artiﬁcial Intelligence, Explanation.

Abstract:

In this paper, we describe an extension of the methodology for explanation generation in ﬁnancial knowledge-

based systems. This offers the possibility to automatically generate diagnostics to support business decision

tasks. The central goal is the identiﬁcation of speciﬁc knowledge structures and reasoning methods required

to construct computerized explanations from ﬁnancial data and models. A multi-step look-ahead algorithm is

proposed that deals with so-called cancelling-out effects. The extended methodology was tested on a case-

study conducted for Statistics Netherlands involving the comparison of ﬁnancial ﬁgures of ﬁrms in the Dutch

retail branch. The analysis is performed with a diagnostic software application which implements our theory

of explanation. Comparison of results of the method described in (Daniels and Feelders, 2001) with the results

of the extended method clearly improves the analyses when cancelling-out effects are present in the data.

1 INTRODUCTION

Competition benchmarking or interﬁrm comparison

(IFC) is deﬁned as the regular measuring and com-

paring of a company’s performance against its com-

petitors, against industry leaders or industry and his-

toric averages. The aim is often to learn how the com-

pany can improve its own performance. By compar-

ing the ﬁnancial variables of a company with those

of other companies, the company can assess its per-

formance against objective standards and see where

the company is strong or weak. Currently, the diag-

nostic process for IFC is mostly carried out manually

by business analysts (a.o. bankers, accountants and

consultants). The analyst has to explore large data

sets in the domain of business and ﬁnance to spot

ﬁrms that expose exceptional behaviour compared to

some norm behaviour. After abnormal behaviour is

detected the analyst wants to ﬁnd the causes, the set of

ﬁnancial variables responsible, that explain the ﬁrm’s

behaviour. Today’s information systems for auto-

mated ﬁnancial diagnosis and interﬁrm comparison

have little explanation or diagnostic capabilities. Such

functionality can be provided by extending these sys-

tems with an explanation formalism, which mimics

the work of human analysts in diagnostic processes.

In this paper the diagnostic process is fully automated

and implemented in a computer program to support

decision-makers.

Diagnosis is generally deﬁned as ﬁnding the best

explanation of observed symptoms of a system under

study. This deﬁnition assumes that we know which

behaviour we may expect from a correctly working

system. Diagnosis of business performance is deﬁned

as explaining the difference between the actual perfor-

mance of a company and its norm performance. The

norm performance or normative model can be derived

from some statistical model or can be expert knowl-

edge from ﬁnancial analysts. Two important consecu-

tive phases in a diagnostic process are problem identi-

ﬁcation (or symptom detection) and explanation gen-

eration (Verkooijen, 1993). When a discrepancy be-

tween actual and norm behaviour is discovered, and

is qualiﬁed as exceptional with respect to some speci-

ﬁed norm, the next step is to explain this discrepancy

using our “understanding” of the system. There are

many contributions on medical diagnosis and diagno-

sis of technical devices, see (Verkooijen, 1993) for

an overview. A limited number of approaches have

been proposed for the automatic generation of expla-

119

Daniels H. and Caron E. (2007).

EXPLANATION GENERATION IN BUSINESS PERFORMANCE MODELS - With a Case Study in Competition Benchmarking.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 119-128

DOI: 10.5220/0002346101190128

 SciTePress

nations based on ﬁnancial models (Courtney et al.,

1987; Daniels and Feelders, 2001; Feelders, 1993;

Kosy and Wise, 1984).

The rationale behind this paper is to extend the

methodology for automated business diagnosis as de-

scribed in (Daniels and Feelders, 2001; Feelders,

1993). Firstly, a method for symptom detection is pre-

sented that takes into account the probability distribu-

tion of the variable under consideration for diagnosis.

The detection of symptoms for computerized diagno-

sis in ﬁnancial data is not fully developed in earlier

methods, where it is described as the process of tak-

ing the difference value between the actual and norm

value of each variable. Secondly, in this paper we ex-

tend their explanation methodology, with a procedure

to deal with so-called cancelling-out or neutralisation

effects in data sets. For example, the ﬁrst half-year

positive ﬁnancial results could partially cancel out the

negative ﬁnancial results of the next half-year in a ﬁ-

nancial model. If one starts diagnosis with the method

described by Daniels and Feelders on the aggregated

year level these effects are not identiﬁed. However,

these effects are quite common in ﬁnancial data and

other economic data sets and could lead to results in

the form incomplete explanation trees.

This paper is organised as follows. In the next

section we ﬁrst review the explanation model as de-

scribed in literature and introduce extensions for it. In

section 3 the extensions are illustrated by an extensive

case study on interﬁrm comparison with ﬁnancial data

collected at Statistics Netherlands. In the case study

we compare two explanations, in the form of trees of

causes, for detected symptoms derived from compa-

nies in the Dutch retail industry. We compare the trees

generated with and without the look-ahead facility. In

section 4 we brieﬂy describe the software implemen-

tation of the diagnostic program. Finally, we draw a

number of conclusions in section 5. In the appendix

the list of variables and data for interﬁrm comparison

used in the case study are included.

2 METHODOLOGY

Our exposition on diagnostic reasoning and causal

explanation is largely based on the notion of

explanations described in (Daniels and Feelders,

2001; Feelders, 1993), which is essentially based

on Humphreys’ notion of aleatory explanations

(Humphreys, 1989) and the theory of explaining dif-

ferences by Hesslow (Hesslow, 1983). Causal in-

ﬂuences can appear in two forms: contributing and

counteracting. The canonical format for causal ex-

planations is:

ha,F, ribecause C

, despite C

−

where ha,F, ri is the event to be explained, C

is non-

empty set of contributing causes, and C

−

a (possibly

empty) set of counteracting causes. The explanation

itself consists of the causes to which C

jointly refers.

−

is not part of the explanation, but gives a clearer

notion of how the members of C

actually brought

about the symptom. In words, the explanandum is

a three-place relation between an object a (e.g. the

ABC-company) that shows the actual behaviour of a

company, a property F (e.g. having a low proﬁtabil-

ity) that shows the deviation for a particular variable

from its norm value and a reference class r (e.g. other

companies in the same branch or industry) that shows

the norm behaviour. The task is not to explain why a

has property F, but rather to explain why a has prop-

erty F when the other members of r do not. This gen-

eral formalism for explanation constitutes the basis

of our extended framework for diagnosis in ﬁnancial

models developed in this paper.

Two principal knowledge structures for diagnosis

of business performance are identiﬁed:

• Knowledge of general laws, relating variables per-

taining to business performance: the business

model;

• Knowledge of normal behaviour: the normative

model.

In this section we present a summary and propose

some extensions on the general theory and method-

ology for automated business diagnosis.

2.1 The Business Model

Explanations are usually based on general laws ex-

pressing relations between events: such as cause-

effect relations or constraints between variables. The

general laws on which explanations are based, are

represented in the business model M. The business

model M represents quantitative ﬁnancial and operat-

ing variables by means of mathematical equations of

the form:

y = f (x) where x = (x

,...,x

The business model is used to propagate both devi-

ating and non-deviating values. In section 3, an ex-

ample is given of a business model used by Statistics

Netherlands for gathering production statistics in the

retail branch.

A directed graph, the explanatory graph E(M) =

(V , E ), is associated with the business model M. The

vertex set V contains as elements all variables appear-

ing in the model. The edge set E contains a directed

ICEIS 2007 - International Conference on Enterprise Information Systems

120

edge from vertex x

to x

iff: x

= f (...,x

,...) ∈ M.

A restriction is placed on the model M to exclude cy-

cles in the explanatory graph E(M). The arcs between

the nodes in the graph, which represent the variables

in the business model, indicate the direction of inﬂu-

ence, or causal direction. Interpreting the = in the

equations of model M as a ← gives the causal direc-

tion as used by economists, accountants or ﬁnancial

analysts. Thus, in the model the effects appear on the

left-hand side (LHS) of the equations and the causes

on the right-hand side (RHS). However, as we shall

see, the diagnostic reasoning direction is the reverse

of the causal direction. In other words, the explana-

tion generation process takes part from the whole (the

LHS variables) to the parts (the RHS variables).

2.2 The Normative Model

Information seeking or gathering for decision recog-

nition and diagnosis involves both a search for symp-

toms and a search for causes. Pounds (Pounds, 1969)

found that the need for a decision is identiﬁed as a

perceived difference between the actual situation and

some normative model, the expected standard. This

model could be based on either trends past or pro-

jected, comparable situations inside or outside the or-

ganization, expectations of other people or on theo-

retical models. With the exception of crisis, these dif-

ferences normally do not present themselves readily

to the decision maker but must be ﬁltered from the

constant streams of ambiguous data received. The

normative model speciﬁes which reference object(s)

should be used to compare. It also speciﬁes the vari-

ables with respect to which the comparison should be

made. The most common “reference objects” to di-

agnose business performance are: historical reference

values, industry averages and plans and budgets.

2.3 Symptom Detection

Diagnosis in a ﬁnancial model is the explanation for

observed exceptional behaviour of a company. The

ﬁrst step in diagnostic process is problem or symptom

identiﬁcation, the detection of abnormal behaviour.

The central question in problem identiﬁcation for

business diagnosis is: “Which ﬁrms deviate signif-

icantly from their branch average or historic aver-

age?” Suppose the normative model contains a ref-

erence value for variable y. The data set may con-

tain several reference values, besides the actual val-

ues for business variables. For diagnosis of company

performance the event to be explained with actual

object a and reference object r will always be clear

from the context, therefore the explanation formal-

ism is simpliﬁed to: ∂y = q occurred because C

, de-

spite C

−

. In this expression, ∂y = y

− y

= q where

q ∈ {low,normal,high}, speciﬁes an event in the ﬁ-

nancial data set, i.e. the occurrence of a quantitative

difference between the actual and the reference value

of y, denoted by y

and y

, respectively. Note that for

the purpose of diagnosis, it is not interesting to ex-

plain symptoms with the label ∂y = “normal”, since

it is only required to explain why a variable deviates

from its reference value.

Problem identiﬁcation is a process where a value

g(y

) is computed for each variable, where g is

some user-deﬁned function such as percentage or ab-

solute difference. Here a method is developed that

can take into account the probability distribution, e.g.

the normal distribution, of the business variable un-

der consideration. In this method ﬁrst the average

value for each variable is estimated based on a sta-

tistical model. When a statistical model is used as a

normative model then y

= ˆy. If we now normalize

the residual of the model by the standard deviation σ

of the variable in the sample, we get the normalized

residual ∂y/σ. The exact population parameters of the

distribution are usually unknown; therefore they are

estimated and replaced by the sample mean and sam-

ple variance. Correspondingly, the problem of look-

ing for exceptional company behaviour is equivalent

to the problem of looking for exceptional normalized

residuals. Statistically deﬁned, a variable is a symp-

tom or exceptional value if it is higher (lower) than

some user-deﬁned threshold δ (−δ). Usually, we se-

lect δ = 1.645 corresponding to a probability of 95%

in the standard normal distribution. Automatically,

the following series of statistic tests is performed on

each variable in the business model to detect symp-

toms in the data set under consideration:

• if ∂y/s > δ (one-tailed test) then the symptom is

labelled ∂y = “high”,

• if ∂y/s < −δ (one-tailed test) then the symptom is

labelled ∂y = “low” and

• if −δ ≤ ∂y/s ≤ δ then the symptom is labelled

∂y = “normal”.

2.4 Diagnosis and Explanation

If ∂y = q is identiﬁed as a symptom, we want to

explain the difference ∂y = y

− y

. An explana-

tion is based on the ﬁnancial equations of the busi-

ness model. To determine the contributing and coun-

teracting causes that explain the quantitative differ-

ence between the actual and reference value of y, a

measure of inﬂuence is deﬁned in literature (Daniels

and Feelders, 2001; Feelders, 1993; Kosy and Wise,

EXPLANATION GENERATION IN BUSINESS PERFORMANCE MODELS - With a Case Study in Competition

Benchmarking

121

1984) as follows:

inf(x

,y) = f (x

−i

) − y

where f (x

−i

) denotes the value of f (x) with

all variables evaluated at their reference values,

except x

. In words, inf(x

,y) indicates what the

difference between the actual and reference value of

y would have been if only x

would have deviated

from its reference value. Here it is assumed that

= f (x

,...,x

) and y

= f (x

,...,x

). Fur-

thermore, the function f has to satisfy the so-called

conjunctiveness constraint (Daniels and Feelders,

2001; Feelders, 1993). This constraint captures the

intuitive notion that the inﬂuence of a single variable

should not turn around when it is considered in

conjunction with the inﬂuence of other variables.

Two classes of functions satisfy the conjunctiveness

constraint, namely additive and monotonic functions,

that frequently occur in business model relations.

By monotonicity we mean the monotonicity in all

variables separately, on the domain under considera-

tion. The form of the reference function depends on

the type of statistical model applied. In the situation

that actual and reference function are both additive,

then inf(x

,y) is correctly interpreted as a quantitative

speciﬁcation of the change in y that is explained by a

change in x

If f =

∑

k=1

) (actual function is additive; s

’s are

arbitrary functions) and y

∑

k=1

) then

∂y = y

− y

∑

i=1

inf(x

,y)

− y

∑

k=1

)−

∑

k=1

)

inf(x

,y) =

∑

k6=i

) + s

) − y

= s

) − s

)

and therefore:

∑

i=1

inf(x

,y) = y

− y

Furthermore, if f is non-additive but differen-

tiable, y

= f (x

) and δ

= x

− x

is small then ∂y ≈

∑

i=1

inf(x

,y). However, in general ∂y is not neces-

sarily equal to ∂y =

∑

i=1

inf(x

,y). This occurs when

6= f (x

), or when f is non-additive and δ

= x

−x

is large. For monotonic functions, the interpreta-

tion of inf(x

,y) becomes more difﬁcult and context-

dependent, but the sign of inf(x

,y) is not context-

dependent. Therefore sometimes reference values are

made internally consistent in this situation to main-

tain the assumption of y

= f (x

The deﬁnition of the inﬂuence-measure makes it

possible to operationalize the concepts of contribut-

ing and counteracting causes. When explanation is

supported by a business model equation, the set of

contributing (counteracting) causes C

−

) consists

of measures x

of x with inf(x

,y) × ∂y > 0 (< 0). In

the explanation method, insigniﬁcant inﬂuences are

left out of the explanation by a ﬁlter measure. The set

of causes is reduced to the so-called parsimonious or

signiﬁcant set of causes. The parsimonious set of con-

tributing causes C

is the smallest subset of the set of

contributing causes such that inf(C

,y)/inf(C

,y) ≥

. The parsimonious set of counteracting causes

is deﬁned analogously. The fraction T

and T

−

are

numbers between 0 and 1, and will typically 0.85 or

so.

Furthermore, in (Daniels and Feelders, 2001;

Feelders, 1993) the concept of the maximal explana-

tion method is deﬁned. The idea is that for ∂y = q, ex-

planation generation is continued (top-down) only for

its parsimonious contributing causes, whereas non-

parsimonious causes and counteracting causes are not

explained any further. This process is continued un-

til a contributing cause is encountered that cannot be

explained within the business model M, because the

business model does not contain a relation in which

this contributing cause appears on the LHS. Max-

imal explanation extends the idea of one-level ex-

planations, that is based on only one relation from

the business model, to multi-level explanations. The

maximal explanation process results in a so-called

tree of causes (or explanation tree), where y is the

root of the tree and its children, grandchildren, great-

grandchildren and so on are parsimonious contribut-

ing and counteracting causes. In this way explana-

tions are chained together and a tree of causes is

formed.

2.5 Making Hidden Causes Visible by

Substitution

The explanation methodology as described in the lit-

erature (Daniels and Feelders, 2001; Feelders, 1993;

Kosy and Wise, 1984) has the shortcoming that it can-

not deal with so-called cancelling-out or neutralisa-

tion effects. Cancelling-out is the phenomenon that

the effects of two or more lower-level variables in

the business model cancel each other out so that their

joint inﬂuence on a higher-level variable in the busi-

ness model is partly or fully neutralized. These ef-

fects are quite common in ﬁnancial models as we

shall see in the case study. For the top-down explana-

tion generation process this means that in some data

sets possible signiﬁcant causes for a symptom will not

be detected when cancelling-out effects are present.

These non-detected causes by multi-level explanation

are called hidden causes. Hidden causes are signif-

icant causes that are not visible at ﬁrst due to the

ICEIS 2007 - International Conference on Enterprise Information Systems

122

neutralisation of a higher level variable in the busi-

ness model. In theory, cancelling-out effects may oc-

cur at every level in the business model. Therefore,

one does not have a clue a priori on what level in the

business model detection for these effects should start

and whether these effects are signiﬁcant or not. Of

course, ﬁnancial analysts would like to be informed

about signiﬁcant hidden causes, and would consider

an explanation tree without mentioning these causes

as incomplete and not accurate.

Suppose that we are explaining a symptom ∂y = q

with the following equations out of business model M

y = f (x) ∈ M

0;1

, (1)

= g

(z) ∈ M

1;2

. (2)

Where x = (x

,...,x

,...x

) and z = (z

,...,z

) de-

note n and m-component vectors. The depth of the

business model (N) is deﬁned as the number of lev-

els in M or associated directed graph. The root of the

tree (y) is on level 0, the children of the root (vari-

ables x

,...,x

) are on level 1, the grandchildren

of the root are on level 2, and so on. Furthermore,

LHS(l

);RHS(l

)

represents the set of equations with

the LHS on level l

and the RHS on level l

of M. We

write M

p;q

for short, where p = 0,1,...,N − 1 and

q = p + 1. The root equation is represented by M

0;1

the equations for its children are represented by M

1;2

the equations for its grandchildren are represented by

2;3

, and so on. Furthermore, suppose that expla-

nation generation with eq. 1 results in sets of parsi-

monious causes where variable x

is not part of, thus

/∈ C

(y) and x

/∈ C

−

(y). In words, the variable

is not signiﬁcant because it has a marginal inﬂu-

ence on the root y. An extreme situation occurs when

inf(x

,y) = 0, then the variable x

has no inﬂuence on

∂y. To make sure that the explanation is complete all

successors of x

have to be investigated for possible

cancelling-out effects. Therefore, all children of x

(the elements of z) are substituted into the RHS of eq.

1 to derive the substituted function

y = h

(x,z) ∈ M

0;2

. (3)

The result of substituting jointly all equations at level

q;q+1

in the business model into a parent equation

p;q

is denoted by M

p;q+1

, this is called one-step

look-ahead. Subsequently, the substituted equation is

added to the business model M and considered for ex-

planation generation.

Deﬁnition 1. Variable z

of eq. (3) is a hidden cause

when z

∈ C

(y) under the condition that x

/∈ C

(y).

In words, variable z

of eq. (3) (the result of substi-

tuting eq. (2) into eq. (1)) is a hidden cause when

its inﬂuence on y – its grandparent – is signiﬁcant in

explanation generation, under the condition that the

inﬂuence of variable x

– its parent – of eq. (1) on y is

not signiﬁcant. Here the inﬂuence of z

on y is given

by: inf(z

,y) =

f (x

,...,g

,...,z

),...,x

)−

f (x

,...,g

,...,z

),...,x

and the inﬂuence of x

on y is given by: inf(x

,y) =

f (x

,...,x

) − f (x

,...,x

) =

f (x

,...,g

),...,x

) − f (x

,...,g

),...,x

This means that the effect of z

is neutralized by the

effects of other variables in the vector z. Moreover,

it is assumed that the derived function h

satisﬁes the

conjunctiveness constraint. In the special case that the

functions f and g

from eq. (1) and (2) are both ad-

ditive the following holds: inf(x

,y) =

∑

j=1

inf(z

,y).

From this relation it immediately follows that when

/∈ C

(y) and z

∈ C

(y) at least one variable out of

z is in the set of counteracting causes C

−

(y). Or vice

versa, when x

/∈ C

(y) and z

∈ C

−

(y) at least one

variable out of z is in the set of contributing causes

(y).

In addition, one-step look-ahead can simply be ex-

tended to multi-step look-ahead. For example, two-

step look-head is deﬁned as one-step look-ahead plus

p;q+2

, the result of substituting all equations at level

q+1;q+2

into M

p;q+1

, three-step look-head is deﬁned

as two-step look-ahead plus M

p;q+3

, the result of sub-

stituting all equations at level M

q+2;q+3

into M

p;q+2

and so on. In general, for a business model with depth

N, the maximal number of look-ahead steps is N − 1.

In multi-step look-ahead, a successor of variable x

a hidden cause if its inﬂuence on y is signiﬁcant af-

ter substitution, when the inﬂuence of variable x

eq. (1) on y is not signiﬁcant. Basically, the multi-

step look-ahead method is an extension of the maxi-

mal explanation method (Daniels and Feelders, 2001;

Feelders, 1993). In short, the look-ahead method is

composed of two consecutive phases: an analysis (1)

and a reporting phase (2). In the analysis phase the

explanation generation process starts, similar as for

maximal explanation, with the root equation in the

business model by determining parsimonious causes.

However, instead of proceeding with strictly parsi-

monious causes, all non-parsimonious contributing

and counteracting causes are investigated for possi-

ble cancelling-out effects at a speciﬁc level in M. In

this phase hidden causes are made visible by means of

function substitution, where all the lower-level equa-

tions at level j in the business model are substituted

into the higher-level equation under consideration for

explanation. In addition, the substituted functions are

added to M and considered for explanation genera-

tion. In the reporting phase the explanation tree is up-

dated when hidden causes are detected by the multi-

EXPLANATION GENERATION IN BUSINESS PERFORMANCE MODELS - With a Case Study in Competition

Benchmarking

123

level look-ahead method. As in maximal explanation

causes are presented to the analyst in the form of a

tree of causes. In fact, the explanation tree gener-

ated with maximal explanation needs to be updated

when signiﬁcant hidden causes are present in the sub-

stituted equations. In updating the tree new parsimo-

nious causes are added and causes that have become

non-parsimonious are removed.

The look-ahead functionality, when activated, is

applied as an extension of maximal explanation and

executed each time after parsimonious causes have

been determined with one-level explanation. When

the multi-step look-ahead algorithm is conﬁgured

with p = 0 (explanation starts with the root equa-

tion) and maximal number of look-ahead steps (N −1)

then all signiﬁcant (hidden and non-hidden) causes

are made visible by substitution and maximal expla-

nation is only used for initialization. The number of

look-ahead steps (the horizon) in the business model

is user-deﬁned and based on the domain knowledge of

the analyst. The pseudo code of the multi-step look-

ahead algorithm is given in the Appendix.

3 INTERFIRM ANALYSIS AT

STATISTICS NETHERLANDS

The business model and data for IFC in this case

study are obtained from Statistics Netherlands

(Statistics Netherlands, 2006). Statistics Netherlands

is responsible for collecting, processing, and pub-

lishing statistics used in practice, by policymakers

and for scientiﬁc research. The business model

M we present is based on the survey structure for

gathering production statistics from companies in the

Dutch retail and wholesale trade. In addition, we

use production statistics from two consecutive years,

the year 2001 and 2002. For both years, data sets

with more than 5000 different retail and wholesale

companies are classiﬁed into branch sections. The

following business model relations and ﬁnancial

model variables are used

1. r

= r

+ r

2. r

= r

− r

3. r

= r

− r

4. r

= r

− r

5. r

= r

− r

6. r

= r

+ r

7. r

= r

+ r

8. r

= r

+ r

9. r

= r

+ r

19. r

= r

+ r

In short, three types of business equations are

identiﬁed in M (with depth N = 4): result (eq. 1

through 5), revenue (eq. 6 through 8), and cost (eq. 9

through 19) equations. The variable (r

) in the root

result equation gives the company’s total result before

taxation. This variable is split up into four types

of results namely: total operating results (r

), total

ﬁnancial results (r

), total results allowances (r

and total extraordinary results (r

). In the Appendix

the descriptions of the other variables in M are given.

Several factors that may have an inﬂuence on the

business diagnosis results have to be taken into ac-

count, like the Standard Industry Classiﬁcation (SIC)

for the retail and wholesale industry and the size

of the company. Therefore, computerized selections

on the data set are made, like: supermarkets, liquor

stores, do-it-yourself shops, etc. Within these subsets

we make a further selection on the size class (small,

medium and large) of the companies. The company

size classes are based on the number of employees

of the ﬁrm in FTE’s (full-time employees) and the

intervals for the different size classes are: small (1

through 9 employees), medium (10 through 99 em-

ployees) and large (from 100 employees and more).

In this way homogeneous subsets of the data for anal-

ysis are constructed. In addition, we normalised the

data by dividing all variables in M by the total num-

ber of FTE’s of each individual company. Reference

objects. The reference object for IFC, the industry av-

erage, is computed by taking the mean value of all the

companies in the selected normalized sample of a spe-

ciﬁc year for all variables (r

through r

) in the busi-

ness model. Moreover, for historic comparisons the

reference objects for the business model variables are

the values in one or more previous time periods, for

example, we can benchmark the results for the current

year with the results of the previous year for a certain

company.

3.1 Symptom Detection

Analysis is performed on a speciﬁc homogeneous

sample selected out of the original data set with pro-

duction statistics for the year 2001. The selected sam-

ple is composed out of 69 fashion shops out of the size

class “medium”. Problem identiﬁcation in the data set

starts with the variable results for taxation (r

) on the

root level of the business model. This variable has

a normal distribution (tested with the Shapiro-Wilks

normality test) with mean 11.30 (the industry aver-

age) and standard deviation 28.85. The exact pop-

ICEIS 2007 - International Conference on Enterprise Information Systems

124

ulation parameters of the distribution are unknown;

therefore they are estimated and replaced by the sam-

ple mean and sample variance. The central question in

problem identiﬁcation for this case study is: “Which

ﬁrms deviate signiﬁcantly from their branch average

in 2001?” The symptom detection module of the di-

agnosis application identiﬁes 9 ﬁrms that are higher

(or lower) than the speciﬁed threshold value in the

sample data set (see Table 1 for a full speciﬁcation

of the norm model). Here we select δ = 1.645 corre-

sponding to a probability of 95% in the standard nor-

mal distribution. With these test speciﬁcations we de-

rive the following distribution of the number of ﬁrms

over the three symptom types: 5 ﬁrms with symptom

high, 60 ﬁrms with symptom normal and 4 ﬁrms with

symptom low.

Table 1: Speciﬁcation of normative model for example.

slot name slot entry

variable results before taxation (r

)

norm object industry average (2001)

industry fashion shops

size class (69 ﬁrms) medium

distribution r

∼ N(11.30, 832.17)

threshold α = .05 (two one-tailed tests)

For one of the fashion shops in the sample –

the ABC-company – we present complete diagnos-

tics. Moreover, the data is anonimized because Statis-

tics Netherlands does not allow exposure of data

on the micro level. For the ABC-company the de-

tected symptom is “high” when comparing the ac-

tual result before taxation of the company with the

branch average, because the one-tailed test (61.75 −

11.30)/28.85 > 1.645 is above the threshold value.

Furthermore, the relative difference between the ac-

tual value and industry average for r

is (61.75 −

11.30)/11.30 = 4.46. Thus, the ABC-company is do-

ing particularly good compared to its industry aver-

age, more than 4 times as good.

3.2 Example Explanation Generation

In this section a comparison is made between

the results of two explanations for the symptom:

hABC-company(2001), ∂r

= high, branch average

(2001)i. We will address the following question:

“Why are results before tax (r

) relatively high for the

ABC-company compared with its branch average?”

The explanation for this event is generated by maxi-

mal explanation method. However this method will

not give the complete explanation in the case of

cancelling-out effects. Moreover, a comparison be-

tween human analysis and the classic explanation

method shows noticeable differences when these ef-

fects occur. Therefore, we present a second expla-

nation generated with detection for hidden causes

switched on. The two explanations and additional

explanation trees are both generated automatically by

our prototype computer program.

3.2.1 Maximal Explanation Generation

The maximal explanation without look-ahead yields

the following results, taking for the fraction T

−

= 0.85. In Table 2 a comparison is made be-

tween the actual results before taxation of the ABC-

company and the branch average in the year 2001.

From the data in the table we infer that C

= {r

}

and C

−

0. The variable r

(total operating results)

explains 90.44% of the difference ∂r

, and is there-

fore identiﬁed as the single parsimonious contributing

cause because its value exceeds the fraction. Thus, the

result variables r

, r

and r

are ﬁltered out of the ex-

planation because their inﬂuences are considered to

be too small. Therefore, the variable r

is the single

child node of its parent (root node) r

in the explana-

tion tree.

Table 2: Actual and norm values for r

= r

+ r

actual norm inf(x

,y) diff. %

61.75 11.30 446.46

60.42 14.79 45.62 308.52

1.33 -2.55 3.88 -152.16

0.00 -0.15 0.15 -100.00

0.00 -0.79 0.79 -100.00

The diagnostic process is continued only for

this parsimonious contributing cause. Further ex-

planation is generated by equation 2 of M, to

explain the initial difference in ∂r

. Explana-

tion generation with the multi-step look-ahead algo-

rithm shows that cancelling-out effects are present

in this example. And hidden causes that stan-

dard are left undetected by maximal explanation

are found in the look-ahead procedure. The next

event (analogous to the previous example) to be ex-

plained is speciﬁed as: hABC-company(2001), ∂r

high, branch average(2001)i. Table 3 summarizes

the results for the explanation of the ABC-company’s

relative high total operating result. From the data

in the table it follows that C

= {r

}, since both

(explains 45.73%) and r

(explains 54.73%) con-

tributed to the difference between norm value and the

actual value, and are both needed to explain the de-

sired fraction of inf(C

). In words, the total op-

erating results for the ABC-company are relatively

high, because of the fact that the total operating rev-

EXPLANATION GENERATION IN BUSINESS PERFORMANCE MODELS - With a Case Study in Competition

Benchmarking

125

enues (r

) are high and the total operating costs (r

)

are low in comparison with their branch averages.

Obviously, C

−

0. Thus, the variable r

has two chil-

dren in the explanation tree. Both children correspond

to equations (eq. 6 and 9) in the business model and

can therefore be explained further.

Table 3: Actual and norm values for r

= r

− r

actual norm inf(x

,y) diff. %

60.42 14.79 308.52

329.50 308.64 20.86 6.76

269.09 293.84 24.76 -8.42

Analogous to the previous example, the

new events to be explained are speciﬁed as:

hABC-company(2001), ∂r

= high, branch average

(2001)i and hABC-company(2001), ∂r

= low,

branch average(2001)i. In other words, we want

to determine which lower level revenues and costs

variables in the business model contributed sig-

niﬁcantly to these events. For these equations the

inﬂuence values are omitted because of space limita-

tions. The previous examples of different one-level

explanations are now combined to a complete tree

of causes. Fig. 1 summarizes the results of the

complete diagnostic process, where dashed lines

indicate counteracting causes. Since there is only one

symptom to be explained, the diagnosis contains one

maximal explanation. Thus, Fig. 1 actually depicts

the maximal explanation, as speciﬁed in section 2.4,

for ∂r

= “high”.

Figure 1: Diagnosis for S = {∂r

= high} at ABC-company.

3.2.2 Explanation Generation with Multi-step

Look-ahead

In this section, we explain the initial event for the

ABC-company with the look-ahead method. The

method in the diagnostic program is conﬁgured for

one-step look-ahead. For the threshold value we take

again T

= T

−

= 0.85. As before, explanation gen-

eration starts again with the root equation. From the

data in Table 2 the same set of causes as with max-

imal explanation is identiﬁed. However, instead of

proceeding with purely explanation of the parsimo-

nious contributing causes the methods looks for po-

tential cancelling-out effects, one step ahead in the

business model. The look-ahead procedure takes into

account the effects of all variables one level deep, i.e.

the effects of the RHS-variables in equations 2, 3, 4

and 5.

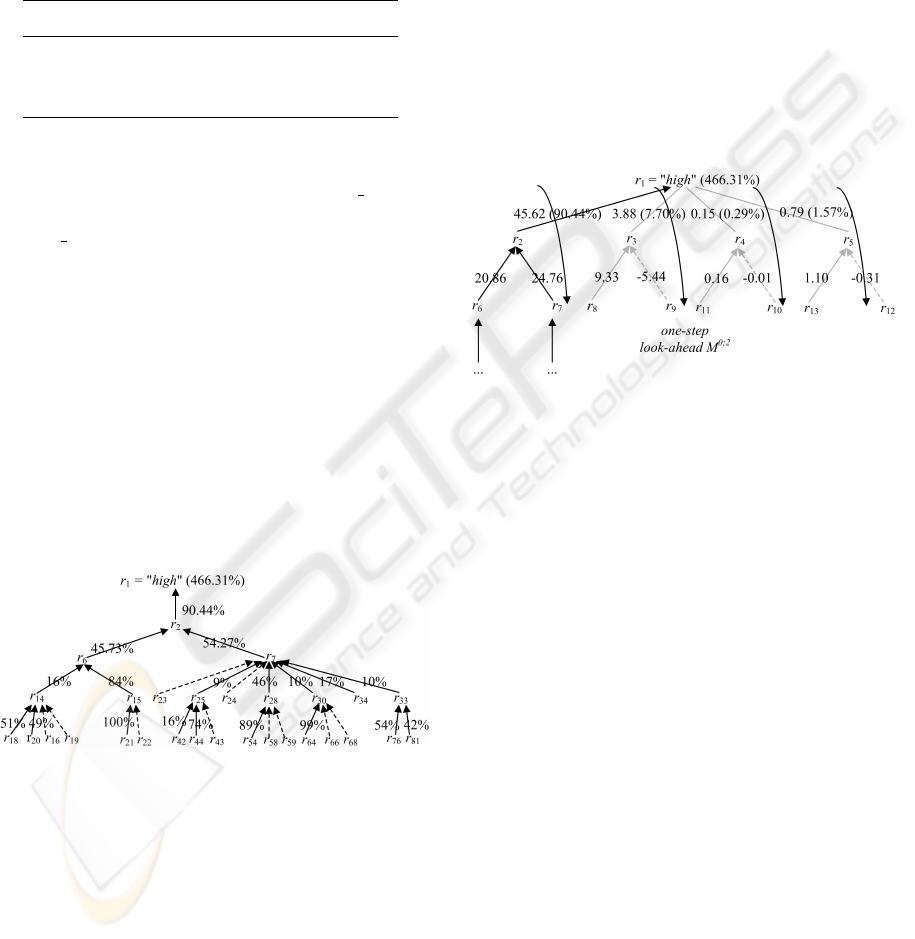
Fig. 2 shows the one step look-ahead with arrows

“stepping over” the intermediate nodes, and pointing

at the RHS variables of equation 2, 3, 4 and 5, in

the partial explanation tree. In this ﬁgure, the straight

black lines indicate the parsimonious causes that were

detected with maximal explanation.

Figure 2: Illustration of one-step look-ahead.

In the analysis phase of the procedure the function

substitution is applied to ﬁnd parsimonious contribut-

ing and counteracting causes, which were missed

in the local explanation of differences by standard

multi-level explanation. Equations 2 through 5 are

substituted into the root equation and the follow-

ing new equation for explanation generation is de-

rived: M

0;2

: r

= (r

− r

) + (r

− r

) + (r

− r

) +

− r

). This equation obtained by substitution is

added to the set of business model equations, chang-

ing the original business model. Because the substi-

tuted function is again additive, the conjunctiveness

constraint is satisﬁed. Notice that the speciﬁcation of

the event to explain ∂r

remains the same, but now

equation M

0;2

is applied to explain the difference. Ta-

ble 4 summarizes the results of our extended model

of ABC-company’s relatively high results before tax-

ation. It follows that C

= {r

} and C

−

= {r

We conclude that the effects of causes r

and r

are

signiﬁcant at the speciﬁed fractions for parsimonious

sets.

Notice that these hidden causes were missing in

analysis with maximal explanation. For the tree of

causes this means that two new children are added to

the root node: a contributing child for r

and a coun-

teracting child for r

. As a result the top branches of

ICEIS 2007 - International Conference on Enterprise Information Systems

126

Table 4: Actual and norm values for M

0;2

: r

= (r

− r

) +

− r

) + (r

− r

) + (r

− r

actual norm inf(x

,y) diff. %

61.75 11.30 466.31

329.50 308.64 20.86 6.76

269.09 293.84 24.76 -8.42

11.17 1.84 9.33 507.07

9.83 4.39 -5.44 123.92

0.00 0.16 0.16 -100.00

0.00 0.01 -0.01 -100.00

0.00 0.31 -0.31 -100.00

0.00 1.10 1.10 -100.00

the original tree are updated, as can be seen in Fig.

3. Notice that the variable r

is not part of the tree of

causes (grey line).

Figure 3: Detection of hidden causes with M

0;2

of S =

{∂r

= high}.

4 IMPLEMENTATION

In this section we shortly present the software imple-

mentation of the prototype diagnosis application in

MS Excel in combination with Visual Basic. This ap-

plication is initially programmed to perform the ex-

periments and analyses for the case study at Statis-

tics Netherlands. However the prototype software can

handle data and business models from multiple appli-

cation domains. Most elements of the program are

discussed in the previous parts of this paper. How-

ever the procedure diagnostic component was not dis-

cussed earlier. It contains the method for maximal

explanation as well as the multi-step look-ahead al-

gorithm. For the implementation of the procedure

we applied tree programming to generate the tree of

causes.

Figure 4: Tree viewer in diagnosis application.

The tree-viewer interface of the program is de-

picted in Fig. 4. In the viewer the whole explanatory

graph can be made visible my manipulating the tree.

In addition, the tree of causes is projected on the ex-

planatory graph by highlighting parsimonious causes

with a colour. By clicking on the cause under consid-

eration the details for the cause become visible in the

right panel of the screen.

5 SUMMARY AND CONCLUSION

In this paper, we extended the method for automated

business diagnosis in (Daniels and Feelders, 2001;

Feelders, 1993) and developed a new implementation.

The explanation model is extended in two ways: in

the symptom detection phase the probability distri-

bution of business model variables is taken into ac-

count and in the explanation generation phase hidden

causes can be made visible by function substitution.

The problem of looking for exceptional company be-

haviour in ﬁnancial data sets is translated into the

problem of looking for exceptional normalized resid-

uals. Furthermore, the multi-level look-ahead algo-

rithm is proposed to enhance the explanation method-

ology so that it can deal with cancelling-out effects,

i.e. the common effect that variables cancel each

other out somewhere in the business model with the

result that their effect on a higher level in the business

model is partially or fully neutralized. The extended

model is implemented in VB. Within the software im-

plementation special attention is given to presentation

of the program output, where symptoms and causes

are presented graphically as a tree of causes. In this

manner, a manager or ﬁnancial analyst can view and

access the results of the explanation process for diag-

EXPLANATION GENERATION IN BUSINESS PERFORMANCE MODELS - With a Case Study in Competition

Benchmarking

127

nosis of company performance as a compact tree.

The applicability of the method is illustrated in

a case study on interﬁrm/historic comparison in the

Dutch retail and wholesale trade, based on produc-

tion statistics obtained from Statistics Netherlands.

In the case study it is shown that in the presence of

cancelling-out effects the extended model with the

multi-level look-ahead procedure makes signiﬁcant

causes visible that would be missed by the explana-

tion methodology of maximal explanation. In addi-

tion, the fully automated diagnostic process makes it

possible to detect and explain abnormal company be-

haviour in large data sets. We believe that this en-

hanced framework could assist analysts and improve

the decision-making process, by automatically gener-

ating explanations for exceptional values in various

data sets and business models.

REFERENCES

Courtney, J. F., Paradice, D. B., and Mohammed, N. H. A.

(1987). A knowledge-based dss for managerial prob-

lem diagnosis. Decision Sciences, 18(3):373–399.

Daniels, H. A. M. and Feelders, A. J. (2001). A general

model for automated business diagno sis. European

Journal of Operational Research, 130:623–637.

Feelders, A. J. (1993). Diagnostic reasoning and expla-

nation in ﬁnancial models of the ﬁrm. PhD thesis,

Tilburg University, Department of Econo mics.

Hesslow, G. (1983). Explaining differences and weighting

causes. Theoria, 49:87–111.

Humphreys, P. W. (1989). The chances of explanation.

Princeton University Press, New Jersey.

Kosy, D. W. and Wise, B. P. (1984). Self-explanatory ﬁ-

nancial planning models. In Proc. of AAAI-84, pages

176–181, Austin, TX.

Pounds, W. F. (1969). The process of problem ﬁnding. In-

dustrial Management Review, 11(1):1–19.

Statistics Netherlands (2006). Centraal bureau voor de

statistiek.

Verkooijen, W. J. (1993). Automated ﬁnancial diagnosis: a

comparison with other diagnostic domains. J. Inf. Sci.,

19(2):125–135.

APPENDIX

Because of space limitations only the description of the

variables identiﬁed by the explanation model are described

here in detail.

Result variables:

: total operating revenues

: total operating costs

: ﬁnancial revenues

: ﬁnancial expenses

: additions to allowances

: deductions from allowances and provisions released

: extraordinary proﬁts

: extraordinary losses

Revenue variables:

: total additional revenues

: total net sales

: net sales other activities

Cost variables:

: cost of goods sold

: total costs of labour

: depreciations on tangible and intangible ﬁxed assets

Algorithm: Multi-level Look-ahead

1: y is the root node of the tree

2: for p = 0 to N − 1 do

3: determine parsimonious causes for equation(s)

p;p+1

4: add parsimonious causes to the tree as successor

nodes

5: if look-ahead is activated then

6: for i = 1 to N − 1 do

7: substitute jointly all equations on M

p+i;p+i+1

into equation M

p;p+i

8: add derived equation M

p;p+i+1

to M

9: determine parsimonious causes for M

p;p+i+1

10: if causes on level p + i + 1 are parsimonious

then

11: add new parsimonious causes as successor

nodes to the tree

12: remove non-parsimonious causes from the

tree

13: if a node corresponds to counteracting cause then

14: it has no successors

15: if a node corresponds to variable that cannot be ex-

plained in M then

16: it has no successors

ICEIS 2007 - International Conference on Enterprise Information Systems

128