ARCHITECTURAL DESIGN VIA DECLARATIVE PROGRAMMING

ıs Moniz Pereira and Ruben Duarte Viegas

Faculdade de Ci

encias e Tecnologia, Universidade Nova de Lisboa, Monte da Caparica, Portugal

Keywords:

Architectural design, declarative design support system, solution generation by constraint solving, logic pro-

gramming for design.

Abstract:

Problem solving by declarative theory building can be an extremely effective method for porting concepts and

knowledge from the problem domain to the solution do main, by allowing the implementation of complete

procedural constructs and enabling to produce sound solutions. If conveniently expressed, such a theory

may be directly coded into a declarative programming language. If expressed within the paradigm of logic

programming, then the theory itself represen ts the very procedure to obtain its desired solutions.

The illustrative case study considered here is the obtention of architectural layouts from an adjacency graph:

Given a list of imposed adjacencies among a set of planar rectangular spaces (represented by the graph’s

nodes), the goal is to generate all permissible layouts schemas on the plane which respect the adjacencies, and

to determine the minimal modular dimensions of such a set of spaces.

Another aim of this article is also to show the guidelines of an effective translation of the theory constructed

to solve the proposed problem in Logic Programming, making use of the combined power of two different

semantics and their implementations, namely the Well Founded Semantics and the Stable Models one.

1 INTRODUCTION

In the architectural domain, the problem of specifying

a set of possible architectural layouts for construction

purposes is of critical importance. The constraints in-

volved in such a speciﬁcation are often complex and

interleaved, involving matters of topology such as the

required or impossible adjacencies in a set of layout

plant spaces and matters of dimension regarding the

size of each space in order to minimize construction

material or to maximize space within the building’s

architectural skeleton. Additional constraints apply

to the overall shape of the layouts’ contours.

The problem considered here approaches these is-

sues and promotes automatic methods for the gener-

ation of valid alternative layouts given such sets of

constraints. In this case, a necessary adjacencies list

is initially given, specifying constraints on the topol-

ogy of the modular layout spaces.

A method of building a requirements theory to

solve the general problem was ﬁrst elaborated and

presented in (Pereira, 1974; Pereira, 1978) and, as

such, the main concern here is to provide an efﬁcient

translation into a logic program of that theory. This

is accomplished in what regards the determination of

the permissible hv-assignments constraints to edges

(i.e. the assignment of the horizontal or vertical la-

bels to each adjacency edge to signal the relative po-

sition of the corresponding separating wall between

its two adjacent spaces; and, also, in what regards the

determination of the minimal compatible modular di-

mensions for each space; and, ﬁnally, in what regards

the drawing of the associated layout scheme).For an

example, see Fig 1 below.

The problem offers today the same challenge it

did three decades ago, when Algol68 language was

the programming vehicle. It is generally highly and

elaborately constrained, with each constraint very dif-

ﬁcult to implement or even approach, since some of

the concepts related to the architectural background

are relatively complex. Furthermore, given the over-

all complexity of the problem, it is quite difﬁcult to

363

Moniz Pereira L. and Duarte Viegas R. (2007).

ARCHITECTURAL DESIGN VIA DECLARATIVE PROGRAMMING.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 363-369

DOI: 10.5220/0002346503630369

 SciTePress

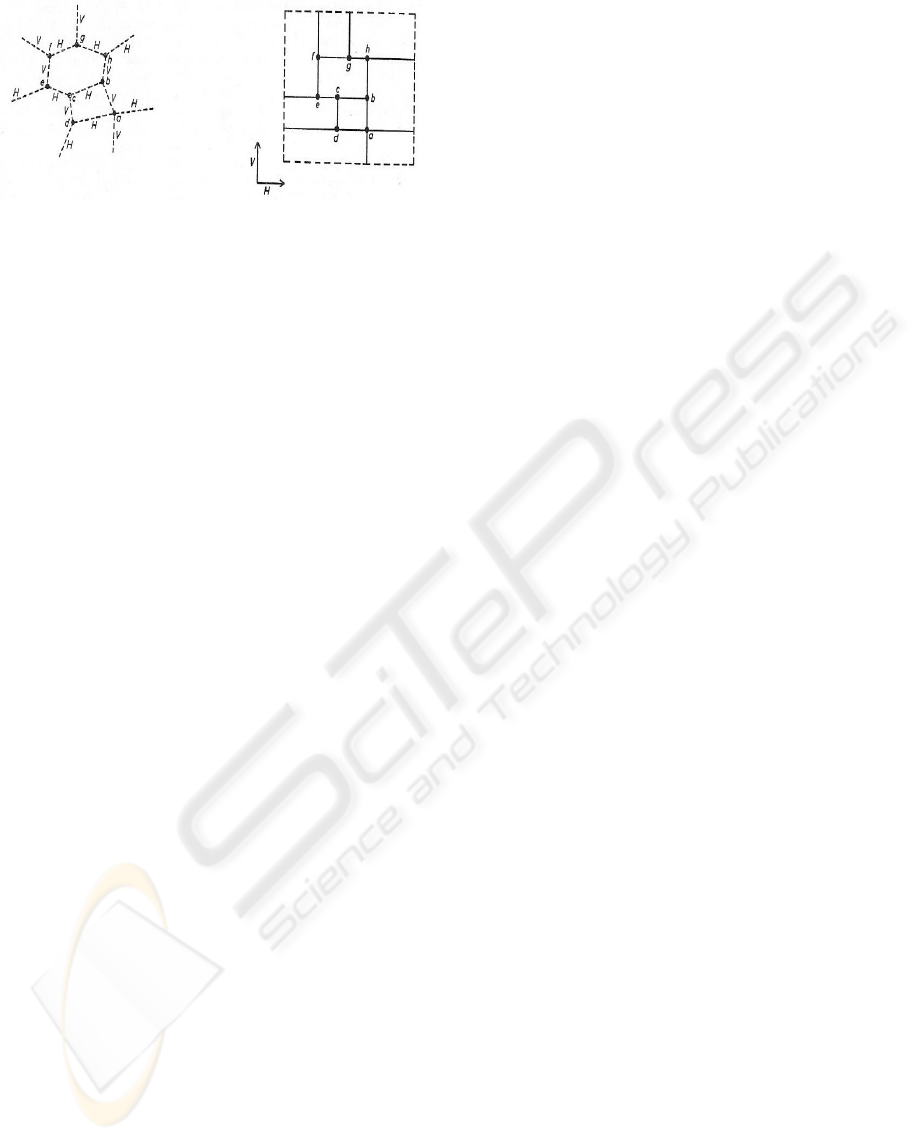
Figure 1: A labelled graph and its associated layout.

produce a declarative implementation solution with

classical programming languages.

However, approximately thirty years after, we

have available today more and better (declarative)

tools and resources and in particular logical and pro-

cedural mechanisms to more easily develop such an

implementation. For a single comparison, the solu-

tion deﬁned in (Pereira, 1974) was indeed completely

implemented in Algol68, having the author even to

implement his own backtracking mechanism at a high

level. Since then, possibly many solutions were im-

plemented in various other languages, but here we

are proposing a solution based not in one but in two

distinct logic programming frameworks and their im-

plementations (XSB-Prolog and Smodels) aiming at a

cooperative chore division that makes use of the better

strengths of each.

Additionally, since the appearance of the Stable

Models Semantics few signiﬁcantly pre-existing com-

plex problems have been considered that can effec-

tively test its strengths and weaknesses. The present

pre-existing combinatorial problem is perfect for that

testing. It is sufﬁciently complex in some of its sub-

problems, thereby allowing the latter semantics to

be tested thoroughly and hence stress its strengths,

and in other of its subproblems too complex or even

too unfeasible to even apply that semantics, resort-

ing then to XSB-Prolog and its Well-Founded Seman-

tics and therefore stressing the former’s weaknesses.

And vice-versa, exchanging the roles of the two se-

mantics. The use of the Stable Models Semantics

was enacted through the XASP interface included in

XSB-Prolog. The interface syntax can be consulted

in (XASP, 2005). More detailed information will be

provided in subsequent sections regarding subprob-

lem solving, namely where each of the semantics is

called for.

In the next section detailed information will be

provided about the problem statement, including hy-

potheses deﬁnition, problem decomposition, and im-

plementation details. There follow, in subsequent

sections, a concise analysis regarding both semantics

and, in the last section, we set forth closing remarks

and future enhancements about the application herein

reported.

2 PROBLEM FORMULATION

AND DECOMPOSITION

The initial problem formulation is deﬁned by the

original deﬁnitional hypotheses presented in (Pereira,

1974), recapped in (Pereira, 1978). Below are those

covered by the current implementation relative to sub-

problem 1.4 deﬁned in (Pereira, 1974; Pereira, 1978),

which establishes the conditions under which a pla-

nar rendering of the adjacency graph gives at least one

permissible hv-assignment:

• Conditions A [These we presuppose]

1. The adjacency graph is ﬁnite, simple, con-

nected, non-separable, and planar.

2. Every interior node of the adjacency graph has

four or more edges.

3. Every face of the adjacency graph must be tri-

angular or rectangular.

• Conditions B [These we wish to satisfy non-

deterministically]

1. Each edge must be labelled or ”coloured” ei-

ther with ’v’ or ’h’, an hv-assignment being a

complete labelling of the graph.

2. No triangular face can have all its edges as-

signed the same colour.

3. All rectangular faces must have opposite edges

assigned the same colour, and non-opposite

ones assigned different colours.

4. The edges around an interior node must be

coloured in such a way that they may be

grouped into four successive alternating colour

groups.

The implementation approach was decomposed

into the following subproblems and attending em-

ployed technology:

1. To determine the set of faces formed by the adja-

cency graph (XSB-Prolog).

• Deﬁne triangle as a set of 3 pairwise adjacent

nodes

• Deﬁne square as a sequence of 4 nodes where

each each node is adjacent only to its predeces-

sor and its sucessor

• Deﬁne a shape starting at a given node as a tri-

angular or square face having that node as a ver-

tex.

ICEIS 2007 - International Conference on Enterprise Information Systems

364

• Obtain all the shapes, starting from a given

node as the set of all faces having that node as

a vertex.

2. To determine the labelled hv-graph given the set

of faces (Smodels).

• Deﬁne color as being an ’h’ or a ’v’.

• Deﬁne arc as a directed adjacency.

• Deﬁne a coloured arc as an arc with a assigned

color.

• There can be no stable model where an arc has

more than one labelling.

• There can be no stable model where both arcs

that deﬁne an adjacency have different labels.

• There can be no stable model where every arc

that constitutes a triangle have been coloured in

the same way.

• There can be no stable model where opposite

arcs constituting a square are coloured in the

same way.

3. To determine the two, horizontal and vertical,

space partitions given the hv-graph (XSB-Prolog).

• Orient each label given a permissible hv-

assignment as mentioned in (Pereira, 1974),

Chapter 6, Section 2 and in (Pereira, 1978),

namely, every edge in the same colour group

of any node must be directed in the same sense

and opposite groups must have their edges op-

positely directed with respect to the node.

• Obtain the set of paths from every initial or

source node to each terminal or sink node.

4. To determine the minimal modular dimensions for

each space given the partitions (XSB-Prolog).

• A node’s minimal X dimension is the number

of its occurrences in the vertical partition.

• Similarly, a node’s minimal Y dimension is the

number of its occurrences in the horizontal par-

tition.

5. To determine the coordinates positioning each

space. (XSB-Prolog)

• Implement both contour recognition automata

proposed in (Pereira, 1974), Chapter 6, Section

2 and (Pereira, 1978).

• The ﬁrst automaton tries to determine the coor-

dinates of the external divisions, thus giving a

boundary for the interior nodes.

• The second automaton starts with any unpro-

cessed node adjacent to at least one of the pre-

viously processed nodes and computes the co-

ordinates of the next division and the next di-

rection.

Figure 2: a) Adjacency graph. b) Coloured Adjacency

graph.

• So, ﬁrst determine the coordinates for all exte-

rior nodes thus obtaining an external skeleton

for the layout.

• And secondly, having the external skeleton de-

termine the coordinates for the interior nodes.

6. To draw the ﬁnal layout (XSB-Prolog).

• Generate an empty matrix given all dimensions.

• Sweep each line, ﬁlling each cell with the cor-

responding space ﬁguring at that coordinate.

The solution is almost entirely based on that pro-

posed in (Pereira, 1974), complemented with a few

enhancements for integration of two distinct types of

semantics, the Well-Founded Semantics (WFS) and

the Stable Models (SM) one.

As an example consider the adjacency graph ex-

hibited in Fig.2a, regarding the topology of 14 spaces

where the graph is compliant with Conditions A from

the start.

From the graph one can easily obtain all the faces

where a given node appears. For instance, taking node

10 as the starting node we can obtain 5 faces, namely a

triangle formed together with nodes 1 and 9, a triangle

formed together with nodes 1 and 2, a third triangle

formed together with nodes 2 and 3, a square formed

together with nodes 9, 8 and 11, and ﬁnally another

square formed together with nodes 3, 4, and 11.

Having the faces where every node appears, one

can now label each edge in the graph with either an

’h’ or a ’v’, so long as the restrictions presented in

Conditions B are veriﬁed. One colouring for the ad-

jacency graph presented is depicted in Fig.2b.

Having the hv-graph, we proceed to determine

the horizontal and vertical partitions of the graph.

The horizontal partition can be obtained by consid-

ering a subgraph of the hv-graph whose edges are just

those labelled with ’v’; similarly the vertical partition

can be obtained considering only those edges labelled

with ’h’.

Given the colouring depicted in Fig.2b, the hor-

izontal partition of the hv-graph with a possible de-

ﬁned direction for each edge is consummated in

ARCHITECTURAL DESIGN VIA DECLARATIVE PROGRAMMING

365

Figure 3: a) Horizontal partition graph. b) Vertical partition

graph.

Fig.3a. Similarly, the vertical partition is depicted in

Fig.3b.

Given the horizontal and vertical partitions of the

hv-graph, we now determine the set of paths from ev-

ery initial node to every terminal node in each parti-

tion, with arbitrary directions. Starting with the hor-

izontal partition, the table of columns, i.e, the set of

all paths is (each path is represented as a column) is

on the left; for the vertical partition, the table of rows,

i.e, the set of all paths is (each path is represented as

a row) is on the right:

1 1 2 2 3 1 2 3

9 9 10 10 4 1 10 3

8 8 11 11 5 9 10 3

7 12 13 13 8 11 4

14 14 5 7 12 13 4

6 6 7 14 5

7 6 5

For the subproblem of determining the minimal

modular dimensions of each space it sufﬁces to count

the occurrences of each division in the table of

columns thus determining their minimal X-coordinate

dimension and, similarly, counting its occurrences

in the table of rows to determine the minimal Y-

coordinate dimension.

Table 1 shows the minimal modular dimensions

for each division for the example under consideration.

At this point, there just remain to be determined

the coordinates of the spaces. As mentioned earlier,

the exterior nodes’ coordinates are computed ﬁrst,

thus obtaining the external skeleton of the layout, and

only then the interior nodes’ coordinates are calcu-

lated, as all their hv-graph ancestor’s coordinates have

been calculated.

To obtain the ﬁnal layout it sufﬁces to build the

matrix whose dimensions can be calculated with each

node’s coordinates and minimal modular dimensions,

and then to put each division in the matrix.

Fig.4 depicts one of the layouts obtained from the

initial adjacency graph with a 90 degree symmetric

turn of the permissible hv-assignment that was pre-

Table 1: Minimal modular dimensions.

Space X dimension Y dimension

1 2 2

2 2 1

3 1 3

4 1 2

5 2 2

6 2 1

7 1 3

8 2 1

9 2 1

10 2 2

11 2 1

12 1 1

13 2 1

14 2 1

Figure 4: Layout.

sented in this section. Other examples are presented

in Figs. 5 and 6.

In the next sections an overview of each logic pro-

gram semantics’ implementation adequateness is ex-

amined.

3 WELL-FOUNDED SEMANTICS

TABLED DERIVATION -

XSB–PROLOG

The XSB–Prolog system implements the Well-

Founded Semantics (WFS) (Gelder et al., 1991) par-

tially by means of a tabled loop detection and de-

laying mechanism. The loops in the program are

then solved with the undeﬁned truth-value — just

like WFS does. Taking advantage of the underlying

WFS implementation, the XSB–Prolog system can be

safely used for top-down query solving with no risk

of falling into a endless loop like a normal Prolog

Figure 5: Another layout for the same graph.

ICEIS 2007 - International Conference on Enterprise Information Systems

366

Figure 6: Non-rectangular layout (with black external

space) still for the same graph.

implementation would. The default negation of the

Well-Founded Semantics is the more adequate one to

express most of the constraints regarding the permis-

sible layout schemes in this problem. For example,

the two alternative edge colourings of each edge are

expressed by means of a length 2 even loop over de-

fault negation, and WFS is able to cope with them.

Indeed, we rely on XSB–Prolog to compute the resid-

ual or kernel program of a query, and on Smodels to

compute the Stable Models of this kernel. The XSB–

Prolog XASP interface — as it is known — provides

an ASP interface which permits the programmer to

call on the Smodels implementation. In summary, the

XASP side of the implementation top-down ﬁnds ex-

actly just those default negation literals involved in

loops which are relevant for the query, and then the

Smodels part takes such even loops remaining to be

solved, plus any integrity constraints, and returns their

solutions, i.e. their Stable Models, back to XASP for

integration into answers to the query.

Top-down querying, in general, can improve the

level of groundness of the residual program pertaining

to a query. It thus avoids some of the complications

that full groundness, required of the whole program

and not just the residual part with respect to the query,

begets for problem representation when just Stable

Models implementations are used. Because it can do

without full groundness of the whole program, pro-

gramming with meta-interpreters becomes a usable

tool, that enlarges the degree of freedom in represent-

ing and solving problems, compared with the Stable

Models implementations.

However, it is also true that the deﬁnition of many

of the more complex concepts in the theory ended

up being expressed with several procedural consid-

erations in mind, for efﬁciency reasons. Pure logical

declarativeness is not always desirable for that reason,

and this shortcoming is clearly expressed by some of

the more complex parts of the developed program.

The main advantage of a tabulated implementa-

tion of WFS is the computational efﬁciency of the

derivation algorithm, which is polynomial. Well-

established implementations, like XSB–Prolog, can

interact with several other logic programming tools

and external applications, and provide adequate con-

structs to allow for a ﬂexible user interface, in addi-

tion to debugging tools.

Our program is almost entirely based on XSB–

Prolog, in part because some of the subproblems can

easily be implemented with the WFS semantics, or

the SLDNF (negation by failure) semantics, which is

also available in XSB–Prolog. For other subproblems

Smodels is the perfect choice; then the XSB–Prolog

side prepares all the data to be sent to Smodels, by

building the residual program, sending it to Smodels,

obtaining the results back and interpreting them.

4 ANSWER SET SEMANTICS -

SMODELS

The answer set semantics is a popular choice in the

logic programming community, that allows for im-

proved ways to declaratively express problem solving

theories, and a method to compute their correct solu-

tions.

Logical expressiveness is greatly enhanced by the

introduction of explicit negation and a more intuitive

way to express problem related constraints and to gen-

erate all possible models for a given theory. The sub-

problem related with the determination of permissi-

ble hv-assignments, for instance, is easily expressed

in the answer set semantics, without much complex-

ity in the development of the program.

There are some main disadvantages however, that

constitute the major drawbacks of the answer set se-

mantics approach. The ﬁrst one, related to the non-

relevancy property, is the computational complexity

of the model derivation, which belongs to the NP-

complete class of problems. As such, its implemen-

tations have an exponential temporal complexity to

compute all the answer sets.

Secondly, Stable Models in non-cumulative, thus

being unable to make use of already known sets of

literals, something that could easily be used for the

instance of the problem at hand.

The third disadvantage refers to the way all its im-

plementations, like Smodels, treat a program. The

stable models (and answer sets) semantics considers

the whole Herbrand base of a logic theory i.e., it only

works with fully instantiated rules. Before compu-

tation of the stable models begins, it is necessary for

the implementation to combine the substitutions of all

variables in a rule, with respect to all possible ground

instance values of each one.

As a consequence of some of the previous dis-

advantages, Smodels cannot make use of known de-

terministic properties of our layout theory. For in-

stance, while XSB-Prolog, enhanced with a deter-

ARCHITECTURAL DESIGN VIA DECLARATIVE PROGRAMMING

367

ministic priority meta-interpreter mechanism (like the

one deﬁned in (Pereira et al., 1992)), can, without

grounding, identify each deterministic call in turn,

and therefore produce an evaluation in polynomial

time without recourse to backtracking, Smodels in-

stead is forced to ground every variable in the pro-

gram, having even to resort to each variable’s domain

to do so. Meta-interpretation allows guiding an eval-

uation without the spacial multiplication of the pro-

gramme, and without analyzing each variable’s do-

main, a priceless feature when integrated into XSB-

Prolog.

It is also not possible to deﬁne dynamic constructs

during computation, which greatly limits expression

of certain aspects of the theory. These limitations

were deeply felt during development of this imple-

mentation and greatly conditioned the use of this se-

mantics throughout.

These disadvantages had a direct impact in the

process of choosing the tool in which to implement

each of the referred subproblems or, more appropri-

ately, in preferring XSB–Prolog over SModels, even

for the combinatorial ones. For instance, the dynamic

construct deﬁnition disadvantage is patent in subprob-

lem 1, in the problem of determining the horizontal

and vertical partitions of the hv-graph, and in deter-

mining the minimal modular dimensions of each di-

vision, simply because it cannot be known a priori the

exact number of elements we are referring to, and,

even if they were known, it would probably be very

difﬁcult to code anyway. On top of that, the derivation

algorithm can transform a polynomial problem into

an exponential one, as exempliﬁed by subproblem 5

related to the determination of the coordinates of the

external skeleton of the layout, which can be solved

in polynomial time and, if translated into SModels,

would turn exponential.

5 CLOSING REMARKS AND

FUTURE WORK

The implementation presented in this article corre-

sponds only to a limited subset of the rather com-

plete theory presented in (Pereira, 1974). As men-

tioned earlier, only the planar topological aspect of

the problem-solving theory was considered, i.e. a

planar rendering of the graph was assumed. The ex-

tensions required to restrain the dimensions of each

space and each adjacency to speciﬁed intervals were

clearly out of scope of this work, but they are unavoid-

able in order to obtain a practical and general usable

solution to the problem.

Only one of the subproblems mentioned was im-

plemented in Smodels; however, also the subprob-

lem related to determining the orientation of the la-

bels could be implemented in it. This subproblem, as

implemented in XSB–Prolog, is one of the most com-

plex parts of the program and, if it were implemented

in Smodels, the relevant part of the code would be

much more concise, logical and substantially reduced

in size and complexity. Unfortunately, because of the

disadvantages mentioned, we found the time com-

plexity of the obtained code substantially increased,

as did the number of layouts obtained, but unneces-

sarily since the new solutions are just symmetrical

variations! For example, given a triangular adjacency

graph, the distinct number of solutions (modulo sym-

metry) is 6 in the current implementation, but would

turn to 24 if developed in Smodels, with no really new

solutions.

A possible solution for this problem is in the uti-

lization not of the usual Stable Models Semantics but

of a revised one, which enjoys relevancy and cumula-

tivity, as mentioned and deﬁned in (Pereira and Pinto,

2005a) and (Pereira and Pinto, 2005b), which are

properties required for an efﬁcient and more declar-

ative implementation for the instance at hand.

Regarding the generalization of the problem in-

stance tackled, future work includes dynamically ob-

taining alternative planar representations of an adja-

cency graph, albeit from an initially non-planar one,

respecting some constraints, and so allowing for a

more ﬂexible interface with a human user, who does

not have to produce a planar representation; addition

of range intervals for each dimension, thereby restrict-

ing the possible values associated with each space and

taking a signiﬁcant step towards real requisites; al-

lowing dimensional range overlap of spaces in order

to view and detect problematic design points; intro-

duction of layout restrictions guaranteeing elimina-

tion of unwanted layouts; interconnection with Auto-

CAD, thus enabling a more formal presentation of the

layouts, which are currently represented in HTML.

This application is a perfect example of the ben-

eﬁts of a joint collaboration of the Well Founded Se-

mantics and the Stable Models Semantics aiming at

theory building for problem solving.

Having implemented the solution in this hybrid

way we can thus gain more declarativeness by rele-

gating every task to the system where we can more

easily programme it and, also obtaining a much more

efﬁcient solution by relegating each task to the system

that more easily solves it.

Future research in this double approach can un-

doubtedly provide a more declarative, simple and

logical approach to problems on the basis of Logic

Programming. Some major steps have already been

ICEIS 2007 - International Conference on Enterprise Information Systems

368

taken towards that direction, namely the revised Sta-

ble Models Semantics presented in (Pereira and Pinto,

2005a) and (Pereira and Pinto, 2005b), as it is be-

lieved that enhancements to the Stable Models se-

mantics can bring major improvements to the ﬁeld of

Logic Programming.

ACKNOWLEDGEMENTS

We thank Andr

e Costa, Gonc¸alo Lopes and Alexandre

Constantino for their help.

REFERENCES

Gelder, A. V., Ross, K. A., and Schlipf, J. S. (1991). The

well-founded semantics for general logic programs.

Journal of the ACM, 38(3):620–650.

Pereira, L. M. (1974). Layout Schemes From Adjacency

Graphs — a case study in problem solving by the-

ory building. PhD thesis, Brunel University UK, pub-

lished by Laborat

orio Nacional de Engenharia Civil

(LNEC) Lisbon.

Pereira, L. M. (1978). Artiﬁcial intelligence techniques in

automatic layout design. In Artiﬁcial Intelligence and

Pattern Recognition in Computer Aided Design, pages

159–173. North-Holland.

Pereira, L. M., Alferes, J. J., and Dam

asio, C. (1992). The

sidetracking meta-principle. Simp

osio Brasileiro de

Intelig

encia Artiﬁcial, pages 229–242.

Pereira, L. M. and Pinto, A. (2005a). Implementing the re-

vised stable models — an ASP-based approach. Sub-

mitted to Annals of Mathematics and Artiﬁcial Intelli-

gence.

Pereira, L. M. and Pinto, A. M. (2005b). Revised stable

models — a semantics for logic programs. In Progress

in Artiﬁcial Intelligence — Procs. 12th Portuguese

Intl. Conf. on Artiﬁcial Intelligence (EPIA’05), LNAI

3808, pages 29–42. Springer.

XASP (2005). XASP: Answer set programming with XSB-

Prolog. http://xsb.sourceforge.net/packages/xasp.pdf.

ARCHITECTURAL DESIGN VIA DECLARATIVE PROGRAMMING

369