A NEW LOOK INTO DATA WAREHOUSE MODELLING

Nikolay Nikolov

European Bioinformatics Institute, Wellcome Trust Genome Campus – Hinxton, Cambridge, United Kingdom

Keywords: Data Warehouse modelling.

Abstract: The dominating paradigm of Data Warehouse design is the star schema (Kimball, 1996). The main debate

within the scientific community for years has been not whether this paradigm is really the only way, but,

rather, on its details (e.g. “to snowflake or not to snowflake” – Kimball et al., 1998). Shifting the emphasis

of the discourse entirely within the star schema paradigm prevents the search for better alternatives. We

argue that the star schema paradigm is an artefact of the transactional perspective and does not account for

the analytic perspective. The most popular formalized method for deriving the star schema (Golfarelli et al.,

1998) underlines just that by taking only the entity-relationship-model (ERM) as an input. Although this

design approach follows the natural data and work-flow, it does not necessarily offer the best performance.

The main thrust of our argument is that the query model should be used on a par with the ERM as a starting

point in the data warehouse design process. The rationale is that the end design should reflect not just the

structure inherent in the data model, but also that of the expected workload. Such approach results in a

schema which may look very different than the traditional star schema but the performance improvement it

may achieve justifies going off-the-beaten track.

1 INTRODUCTION

The purpose of a data warehouse is to store data

which is not involved in current transactions. Such

data is not expected to change often and this is why

(Inmon, 1996) refers to this data as “time-invariant”.

The “time-invariance” is reflected in the star schema

paradigm which dominates the data warehouse

modelling since the emergence of the data

warehouse concept. The star schema refers to one or

more fact tables and several dimension tables which

are connected to the fact table(s) via foreign key

relations. The “time-invariance” allows a relaxation

of the restrictions of the normalized schema design

to merge data connected via functional

dependencies. A well-formalised method of deriving

such a schema was proposed (Golfarelli et al., 1998)

and now is the standard technique of data warehouse

modelling. It takes as input the entity-relationship

model from which the data originates and involves

iterative pruning and merging which result in a de-

normalized scheme. This technique, however, is

only a half-step in the process of emancipating the

data warehouse design from that of the database

design. What is missing in the picture is the query

model. The possibility for queries is the only

rationale for the existence of data warehouses - if we

are not going to manipulate the data, than the only

other meaningful use is to read it. On this

background, it is strange that the currently most

popular method does not consider the query

workload. An important assumption underlies this

omission. It is that we either already know what will

be queried (and this is exactly what is put together in

the fact tables) or that there is no way to know it.

Needless to say, real life offers less clearly cut

situations. While sometimes the workload is really

well known in advance (this is the case with many

commercial reporting applications) in most cases

only vague ideas about the workload exist. For such

applications the ubiquitous star schema may,

actually, be a suboptimal solution. In this paper we

focus on this case and propose an alternative design

approach which incorporates both the underlying

data model and whatever expectations about the

workload might exist. We show that such an

approach results in dramatic performance

improvement compared to the classical star schema

using the same amount of storage. We propose a

simple yet efficient algorithm which can be used to

derive such a schema. Our paper is organised as

follows: in Part 2 we present our method, in Part 3

we compare the runtime performance of our method

to that of the traditional star schema design using the

TPC-H benchmark, in Part 4 we give brief account

540

Nikolov N. (2007).

A NEW LOOK INTO DATA WAREHOUSE MODELLING.

In Proceedings of the Ninth International Conference on Enterpr ise Information Systems - DISI, pages 540-543

DOI: 10.5220/0002347205400543

 SciTePress

of the related literature, in Part 5 we give conclusion

and outlook.

2 CONSTRUCTING A

FRAGMENTED SCHEMA

Proto-queries as “vague queries”

As already discussed, in many cases the data

warehouse designer has only vague expectations

about the future workload. These expectations may

be based on one or more of the following sources:

• past workload traces

• metadata (attributes fitting logically together)

• domain expertise.

To keep the setting as general as possible, we

assume that only probabilistic attribute associations

are available at this stage. This means that no

preferences exist for specific attribute values (i.e. the

January sales are more interesting and likely to be

queried than the May sales). These expectations are

formalized as a set Q of “proto-queries” q

, each

weighted by the probability p

of its occurrence.

Trade-off between storage and performance

In an ideal world the tables in the final model

exactly match the future queries. But in reality there

is a sizeable mismatch resulting in joins (when the

query includes attributes not in the same table) or

overhead I/O (when the table includes attributes

which do not appear in the same query) both of

which have negative impact on the performance.

One solution to avoid them is to create a table for

each proto-query. The problem is that even for

modest entity-relationship and query models this

approach would require too much storage. Ideally,

we would “translate” both the joins and the overhead

I/O into one single unit which we would aim to

minimize while satisfying the storage constraint.

However, there is no constant “exchange rate”

between the joins and the excessive I/O in terms of

the read operations involved or the resulting query

duration. Therefore, to simplify the problem, we will

regard the number of joins as a constant which is

determined by both the query and entity-relationship

model (i.e. the number of joins is the same as in the

case where the queries are executed against the

original ERM). So the only thing which we aim to

optimize is the excessive I/O.

Data Warehouse modelling as a knapsack problem

This optimization task is an instance of the knapsack

problem, a NP-hard problem (Martello et al., 1996).

We address it with a simple but effective greedy

heuristic which takes as an input the set of all table

fragments F and their storage requirements.

The Fragment: intersection of a query and a table

A table fragment f

is defined as the intersection

between the attributes of a table t

from the set T of

all tables from the ERM and the attributes accessed

by a proto-query q

= t

i ∩

, t

∈ T, q

∈

Q).

Fragments produced as intersection of the same table

with different queries are called related fragments.

Greedy merge of related fragments

The main idea of the algorithm GreedyMerge (fig. 1)

is to iteratively pair-wise merge related fragments

which are closest to each other until a storage

constraint is met.

algorithm GreedyMerge

input: available storage, set of all fragments F

output: table definitions

1. until (storage constraint is satisfied) loop

2. {for all pairs of related fragments in F

4. {ComputeMergeBenefit

5. merge (pair with max MergeBenefit)}

Figure 1: Pseudocode of the GreedyMerge algorithm.

MergeBenefit as closeness metric

The closeness metric MergeBenefit computed by the

ComputeMergeBenefit algorithm (line 4, fig. 1) is the

ratio of the storage S saved and the increase in I/O

overhead I caused by the merge of the pair of related

fragments f

and f

, weighted by the probabilities of

their proto-queries. Both S and I are sums of length

in bytes of attributes, S of the attributes shared by f

and f

, I of those not shared (fig.2).

Algorithm ComputeMergeBenefit

Input: fragments f

≠ f

- related, i.e. corresp. to

same table t

but to diff. proto-queries q

and q

)

Output: MergeBenefit(f

, f

)

Let O

be the row overhead (DBMS-specific)

be the probability of proto-query q

be the length of attribute a in bytes

= O

// min. storage saving = row overhead

1. for all attributes a

∈

2. { if (a ∉ f

) {I

= I

+ l

} else { S

= S

+ l

}}

3. for all attributes a

∈

4. { if (a ∉ f

) {I

= I

+ l

}}

5. return p

(S/I) //I=0 only if f

≡ f

Figure 2: Pseudocode of ComputeMergeBenefit.

The code displayed in fig. 2 is a slightly simplified

version as it implies that the fragments are “single”

(i.e. correspond to only one proto-query). As the

algorithm progresses, however, “combined”

fragments emerge which consist of several related

A NEW LOOK INTO DATA WAREHOUSE MODELLING

541

single fragments (each corresponds to an

intersection of the same table with a different proto-

query) and so when the fragments

is a combined

fragment, then lines 3-4 change:

3. for all attributes a ∈ f

3.5. { for all constituent fragments of f

4. { if (a ∉ f

) {I

= I

+ l

}}

Figure 3: Computing the overhead I/O in case of a

combined fragment.

The same change applies to lines to lines 1-2 when

is a combined fragment.

The GreedyMerge algorithm has complexity of

O(q

)t where q is the number of proto-queries and t

– the number of tables in the ERM which means that

even for quite big models, the algorithm takes only

seconds to finish. Depending on the value of the

storage constraint its output could be the original

ERM (if the storage constraint is too low for any

redundancy) or a table model consisting of the full

set of F (if the storage is enough to materialize all

fragments).

3 TPC-H AS EXAMPLE

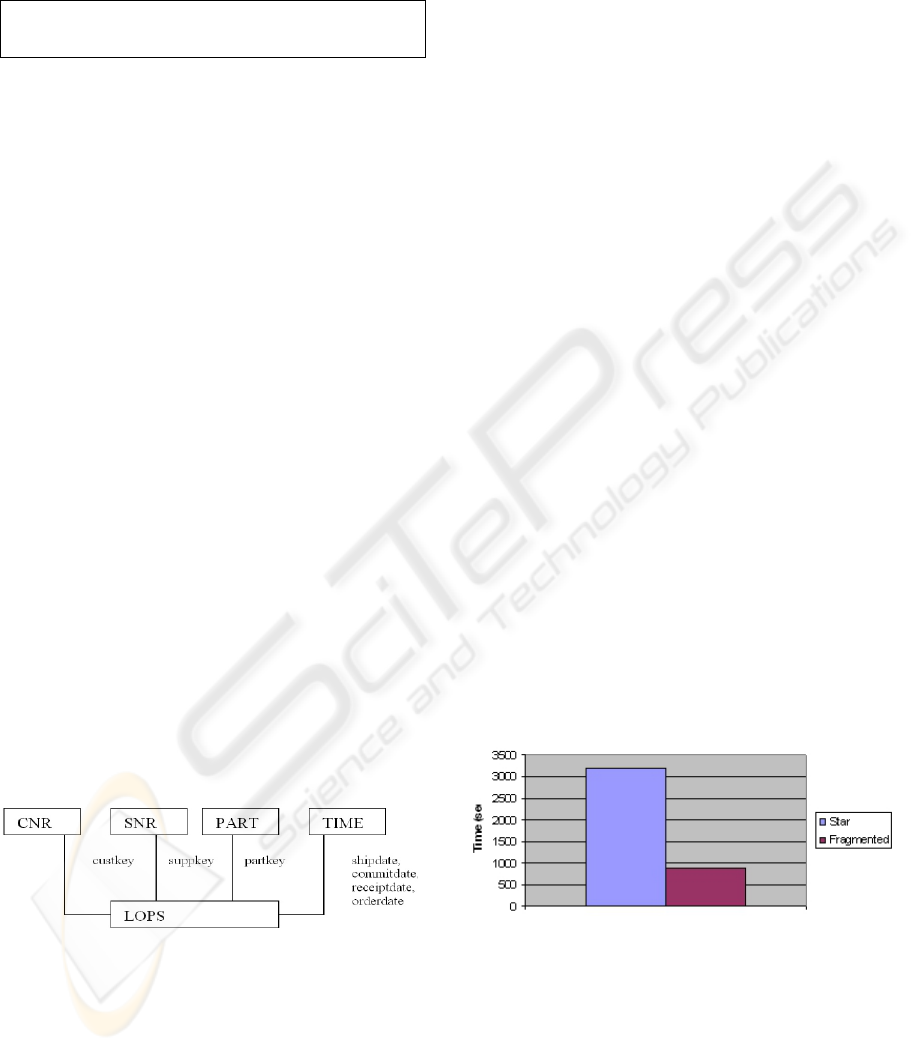
Constructing the Star schema for the comparison

We tested our method using the TPC-H benchmark

(TPC-H, 2002). We constructed a star schema by

merging the tables Lineitem, Orders, PartSupp in a

single table (LOPS), adding the Nation and Region

data to the Supplier and Customer tables (tables

SNR, CNR) and adding a table for the time

dimension (fig. 4). We also let the Oracle 10G

analyze the schema and by providing the TPC-H

queries as input for its Index Advisor we let it also

construct all the indexes it considered useful.

Figure 4: Star schema based on the TPC-H schema.

Constructing the Fragmented schema

As input for the GreedyMerge algorithm we

generated the fragment set F by treating all TPC-H

queries as proto-queries (ignoring the WHERE,

ORDER and GROUP-clauses) all weighted with

probability 1. The result was a set F of 288

fragments which would occupy approximately 4

times more storage than the original TPC-H schema.

We started the GreedyMerge algorithm with the 288

fragments as input and with the storage occupied by

the tables and indexes of the star schema as a storage

constraint, so both the star schema and the

fragmented star schema occupied the same storage.

Due to the storage of the star schema being only 1/3

of the storage occupied by the 288 fragments, most

of them had to be merged. The storage constraint

was met and GreedyMerge terminated when there

were only 10 fragments left out of the initial 288.

Seven were, in fact, original tables (Order, Partsupp,

Part, Supplier, Customer, Nation, Region,), the

remaining three being different overlapping sets of

Lineitem attributes. The first (L1) was the fragment

corresponding to query 19 which seems to have least

in common with any of the other queries accessing

Lineitem and so remained “single”, fragment L2

combined the Lineitem columns needed for queries

12, 4, 21, and fragment L3 combined the Lineitem

attributes needed for queries 3, 5, 7, 8, 9 , 10, 14, 15,

17, 18, 20. Both L1 and L2 fragments have one or

more attribute in common with L3 but no common

attribute with each other. Strange as this scheme

might seem, its overhead for the whole TPC-H

workload is just 37% of the overhead I/O of the star

schema – an excellent result given that both occupy

the same storage.

Comparing the read performance of the Star schema

and the Fragmented Schema

We measured the performance of both schemes by

running the benchmark against them on a standard

PC (1.50GHz Processor, 1GB RAM) running under

Windows XP with Oracle 10g. The TPC-H data used

had a scale factor 1 (1GB).

Figure 5: Comparison of the performance of the Star

schema and the Fragmented schema on the TPC-H

benchmark.

The result showed a significant advantage of the

fragmented schema over the star schema (873 sec

average duration of the TPC-H benchmark vs. 3176

sec. for the star schema, i.e. the fragmented schema

is 3.6 times faster). The extent of this superiority

was surprising for us. We analysed the individual

queries and their execution plans and found out that

ICEIS 2007 - International Conference on Enterprise Information Systems

542

approximately 54% of the difference in the average

runtimes is due to the DBMS optimizer choosing to

use index with the star schema where table scan is

faster. We let the DBMS re-analyze the star schema

using a large sample (20%) of the data but, the

behaviour of the optimizer remained unaffected. We

don’t have explanation for it, but even discounting

these 54% as a result of some inconsistency within

the Oracle 10g optimizer (e.g. wrong selectivity

estimates), the remaining advantage of the

fragmented schema over the star schema is still

impressive.

Comparing the update performance of the Star

schema and the Fragmented Schema

We updated 10% of the tuples in the LOPS table of

the star schema and the L1, L2 and L3 fragments of

the fragmented schema. Again, the fragmented

schema offered better performance, however the

difference was negligible – only 8% faster than the

star scheme.

4 RELATED LITERATURE

Related literature includes works on data warehouse

modelling - (Golfarelli et al., 1998; Kimball et al.,

1998; Bizarro et al., 2002), vertical partitioning -

(Papadomano-lakis et al., 2004; Agrawal et al.,

2004) and new storage models – (Stonebraker et al.,

2005). Our work differs from them through one or

more of the following:

• we use query model as input;

• we use overlapping partitioning instead of disjoint

partitioning;

• we focus on reducing the overhead I/O, and not

on minimizing the joins;

• our method allows for storage constraint;

• we focus on the read performance;

• our method is accommodated within the existing

database technology.

We will treat the relevant literature in more detail in

a full text variant of this paper.

5 CONCLUSIONS AND

OUTLOOK

We think that the current paradigm of data

warehouse modelling commits the mistake of

ignoring important information about the future

workload. In this way many opportunities for

performance improvement are wasted. We propose a

simple, yet effective algorithm to derive a more

query-responsive data warehouse schema. The

schema created in this way was found to offer more

than 3 times better read performance using the same

storage as a star scheme.

We are at the start of our research and many

questions are open – “Are there algorithms which

construct even more effective schema (e.g. merge

not just two fragments at a time but more or merge

unrelated fragments)?”, “Can any performance

guarantees be established using reasonable

assumptions (e.g. self-similarity of the attribute

network)?” and others. We hope that other

researchers will find these questions as interesting as

we do.

ACKNOWLEDGEMENTS

I would like to thank Peter Stoehr for his support.

REFERENCES

Agrawal, S., et al., 2004: Integrating Vertical and Hori-

zontal Partitioning into Automated Physical Database

Design. Proc. 2004 SIGMOD Int. Conf. on Manag. of

Data.

Bizarro, P., Madeira, H., 2002: Adding a Performance-

Oriented Perspective to Data Warehouse Design.

Proc. of 4

Int. Conf. on Data Warehousing and

Knowledge Discovery (DaWaK).

Golfarelli, M. et al., 1998 Conceptual Design of Data

Warehouses from E/R Schemes. In Proc. 32th HICSS.

Inmon, W., 1996. Building the data warehouse, John

Wiley & Sons, Inc. New York, NY, USA.

Kimball, R., 1996. The data warehouse toolkit: practical

techniques for building dimensional data warehouses,

John Wiley & Sons, Inc. New York, NY, USA.

Kimball, R. et al., 1998. The data warehouse lifecycle

toolkit, John Wiley & Sons, Inc. New York, NY, USA.

Martello, S., Toth, P., 1990. Knapsack problems:

algorithms and computer implementations, John

Wiley & Sons, Inc. New York, NY, USA.

Papadomanolakis E., Ailamaki, A., 2004: AutoPart:

Automating Schema Design for Large Scientific

Databases Using Data Partitioning. Proc. 16

Int.

Conf. on Scient. and Stat. Datab. Manag. (SSDBM).

Stonebraker, M. et al., 2005. C-Store: A Column-oriented

DBMS. Proc of the 31st Int. Conf. on Very Large

Databases (VLDB).

TPC-H Standard Specification Revision 2.1.0, 2002.

http://www.tpc.org

A NEW LOOK INTO DATA WAREHOUSE MODELLING

543