HEAVYWEIGHT ONTOLOGY MATCHING
A Method and a Tool Based on the Conceptual Graphs Model
Fr
´
ed
´
eric Furst
LARIA, University of Amiens, UPJV, 33 rue Saint Leu - 80039, Amiens, France
Francky Trichet
LINA, University of Nantes, 2 rue de la Houssini
`
ere BP 92208 - 44322, Nantes, France
Keywords:
Heavyweight Ontology, Axioms, Graph-Based Techniques, Ontology Matching, Conceptual Graphs.
Abstract:
Managing multiple ontologies is now a core question in most of the applications that require semantic interop-
erability. The Semantic Web is surely the most significant application of this report: the current challenge is
not to design, develop and deploy domain ontologies but to define semantic correspondences among multiple
ontologies covering overlapping domains. In this paper, we introduce a new approach of ontology matching
named axiom-based ontology matching. As this approach is founded on the use of axioms, it is mainly dedi-
cated to heavyweight ontologies (an heavyweight ontology is a lightweight ontology, i.e. an ontology simply
based on a hierarchy of concepts and a hierarchy of relations, enriched with axioms used to fix the semantic
interpretation of concepts and relations), but it can also be applied to lightweight ontologies as a complemen-
tary approach to the current techniques based on the analysis of natural language expressions, instances and/or
taxonomical structures of ontologies. This new matching paradigm is defined in the context of the Conceptual
Graphs model (CG), where the projection (i.e. the main operator for reasoning with CG which corresponds
to homomorphism of graphs) is used as a means to semantically match the concepts and the relations of two
ontologies through the explicit representation of the axioms in terms of conceptual graphs. We also introduce
an ontology of representation dedicated to the reasoning of heavyweight ontologies at the meta-level.
1 INTRODUCTION
Ontology matching is at the heart of the multiple-
ontology management process that is now a core
question in most of the applications that require se-
mantic interoperability such as the Semantic Web
(Doan and Halevy, 2005; Noy, 2004; Shvaiko and Eu-
zenat, 2005).
The strategies for matching ontologies are quite
diverse: hierarchical clustering techniques, Formal
Concept Analysis, analysis of terminological features
of concepts and relations (i.e. names or natural-
language definitions) or analysis of structure. How-
ever, as recalled in (Gomez-Perez et al., 2003), most
of the works that deal with ontology alignment only
consider lightweight ontologies, i.e. ontologies sim-
ply composed of taxonomies of concepts and tax-
onomies of relations. The most significant example
of this situation is the benchmark used during the
campaigns ”Ontology Alignment Evaluation Initia-
tive” (Ashpole et al., 2005; Benjamins et al., 2006)
(http://oaei.ontologymatching.org/), where the on-
tologies used for the experiments are only lightweight
ones: for instance, the anatomy real world case used
in 2006 covers the domain of body anatomy and con-
sists of two ontologies with an approximate size of
several 10k classes and several dozens of relations,
but none of these two ontologies includes axioms.
Axioms are the main building blocks for fixing the
semantic interpretation of the concepts and the rela-
tions, and this is what differentiates lightweight on-
tologies from heavyweight ontologies. Of course, cur-
rently, there are not so many real-world ontologies
that make substantial use of axioms. However, as in-
troduced by T. Berners-Lee (Berners-Lee et al., 2001)
- ”For the semantic web to function, computers must
have access to structured collections of information
and sets of inference rules that they can use to con-
duct automated reasoning” - we think that the need
to develop heavyweight ontologies, i.e. ontologies
265
Furst F. and Trichet F. (2007).
HEAVYWEIGHT ONTOLOGY MATCHING - A Method and a Tool Based on the Conceptual Graphs Model.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 265-270
DOI: 10.5220/0002348802650270
Copyright
c
 SciTePress

which include axioms used both to represent all the
semantics of a domain D and to conduct automated
reasonings on assertions of D (more precisely, to en-
sure that the correct interpretation to semantics of a
construct will be given at run time, or in logic jargon
to restrict possible interpretations of the construct in
a domain of discourse), will inevitably increase in an
immediate future; this is also clearly demonstrated by
the current W3C trend which aims at standardising a
Semantic Web Rule Language.
The work presented in this paper aims at defin-
ing a new ontology matching approach based on the
explicit use of all the components of a heavyweight
ontology. This approach requires the explicit repre-
sentation of the axioms of the two ontologies (that
are considering for the matching process) at the con-
ceptual level, and not at the operational level as it is
usually the case in most of the works related to on-
tological engineering: for instance in Prot
´
eg
´
e (Noy,
2004), the axioms are directly represented in an oper-
ational form (i.e. rules or constraints with fixed and
predefined operational semantics) by using the PAL
language based on logical expressions.
To represent heavyweight ontologies at the con-
ceptual level, we use OCGL (Ontology Concep-
tual Graphs Language) (F
¨
urst et al., 2004). This
modelling language is based on a graphical syn-
tax inspired from those of the Conceptual Graphs
model (CGs). The CGs model, first introduced by
Sowa (Sowa, 1984), is an operational knowledge
representation model which belongs to the field of
semantic networks. This model is mathematically
founded both on logics and graph theory. Two
approaches for reasoning with CGs can be distin-
guished: (1) considered CGs as a graphical interface
for logics and reasoning with logic and (2) considered
CGs as a graph-based knowledge representation and
reasoning formalism with its own reasoning capabil-
ities. In our work, we adopt the second approach by
using the projection (a graph-theoretic operation cor-
responding to homomorphism) as the main reasoning
operator; projection is sound and complete w.r.t. de-
duction in FOL. The CG model allows us to repre-
sent terminological knowledge through the specifica-
tion of concepts and relations, and to represent both
classical properties (such as subsumption or algebraic
properties) and any kind of axioms at the concep-
tual level. This explicit graph-based representation
of axioms coupled with reasoning capabilities based
on graphs homomorphism facilitates the topological
comparison of axioms. The matching method we
propose mainly relies on this feature: ontology mor-
phism founded on graph-based knowledge represen-
tation and graph-based reasoning mechanisms.
The rest of this paper is organized as follows. Sec-
tion 2 presents the modelling paradigm we advocate
for defining a domain ontology. Section 3 introduces
the basic foundations of our axiom-based matching
method and presents the principles of our algorithm.
Section 4 compares our approach to related work.
2 CONTEXT OF THE WORK
The OCGL modelling language (Ontology Concep-
tual Graphs Language) we use for specifying an on-
tology (at the conceptual level) is based on three
building blocks: Concepts, Relations and Axioms.
Representing an ontology in OCGL mainly consists
in (1) specifying the conceptual vocabulary of the do-
main and (2) specifying the semantics of this concep-
tual vocabulary through axioms (F
¨
urst et al., 2004).
The conceptual vocabulary consists of a set of Con-
cepts and a set of Relations. These sets can be struc-
tured by using both well-known conceptual properties
called Schemata Axioms and Domain Axioms. The
union of these Schemata Axioms and Domain Ax-
ioms corresponds to what we call Axioms.
The Schemata Axioms proposed in OCGL are:
(1) the ISA link between two concepts or two rela-
tions (subsumption property) used to construct con-
cept/relation taxonomies (tree or lattice), (2) the Ab-
straction of a concept, which corresponds to an
Exhaustive-Decomposition in some works (Gomez-
Perez et al., 2003), (3) the Disjointness of two con-
cepts, (3) the Signature of a relation, (4) the Algebraic
properties of a relation (symmetry, reflexivity, tran-
sitivity, irreflexivity, etc.), (5) the Exclusivity or the
Incompatibility between two relations (the incompat-
ibility between R
1
and R
2
is formalized by ¬(R
1
∧R
2
),
the exclusivity is formalized by ¬R
1
⇒ R
2
) and finally
(6) the Cardinalities of a relation.
Domain Axioms correspond to knowledge which
can not be represented with Schemata Axioms (repre-
senting classical properties of concepts or relations).
The OCGL graphical syntax used to express such
an axiom is based on the Conceptual Graphs model.
Thus, an axiom is composed of an Antecedent part
and a Consequent part, with a formal semantics that
intuitively corresponds to: if the Antecedent part is
true, then the Consequent part is true. Figure 1 shows
the OCGL graph representing the axiom ”The enemy
of my friend is my enemy”. Note that this axiom is a
real Domain Axiom because it cannot be represented
by using classical properties, in comparison with the
axiom ”The friend of my friend is my friend” which
is represented by the transitivity of the relation called
Friend(Human,Human) , that is a Schemata Axiom.
ICEIS 2007 - International Conference on Enterprise Information Systems
266

Figure 1: Representation of an axiom in TooCom. The
bright nodes represent the antecedent part, the dark ones
the consequent part. A concept node (indicated by a rect-
angle) is described by a label and a marker that identifies
the considered instance (the marker ∗ denotes an undefined
instance). A relation node (indicated by an ellipse) is only
described by a label. An edge between a concept and a re-
lation is labeled with the position of the concept in the sig-
nature of the relation. The logical expression of the graph
is automatically generated.
OCGL has been implemented in a tool, called
TooCom (a Tool to Operationalize an Ontol-
ogy with the Conceptual Graph Model), dedi-
cated to the edition and operationalization of do-
main ontologies (F
¨
urst and Trichet, 2005b; F
¨
urst
and Trichet, 2005a). TooCom is available un-
der GNU GPL license at the following URL:
http://sourceforge.net/projects/toocom/ .
3 AXIOM-BASED SEMANTIC
MATCHING
The objective of ontology matching is to discover and
evaluate semantic links (e.g. identity or subsump-
tion) between conceptual primitives (concepts and re-
lations) of two given ontologies supposed to be built
on related domains. Our approach relies on the use
of the axiomatic level of the ontologies to discover
semantic analogies between primitives, in order to re-
veal identities between them and to calculate the sim-
ilarity coefficient of these identities, i.e. a coefficient
that indicates how closely two concepts or relations
are related. Of course, using the axiomatic level does
not forbid to use the terminological level; these two
approaches complement each other. Our algorithm
(implemented in the current version of TooCom) takes
as input two ontologies O
1
and O
2
(represented in
OCGL) and provides as output potential similarity be-
tween two concepts or two relations: the result is a
set of matchings (P
i
, P
′
j
,C), where P
i
and P
′
j
are re-
spectively conceptual primitives (concepts and rela-
tions) of O
1
and O
2
, and C the similarity coefficient
between P
i
and P
′
j
. Of course, for a given primitive P
i
of O
1
, several (or any) matchings can exist with prim-
itives of O
2
, and vice versa. Both Schemata Axioms
and Domain Axioms are used to evaluate or discover
primitive matchings.
First, in order to allow the end-user to re-
fine the results of our algorithm according to the
matching context, we have associated a weight
to each OCGL property. These weights can be
modified in order to modulate their influence on
the evaluation of the matching. Thus, there are
parameters of our algorithm which can be changed
to improve the precision of the results. By default,
the values of the weights are ordered as follows:
W
AlgebraicProperties
(W
Sym
,W
Trans
,W
Ref l
,W
Irref
,W
AntiSym
) >
W
Disjointness
= W
Incompabibility
= W
Exclusivity
>
W
Cardinality
m
in
= W
Cardinality
m
ax
> W
Axiom
> W
Signature
>
W
Abstraction
> W
ISA
. Again, this scale of weights is a
just a guess which for us corresponds to a universal
distribution for all ontologies; it can be modified
by the end-user according to the kind of ontologies
which are considered and/or subjective preferences.
Then, to detect analogies between axioms repre-
sented as graphs, and then to detect analogies be-
tween the primitives corresponding to the nodes of
the graphs, the Domain Axioms are transcribed into
a more abstract form, that preserves the topological
structures of the graphs. These abstract represen-
tations are based on an ontology of representation
called MetaOCGL.
Relation
Universal
Concept
binary_relationship
(Universal,Universal)
role
(Relation,Concept)
Algebraic_Property
Symmetry
Transitivity
Reflexivity
Antisymmetry
Antecedent_C
Consequent_C
role1
(Relation,Concept)
role2
(Relation,Concept)
role3
(Relation,Concept)
Property
has_r
(Binary_R,Algebraic_Property)
has_c
(Concept,Abstraction)
Ternary_R
Antecedent_TR
Consequent_TR
Binary_R
Antecedent_BR
Consequent_BR
Irreflexivity
Abstraction
difference
(Universal,Universal)
T
AS
IR
isa
(Universal,Universal)
isa_c
(Concept,Concept)
isa_r
(Relation,Relation)
IR S
disjunction
(Concept,Concept)
exclusivity
(Relation,Relation)
IR S
Symmetry Reflexivity Transitivity
Irreflexivity Antisymmetry
S R
T
IR AS
Binary_R: *
Binary_R: *
isa_r
has_r
Algebraic_Property: *
has_r
1 2 1 2
2
1
Concepts
Relations
Algebraic Property Inheritance
type_identity
(Universal,Universal)
T R S
incompatibility
(Relation,Relation)
IR S
Relation: *
Relation: *
isa_r
exclusivity
1 2 1 2
2
1
Exclusivity Inheritance
Relation: *
exclusivity
Concept: *
Binary_R: *
role_1
1 2 1 2
Binary Signature
Concept: *
role_2
Figure 2: Concepts, relations, Schemata Axioms and Do-
main Axioms of MetaOCGL.
MetaOCGL is the ontology of the OCGL lan-
guage, expressed in OCGL. MetaOCGL can then be
considered as an ontology at the meta-level (Gomez-
Perez et al., 2003). As shown in figure 2, MetaOCGL
includes (1) Concepts, (2) Relations, (3) Schemata
Axioms and (4) Domain Axioms.
HEAVYWEIGHT ONTOLOGY MATCHING - A Method and a Tool based on the Conceptual Graphs Model
267

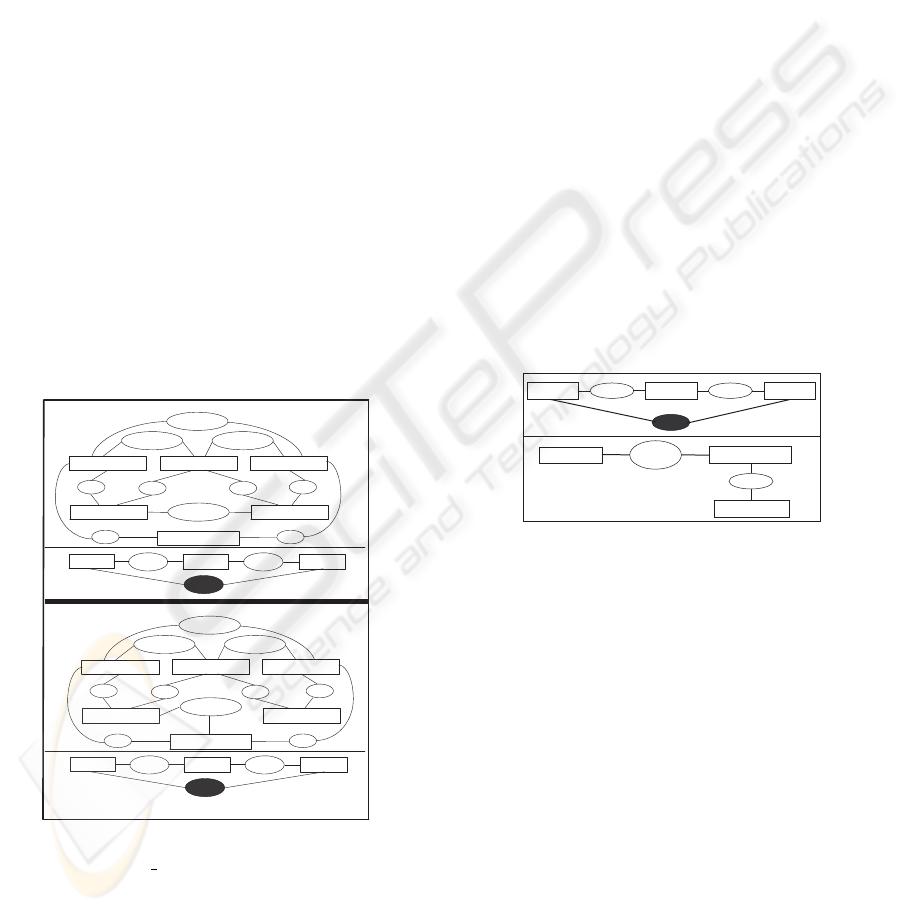
The MetaOCGL Concepts are used to represent
the OCGL primitives: Concept with its two sub-
primitives Antecedent-C and Consequent-C used in
the context of an OCGL Domain Axiom, Prop-
erty which includes the Algebraic-Properties of a
OCGL relation and the Abstraction of a OCGL con-
cept and Relation which again includes the An-
tecedent/Consequent point of view for the differ-
ent kinds of OCGL relations (Binary-R, Ternary-R,
etc.). The MetaOCGL Relations are used to rep-
resent the links between the OCGL primitives: isa
relation which can be stated between two OCGL
concepts or two OCGL relations - the signature is
(Universal,Universal), exclusivity/incompatibility be-
tween OCGL relations, disjointness of OCGL con-
cepts, links between OCGL relations and concepts
in a graph that expresses an OCGL Domain Ax-
iom (type-identity, difference, role). The MetaOCGL
Schemata Axioms are mainly used for describing the
properties of the OCGL relations such as, for in-
stance, the algebraic properties of the isa relationship
(Irreflexivity, Antisymmetry and Transitivity). Finally,
the MetaOCGL Domain Axioms are used to express
the formal semantics of OCGL (for instance, the Al-
gebraic Property Inheritance or the Signature Con-
formity presented in figure 2).
Antecedent_C : *
Antecedent_C : * Antecedent_C : *
type-identity type-identity
type-identity
role1
role2 role1
role2
role1 role2
2 2
2
2
2
2
2
2
1
1
1
1
1
1
1 1
1
Human: *
Human: *
enemy
friend
Human: *
enemy
1 2 1
2
2
1
2
Antecedent_R : * Antecedent_R : *
2
1
type-identity
Consequent_R : *
Axiom
Enemy-
Enemy
in OCGL
Axiom
Enemy-Enemy
in MetaOCGL
Antecedent_C : *
Antecedent_C : * Antecedent_C : *
type-identity type-identity
type-identity
role1
role2 role1
role2
role1 role2
2 2
2
2
2
2
2
2
1
1
1
1
1
1
1 1
1
2
Antecedent_R : * Antecedent_R : *
2
1
type-identity
Consequent_R : *
Human: *
Human: *
enemy
enemy
Human: *
friend
1 2 1
2
2
1
Axiom
Enemy-
Friend
in OCGL
Axiom
Enemy-Friend
in MetaOCGL
Figure 3: Two axioms of OntoFamily represented with
MetaOCGL. The type
identity. links denote the fact that
the nodes of the Domain Axiom (at the domain level) are
similar, i.e. they have the same type. The two graphs (at
the meta-level) are similar without considering type-identity
links, but they differ when considering these links, because
the relations of the antecedent part of the Domain Axiom
”Enemy Enemy” (at the domain level) have the same type,
but not those of the Domain Axiom ”Enemy Friend”.
A domain ontology can be represented as a
MetaOCGL instance (i.e. a MetaOCGL graph), as do-
main facts can be represented by OCGL graphs. The
MetaOCGL graph that represents an ontology con-
tains a part which is dedicated to the representation of
the concept hierarchy, a part which is dedicated to the
representation of the relation hierarchy, and as many
parts as axioms in the ontology. Figure 3 shows the
MetaOCGL graphs dedicated to the representation of
the two axioms of OntoFamily O
1
“The enemy of my
enemy is my friend” and “The enemy of my friend is
my enemy”, and their corresponding meta-graphs in
MetaOCGL. The MetaOCGL representation of an on-
tology expressed in OCGL is automatically provided
by TooCom.
The comparisons between axioms represented in
MetaOCGL are performed by using the projection
operator of the Conceptual Graphs model, a graph-
theoretic operation corresponding to homomorphism
which is sound and complete w.r.t. deduction in FOL.
A projection from a graph G1 into a graph G2 is a
specific morphism of graphs which may restrict the
labels of the vertices; it corresponds to a logical im-
plication between G1 and G2. The figure 4 presents
an example of projection.
Human: * Human: * Human: *
enemy friend
enemy
1 2
2
2
1
1
Man: Romeo
Woman: Juliette
Human: Tybald
hereditary
enemy
friend
1
2
2
1
Figure 4: An example of projection between the Antecedent
part of an axiom and a graph. The axiom is: ”The enemy of
my friend is my enemy”. Its Antecedent part (white nodes
of G1 presented at the top of the figure) can be projected
into the graph G2 (the bottom of the figure), because each
node of G1 has a corresponding node (in G2) that is more
specific than itself: (Human:*) of G1 is more general than
(Man:Romeo) of G2; (enemy) of G1 is more general than
(hereditary enemy) of (G2); etc. In this context, there exists
a projection from G1 into G2. Thus, the axiom can be ap-
plied to G2 to produce the following conclusion: ”Romeo
is the enemy of Tybald”.
Given two graphs G
1
and G
2
, which represent in
MetaOCGL two axioms A
1
and A
2
, if two projections
exist from G
1
into G
2
and from G
2
into G
1
, then A
1
and A
2
have the same structure. In this case, the ax-
ioms A
1
and A
2
express the same type of property, and
the analogy between the two axioms can be extended
to the primitives that appear in the axioms.
ICEIS 2007 - International Conference on Enterprise Information Systems
268

3.1 Algorithm: Principles
3.1.1 Using Schemata Axioms
Schemata Axioms that deal with only one primitive
(i.e. algebraic properties and abstractions) are com-
pared from O
1
to O
2
, in order to discover primitive
matchings. If an algebraic property (resp. an ab-
straction) appears in O
1
for a primitive p
1
and in
O
2
for a primitive p
2
, the coefficient c of the match-
ing (p
1
, p
2
, c), if it exists, is increased by W
Alg
(resp.
W
Abs
). If the matching does not exist, (p
1
, p
2
,W
Alg
)
(resp. (p
1
, p
2
,W
Abs
)) is created. If an algebraic prop-
erty (resp. an abstraction) appears in O
1
for p
1
but
not in O
2
for p
2
(or inversely), the coefficient c of the
matching (p
1
, p
2
, c), if it exists, is decreased by W
Alg
(resp. W
Abs
). If it does not exist, (p
1
, p
2
, −1∗W
Alg
)
(resp. (p
1
, p
2
, −1 ∗ W
Abs
)) is created. A partition (a
partition (Gomez-Perez et al., 2003) is the combina-
tion of the abstraction of a concept (the head) and
the disjointness of its children) is a property which is
more semantically rich than a simple abstraction. So,
if two concepts c
1
and c
2
are respectively the head
concept of a partition in O
1
and O
2
, the coefficient
c of the matching (c
1
, c
2
, c), if it exists, is increased
by 2∗W
Abs
(or decreased by 2∗W
Abs
if only one con-
cept is involved in a partition). If it does not exist,
(c
1
, c
2
, 2∗W
Abs
) (or (c
1
, c
2
, −2∗W
Abs
)) is created.
Schemata Axioms that deal with two primitives
(i.e. disjointness, incompatibility and exclusivity)
are used either to modify the coefficients of existing
matchings, or to create new ones. The coefficient of
a matching whose two primitives are involved in a
disjointness, an incompatibility or an exclusivity is
increased by the corresponding weight (i.e. W
Disj
,
W
Incomp
or W
Exclu
). It is decreased if only one of the
primitive is part of such a property. The matching is
created with the corresponding coefficient if it does
not exist.
Finally, table 1 presents the different actions that
are done when considering the cardinalities. If the
matching between the two considered relations does
not exist when an analogy between cardinalities is
found, the matching is created, with the correspond-
ing coefficient. Only cardinalities of relations with
the same arity are compared.
3.1.2 Using Domain Axioms
Domain Axioms are represented in MetaOCGL in or-
der to compare their structures. For each axiom cou-
ple (a
1
, a
2
), where a
1
∈ O
1
and a
2
∈ O
2
, the rep-
resentations of a
1
and a
2
in MetaOCGL, meta(a
1
)
and meta(a
2
), are built. These representations are
automatically enriched by adding information about
Table 1: Modifications of the coefficient of the matching
(r
1
, r
2
, c) according to the cardinalities of the relations. c
min
and c
max
are the values of cardinalities for the relations (for
a given element of their signatures).
Relation r
1
in O1 Relation r
2
in O2 Action
Min 0 (resp. c
min
> 1) c
min
> 1 (resp. 0) −2∗W
cmin
Card c
min
6= 0 c
min
6= 0 +2∗W
cmin
c1
min
6= 0 c2
min
6= 0 and 6= c1
min
−W
cmin
Relation r
1
in O1 Relation r
2
in O2 Action
Max ∞ (resp. c
max
> 1) c
max
> 1 (resp. ∞) −W
cmax
Card c
max
6= ∞ c
max
6= ∞ +2∗W
cmax
c1
max
6= ∞ c2
max
6= ∞ and 6= c1
max
−2∗W
cmax
the nodes: for instance, in figure 3, the two rela-
tions enemy of the axiom Enemy-Enemy in OCGL
are represented in MetaOCGL by the two concepts
Antecedent
R which are linked by the meta-relation
called type
identity, because the antecedent part of the
Domain Axiom Enemy-Enemy in OCGL includes two
instances of the same relation Enemy.
Two types of topological equivalence are then
considered:
1. the Equivalence, that occurs when projections
exist from meta(a
1
) to meta(a
2
) and from
meta(a
2
) to meta(a
1
), without considering the
type
identity relations;
2. the Typed-Equivalence that occurs when the two
projections exist with the type identity relations.
The weight of a typed-equivalence is higher than
those of an equivalence. A typed-equivalence (resp.
equivalence) between two axioms increases the coef-
ficient of nodes linked by projection by the weight
of the axiom typed-equivalence (resp. equivalence).
When no projection (or only one) exists, no modifica-
tion is done.
For example, the two Domain Axioms of figure 3
(Enemy-Friend and Enemy-Enemy) are equivalent be-
cause two projections exist between their meta-graphs
without considering the type-identity relations. When
considering the type-identity relations, there exists no
projection, so they are not typed-equivalent.
4 RELATED WORK
Currently, a lot of tools that deal with finding corre-
spondences between ontologies are proposed (Doan
and Halevy, 2005; Noy, 2004; Shvaiko and Euzenat,
2005). The first way to classify these tools is to con-
sider the objective which is pursued: (1) merging two
ontologies to create a new one, (2) defining a transfor-
mation function that transforms one ontology into an-
other or (3) defining a mapping between concepts or
relations in two ontologies by finding pairs of related
concepts/relations. Our work is dedicated to the latter
HEAVYWEIGHT ONTOLOGY MATCHING - A Method and a Tool based on the Conceptual Graphs Model
269

objective. Note that although we are able to compare
two axioms structurally, we have not yet considered
the semantic mapping between axioms. Another way
to categorize the tools is to consider the type of in-
put on which the tool relies in its analysis and which
it requires: (1) class names or natural-language defi-
nitions, (2) class hierarchy and properties, or (3) in-
stances. Our approach is based on (2) and (4); we
also introduces a new type of input: Axioms (includ-
ing Schemata Axioms and Domain Axioms).
Then, in (Ehrig and Sure, 2004), a similarity stack
is provided in order to classify the different measures
that can be used to perform ontology matching. This
stack is composed of five levels: the Entities level,
the Semantic Nets level, the Description Logics level,
the Restrictions level and the Rules level. For the first
three levels, the authors provide similarity measures
which of course differ according to semantic com-
plexity of the level which is considered. However, for
the Restrictions level and Rules level, no measure is
proposed. Explanations given by the authors are the
following: ”the features like algebraic properties or
equivalence/disjointness are not sufficiently used by
the community to be considered as a material for sim-
ilarity measure; for the Rules level, there has not been
sufficient research and practical support for the Rule
Layer of the Semantic Web Layer Cake”. Our work
must be considered as an extension of this classifica-
tion in the sense that it provides measures based on
the axioms of the domain which include both the Re-
strictions level and the Rules level. However, as we
claim that it is not possible to consider rules and con-
straints at the ontological level (rules and constraints
only exist at the operational level, we propose to mod-
ify the stack by merging the two levels Restrictions
and Rules into only one: the Axioms level.
5 CONCLUSION
In this paper, we have introduced a new ontology
matching approach. This approach, which mainly re-
lies on graph-based representations and graph-based
reasoning mechanisms, is particularly relevant to
manage heavyweight ontologies since the main com-
ponents of these ontologies are axioms which can
be easily represented and compared with graph-based
solutions. Our method has the advantage of incor-
porating most of the descriptive features of a heavy-
weight ontology into the matching process whereas
most of the current methods cover only subsets of a
lightweight ontology (mainly the hierarchy of con-
cepts and their natural language expression). Of
course, this method, although applicable, is not very
efficient in a context of lightweight ontologies (and
this is why we are not yet involved in the OAEI cam-
paigns) . However, as demonstrated by the current
challenge ”Reasoning the Semantic Web”, the need
for developing heavyweight ontologies inevitably will
increase in an immediate future. So, it seems interest-
ing to focus on developing matching techniques dedi-
cated to this type of ontology.
REFERENCES
Ashpole, B., Ehrig, M., Euzenat, J., and Stuckenschmidt,
H. (2005). Ontology alignment evaluation initiative -
2005. In Proceedings of the K-CAP 2005 Workshop on
Integrating Ontologies. CEUR Proceedings - Volume
156.
Benjamins, R., Euzenat, J., Noy, N., Shvaiko, P., Stuck-
enschmidt, H., and Uschold, M. (2006). Ontology
alignment evaluation initiative - 2006. In Proceedings
of the International Workshop on Ontology Matching,
http://oaei.ontologymatching.org/2006/.
Berners-Lee, T., Handler, J., and Lassila, O. (2001). The
semantic web. In Scientific American, volume 248,
pages 35–43.
Doan, A. and Halevy, A. (2005). Semantic integration re-
search in the database community: A brief survey. In
AI Magazine, Special Issue on Semantic Integration.
Ehrig, M. and Sure, Y. (2004). Ontology Mapping - an inte-
grated approach. In Proceedings of the First European
Semantic Web Symposium, pages 76–91. Springer-
Verlag (LNCS 3053).
F
¨
urst, F., Lecl
`
ere, M., and Trichet, F. (2004). Operational-
izing domain ontologies: a method and a tool. In
de Mantaras, R. L. and Saitta, L., editors, European
Conference on Artificial Intelligence (ECAI’2004),
pages 318–322. IOS Press.
F
¨
urst, F. and Trichet, F. (2005a). Integrating domain on-
tologies into KBS. In 18th International Florida
Artificial Intelligence Research Society Conference
(FLAIRS’2005), pages 826–827. AAAI Press.
F
¨
urst, F. and Trichet, F. (2005b). Toocom: bridge the
gap between ontologies and knowledge-based sys-
tems. In 17th International Conference on Knowledge
Engineering and Software Engineering (SEKE’2005),
pages 235–243. KSI editors.
Gomez-Perez, A., Fernandez-Lopez, M., and Corcho, O.
(2003). Ontological Engineering. Springer, Advanced
Information and Knowledge Processing.
Noy, N. F. (2004). Semantic integration: A survey
of ontology-based approaches. SIGMOD Record,
33(4):65–70.
Shvaiko, P. and Euzenat, J. (2005). A survey of schema-
based matching approaches. In Journal on Data Se-
mantics (3730), pages 76–171. Springer-Verlag.
Sowa, J. (1984). Conceptual Structures : information pro-
cessing in mind and machine. Addison-Wesley.
ICEIS 2007 - International Conference on Enterprise Information Systems
270