IMPLEMENTING PRIORITIZED REASONING IN LOGIC
PROGRAMMING
Luciano Caroprese, Irina Trubitsyna and Ester Zumpano
DEIS, University of Calabria, 87030 Rende, Italy
Keywords:
Answer Set Optimization, Choice Optimization, Prioritized Logic Programming.
Abstract:
Prioritized reasoning is an important extension of logic programming and is a powerful tool for expressing
desiderata on the program solutions in order to establish the best ones. This paper discusses the implemen-
tation of the case of preference relation among atoms and introduces a system, called CHOPPER, reali-
zing choice optimization recently proposed in (Caroprese et al., 2007). CHOPPER supports the ASO
Ch
and
ASO
FCh
semantics based on the concept of “choice”, as a set of preference rules describing common choice
options in different contexts, and the ASO semantics (Brewka et al., 2003), which valuates each preference
rule separately. This paper outlines the architecture of the system, discusses aspects of the choice identification
strategies and of the feasibility of choice options. Moreover, the comparison of the proposed approach with
the other implementation approaches proposed in the literature is provided.
1 INTRODUCTION
Prioritized reasoning is an important extension of
logic programming, used in a large variety of AI prob-
lems. The most common form of preference con-
sists in specifying preference conditions among rules
(Brewka and Eiter, 1999; Delgrande et al., 2000; Del-
grande et al., 2003; Gelfond and Son, 1997), whereas,
some other proposals admit the expression of prefe-
rence relations among atoms (Brewka et al., 2003;
Sakama and Inoue, 2000; Wakaki et al., 2003). See
(Delgrande et al., 2004) for a survey on this topic.
This work is a contribution to realizing prioritized rea-
soning in logic programming in the presence of prefe-
rence conditions involving atoms. This topic has been
investigated in (Brewka et al., 2003) and (Sakama and
Inoue, 2000), proposing the ASO and PLP semantics
respectively. The ASO semantics evaluates the degree
of satisfaction of all preference rules to determine the
preferred models and can establish a preference re-
lation between each couple of models directly. On
the contrary, the PLP semantics compares two mo-
dels only on the basis of their common preferences,
and needs to test the transitive property to derive the
non directly visible preference relations; this lies in
a more complex implementation. A generalization of
the ASO semantics which look beyond the each sin-
gle preference rule, by considering preferences as a
tool for choice representation, was recently proposed
in (Caroprese et al., 2007).
The prioritized reasoning based on the choice optimi-
zation is illustrated by the following example.
Example 1 Consider the prioritized program
h
P
1
, Φ
1
i. P
1
describes the possible menus by means
of three rules r
1
, r
2
and r
3
, where ⊕ states that
exactly one of the head’s atoms has to be taken in the
model, and three constraints c
1
, c
2
and c
3
, i.e. rules
with empty heads satisfied if the body is false (e.g.
c
1
states that bee f and red cannot be simultaneously
present).
r
1
: fish ⊕ beef ← c
1
: ← beef, red
r
2
: red ⊕ white ← c
2
: ← beef, pie
r
3
: pie ⊕ ice-cream ← c
3
: ← fish, white
ρ
1
: white > red ← fish
ρ
2
: red > white ← beef
ρ
3
: pie > ice-cream ←
P
1
has three stable models M
1
= {fish, red, pie},
M
2
= {fish, red, ice-cream} and M
3
= {beef,
white, ice-cream}. The preference rules ρ
1
and ρ
2
specify that (i) the choice of drink (white or red) fol-
lows the selection of the main dish (fish or bee f);
94
Caroprese L., Trubitsyna I. and Zumpano E. (2007).
IMPLEMENTING PRIORITIZED REASONING IN LOGIC PROGRAMMING.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 94-100
DOI: 10.5220/0002353800940100
Copyright
c
 SciTePress

(ii) white is better than red in the presence of fish;
(iii) red is better than white in the presence of bee f;
whereas ρ
3
denotes that pie is better than ice-cream.
M
1
is better than M
2
as pie is preferred to ice-cream
and they have the same choice option of drink. M
1
is better than M
3
as they have the second best choice
of the drink (in the presence of fish and beef respec-
tively), whereas the choice of the dessert is satisfied
better by M
1
. Thus M
1
is a preferred model.
Observe that the ASO semantics, which considers
each preference rule separately, cannot establish the
preference ordering between M
1
and M
3
and derives
that both M
1
and M
3
are preferred models. In more
details, it derives that M
1
is better that M
3
w.r.t. ρ
2
and M
3
is better that M
1
w.r.t. ρ
1
, thus they cannot be
compared. 
This paper discusses the implementation of choice op-
timization in logic programming and presents a sy-
stem, called CHOPPER, realizing this kind of priori-
tized reasoning.
2 PRELIMINARIES
An Answer Set Optimization program, ASO, is a pair
h
P , Φi, where P is called Generating Program and Φ
is called Preference Program; Φ consists of a finite
set of rules of the form C
1
> ··· > C
k
← body, where
body is a conjunction of literals, i.e. atoms or negation
of atoms, andC
i
s are boolean combinations of literals.
Intuitively, a preference rule ρ ∈ Φ above described
introduces a preference order among C
1
, ...,C
k
: C
i
is
preferred toC
j
, for i < j and i, j ∈ [1..k]. Thus, the set
of preferences Φ determines a preference ordering on
the answer sets described by
P .
Let Φ = {r
1
, ..., r
n
} be a preference program and S
be an answer set, then S induces a satisfaction vector
V
s
= [v
s
(r
1
), ..., v
s
(r
n
)] where: a) v
s
(r
j
) = I, if r
j
is Ir-
relevant to S, i.e. (i) the body of r
j
is not satisfied in S
or (ii) the body of r
j
is satisfied, but none of the C
i
s is
satisfied in S. b) v
s
(r
j
) = min{i | S |= C
i
}, otherwise.
The satisfaction vectors are used to compare the ans-
wer sets under the assumption that I is equal to 1 (i.e.,
v
S
j
(r
i
) = I is equivalent to v
S
j
(r
i
) = 1).
Let S
1
and S
2
be two answer sets, then (i) S
1
≥ S
2
if
V
S
1
≤ V
S
2
, i.e. if v
S
1
(r
i
) ≤ v
S
2
(r
i
) for every i ∈ [1..n];
(ii) S
1
> S
2
if V
S
1
< V
S
2
, i.e. if V
S
1
≤ V
S
2
and for some
i ∈ [1..n] v
S
1
(r
i
) < v
S
2
(r
i
).
A set of literals S is an preferred (optimal) model of
an ASO program h
P , Φi if S is an answer set of P and
there is no answer set S
′
of
P such then S
′
> S.
Given an ASO program h
P , Φi, its computational
complexity is one level above the complexity of the
generating program P (Brewka et al., 2003).
ASO
Ch
Semantics. The generalization of ASO se-
mantics, which captures the intuition depicted in the
Example 1, is called the ASO
Ch
semantics. Diffe-
rently from the ASO semantics, the ASO
Ch
seman-
tics looks beyond the single preference rules, consi-
dering them as a tool for choice representation: head
atoms correspond to the choice options, whereas the
body of preference rule specifies the choice context,
i.e. the decisions which have to precede this choice.
The ASO
Ch
semantics admits only atoms or disjunc-
tion of atoms in the head of preference rules. If C
i
is a
disjunction of atoms, all atoms in C
i
are equally good
choice options; atoms in C
i
are preferred to the atoms
in C
j
, for i < j and i, j ∈ [1..k]. The evaluation stra-
tegy consists in the identification of choices and in the
comparison of choices instead of single rules in order
to select preferred models.
More specifically, the partition of Φ into a set of
choices (subset of preference rules), denoted by
Ch(Φ), is performed following the choice identifica-
tion strategy: two preference rules ρ
1
and ρ
2
define
the same choice Ch, denoted by ρ
1
, ρ
2
∈ Ch, if (i) ρ
1
and ρ
2
have at least one common atom in their heads;
and (ii) ∃ρ
3
such that ρ
1
, ρ
3
∈ Ch and ρ
3
, ρ
2
∈ Ch.
The ASO
Ch
semantics presumes that prioritized pro-
grams are well-formed, i.e. each set of preference
rules ρ
1
, ..., ρ
k
defining a choice is specified over al-
ternative contexts. This hypothesis ensures that in
each model M at most one of the different contexts
of a choice is satisfied, i.e. ∀ model M, ∀ Ch, there is
at most one preference rule ρ ∈ Ch, denoted as active
in M, such that body(ρ) is satisfied in M.
After constructing the set of choices Ch(Φ), the pre-
ferred stable models of h
P , Φi are computed by as-
sociating to each model M of
P a satisfaction vec-
tor reporting the degree of satisfaction of each choice
Ch∈ Φ. The evaluation strategy of ASO
Ch
semantics
is illustrated by the following example.
Example 2 Consider the prioritized program
h
P
1
, Φ
1
i reported in Example 1. The preference
rules {ρ
1
, ρ
2
} ∈ Φ
1
, having common atoms in their
heads, define the same choice, say Ch
dr
, whereas
the last preference rule ρ
3
defines another choice,
say Ch
d
. Consequently, the set of preference rules
{ρ
1
, ρ
2
, ρ
3
} ∈ Φ
1
is partitioned into two different
choices: Ch
dr
= {ρ
1
, ρ
2
} and Ch
d
={ρ
3
} that models
the choice of drink and dessert respectively. The
choice satisfaction vectors are V
M
1
= [2, 1], V
M
2
= [2, 2],
V
M
3
= [2, 2], consequently, M
1
is the preferred model
owing to the dessert choice. Note that ASO semantics
gives V
M
1
= [2, I, 1], V
M
2
= [2, I, 2], V
M
3
= [I, 2, 2] and
returns M
1
and M
3
as preferred models. It does
not admit the comparison of M
1
and M
3
owing to
opposite satisfaction degrees of ρ
1
and ρ
2
. 
IMPLEMENTING PRIORITIZED REASONING IN LOGIC PROGRAMMING
95

Given a prioritized program hP , Φi, the ASO
Ch
se-
mantics coincides with the ASO semantics if
6∃ρ
1
, ρ
2
∈ Φ having at least one common atom in their
heads.
The computational complexity of ASO
Ch
semantics is
not increased w.r.t. the ASO semantics. In fact, the
choice identification can be done in polynomial time;
while given a model M the evaluation of its choice
satisfaction vector V
M
can be performed by (i) iden-
tifying the active rule for each choice, which can be
done in polynomial time; and (ii) establishing the sa-
tisfaction degrees of the active rules as in the case of
ASO semantics.
ASO
FCh
Semantics. Given a choice Ch and a mo-
del M, the ASO
Ch
semantics evaluates M on the ba-
sis of the selected option in the active preference rule
ρ ∈ Ch. Observe that the head atoms of ρ describe
the possible options of Ch and the preference among
them, without taken into account their feasibility, i.e.
the really possibility of selecting these options du-
ring the choice. This property depends on the con-
straints present in logic program and is determined by
the choice context in a given model, i.e. by the set of
atoms whose selection precede this choice. An alter-
native to the ASO
Ch
semantics evaluating the choices
on the basis on their really possible options is called
ASO
FCh
semantics.
Example 3 Consider the prioritized program
h
P
3
, Φ
3
i, describing different menus and the
preferences among drinks and desserts:
r
1
: fish ⊕ beef ← c
1
: ← beef, pie
r
2
: red ⊕ white ⊕ beer ← c
2
: ← fish, ice-cream
r
3
: pie ⊕ ice-cream ←
ρ
1
: white > red > beer ← fish
ρ
2
: red ∨ beer > white ← beef
ρ
3
: pie > ice-cream ← beer
The generating program
P
3
has six stable models:
M
1
= {fish, white, pie}, M
2
= {fish, red, pie},
M
3
= {fish, beer, pie}, M
4
= {beef, white, ice-
cream}, M
5
= {beef,red, ice-cream} and M
6
=
{beef, beer, ice-cream}. Φ
3
defines the set of
choices Ch = {Ch
dr
, Ch
d
}, where Ch
dr
= {ρ
1
, ρ
2
} and
Ch
d
={ρ
3
} describe the choices of drinks and desserts
respectively.
In order to establish the set of preferred solutions
the ASO
Ch
semantics constructs the choice satisfac-
tion vector for each model: V
M
1
= [1, I ], V
M
2
= [2, I ],
V
M
3
= [3, 1], V
M
4
= [2, I ], V
M
5
= [1, I ], V
M
6
= [1, 2] and
obtain M
1
and M
5
as a result. The ASO
FCh
semantics
takes into account the feasibility of choice options and
substitutesV
M
6
= [1, 2] byV
′
M
6
= [1, 1] following the in-
tuition that its option of the dessert choice (ice-cream)
is the unique (and, consequently, best) possible op-
tion. Thus M
6
is also a preferred model. 
The implementation of the ASO
FCh
semantics re-
quires the test of the feasibility of choice options,
which can be performed in a polynomial time. Thus,
the computational complexity of ASO
FCh
semantics is
not increased w.r.t. the ASO
Ch
semantics (Caroprese
et al., 2007).
3 THE CHOPPER SYSTEM
CHOPPER (CHoice OPtimizer for PrioritizEd
Reasoning) is an answer set optimization system rea-
lizing prioritized reasoning based on the choice eva-
luation.
The system prototype has been developed on top
of the well-known DLV prover (Leone et al., 2002)
by using Java 2 Platform. In particular, the ans-
wer set evaluation is performed with the DLV sy-
stem, whereas the prioritized reasoning and the user
interface are realized by means of personalized java
procedures. We point out that besides DVL several
other deductive systems based on stable model se-
mantics have been proposed in the literature (Smod-
els, DeRes) (Cholewinski et al., 1996; Syrjanen and
Niemela, 2001). The choice of DLV is orthogonal
w.r.t. the development of the prototype, since CHOP-
PER can exploit any other deductive systems propo-
sed in the literature.
Using of CHOPPER. CHOPPER receives in in-
put the prioritized program and the specification of
the semantics to be applied and extracts and returns
the preferred stable models as a result. The system
can be used by means of a User Interface -
UI - which
allows to specify (i) the prioritized program - h
P , Φi,
(ii) the semantics -
C S - chosen among the semantics
discussed in the paper and allows to visualize the ob-
tained result, i.e. the set of preferred stable models -
P S M .
The running of CHOPPER for the program h
P
3
, Φ
3
i
under the ASO
FCh
semantics is provided in Figure 1.
In more details, the prioritized program is provided
to the system by means of two different textual files,
written following the DLV syntax, containing the ge-
nerating program and the preference program, respec-
tively. Note that in the preference program the system
admits the symbol “>” for expressing the preference
order among choice options.
CHOPPER also offers the possibility of comparing
two different semantics by evidencing the set of mo-
dels common to both the semantics. The result of
comparison of ASO
Ch
and ASO
FCh
for the program
h
P
3
, Φ
3
i is provided in Figure 2. The symbol “∗”
ICEIS 2007 - International Conference on Enterprise Information Systems
96

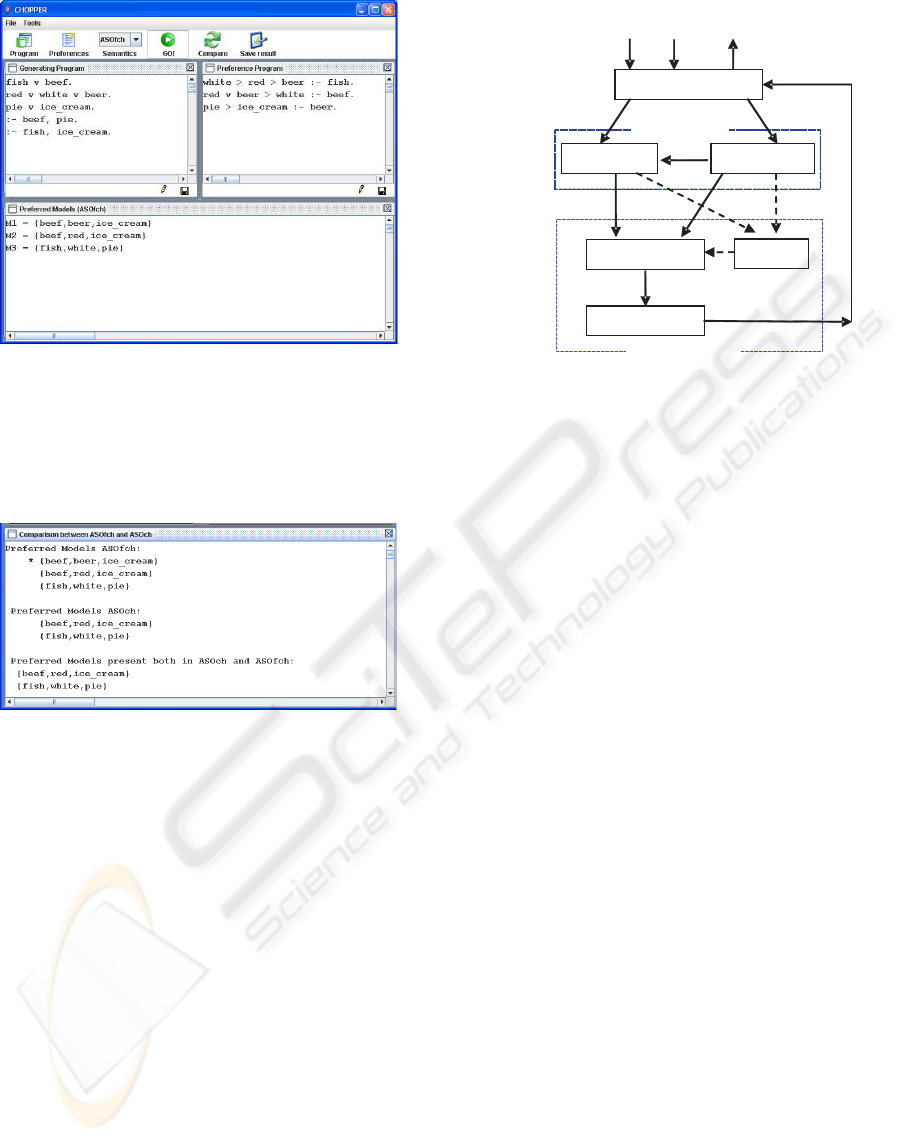
Figure 1: The U I of CHOPPER.
marks the first model provided by the ASO
FCh
seman-
tics and states that this model is not provided by the
ASO
Ch
semantics.
Figure 2: Comparison result.
CHOPPER Architecture. The overall architec-
ture of the CHOPPER prototype is reported in Fi-
gure 3. The core of the system consists in two main
blocks: the Analyzer Block and the Evaluator Block
described below.
The Analyzer Block is constituted by two different
modules: the
P − analyzer and the Φ − analyzer.
• The Φ-analyzer takes in input the set of prefe-
rence rules Φ and the chosen semantics C S , and
computes Ch(Φ), i.e. the partition of Φ into the
set of choices by following the choice identifica-
tion strategy.
• The
P -analyzer receives in input the generating
program
P and additional information gained
from Φ-analyzer, and invokes the DLV prover
(Leone et al., 2002) in order to obtain the stable
models of the program
P , S M (P ).
• As an additional task, in the case of the ASO
FCh
"MÎSM(P), V
M
F-tester
V-constructor
Examiner
P
Ö,CS
SM(P)
Ch(Ö), CS G(Ö)
AuxRules
PSM
Analyzer Block
Evaluator Block
User Interface
P-analyzer
< P, Ö >
PSM
Ö-analyzer
CS
IC(P)
Figure 3: The architecture of CHOPPER.
semantics, the Φ-analyzer establishes the prece-
dence relation among choices, while the
P -
analyzer extracts the set of constraints of
P ,
IC(
P ), necessary for testing the feasibility of
choice options.
The Evaluator Block is responsible for P S M discove-
ring and is constituted by three modules: the F-tester,
the V-constructor and the Examiner.
• The F-tester is able to test the feasibility of choice
options.
• The V-constructor receives in input S M (P ), C S
and Ch(Φ), and constructs the (feasible) choice
satisfaction vector V
M
for each stable model M ∈
SM (P ).
• The Examiner module, performs the comparison
of the choice satisfaction vectors so that establish-
ing the set of preferred stable models P S M . The
result is provided to the
UI responsible of user’s
communication.
4 IMPLEMENTATION
In the following we detail the implementation of the
main modules constituting the Analyzer Block and the
Evaluator Block.
4.1 Φ-analyzer
The Φ-analyzer examines the structure of preference
rules in order to establish the partition of Φ into the set
of choices Ch(Φ) and to determine the order among
choices. Moreover, it produces the set of auxiliary
IMPLEMENTING PRIORITIZED REASONING IN LOGIC PROGRAMMING
97

rules necessary to simplify the construction of the
choice satisfaction vector without increasing the com-
putational complexity of
P .
Choice identification. The choice identification
process performed by the Φ − analyzer depends on
the selected semantics and is based on the choice
identification strategy. In the case of ASO semantics
each rule is associated with a different choice. In the
case of ASO
Ch
or ASO
FCh
semantics the rules, having
at least one common atom in their heads, are assigned
to the same choice. The algorithm, performing this
task, is presented in Figure 4. It takes in input a set of
preference rules Φ and returns the partition of Φ into
the set of choices Ch(Φ).
Algorithm 1 Choice Identification
Input: A set of preference rules: Φ;
Output: A set of choices: Ch(Φ);
begin
Ch(Φ) = {};
while (Φ is not empty) {
ρ = extractFirstElement(Φ);
Ch = {ρ}; Φ = Φ− {ρ};
update=true;
while (update==true ) {
update=false;
for each ρ
′
∈ Φ
for each ρ ∈ Ch
if (sameChoice(ρ, ρ
′
)) {
Φ = Φ − {ρ
′
};Ch = Ch + {ρ
′
};
update = true; }
} Ch(Φ) =Ch(Φ)+Ch;
} return Ch(Φ);
end.
Figure 4: Choice Identification Algorithm.
At each step of the external iteration process the al-
gorithm selects the first preference rule ρ from Φ
and identifies and extracts all preference rules from Φ
defining the same choice of ρ, called Ch. The function
sameChoice receives in input two preference rules ρ
and ρ
′
and returns true if they have at least one com-
mon atom in their heads. In the positive case, ρ
′
is
added to Ch. The transitive property is supported by
the nested while-block, which ensures that all prefe-
rence rules defining the same choice are considered
together. For the sake of simplicity of presentation,
the optimization details, regarding the implementa-
tion of the transitive property are not reported in the
above algorithm.
Choice ordering. The relationship among choices
can be established by means of the Choice depen-
dency graph described below.
Definition 1 Choice dependency graph: Given a
set of choices Φ = {Ch
1
, ..., Ch
n
}, its dependency
graph G(Φ) is an oriented graph hN, Ei, where N
denotes the set of nodes associated to choices, i.e
N = {Ch
1
, ..., Ch
n
}, and E denotes the set of edges,
E = {e(Ch
i
, Ch
j
)|∃ρ
2
∈ Ch
j
,ρ
1
∈ Ch
i
and ∃ atom A,
s.t. A ∈ body(ρ
2
) ∧ A ∈ head(ρ
1
)}. 
The implementation of G(Φ) is really simple as its
nodes correspond to the choices, whereas the pre-
sence of the edge e(Ch
i
, Ch
j
) can be tested by consi-
dering the choice options of Ch
i
and the positive body
atoms, present in each ρ ∈ Ch
j
.
Definition 2 Given a set of choices Φ = {Ch
1
, ...,
Ch
n
} and its dependency graph G(Φ), we say that the
choice Ch
i
precedes Ch
j
, denoted by Ch
i
≺ Ch
j
, if
there is a path from the vertex Ch
i
to the vertex Ch
j
,
whereas there is no path from Ch
j
to Ch
i
. 
Previous definition allows the computation of the set
of choices precedent to a choice Ch: Ch
′
precedes Ch
if there is a path from the vertex Ch
′
to the vertex Ch;
moreover, it takes into account the intuition that we
cannot establish a precedence relation between two
choices if they are involved in a cycle.
Figure 5: Choice Dependency Graph.
Example 4 Consider the Choice dependency graph
presented in Figure 5. There are two nodes Ch
2
and Ch
3
involved in a cycle, thus we cannot estab-
lish the precedence relation between the correspon-
ding choices. On the other hand, we can deduce, that
Ch
1
≺ Ch
2
, Ch
1
≺ Ch
3
, Ch
1
≺ Ch
4
, Ch
2
≺ Ch
4
and
Ch
3
≺ Ch
4
. 
4.2 V-constructor and F-tester
The V-constructor and the F-tester modules collabo-
rate in order to construct the choice satisfaction vector
for each stable model of the generating program.
Choice Satisfaction Vector. The V-constructor re-
ceives in input
SM (P ), C S and Ch(Φ), and con-
structs the choice satisfaction vector V
M
for each sta-
ICEIS 2007 - International Conference on Enterprise Information Systems
98

ble model M ∈ SM (P ) following the chosen seman-
tics
C S . More specifically, given a model M, V
M
=
[(v(Ch
1
), ..., v(Ch
n
)] reports the satisfaction degree of
each choice Ch
i
∈ Ch(Φ).
In the case of ASO
Ch
semantics each choice Ch
i
is de-
scribed by the set of preference rules, but at most one
of them is active in M and v(Ch
i
) reports its satis-
faction degree. The cases than (i) no preference rule
is active in M or (ii) there exists an active rule, but
no choice option described by it is present in M, are
considered as the best cases, i.e. v(Ch
i
) = 1.
In the case of the ASO semantics each choice is de-
scribed by a unique preference rule, thus V
M
coin-
cides with the satisfaction vector proposed in (Brewka
et al., 2003).
If the ASO
FCh
is chosen, V
M
has to be constructed by
taking into account the feasibility of choice options.
Consider, for instance, the choice Ch
i
and suppose
the choice option d-th to be present in M, whereas
k options preceding it are not feasible in M, then
v(Ch
i
) = d −k. The V-Constructor performs this task
by interacting with the F-tester module, able to ana-
lyze the feasibility of choice options.
Feasibility Testing. The F-tester module is in
charge of verifying the feasibility of the choice op-
tions present in a preference rules. The goodness of a
model depends on the degree of satisfaction of a set of
preference rules; anyhow, the measure of the degree
of satisfaction of a preference rule, say ρ, active w.r.t.
a model M should be evaluated by only considering
the set of choice options feasible in M. In order to
better depict this intuition, let’s examine the program
h
P
3
, Φ
3
i and the model M
6
reported in Example 3. ρ
3
is active in M
6
and as the choice of pie is not feasible
in M
6
, ice-cream becomes the best choice option as it
is the only feasible one.
In order to capture this behavior the F-tester module
computes the context of a choice Ch in a model M as
the subset of atoms in M whose selection precedes Ch.
Intuitively, this subset of atoms can be individuated (i)
by analyzing the choice dependency graph in order
to establish the set of choices preceding Ch, (ii) by
identifying the atoms selected during these choices,
or whose selection precede these choices.
More formally, given a set of choices Ch(Φ), the con-
text of a choice Ch w.r.t. a model M, denoted by
cntx
M
(Ch), is the conjunction
ρ
′
∈Ω(Ch,M)
(body(ρ
′
) ∧
best
head(ρ
′
)) body(ρ), where Ω(Ch, M) = {ρ
′
| ∃ Ch
′
∈
Φ s.t. Ch
′
≺ Ch ∧ ρ
′
∈ Ch
′
∧ M |= body(ρ
′
)} , ρ ∈ Ch is s.t.
M |= body(ρ) and best head(ρ
′
) is the best choice option
of ρ
′
belonging to M.
Example 5 Consider the prioritized program
h
P
3
, Φ
3
i from the Example 3. Notice that beer is
the option of the drink choice and that each model
M containing beer performs this choice following
either the preference rule ρ
1
or ρ
2
, i.e. before beer,
M has selected either fish or beef. Let’s consider the
model M
6
: ρ
3
is active in M
6
as it contains beer, and
beer follows the selection of beef. Thus the choice
described by ρ
3
works in the presence (context) of
{beef, beer}. 
Given a model M and a choice Ch, the module is
therefore in charge of testing the feasibility of the op-
tions expressed in Ch by considering the constraints
of the generating program and the context of Ch in M.
Definition 3 Feasibility of choice options: Given a
prioritized program h
P , Φi defining the set of choices,
a stable model M of
P , a choice Ch ∈ Ch(Φ) and a
preference rule ρ ∈ Ch, then A
i
∈ head(ρ) is a feasible
choice option w.r.t. M iff A
i
∧cntx
M
(Ch) |= IC(
P ) and
is unfeasible otherwise. 
The test of the feasibility is performed by the F-tester
module by constructing for each tested choice option
a logic program which is satisfied if the tested option
is feasible and fails otherwise. This program contains
(i) the atoms of the choice context and a tested atom
(choice option) as facts and (ii) the set of constraint
IC(
P ) of the generating program P . The F-tester in-
vokes the DLV prover in order to solve this program
and if the program does not have stable models de-
duces that the tested option is unfeasible, or deduces
that it is feasible otherwise.
5 OTHER APPROACHES
The computation of preferred models proposed in
(Brewka et al., 2003) and (Wakaki et al., 2003) for
ASO semantics and PLP semantics respectively is
based on the use of a tester program
1
. In more de-
tails, given a prioritized logic program h
P , Φi, the
tester program takes in input a candidate solution S
of P and looks for the other solutions of P (strictly)
preferred w.r.t. S. This latter task is performed by
generating the solutions of
P and by comparing them
with S.
The ASO semantics permits a direct comparison of
two solutions, thus the tester program can be used as
follows. The computation starts with an arbitrary so-
lution S of
P . If the tester fails, S is an optimal solu-
tion and the computational process stops. Otherwise,
a strictly better solution S
1
is discovered and the tester
1
A similar technique was also implemented in (Jan-
hunen et al., 2000; Brewka, 2002; Sakama and Inoue,
2000).
IMPLEMENTING PRIORITIZED REASONING IN LOGIC PROGRAMMING
99

is run with S
1
as input. This process continues until
an optimal solution is reached.
On the contrary,
P L P semantics introduces the tran-
sitive property of preference relation, thus admits the
preference relation between two solutions which are
not directly comparable. Consequently, in this case
two-step procedure is needed: in the first step all
the direct preference relations among solutions have
to be established; then the transitive relations can be
discovered and the final conclusion can be derived.
Wakaki et. al in (Wakaki et al., 2003) implement the
direct comparisons by testing each answer set of
P
with a tester program; and then create an auxiliary
logic program which extracts all preferred solutions
on the basis of the preference relations generated at
the previous step and those discovered by using the
transitive property.
In the general case, both the approaches, previously
described, need to perform more calls to the tester
program which is in charge of computing the set of
solution of
P . The approach adopted in CHOPPER
aims to avoid the redundant computation of the set of
solution of
P , performed during each call to the tester
program. CHOPPER uses once the logic prover to
find the set of solutions of the problem, and realizes
the prioritized reasoning by means of personalized
comparison procedures.
6 CONCLUSION
In this paper the implementation of prioritized rea-
soning in logic programming has been discussed.
In particular, the case of preference relation among
atoms has been investigated and a system, called
CHOPPER, has been described. This system realizes
choice optimization in logic programming by imple-
menting the ASO
Ch
and ASO
FCh
semantics recently
proposed in (Caroprese et al., 2007), and supports the
ASO semantics (Brewka et al., 2003). In this paper
the architecture of the system has been presented and
aspects of the choice identification strategies and of
the feasibility of choice options has been discussed.
Moreover, the comparison of the proposed approach
with the other implementation approaches proposed
in the literature has been provided.
REFERENCES
Brewka, G. (2002). Logic programming with ordered dis-
junction. In Proc. of the 18th Nat. Conf. on Artifi-
cial Intelligence (AAAI/IAAA), pages 100–105. AAAI
Press.
Brewka, G. and Eiter, T. (1999). Preferred answer sets
for extended logic programs. Artificial Intelligence,
109(1-2):297–356.
Brewka, G., Niemela, I., and Truszczynski, M. (2003). Ans-
wer set optimization. In Proc. of the 18th Int. Joint
Conf. on Artificial Intelligence, pages 867–872. Mor-
gan Kaufmann.
Caroprese, L., Trubitsyna, I., and Zumpano, E. (2007).
A framework for prioritized reasoning based on the
choice evaluation. In Proc. of the 22nd Annual ACM
Symposium on Applied Computing.
Cholewinski, P., Marek, V. W., and Truszczynski, M.
(1996). Default reasoning system deres. In Proc.
of the 5th Int. Conf. KR’97, pages 518–528. Morgan
Kaufmann.
Delgrande, J. P., Schaub, T., and Tompits, H. (2000). Logic
programs with compiled preferences. In Proc. of the
14th Eur. Conf. on Artificial Intelligence, pages 464–
468. IOS Press.
Delgrande, J. P., Schaub, T., and Tompits, H. (2003). A
framework for compiling preferences in logic pro-
grams. TPLP, 3(2):129–187.
Delgrande, J. P., Schaub, T., Tompits, H., and K., W. (2004).
A classification and survey of preference handling ap-
proaches in nonmonotonic reasoning. Computational
Intelligence, 20(2):308–334.
Gelfond, M. and Son, T. (1997). Reasoning with prioritized
defaults. In Proc. of the 3d Int. Workshop LPKR’97,
pages 164–223. Springer.
Janhunen, T., Niemela, I., Simons, P., and You, J.-H. (2000).
Unfolding partiality and disjunctions in stable model
semantics. In Proc. of the 7th Int. Conf. KR’00, pages
411–419. Morgan Kaufmann.
Leone, N., Pfeifer, G., Faber, W., Calimeri, F., Dell’Armi,
T., Eiter, T., Gottlob, G., Ianni, G., Ielpa, G., Koch,
K., Perri, S., and Polleres, A. (2002). The dlv sy-
stem. In Proc. of Eur. Conf. JELIA’02, pages 537–540.
Springer.
Sakama, C. and Inoue, K. (2000). Priorized logic program-
ming and its application to commonsense reasoning.
Artificial Intelligence, 123:185–222.
Syrjanen, T. and Niemela, I. (2001). The smodels system.
In Proc. of the 6th Int. Conf. LPNMR’01, pages 434–
438. Springer.
Wakaki, T., Inoue, K. nd Sakama, C., and Nitta, K. (2003).
Computing preferred answer sets in answer set prog-
ramming. In Proc. of the 10th Int. Conf. LPAR’03,
pages 259–273. Springer.
ICEIS 2007 - International Conference on Enterprise Information Systems
100