AN EMPIRICAL STUDY OF SIGNIFICANT VARIABLES

FOR TRADING STRATEGIES

M. Delgado Calvo-Flores, J. F. Núñez Negrillo

Departamento de Ciencias de la Computación e Inteligencia Artificial. E.T.S. de Ingeniería Informática

Universidad de Granada, 18071 Granada, Spain

E. Gibaja Galindo

Departamento de Informática y Análisis Numérico, Campus de Rabanales, Edificio Albert Einstein

Universidad de Córdoba, 14071 Córdoba, Spain

C. Molina Férnandez

Departamento de Informática, Campus las Lagunillas, Edificio A3 (Ingeniería y Tecnología)

Universidad de Jaén, 23071 Jaén, Spain

Keywords: Significant variables, genetic algorithms, stock market.

Abstract: Nowadays, stock market investment is governed by investment strategies. An investment strategy consists

in following a fixed philosophy over a period of time, and it can have a scientific, statistical or merely

heuristic base. No method currently exists which is capable of measuring how good an investment strategy

is either objectively or realistically. Through the use of Artificial Intelligence and Data Mining tools we

have studied the different investment strategies of an important Spanish management agency and extracted a

series of significant characteristics to describe them. Our objective is to evaluate and compare investment

strategies in order to be able to use those which produce a peak return in our investment.

1 INTRODUCTION

Stock market trading is one of the most popular

forms of investment both on a corporate and

individual level. Despite the vast number of studies

which exist (Baba, 2002; Chapman, 1994; Liu,

1997; Skabar, 2001), the “stock exchange world” is

so complex that there is still no universally accepted

method for optimizing purchase management in

terms of profits. We are faced with a very complex,

and at times chaotic and unpredictable problem and

one which also has a number of restrictions common

to the real world (capital available, maximum share

volume, liquidity, etc.) which make it yet more

difficult.

The objective of this work is to establish a

procedure based on significant variables in order to

characterise the results of a strategy’s behaviour

according to a series of performance measures.

1.1 Stock Market Indexes

A stock market index corresponds to a statistical

compound, usually a number, which attempts to

reflect variations in the average value or profitability

of the shares comprising it. Generally speaking, the

shares which comprise the index have common

characteristics: they belong to the same stock

market, they have a similar stock market

capitalization, or they belong to the same industry.

These are usually used as the reference point for

different portfolios, such as mutual funds.

The oldest index is the Dow Jones Industrial

Average or the Dow Jones in short. This index was

created to measure economic activity in the United

States of America. It currently comprises 30

companies.

There are also other indexes throughout the

world, and examples of these are the Ibex 35 in

Spain, NIKKEI 225 in Japan, FTSE 100 in Great

Britain, and CAC 40 in France.

330

Delgado Calvo-Flores M., F. Núñez Negrillo J., Gibaja Galindo E. and Molina Férnandez C. (2007).

AN EMPIRICAL STUDY OF SIGNIFICANT VARIABLES FOR TRADING STRATEGIES.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 330-335

DOI: 10.5220/0002354203300335

 SciTePress

1.2 Investment Strategies

An investment strategy is a behaviour routine

devised by investors to enable them to make

decisions in view of the different situations which

may arise. This basically entails following a fixed

strategy over a period of time, while in technical

terms, it is a predefined set of rules to be applied.

Strategies are normally based on

micro/macroeconomic data, on statistical indicators,

or on technical analysis of the historical evolution of

the share price. Investment strategies receive share

prices in real time and include trading orders which

are automatically executed in the market. Investors

use investment strategies as tools to help in the

decision-making process and to eliminate the

emotional factor which an investment involves.

The strategy operates by using various

parameters defined by the user and which have been

adjusted from historical analysis and studies of the

real market.

There are strategies which are ideal in certain

circumstances but which fail where others triumph.

Therefore, the choice of the ideal strategy to apply in

the immediate unknown future is a very difficult

task. In order to know the true potential of a strategy

it is necessary to calibrate a multitude of factors

which affect its behaviour as we shall see in the

following sections.

A variety of procedures can also be found in the

literature for evaluating and recommending

strategies. Fung and Hsieh (Fung and Hsieh, 1997),

for example, classify the strategies empirically

according to their behaviour into the following 5

groups: “Systems / Trend-following”, “Systems /

Opportunistic”, “Global / Macro”, “Value”, and

“Distressed”. Schittenkopf’s work (Schittenkopf,

2000) is similar in some ways to that presented here

in that it analyzes the relationship between volatility

and profit variables, although it only analyses a

single investment strategy on a single stock market

index. Our work, on the other hand, attempts to be

more general by analyzing a set of variables, for a

series of strategies, on a wide range of stock market

prices.

In the second section of this article, we will

describe the strategies used, and how they may be

optimized and evaluated. Section 3 analyzes the

selected variables and explains why they were

chosen. We will end the article with our conclusions

and future lines of research.

2 METHODOLOGY

The first step in our study was to obtain a series of

investment strategies and also the parameters for

each strategy with their respective levels. For that

we will use the records from Gaesco Bolsa.

Gaesco Bolsa S.A., one of the largest capital

management companies in Spain, is constantly

analysing automatic stock market investment

strategies. We were given access to the 500 best

strategies. While some come from their R&D

department, others come from specialist journals

(Stocks & Commodities, Trader) and others are

proposed by their own clients. Each strategy is

studied on a wide battery of scenarios by means of a

demanding and exhaustive procedure which only a

few strategies survive.

When the investment strategy is not based on

human decisions, it can be simulated in time by what

is known as an automatic system. A simulation is an

execution of a strategy on a stock market index over

a period of time.

In order to simplify our explanation as far as

possible, we will present an example of a basic

investment strategy, consisting of three behaviour

rules:

Entry rule:

 Purchase if the current share price exceeds the

maximum of the last N days

Exit rules:

 Sell if an X% profit is obtained on the entry

point

 Sell if a Y% loss is obtained in relation to the

entry point

The underlying philosophy behind this strategy

tells us that the fact of exceeding the maximum

(frequently called resistance) in the last N days is

normally an indication of the start of an upward

movement. We will sell after earning a certain

amount of profit, although we will make sure that

we do not lose more than a certain limit. This

strategy has three adjustable parameters:

 N: number of days which are considered in the

calculation of the entry point

 X: percentage of profits required before

liquidating positions

 Y: maximum percentage loss permitted

The code for the strategy implemented by means

of Visual Basic to be used directly on the Visual

Chart platform would be:

'¡¡ Parameters

Dim N As Integer

Dim X As Double

Dim Y As Double

'Parameters !!

Public Sub OnCalculateBar(ByVal Bar As Long)

AN EMPIRICAL STUDY OF SIGNIFICANT VARIABLES FOR TRADING STRATEGIES

331

With APP

Dim Resistance As Double

Dim Benefit As Double

Dim Loss As Double

Resistance=.GetHighest(PriceHigh, N)

.Buy AtStop, 1, Resistance

Benefit=.GetEntryPrice+(.GetEntryPrice*X/100)

Loss=.GetEntryPrice-(.GetEntryPrice*Y/100)

.ExitLong AtLimit, 1, Benefit

.ExitLong AtStop, 1, Loss

End With

End Sub

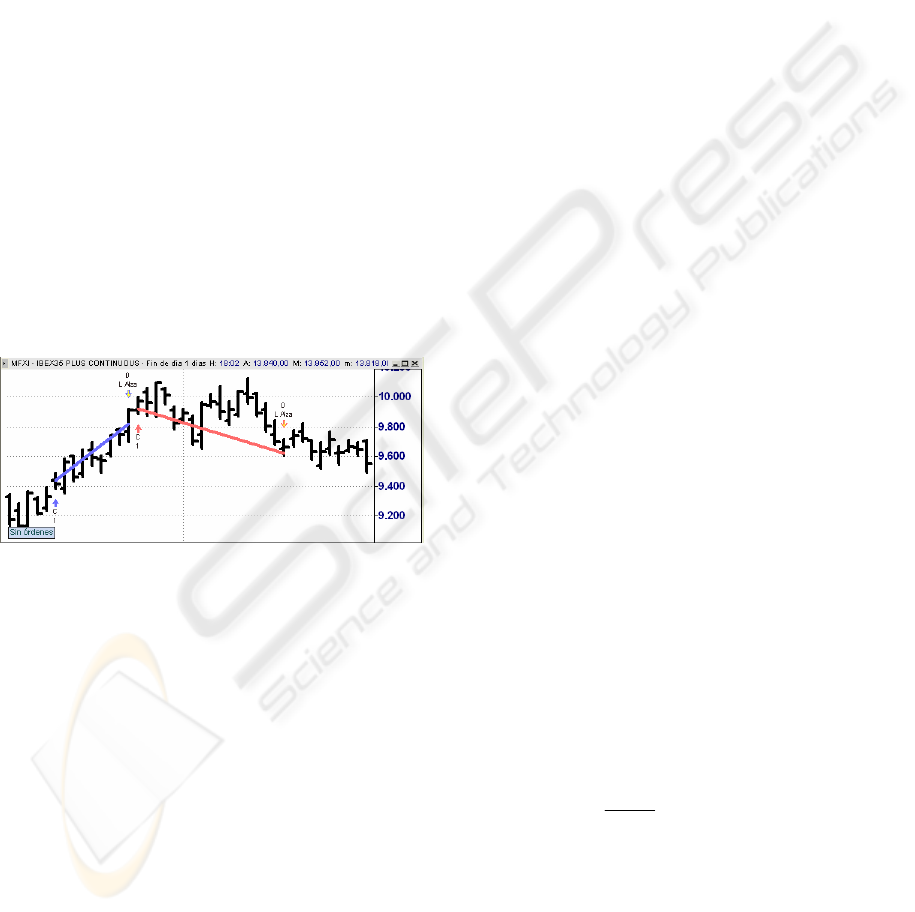
This strategy on the Nasdaq-100, establishing the

values N=5, X=4, Y=3 as parameters, is shown in

Figure 1. Each vertical bar determines the range of

values covered during a day’s trading. The small

horizontal bar on the left-hand side represents the

initial value of the day and the small right-hand bar

the final value. Two trades can be observed. A trade

is defined as the fact that it starts when a value/good

is purchased and ends when it is sold. The first trade

is positive, since it is purchased at 9440 and sold at

9818, a result of +4%. The second trade, meanwhile,

is negative since it is purchased at 9919 and sold at

9621, a result of -3%. The line which joins the entry

point and the exit point of a trade is a visual tool

which enables the strategy to be monitored.

Figure 1: Example of a strategy’s performance.

Taking the session closing price of each trading

day as a reference, and knowing the entry and exit

points of the investment strategy, it is possible to

calculate a strategy’s daily percentage profit. This

leads to a time series of daily profits which will be

used in the following stages of our study.

2.1 Genetic Optimization of Strategies

A typical strategy has several adjustable parameters

(permitted tolerance, reaction speed, profit, loss,

etc.). Each parameter is defined with the following

quadruple: [name, minimum value, maximum value,

scale]. For example, our previously presented

strategy comprises three parameters:

 [Days, 0, 250, 1]

 [Profit, 0, 250, 0.1]

 [Loss, 0, 100, 0.1]

The previous example would give us a set of

250,000,000 possible combinations of parameters,

making impossible to analyse and evaluate all of

them. We are interested in optimising a strategy’s

parameters and searching for those which produce

the best performance. For that we resort to a genetic

algorithm (Holland, 1975; Goldberg, 1989) which

enables us to obtain an acceptable combination in a

feasible period of time. In the following section, we

will briefly describe the genetic algorithm used.

2.1.1 Definition of the Individual

Each individual in the population corresponds to a

certain combination of parameters and the associated

chromosome is the binary codification of that

combination. From each parameter’s range, it is

possible to obtain the number of bits necessary for

its codification. Certain ranges require pre-

processing prior to codification:

1) If the range starts at a value other than 0, a value

will be added or subtracted to move the start of the

range to 0.

2) If the range includes decimal values, these will be

multiplied by 10 until they become integer values.

In order to code a chromosome in our example

strategy, 32 bits would therefore be necessary:

 [Days, 0, 250, 1] needs 8 bits.

 [Profit, 0, 100, 0.1] needs 12 bits.

 [Loss, 0, 100, 0.1] needs 12 bits.

The combination – 36, 1.5, 2.5 – will be coded:

00100100 000000001111 000000011001

2.1.2 Fitness Function of the Individual

Each individual in the population has an associated

fitness value. For our problem, an individual’s

fitness is the performance obtained when the

strategy is applied on a certain index with the set of

parameters represented in its chromosome. As a

result of this simulation, a series of trades is

obtained. The fitness is equal to the sum of the

percentage profits of each trade once administration

expenses and commissions have been deducted:

∑

−

Commission

)(

(1)

where N is the total number of trades, I is the

purchase price, and O is the sale price.

2.1.3 Crossover Operator

We will pair two individuals from the population in

order to generate two new individuals, and we have

ICEIS 2007 - International Conference on Enterprise Information Systems

332

applied the crossover operator on 1 point (see Figure

2). This operator takes 2 parents from the

population, pairs them and obtains 2 children. To do

so, it randomly chooses a crossover point which

divides the father’s and mother’s chromosomes into

two halves. The first child is formed with the first

half of the father and the second half of the mother,

and the second child with the first half of the mother

and the second half of the father.

Figure 2: One point crossover.

2.1.4 Mutation Operator

The chromosome is taken and is mutated by

randomly changing some of its bits. It is necessary

to bear in mind that after the cross or mutation

operation, the descendants might not be valid

population individuals, and it might therefore be

necessary to repeat the process until the desired

number of individuals is obtained.

2.2 Evaluation Method

Many investors design their investment strategies,

optimise their parameters, and apply them to the real

world, trusting the optimisation results. In the

majority of cases, these strategies inevitably fail and

fail dismally. The reason for this failure is very

simple: they fail because while the strategy has

learned to behave excellently in a specific period of

time, it has not been able to generalise its parameters

to act in a different period.

In our study, once the investment strategies have

been calibrated, they are evaluated by means of a

blind test on different periods of time to those used

in optimisation in order to carry out as realistic a

simulation as possible. The subsequent evaluation of

the investment strategy will not take into account the

results obtained in optimisation, but will only work

with the test results.

An evaluation method has been followed based

on the sliding window technique to carry out the set

of optimisations-tests.

As genetic algorithms are probabilistic methods,

the results of a simple execution can be inadequate.

In order to avoid this as far as possible, the

evaluation method is repeated 5 times, and a series

of daily profits is obtained from each iteration. The

final series used to calculate the variables will be the

average of the 5 previous series.

The number of iterations of the genetic algorithm

varies according to the strategy. As is logical, the

strategies with the greatest number of parameters

require a greater number of iterations. By default,

the number of iterations is fixed to a tenth of the

number of possible combinations.

Following the evaluation method described in

this section, the 500 available strategies were

evaluated on six stock market indexes: four

European ones (CAC-40, DAX-30, IBEX-35 and

EUREX-50) and two American ones (NASDAQ-

100 and RUSSELL-1000). We obtained a database

of 3000 entries on which we will extract the

significant variables.

3 OBTAINING SIGNIFICANT

VARIABLES

Once the strategy has been perfectly calibrated, we

can proceed to extract the variables which

characterise its behaviour. As we have already

mentioned, the result of the previous tests is a set of

3000 daily profit time series. The profits are

expressed in terms of percentages and perfectly

match reality, i.e. they take into account the

commissions of the different national stock markets

and of their respective brokers, and also the

slippages which occur when entering or exiting a

trade.

Since almost every agent uses his/her own

descriptive variables about a strategy’s behaviour,

there might currently be thousands of operative

variables. We, meanwhile, are looking for a series of

significant variables which cover all aspects of a

strategy’s behaviour and which describe it

univocally.

After studying the semantics of hundreds of

variables, we reached the conclusion that they could

be grouped into four categories. The first and largest

of these covers performance-related variables:

absolute profit, percentage profit, annualised profits,

Sharpe ratio, Sortino ratio, Treynor ratio, swing,

capital asset pricing model (CAPM), etc. The second

group contains the variables which, in some way,

measure the risk, such as for example volatility, loss

series, consistency, monthly risk, risk-adjusted

return, risk-free return, alpha, systematic risk (beta),

Jensen’s measure, etc. The third group consists of

the variables associated with trading. Variables

belonging to this group would be: activity,

reliability, average profit per trade, average profit

per positive trade, average profit per negative trade,

etc. Finally, the fourth group comprises variables

AN EMPIRICAL STUDY OF SIGNIFICANT VARIABLES FOR TRADING STRATEGIES

333

which globally measure the quality of a strategy in

comparison with the remaining strategies. Basically,

this consists in ranking the strategies according to a

series of criteria and allocating 5 stars to the best

strategies, 4 stars to the next ones, and so on. The

strategies with 1 star are those with the worst

assessment.

We have detected that many variables are

equivalent to each other or simply change scale or

nomenclature. In collaboration with the experts, the

authors have extracted a series of significant

variables which describe how good the strategies

are. After our initial selection, the most indicative

and suitable variables are selected on the basis of the

results of a survey carried out among experts. From

each times series, a group of numerical variables is

extracted which will help us to describe a strategy’s

behaviour:

Profit: This annualised performance takes into

account commissions and slippages:

yearsRG

∑

(2)

where R

is a strategy’s performance in percentage

terms.

Volatility: Volatility is the standard deviation of the

change in the value of a financial instrument with a

specific time horizon. It is frequently used to

quantify the risk of the instrument during this time

period. Volatility is expressed in annualised terms.

The annualised volatility σ is proportional to the

standard deviation σSD of the returns of the

instrument divided by the square root of the time

period of the returns:

σσ

(3)

where P is the period of the returns in years.

Loss series (Drawdown): this is the greatest loss

sequence, or rather, the greatest drop between the

peak of accumulated profit and the lowest point.

Measurement begins when the fall starts and ends

when a new maximum is reached, since the lowest

point is not known until a new maximum is reached.

More formally, if X(t) gives the accumulated profit

at a moment in time t, the loss series at a moment T

would be:

[]

)()(,0

0,0)0(

),0(

tXMaxtXMinDD

Tt∈

−−=

≥=

(4)

Sharpe ratio: the Sharpe ratio is a measure of risk-

adjusted performance of an investment asset, or a

trading strategy, and is defined as:

/GS

(5)

where G is the strategy return and

is the volatility

of the strategy return. The Sharpe ratio is used to

characterize how well the return of an asset

compensates the investor for the risk taken.

Potential: this is a measurement of the performance

in relation to the maximum loss series:

DDGP /

(6)

Consistency: in general terms, the consistency refers

to the property of maintaining the same form over

time. In our case in particular, it indicates the

frequency of negative results over time:

)0,(

∑

RRSD

(7)

where SD is the standard deviation of the negative

return values.

Reliability: this is the number of winning trades

expressed as a percentage of the total number of

trades:

100*/_ tradestradeswinningF

(8)

E01: one-year stars following Standard & Poors’

method. By dividing the strategy's average relative

performance by the volatility of its relative

performance, we are measuring not only its ability to

outperform its peers but also to do so in a consistent

way; the higher the ratio, the greater the strategy's

ability to outperform its peers consistently.

volatilityrelativereturnrelativeRR _/_

(9)

Let us suppose we have 100 strategies, then the

strategy stars will be:

 5 stars: top 10%, 10 strategies

 4 stars: top 11-30%, 20 strategies

 3 stars: top 31-50%, 20 strategies

 2 stars: next 25%, 25 strategies

 1 star: bottom 25%, 25 strategies.

E04: we follow the same procedure as the one-year

stars (E01), but considering four years.

Number of Trades (Activity): this is the number of

entries-exits per day.

daystradesA /##

(10)

ICEIS 2007 - International Conference on Enterprise Information Systems

334

4 CONCLUSIONS AND FUTURE

WORK

One interesting conclusion was obtained from the

optimization process, and this is that the most

elaborate and complex strategies, and therefore those

with the greatest number of parameters, obtained

excellent values in optimisation but disastrous ones

in the test. On the other hand, while more basic and

simpler strategies with a lower number of

parameters did not perform particularly well in

optimisation they did in tests. This is due to the fact

that very complex strategies are capable of perfectly

adjusting to the particular characteristics of the

optimisation period, but overlearn and do not know

how to act when the conditions change. However,

simpler strategies abstract and generalise better and

their behaviour is similar in both optimisation and

test periods.

The extracted data are extremely valuable since

they can be used to carry out a large number of

scientific studies. A first study would consist in

representing the previous data in a data warehouse

and applying different data mining techniques in

order to extract patterns between the different

variables. Taking into account that the values of the

variables can easily be transformed into fuzzy

variables by means of linguistic labels, it would be

possible to carry out a similar study to the previous

one by using a fuzzy data warehouse capable of

extracting fuzzy association rules (Delgado, 2007).

Similarly, it would be advisable to find the results

with the greatest significant interest (Shekar, 2004).

The portfolio selection problem (Schlottmann

2004) can also be studied by using the methodology

in this work. This problem consists in looking for

the combination of strategies which, by acting

jointly, increase profits and reduce risk. This is a

typical multiobjective optimisation problem. The

data can also be studied with clustering techniques

which search for the groupings between strategies or

variables.

It would also be interesting to devise an expert

system for stock market investment, and one

possibility might be to achieve an expert assessment

of each strategy. By applying neural networks or

some other artificial intelligence technique, expert

knowledge could then be abstracted and represented

for implementation on the expert system’s

knowledge base.

The information obtained is subject to changes

according to time. An analysis could be carried out

to search for values which have undergone changes,

thereby obtaining new knowledge and eliminating

part of the previous knowledge (Chen, 2005).

REFERENCES

Baba, N., Inoue, N. et al, 2002. Utilization of Soft

Computing Techniques for Constructing Reliable

Decision Support Systems for Dealing Stocks. In

IJCNN’02: Proceedings of the 2002 International

Joint Conference on Neural Networks, Honolulu,

Hawaii.

Chapman, A.J., 1994. Stock Market Trading Systems

Through Neural Networks: Developing a Model.

International Journal of Applied Expert Systems, Vol.

2, no. 2, 1994, pages 88-100.

Chen, M., Chiu, A., Chang, H., 2005. Mining changes in

customer behaviour in retail marketing. Expert

Systems with Applications, 28, 773-781.

Delgado Calvo-Flores, M., Gibaja Galindo, E., Molina

Fernández, C., Nuñez Negrillo, J., 2007. Using Fuzzy

DataCubes in the Study of Trading Strategies. ICEIS

2007: International Conference on Enterprise

Information Systems, Funchal, Madeira – Portugal.

Fung, W., Hsieh, D., 1997. Empirical characteristics of

dynamic trading strategies: The case of hedge funds.

Review of Financial Studies, 10, 275-302.

Goldberg, D.E., 1989. Genetic Algorithms in Search,

Optimization, and Machine Learning. Addison-

Wesley. New York, USA.

Holland, J.H., 1975. Adaptation in Natural and Artificial

Systems. Ann Arbor, MI/USA: Mich. Univ. Press.

Liu, N. K., Lee, K. K., 1997. An Intelligent Business

Advisor System for Stock Investment. Expert Systems

14(3): 129-139.

Schittenkopf, C., Tino, P., Dorffner, G., 2000. The

profitability of trading volatility using real-valued and

symbolic models. In IEEE/IAFE/INFORMS 2000

Conference on Computational Intelligence for

Financial Engineering, New York City, NY, pages 8–

11.

Schlottmann, F., Seese, D., 2004. Financial applications of

multiobjective evolutionary algorithms: recent

developments and future research directions. In

Coello-Coello, C.; Lamont, G. (eds.): Applications of

Multi-Objective Evolutionary Algorithms, World

Scientific, Singapore, pages 627-652.

Shekar, B., Natarajan, R., 2004. A Framework for

Evaluating Knowledge-Based Interestingness of

Association Rules. Fuzzy Optimization and Decision

Making 3, 157-185.

Skabar, A., Cloete, I., 2001. Discovery of Financial

Trading Rules. Proceedings of the IASTED

International Conference on Artificial Intelligence and

Applications.

AN EMPIRICAL STUDY OF SIGNIFICANT VARIABLES FOR TRADING STRATEGIES

335